Investigating the impact of exit effects on solute transport in macroporous media

The effect of macropore flow on solute transport has spurred much research over the last forty years. In this study, non-reactive solute transport in water-saturated columns filled with porous media crossed by a macropore was experimentally and numerically investigated. The emphasis was put on the study of exit effects, whose very existence is inherent to the finite size of any experimental column. We specifically investigated the impact of a filter at the column outlet on water flow and solute transport in macroporous systems. Experiments involving breakthrough measurements and magnetic resonance imaging (MRI) showed that solute transport displayed some significant non-unidirectional features, with a strong mass exchange at the interface between the macropore and the matrix. Fluid dynamics and transport simulations indicated that this was due to the non-unidirectional nature of the flow field close to the outlet filter. The flow near the exit of the column was shown to be strongly impacted by the presence of the outlet filter, which acts as a barrier and redistributes water from the macropore to the matrix. This impact was apparent on the breakthrough curves and the MRI images. It was also confirmed by computer simulations and could, if not properly taken into account, impede the accurate inference of the transport properties of macroporous media from breakthrough experiments.

1 Introduction

Column experiments are frequently performed to study the transport of various contaminants in soils (De Matos et al., 2001; Pang et al., 2002; Banzhaf and Hebig, 2016; Jin et al., 2000) or to fit experimental data with a transport model (Nielsen and Biggar, 1961; De Smedt and Wierenga, 1984; Cortis and Berkowitz, 2004). The general motivation shared by all these experiments is to study and to understand the transport processes occurring in the bulk of a porous medium in a simple and reproducible setting by imposing a stationary flow along the axis of the column.

Experimentally, this task is more challenging than it might appear at first sight. The finite size of the column can impact water flow and solute transport with, for instance, the existence of entrance–exit effects affecting the uniformity of the flow near the extremities of a column (Koestel and Larsbo, 2014; Flury et al., 1999; Starr and Parlange, 1977; Bromly et al., 2007). Similar issues have been underlined in chromatography (Guiochon, 2006; Farkas et al., 1994; Baur et al., 1988; Farkas et al., 1997; Shalliker et al., 2000; Broyles et al., 1999; Gritti and Gilar, 2019) and in some fundamental studies of transport in porous media (Lehoux et al., 2016; Deurer et al., 2004; Greiner et al., 1997). The perturbations induced by the entrance and the exit ends of the column can have a concrete incidence (e.g. flow disturbance and recirculation in the system reservoirs, additional solute dispersion). Consequently, the breakthrough curves (BTCs) may be affected by entrance–exit effects and may no longer reflect the intrinsic transport properties of the porous medium, but the transport properties of the whole experimental system (Lehoux et al., 2016; Schwartz et al., 1999; Starr and Parlange, 1977; James and Rubin, 1972). Several parts of the column device can impact the solute breakthrough (Giddings, 2002): upstream and downstream reservoirs, restrictions between the reservoirs and the tubes, and frits or filters positioned at the inlet and outlet. These inert physical filtration devices are often employed to diffuse the incoming water flow evenly on the entrance face of the porous medium and to prevent porous medium particles from exiting and clogging the tubes downstream.

All these parts, located right before and/or right after the porous medium, may trigger water flow and solute transport disturbances, especially when the porous medium under scrutiny is heterogeneous (Barry, 2009). Heterogeneous columns have in particular been employed in transport studies motivated by questions raised by the complexity of water infiltration and mass transport in soils. Soils frequently contain macropores (Beven and Germann, 2013), which are large and continuous openings known to be involved in the rapid displacement of water and chemical substances. Various breakthrough experiments have been performed to study the role played by single macropores embedded in a porous medium (Allaire et al., 2009). However, unsaturated conditions are difficult to sustain in a well-controlled fashion and the effect of macropores on transport culminates when they are water saturated. Thus, many results have been obtained from macroporous columns operated in the saturated regime, with different artificial systems: packed soils containing constructed macropores, macroporous sandy media, glass bead packings crossed by a macropore, etc. (Allaire et al., 2009; Li and Ghodrati, 1997; Ghodrati et al., 1999; Lamy et al., 2009; Batany et al., 2019). The impact of entrance–exit effects has been noticed in a few studies (Flury et al., 1999; Kreft and Zuber, 1978), but to our knowledge, the underlying mechanisms responsible for these effects have never been thoroughly investigated.

This paper aims to demonstrate the significant influence of an outlet filter on water flow and non-reactive solute transport within an artificial macroporous system (the inlet filter was always set in place to prevent any clogging of the macropore). Using a combination of breakthrough experiments, MRI monitoring and computer simulations, we show that water flow and non-reactive solute transport in water-saturated macroporous media are strongly affected by the presence of a filter at the end of the column. This filter influences the velocity field in a sizable fraction of the macroporous medium and strongly impacts the transport of solute in the system and its elution at the outlet.

2 Materials and methods

2.1 Porous media and columns

Several experimental columns filled with Hostun sand (HN 0.6/1.6, Sibelco, France) were constructed. Before any experiment, the sand was sieved at 0.5 mm with a stainless mesh sieve. The sand was first washed with a 2 mol L⁻¹ nitric acid solution obtained by diluting nitric acid 65 % (Emsure, Millipore) in ultrapure water (Milli-Q Integral 3 Water Purification System, Millipore). The sand was then rinsed twice with ultrapure water and neutralized with a 0.1 mol L⁻¹ potassium hydroxide solution obtained by diluting 1 mol L⁻¹ potassium hydroxide (Titripur, Millipore) in ultrapure water. Afterward, the sand was rinsed several times with ultrapure water until the pH of the solution reached the pH of the rinsing solution. Finally, the sand was dried at 105 ^∘C for 24 h and then stored in a plastic container. The particle size distribution of the sand was measured by laser diffraction (Mastersizer 3000, Malvern). It ranged between 0.30 and 1.10 mm, with a median particle diameter equal to 1.0 mm.

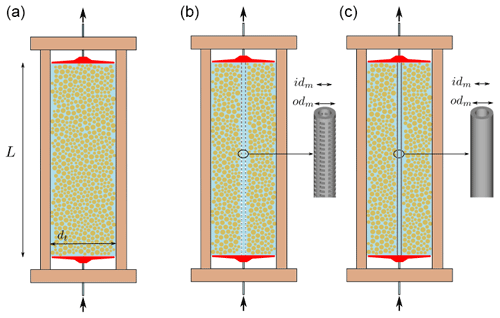
Two hollow cylinders were used as macropores. They were 3D printed (Form 1+, Formlabs) using a photoreactive resin (Clear Resin, Formlabs), with a 0.1 mm spatial resolution. The hollow cylinders had an inner diameter id_m=3.0 mm, an outer diameter od_m=5.0 mm and a height of 15.0 cm. The first hollow cylinder was plain (no holes), whereas the second one was perforated with 0.5 mm diameter holes resulting in a 25 % surface porosity. These two hollow cylinders were used to model impermeable and permeable macropores, respectively. Water could flow and solute could cross the boundaries of the perforated hollow cylinder, whereas the plain one was impermeable to water flow and solute transfer.

We used XK 50/30 (Cytiva) columns to pack the porous media. The inner diameter of each column was equal to d_col=5.0 cm and their height was equal to L=15.0 cm. The macroporous columns were set up by inserting the hollow cylinders along the axis of the columns. Then, the Hostun sand was slowly poured around and dry packed using gentle manual vibrations. Once filled with sand, each column was saturated over 2 h with carbon dioxide, a gas much more soluble in water than air. The column was then slowly water saturated with a conditioning solution. Then, it was rinsed with 12 pore volumes of the same conditioning solution at different flow rates (from 0.5 to 3.0 mL min⁻¹) to stabilize the pH and the electrical conductivity.

Mesh filters (Net Rings, Cytiva) adapted to the XK 50/30 columns with 10 µm pores were positioned just before and right after the porous medium. The exit effect, which is the focus of this study, was studied by removing the outlet filter for some experiments.

Three experimental columns (denoted A, B and C) were prepared according to the aforementioned methodology: column A is a homogeneous control column without any macropore, column B contains a perforated hollow cylinder along its axis acting as a permeable macropore and column C contains a plain hollow cylinder along its axis acting as an impermeable macropore. The columns are depicted in Fig. 1. The pore volume of each column was estimated by weighing the column before and after saturation. The values were 119.5, 116.6 and 120.2 mL for columns A, B and C, respectively.

Figure 1 Columns used for the injection of solutes: homogeneous control column A (a), macroporous columns with the perforated hollow cylinder B (b) and the plain hollow cylinder C (c). The liquid distribution and collection systems are drawn in red.

2.2 Aqueous solutions

We used two conditioning solutions and two tracer solutions. A $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}{\mathrm{mol}\mathrm{L}}^{-\mathrm{1}}$ potassium nitrate (KNO₃) solution was used as the first conditioning solution. The first tracer solution was a $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{2}}{\mathrm{mol}\mathrm{L}}^{-\mathrm{1}}$ potassium nitrate solution. Both solutions were prepared by dissolving solid potassium nitrate (Emsure, Millipore) in ultrapure water. The conditioning and tracer solutions had an electrical conductivity of ${\mathit{\sigma }}_{\mathrm{0}}=\mathrm{0.01}{\mathrm{mS}\mathrm{cm}}^{-\mathrm{1}}$ and ${\mathit{\sigma }}_{\mathrm{1}}=\mathrm{1.19}{\mathrm{mS}\mathrm{cm}}^{-\mathrm{1}}$, respectively. These solutions were used for the determination of the BTCs.

The second conditioning and tracer solutions were prepared by dissolving gadolinium(III) chloride hexahydrate (Sigma-Aldrich) in ultrapure water. The second conditioning solution was a $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{4}}{\mathrm{mol}\mathrm{L}}^{-\mathrm{1}}$ GdCl₃ solution (electrical conductivity ${\mathit{\sigma }}_{\mathrm{0}}=\mathrm{0.03}{\mathrm{mS}\mathrm{cm}}^{-\mathrm{1}}$) and the second tracer solution was a $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{2}}{\mathrm{mol}\mathrm{L}}^{-\mathrm{1}}$ GdCl₃ solution (${\mathit{\sigma }}_{\mathrm{1}}=\mathrm{2.86}{\mathrm{mS}\mathrm{cm}}^{-\mathrm{1}}$). We used these solutions for visualizing Gd³⁺ transport within the column by MRI (see Sect. 2.4). Complementary BTCs were also measured with this second set of solutions.

All solutes were considered to behave as conservative tracers, i.e. non-reactive chemical species following the water flow without any sorption, neither to the particles of the porous media nor to the walls of the hollow cylinder.

2.3 Breakthrough experiments

Columns were arranged in an upright position and solutions were injected from the bottom to the top using a peristaltic pump (Ismatec ISM834A) connected to the injection system of a ÄKTAprime device (Cytiva) with polyether ether ketone (PEEK) tubing having a 0.75 mm inner diameter (Cytiva) and capillary tubing with an inner diameter of 1.55 mm included in the adapters of the XK 50/30 column. This low-pressure liquid chromatography system was used to continuously monitor electrical conductivity, pH, UV absorbance and temperature at the outlet of the column.

Each breakthrough experiment began with the injection of more than two pore volumes of conditioning solution to stabilize the pH and the electrical conductivity measured at the outlet of the column. Then, 5 mL of tracer solution was injected. The flow rate was set to $Q=\mathrm{3}{\mathrm{mL}\min }^{-\mathrm{1}}$, corresponding to a mean Darcy velocity $q=\mathrm{4}Q/\left(\mathit{\pi }{d}_{\mathrm{col}}^{\mathrm{2}}\right)$ equal to 0.15 cm min⁻¹. Each breakthrough experiment was triplicated. The relative concentration was determined from the measurement of the electrical conductivity σ at the outlet as follows:

$$\begin{array}{}\text{(1)}& C={\displaystyle \frac{\mathit{\sigma }-{\mathit{\sigma }}_{\min }}{{\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\min }}},\end{array}$$

where σ_min stands for the minimum electrical conductivity obtained when the conditioning solution is injected and σ₁ is the electrical conductivity of the tracer solution.

Figure 2 MRI sequence employed for image acquisition.

2.4 Magnetic resonance imaging

The transport of Gd³⁺ within a column, which is an opaque three-dimensional system, was monitored with a vertical nuclear magnetic resonance spectrometer (DBX 24/80 Bruker), operating with a 0.5 T static magnetic field (20 MHz ¹H frequency) and equipped with a birdcage radio-frequency coil delimiting a measurement zone of 20 cm in diameter and 20 cm in height. Due to its paramagnetic properties, Gd³⁺ is an excellent MRI contrasting agent (Pyykkö, 2015) and has already been used to study solute transport in soils (Haber-Pohlmeier et al., 2017).

As for the breakthrough experiments, the Gd³⁺ solution was injected at 3.0 mL min⁻¹ in the column from the bottom with a peristaltic pump connected to the ÄKTAprime device. The sole difference between the classical and the MRI-monitored breakthrough experiments was that in the latter case, the connecting tubes were longer (10 m before the entrance and 10 m after the exit of the column), so that the injection system was outside the MRI setup.

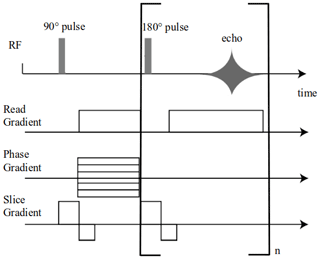
Two-dimensional MRI vertical slices of 6 mm thickness encompassing the axis of the column were taken at different times during the injection of the solute. Each image had 128×64 pixels and was acquired in 3 min 55 s. The field of view was 19 cm×5.5 cm, providing a spatial resolution of $\mathrm{1.48}{\mathrm{mm}\mathrm{pixel}}^{-\mathrm{1}}\times \mathrm{0.85}{\mathrm{mm}\mathrm{pixel}}^{-\mathrm{1}}$. A multi-spin multi-echo (MSME) sequence, schematized in Fig. 2, based on a succession of 16 echoes was used with an echo time T_E=7.4 ms and a recycle delay T_R=1.2 s. To produce a two-dimensional image, the measured 16 echoes were added in order to improve the signal-to-noise ratio without increasing the measurement time (Zhou et al., 2019), thus preventing direct concentration quantification. Moreover, due to the short recycle delay used to keep the measurement time below 4 min, the resulting signal depends simultaneously on the spin–lattice relaxation time T₁ and the spin–spin relaxation time T₂, thus complicating quantification. The MRI images can nevertheless be used to evaluate where Gd³⁺ is present within the column.

2.5 Computer simulations

Numerical simulations were performed with COMSOL Multiphysics (version 5.4), a commercial finite element software. COMSOL Multiphysics was used to define the geometry of the problem, to generate the computational mesh and to solve the partial differential equations governing the fluid flow and the non-reactive transport of the solute, with the specified initial and boundary conditions.

To simulate column B, we developed a two-dimensional axisymmetric geometric model (15.0 cm length and 2.5 cm radius) with two regions: one for the sandy matrix and another for the macropore. The filters were represented as 10 µm thick porous media. The geometry of the inlet and outlet reservoirs was also taken into account in the numerical model.

The mesh was automatically built by COMSOL Multiphysics. It was adapted to the geometry previously defined with an increase in node density at the interfaces between subdomains and in small subdomains (like the filters and the reservoirs). We checked that the numerical results remained unaffected when the mesh was refined.

The stationary flow of the carrier liquid within the column was described by the Stokes equations in the macropore (free region) and by the Brinkman equations in the surrounding porous medium (Guyon et al., 2015). The Stokes equations read

$$\begin{array}{}\text{(2)}& \left\{\begin{array}{l}-\mathrm{\nabla }(p-\mathit{\rho }gz)+\mathit{\mu }△u=\mathrm{0}\\ \mathrm{\nabla }\cdot u=\mathrm{0}\end{array}\right.,\end{array}$$

where p stands for the liquid pressure, μ for the dynamic viscosity of the liquid, g for the gravitational acceleration, ρ for the liquid density, z for the vertical coordinate and u for the velocity field of the liquid.

In the surrounding porous medium and the filters, the Brinkman equations were used to model the liquid flow since momentum transport induced by shear stresses is of importance at the interface between the macropore and the porous matrix (Ochoa-Tapia and Whitaker, 1995). These equations extend Darcy's law to describe the dissipation of kinetic energy by viscous shear and read

$$\begin{array}{}\text{(3)}& \left\{\begin{array}{l}-\mathrm{\nabla }(p-\mathit{\rho }gz)+\mathit{\mu }{\mathit{\varphi }}^{-\mathrm{1}}△u-\mathit{\mu }{\mathit{\kappa }}^{-\mathrm{1}}u=\mathrm{0}\\ \mathrm{\nabla }\cdot u=\mathrm{0}\end{array}\right.,\end{array}$$

where ϕ is the porosity and κ the permeability of the porous matrix.

The non-reactive solute transport was modelled by the advection–diffusion equation in the macropore and the advection–dispersion equation in the porous medium. Both equations can be written as

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\partial c}{\partial t}}=\mathrm{\nabla }\cdot (\underset{\mathrm{¯}}{\underset{\mathrm{¯}}{D}}\cdot \mathrm{\nabla }c)-u\cdot \mathrm{\nabla }c.\end{array}$$

In the macropore, $\underset{\mathrm{¯}}{\underset{\mathrm{¯}}{D}}$ denotes the isotropic tensor $D_{\mathrm{0}}\underset{\mathrm{¯}}{\underset{\mathrm{¯}}{I}}$, D₀ being the molecular diffusion coefficient of the solute and $\underset{\mathrm{¯}}{\underset{\mathrm{¯}}{I}}$ the second-order identity tensor. In the porous matrix and the filters, $\underset{\mathrm{¯}}{\underset{\mathrm{¯}}{D}}$ denotes the transversely isotropic tensor $D_{\mathrm{L}}\widehat{u}\otimes \widehat{u}+D_{\mathrm{T}}(\underset{\mathrm{¯}}{\underset{\mathrm{¯}}{I}}-\widehat{u}\otimes \widehat{u})$, where D_L is the longitudinal coefficient of dispersion, D_T the transverse coefficient of dispersion and $\widehat{u}\equiv u/\left|u\right|$ the normalized vector parallel to the water flux. The symbol ⊗ denotes the tensor product. In the porous matrix, D_L and D_T combine the effects of both molecular diffusion and mechanical dispersion and can be written as follows (Bear, 1988):

$$\begin{array}{}\text{(5)}& \left\{\begin{array}{l}{D}_{\mathrm{L}}={\mathit{\lambda }}_{\mathrm{L}}\left|u\right|+\mathit{\tau }{D}_{\mathrm{0}}\\ D_{\mathrm{T}}={\mathit{\lambda }}_{\mathrm{T}}\left|u\right|+\mathit{\tau }{D}_{\mathrm{0}}\end{array}\right.,\end{array}$$

where τ is the tortuosity of the porous medium, λ_L the longitudinal dispersivity and λ_T the transverse dispersivity. Moreover, we assumed for the sake of simplicity that the transverse dispersivity was equal to one-tenth of the longitudinal dispersivity, ${\mathit{\lambda }}_{\mathrm{T}}=\frac{\mathrm{1}}{\mathrm{10}}{\mathit{\lambda }}_{\mathrm{L}}$ (Zech et al., 2018).

Solving Eqs. (2), (3) and (4) requires knowledge of the hydraulic and transport properties of the porous medium and the filters. Regarding hydraulic properties, by considering sand grains as spheres, the permeability of the sand was evaluated with the Kozeny–Carman equation (Guyon et al., 2015),

$$\begin{array}{}\text{(6)}& \mathit{\kappa }={\displaystyle \frac{{\mathit{\varphi }}^{\mathrm{3}}{d}_{\mathrm{g}}^{\mathrm{2}}}{\mathrm{180}{\left(\mathrm{1}-\mathit{\varphi }\right)}^{\mathrm{2}}}},\end{array}$$

with d_g being the mean diameter of the grains. In order to fit the experimental BTCs, d_g was taken to be equal to 0.57 mm, yielding for the sand a permeability of $\mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{10}}{\mathrm{m}}^{\mathrm{2}}$. The filter was modelled as a thin porous slab periodically perforated by square holes of side length a=10 µm. The surface porosity of the slab has been taken to be equal to ϕ_filter=25 %. According to Bruus (2007), for a laminar flow, the permeability of a single channel with a square cross section of side length a is equal to

$$\begin{array}{}\text{(7)}& {\mathit{\kappa }}_{\mathrm{sq}}={\displaystyle \frac{a^{\mathrm{2}}}{\mathrm{12}}}[\mathrm{1}-{\displaystyle \frac{\mathrm{192}}{{\mathit{\pi }}^{\mathrm{5}}}}\sum _{n=\mathrm{0}}^{+\mathrm{\infty }}{\displaystyle \frac{\mathrm{1}}{(\mathrm{2}n+\mathrm{1}{)}^{\mathrm{5}}}}\tanh ((n+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}})\mathit{\pi }\left)\right].\end{array}$$

Numerically, this yields ${\mathit{\kappa }}_{\mathrm{sq}}\simeq \mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{2}}{a}^{\mathrm{2}}$. The permeability of the filter was taken to be equal to ${\mathit{\kappa }}_{\mathrm{filter}}=\mathrm{3.5}\times {\mathrm{10}}^{-\mathrm{2}}{a}^{\mathrm{2}}{\mathit{\varphi }}_{\mathrm{filter}}=\mathrm{8.7}\times {\mathrm{10}}^{-\mathrm{13}}{\mathrm{m}}^{\mathrm{2}}$. The longitudinal dispersivity of the porous matrix was taken to be equal to 0.4 mm, the value obtained by fitting the experimental BTC of column A (homogeneous control column). The dispersivity of the filters was set to 10 µm, which is the characteristic length of the pores of the filters, and the tortuosity was set equal to 1 for all porous domains of the system. It can be noted that the precise values of these last two parameters do not really matter since they do not affect the output of the computer simulations. For the dispersivity of the filter this is due to the thinness of the filter, and for the tortuosity it is related to the smallness of the diffusion term τD₀ in the righthand side of Eq. (5) for the flow rate we investigated.

As for the boundary conditions, a given flow rate was imposed at the inlet of the column and a uniform pressure was imposed at the outlet. For the solute, we considered a concentration flux condition at the entry of the system. To model the injection of a 5 mL volume of tracer solution, we set the concentration flux to 1 during the first 5 mL of injected solution and 0 afterward. Since Eq. (4) is linear in c, the concentration calculated this way is equal to the normalized concentration, whatever the genuine value of the physical concentration of the tracer solution at the inlet of the column.

The flow field within the columns, the temporal evolution of solute concentration maps and numerical BTCs were then computed by solving numerically Eqs. (2), (3) and (4).

3 Results and discussion

3.1 Breakthrough curves

The normalized concentrations measured at the outlet of columns A, B and C, plotted as a function of the number of pore volumes (PV), are depicted in Fig. 3. For the experiments reported in the present section, KNO₃ solutions have been used as conditioning and tracer solutions. Recall that PV is equal to $Qt/V_{\mathrm{0}}$, where V₀ denotes the pore volume of the column and t the elapsed time since the beginning of the injection of the tracer solution. We conducted three identical breakthrough experiments for each column, and the corresponding error bars are shown in Fig. 3.

The BTCs of the homogeneous column (column A) are displayed in Fig. 3a. They have been measured in the presence and the absence of the outlet filter and are both slightly asymmetric bell-shaped curves, a standard shape for columns filled with homogeneous porous media. The two BTCs are nearly indiscernible, which implies that the outlet filter has no impact on solute transport in the homogeneous case.

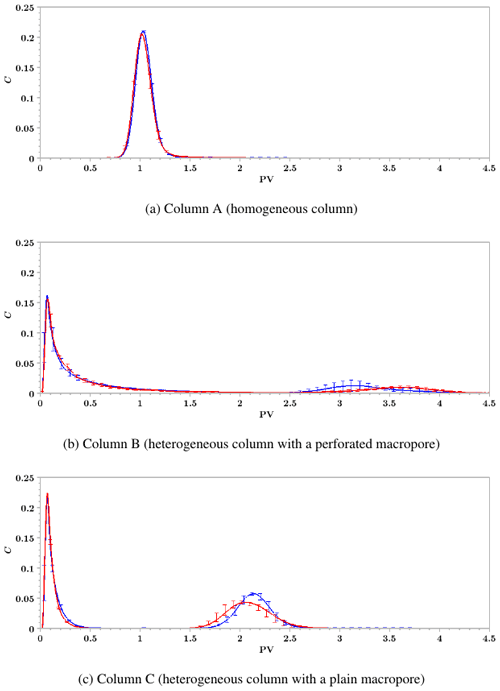
Figure 3 Breakthrough curves showing the normalized concentration, C, as a function of the number of pore volumes, PV, measured at the outlet of columns A, B and C in the presence (blue curve) and the absence (red curve) of an outlet filter. Each breakthrough experiment was conducted three times.

The results are very different for the two macroporous columns B and C. The BTCs measured at the outlet of column B (perforated macropore) are depicted in Fig. 3b in the presence (blue curve) and the absence (red curve) of an outlet filter. The two BTCs share some features, such as the existence of two distinct peaks. The first peak is very asymmetric, with a short ascent followed by a long tail. Breakthrough starts for small values of the number of pore volumes (PV≤0.02) and the maximum of the first peak is reached for PV≃0.05. The second peak is much more symmetric and reaches its maximum after more than three pore volumes. However, the two BTCs differ with respect to the position of the maximum of the second peak. It is located at PV≃3.2 when the outlet filter is present and at PV≃3.6 without any outlet filter. This discrepancy entails that the mean residence time associated with the second peak is affected by the outlet filter. Besides, this mean residence time is directly related to the mean longitudinal pore velocity of the solute giving rise to the second peak of the BTCs. Consequently, the difference in PV means that the flow within the column is affected by the outlet filter.

The analysis of the BTCs of column B gives further insight into the characteristics of the flow field within this column. The decrease of the first peak is surprisingly slow. The normalized concentration remains above zero at least up to PV=1.5, whereas the volume of the macropore is only 1 % of the total pore volume of the system. The slow decrease of the normalized concentration measured at the outlet of column B thus hints at the existence of a substantial solute transfer between the porous matrix and the macropore.

We performed the same kind of experiments by replacing the perforated hollow cylinder used in column B with a plain one to investigate the possible occurrence of such a transfer. The BTCs measured at the outlet of column C are depicted in Fig. 3c in the presence (blue curve) and the absence (red curve) of the outlet filter. The shape of the BTCs is less affected by the outlet filter than for column B. The comparison of Fig. 3b and c shows that the decrease of the first peak is much more pronounced for column C. In this column, by construction, water and solute exchange is prohibited between the macropore and the porous matrix. Thus, the solute entering the column through the macropore (respectively, through the porous matrix) remains in the macropore (respectively, in the porous matrix) throughout its transport within the column. Accordingly, the mass balances corresponding to both peaks are directly related to the fractions of water flowing through the macropore and through the matrix. This is not the case for column B, whose macropore is perforated. Thus, it can experience some solute transfer between the macropore and the surrounding matrix. The difference between the BTCs of columns B and C shows that such solute transfer does occur and explains the long tail associated with the first peak measured at the outlet of column B. Moreover, in contrast with column B, the area below the first peak of column C is less than half of the total area below the BTC, providing further information on the extent of solute transfer between the macropore and the porous matrix in column B.

Finally, for column C, the second peaks reach their maxima for rather similar values of PV (PV≃2.1 in the presence of the outlet filter and PV≃2.0 in its absence). These values are smaller than those observed for column B, which means that the mean longitudinal pore velocity of the solute associated with the second peak is significantly greater in column C than in column B. It shows that besides the alteration of water and solute exchange at the interface between the macropore and the porous matrix, the presence of a plain macropore also modifies the flow field within the column.

3.2 MRI monitoring of Gd³⁺ transport

A set of successive two-dimensional MRI images illustrating the time evolution of Gd³⁺ presence within column B is shown in Fig. 4b and c. These images were taken throughout the injection of the GdCl₃ tracer solution. Due to magnetic field heterogeneity, the images are deformed near the entrance and the exit of the column, leading to the distortion of the column lateral boundary on the images. However, this imperfection does not hinder their qualitative exploitation. Moreover, we also carried out additional breakthrough experiments, this time with GdCl₃ conditioning and tracer solutions (see Fig. 4a). The general features of the GdCl₃ BTCs are similar to those of the KNO₃ BTCs (displayed in Fig. 3b) discussed in the previous section.

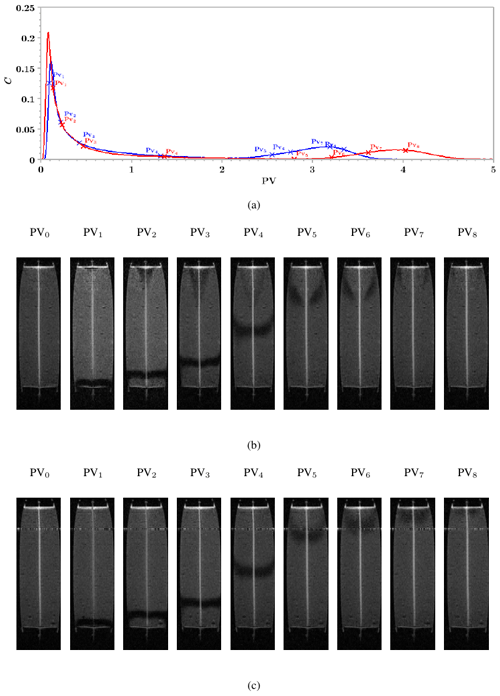
Figure 4 (a) GdCl₃ experimental BTCs measured at the outlet of column B (macroporous column with a permeable macropore) with (blue curve) and without (red curve) an outlet filter. MRI images taken throughout the elution as a function of the number of pore volumes, PV, for column B, with the outlet filter (b) and without the outlet filter (c). Pores volumes corresponding to the time average at which each image has been acquired are reported in (a). The GdCl₃ tracer solution was injected at the bottom of the column and appears dark within the column in the MRI images.

In the successive two-dimensional images displayed in Fig. 4b and c, the grey level of each pixel is sensitive to two parameters, the local porosity (since the column is saturated, the higher the local porosity, the higher the quantity of water in a given small volume and the higher the MRI signal) and the Gd³⁺ local concentration (the higher the concentration of Gd³⁺, the lower the MRI signal) (Haber-Pohlmeier et al., 2017). In the first image of Fig. 4b, before the beginning of the injection, the macropore, where the local porosity is equal to 1, appears in light grey, whereas the surrounding porous matrix, where local porosity ≃0.4, appears in medium grey. In the following images (PV₁–PV₈), some solute is present in the column and its local concentration is positively correlated with the pixel level of darkness.

The transport of Gd³⁺ within the porous matrix can easily be observed, both in the presence (Fig. 4b) and the absence of the outlet filter (Fig. 4c). We start the discussion with the case where the outlet filter is present (Fig. 4b). At PV₁, a dark cone appears just before the outlet filter. Meanwhile, a Gd³⁺ front appears in the porous matrix surrounding the macropore at the bottom of the column. Then, as can be seen at PV₂, the cone extends downwards and laterally towards the lateral boundary of the column. Moreover, the front visible in the porous matrix moves upwards. Subsequently, a brighter zone appears at the centre of the cone (at PV₃), then invading the whole conical region, except along the boundaries of the cone, which remain slightly dark (see PV₄ image). Meanwhile, the Gd³⁺ front continues its ascent into the porous matrix. When the Gd³⁺ front approaches the column outlet and reaches the tip of the cone, it starts to distort (at PV₅ and PV₆) before disappearing (at PV₇ and PV₈). During this last stage, the front is made of two very distorted parts that move away from the macropore and the central part of the column.

In the absence of the outlet filter (Fig. 4c), the situation differs. The MRI images displayed in Fig. 4c show that, in the matrix, the elution front moves upwards with a nearly horizontal shape, except for a small distortion close to the lateral boundary of the columns. This small deformation of the front is probably due to the existence of a slight preferential flow along the lateral boundary of the column (also visible when a filter is present, cf. Fig. 4b). Moreover, the horizontal shape of the front is altered when it approaches the exit of the column (see PV₅–PV₈ images), but to a lesser extent than when the outlet filter is present. We can also notice that the macropore region appears slightly darker at the beginning of the injection (PV₁ and PV₂ images): this change of colour is likely related to the transfer of Gd³⁺ in the macropore. Furthermore, in the absence of the outlet filter, no conical shape appears close to the outlet of the column.

Thus, the strong impact related to the presence of a filter at the outlet of column B, visible on the BTCs and already discussed in the previous section, is also clearly visible in the MRI experiments. When such a filter is present, the time evolution of the solute concentration map within the column is rather complex and displays some marked two-dimensional features. The computer simulations presented in the following section will be helpful to gain a better understanding of the flow processes and their impact on non-reactive solute transport occurring in column B, both in the presence and in the absence of the outlet filter.

3.3 Finite element computations

We solved numerically Eqs. (2), (3) and (4) in a two-dimensional axisymmetric domain representing column B with and without an outlet filter. The modelled BTCs (Fig. 5a) and resident normalized concentration (Figs. 5b and c) are in good agreement with the experimental data presented in Fig. 4. Moreover, the most eye-catching feature related to the influence of the outlet filter on the experimental BTCs, which is its influence on the second peak position, is well reproduced by the numerical BTCs displayed in Fig. 5a. As in the breakthrough experiments (see Fig. 3b), the second peak shifts leftwards, its maximal value increases and its width decreases when the outlet filter is added. On the downside, the modelling of the first peak appears to be challenging and we failed to reproduce quantitatively this portion of the experimental BTCs. Small geometrical details close to the entrance of the column have a sizable effect on the first peak of the numerical BTCs and make it difficult to go beyond the qualitative agreement that we nevertheless highlighted.

The numerical concentration maps are in good qualitative agreement with the MRI images. In the presence of the outlet filter (see Fig. 5b), a conical shape rich in solute appears right after the beginning of the injection close to the exit of the column, as observed in the MRI experiments (cf. Fig. 4b). In addition, the model predicts the progressive fading of this conical shape with the temporary persistence of a solute-rich region along its boundaries (see PV₃ image of Fig. 5b). It also reproduces the upward transport of the solute front within the porous matrix. The front is nearly horizontal during the initial stage of the transport (images PV₁–PV₄ of Fig. 5b) before being strongly distorted while approaching the exit of the column (images PV₅–PV₈ of Fig. 5b), in good qualitative agreement with the images acquired by MRI (cf. Fig. 4b).

The numerically computed concentration maps change significantly when the outlet filter is removed, but the agreement between the calculated maps and the MRI images is still good. In the absence of the outlet filter, the solute remains more concentrated within the macropore at the beginning of the injection, with only a slight diffusion in its surroundings (see images PV₁–PV₃ of Fig. 5c). Moreover, no conical region appears in the vicinity of the exit of the column. Afterward, the model predicts the upward movement of the solute front within the porous matrix, without any distortion and with a progressive exit through the column outlet (images PV₄–PV₈ of Fig. 5c). This pattern is similar to that observed by MRI (Fig. 4c). The sole perceptible difference is that after PV₄, the front is curved upward in Fig. 4c, whereas it remains almost flat in the computer simulations. We believe that this may be due to the existence of a small preferential flow along the lateral boundary of the experimental column.

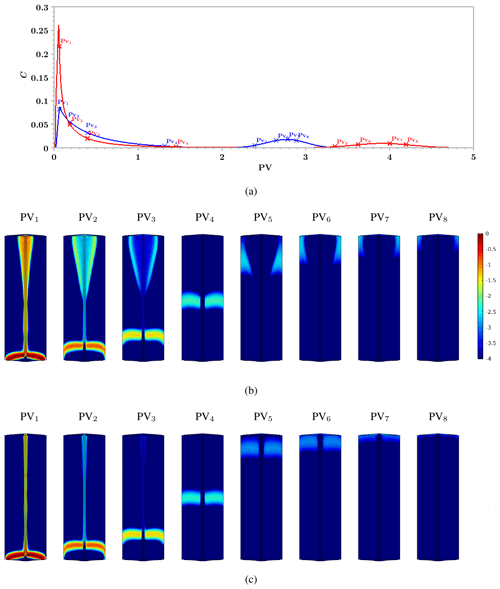
Figure 5 (a) Numerical BTCs calculated for a column with a permeable macropore in the presence (blue curve) and the absence (red curve) of an outlet filter. Solute normalized concentration maps calculated throughout the elution of the solute with the outlet filter (b) and without the outlet filter (c). The scale of the colour bar is logarithmic. The number of pore volumes PV at which the maps have been computed are reported in (a). The solute is transported from the bottom to the top of the domain.

The good overall agreement between the numerical results and the observed data allows us to conclude how the solute is transferred through column B and to explain the effect of the outlet filter. Without the outlet filter, the solute enters the macropore and the matrix. It is then transported through these subdomains with a very moderate solute exchange between them. Only a slight solute spread is visible in the upper part of the macropore (images PV₁–PV₃ of Fig. 5c). Solute concentration maps are similar in the lower half of the column, regardless of the presence of an outlet filter, but drastic changes occur in the upper half of the column depending on the presence of such a filter. The outlet filter triggers a significant solute exchange between the macropore and the matrix, resulting in the appearance of a conical region rich in solute (images PV₁–PV₃ of Fig. 5b). Meanwhile, a fraction of the solute is transported through the matrix, and the corresponding front remains nearly horizontal until it gets sufficiently close to the column outlet. Then, this front experiences a distortion and moves towards the column lateral boundary.

To summarize, the outlet filter routes a fraction of the solute transiting through the macropore to the matrix before the exit of the column. The transport patterns in the presence of a filter also show that the solute transported through the matrix avoids the macropore and the central part of the column when approaching the column outlet.

Figure 6 Various features of the flow field within a macroporous column with a permeable macropore in the presence (first row) and the absence (second row) of an outlet filter. Panels (a) and (d): velocity field streamlines. Panels (b) and (e): logarithmic map of the velocity magnitude of the carrier liquid expressed in m s⁻¹. Panels (c) and (f): radial component of the velocity vector on the matrix–macropore interface (<0 when water flows from the matrix to the macropore and >0 otherwise). The carrier liquid flows from the bottom to the top of the domain.

The effect of the outlet filter on solute transport results from its effect on the flow. We analysed the water flow field to better understand how the presence of the outlet filter modifies the flow and thus impacts solute transport. Various features of the flow field are depicted in Fig. 6. From the analysis of the streamlines (Fig. 6a and d), the velocity magnitude maps (Fig. 6b and e) and the radial component of the velocity field at the interface between the macropore and the matrix (Fig. 6c and f), it is clear that the flow fields, with and without the outlet filter, are similar in the lower half of the column and strongly differ in the upper half. The outlet filter triggers a divergence of streamlines from the macropore to the matrix close to the column outlet (Fig. 6a) and thus a water flux along this direction, as revealed by the positive radial component of the velocity vector at the macropore–matrix interface in the upper half of the column (Fig. 6c). This divergence and the related water flux across the macropore–matrix interface are responsible for the main features visible both in the MRI images (Fig. 4b) and the numerical solute concentration maps (Fig. 5b). Indeed, water routes the solute from the macropore to the surrounding matrix by advection. This flow pattern explains the conical shape associated with solute transport through the macropore (images PV₁–PV₃ of Fig. 5b). The same divergence routes the solute transported through the matrix far away from the centre of the column and thus closer to the column lateral boundary. It explains the strong distortion experienced by the matrix front when it approaches the exit of the column (images PV₄–PV₈ of Fig. 5b). In the absence of the outlet filter, there is no longer any streamline divergence near the exit of the column (Fig. 6d), as the water flux at the macropore–matrix interface vanishes in the upper half of the column (Fig. 6f), yielding the solute to remain in either the matrix or the macropore (images PV₁–PV₈ of Fig. 5c), except for the possible occurrence of transport by molecular diffusion (Batany et al., 2019).

With its very low permeability, the outlet filter acts as a thin layer impeding flow. The effects of embedded layers in macroporous media were already discussed by many authors. For instance, Lassabatere et al. (2004) and Lamy et al. (2013) showed that the amendment of geotextiles in soil columns is an efficient way to homogenize flow and then foster pollutant removal by the matrix. These authors hypothesized that the geotextiles acted as impeding layers and redistributed flow from high permeability conducting zones to lower permeability matrix zones. Even if, in our study, the filter was positioned at the end of the column, the same kind of behaviour seems to occur. The low permeability of the filter acts as a barrier to the preferential flow in the macropore and routes parts of the water and the solute to the matrix.

The analysis of the flow field shows that the same homogenizing effect also occurs at the inlet. Indeed, when filters are present at both extremities, symmetrical streamline distortion and flow field were obtained at the inlet and the outlet of the column. Figure 6a shows the convergence to the macropore of some streamlines having entered the column through the porous matrix after the inlet filter and the divergence to the porous matrix of some streamlines coming from the macropore before the outlet filter, an effect already observed in other MRI studies (Deurer et al., 2004; Greiner et al., 1997). The presence of the inlet filter tends to homogenize the magnitude of the fluid velocity right after the filter. Farther from the inlet filter, when its influence on the flow is no longer felt, the streamlines become almost parallel to the axis of the column. Because of the symmetry of the streamlines in the presence of the outlet filter, this is only visible in the middle of the column in this case (see Fig. 6a), whereas it is apparent in the upper half of the column in the absence of any outlet filter (see Fig. 6d). In the region where streamlines are straight and parallel to each other, the flow is fully developed and the velocity field is similar to the one that one would get in the entire column if the water flow was unidirectional and pressure driven. In the vicinity of the inlet filter, where the flow is not yet fully developed, the carrier liquid velocity increases within the macropore as one goes from the bottom to the middle of the column and simultaneously decreases in the porous matrix because of the incompressibility of the liquid flow (see Fig. 6e and d). However, despite the symmetry of the streamlines between the inlet and the outlet of the column when filters are present at both extremities, solute transport seems to be visually rather unaffected by the presence of an inlet filter. Images acquired by MRI (Figs. 4b and c) and computer simulations (Figs. 5b and c) show that the solute front is nearly horizontal in the lower half of a macroporous column containing a perforated macropore. The presence of the inlet filter probably alters the mass partition between the macropore and the surrounding matrix, but it does not give rise to a distortion of the solute front like the one generated by the diverging flow pattern induced by the presence of the outlet filter. However, these observations do not rule out the possible existence of inlet effects, which could be not straightforward to discern in the MRI images or the calculated concentration maps.

3.4 Limitations

The magnitude of the exit effect highlighted in Sect. 3.1, 3.2 and 3.3 is necessarily dependent on the geometry of the column (e.g. the ratio of the diameter of the macropore to the diameter of the column and the ratio of the macropore to the column lengths) and on the permeability of the surrounding porous medium. For instance, the importance of the flow in the porous matrix is related to the matrix permeability and to the surface area ratios between the macropore and the matrix (Batany et al., 2019; Lamy et al., 2009). If a macropore with a smaller diameter had been used, the two peaks visible on the BTCs would have been closer to each other and would have eventually merged had the diameter of the macropore been small enough. Indeed, in the limit where the diameter of the macropore tends to zero, the system becomes homogeneous and its BTC then displays a single peak. In this limit case, previous MRI studies do not show any discernible exit effect at the level of the images (Lehoux et al., 2016); nevertheless, some conflicting results about the dispersion coefficient suggest that boundary effects are still present within homogeneous columns.

If a macropore with a wider diameter or a less permeable matrix had been used, the magnitude of the exit effect may have been larger than the one we observed. However, because of the symmetry of the streamlines when filters are present both at the inlet and the outlet of the column (see Fig. 6a), the possible level of enhancement of the exit effect in this case is not clear. Moreover, measuring BTCs at the outlet of a heterogeneous system with a greater velocity contrast between the macropore and the matrix than in our study could quickly be very time consuming, since the smaller the pore velocity in the matrix, the longer it takes for the solute transported within the matrix to exit the column (and the lesser the fraction of the solute transported within this domain). The geometry of the heterogeneous columns studied in this work was precisely tuned to avoid this potential experimental pitfall.

4 Conclusions

In this study, we investigated the effect of an outlet filter on solute elution and on the time evolution of concentration maps in homogeneous and macroporous columns, considering both perforated (i.e. permeable) and plain (i.e. impermeable) macropores. For this purpose, we combined (i) column breakthrough experiments with tracer solutions (KNO₃ and GdCl₃), (ii) MRI experiments to monitor Gd³⁺ transport within columns and (iii) computer simulations of water flow and non-reactive solute transport.

While the breakthrough curve is unaffected by the presence of an outlet filter when the column is homogeneous, this is no longer true for macroporous columns, especially when the macropore is permeable to water and solute fluxes. The numerical results show that the presence of filters (at the outlet, but also at the inlet) can impact the flow of the carrier liquid over a significant part of the column. The flow can display some substantial non-unidirectional features associated with entrance–exit effects. Such finite length effects are expected to be less pronounced as the ratio between the length of the column and its diameter increases, but increasing this ratio is not always an option (e.g. because it entails the use of a greater amount of material and of stock solutions, or because the columns may have to be small due to experimental constraints).

A simple one-dimensional transport model will not necessarily be appropriate, even when $L/d_{\mathrm{col}}=\mathrm{3}$ (the ratio we have worked with in this study). Indeed, when it comes to fitting the experimental data accurately, good knowledge is required regarding (i) the stationary flow within the system and (ii) the effect of the various elements of the experimental apparatus on solute transfer between domains differing in their hydraulic properties. For different experiments to be reliably exploited and compared, there is a need to report the geometric features of the column and the boundary devices employed when performing transport experiments with heterogeneous media (frits or filters, reservoirs, incoming tubes, etc.). It might only be possible to relate transport parameters to porous medium properties by taking into account the whole experimental apparatus employed. This issue is generic, but it should be kept in mind that the magnitude of the exit effect probably depends on the specifics of the system used. The transport properties of experimental systems, such as the one reported in this study, can be strongly impacted by this effect. In such cases, careful consideration of the potential impact of the geometry of the column and the additional boundary devices is required to be able to draw some quantitative estimates from a one-dimensional transport model based on experimental data obtained with macroporous columns, where water flow can display some non-unidirectional features. In any case, more in-depth studies devoted to this subject are certainly needed.