the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Water sharing policies conditioned on hydrologic variability to inform reservoir operations
Guang Yang
Paul Block
Water resources infrastructure is critical for energy and food security; however, the development of large-scale infrastructure, such as hydropower dams, may significantly alter downstream flows, potentially leading to water resources management conflicts and disputes. Mutually agreed upon water sharing policies for the operation of existing or new reservoirs is one of the most effective strategies for mitigating conflict, yet this is a complex task involving the estimation of available water, identification of users and demands, procedures for water sharing, etc. A water sharing policy framework that incorporates reservoir operating rules optimization based on conflicting uses and natural hydrologic variability, specifically tailored to drought conditions, is proposed. First, the trade-off between downstream and upstream water availability utilizing multi-objective optimization of reservoir operating rules is established. Next, reservoir operation with the candidate (optimal) rules is simulated, followed by their performance evaluations, and the rule selections for balancing water uses. Subsequently, a relationship between the reservoir operations simulated from the selected rules and drought-specific conditions is built to derive water sharing policies. Finally, the reservoir operating rules are re-optimized to evaluate the effectiveness of the drought-specific water sharing policies. With a case study of the Grand Ethiopian Renaissance Dam (GERD) on the Blue Nile river, it is demonstrated that the derived water sharing policy can balance GERD power generation and downstream releases, especially in dry conditions, effectively sharing the hydrologic risk in inflow variability among riparian countries. The proposed framework offers a robust approach to inform water sharing policies for sustainable management of water resources.
- Article
(10809 KB) - Full-text XML
- BibTeX
- EndNote
Rapid population growth and socioeconomic development exacerbate stress on the management of water resources globally (Vörösmarty et al., 2000; WWAP, 2019). The effective management of surface water reservoirs is one of the most efficient means for reducing this stress by reallocating water resources spatially and temporally (Gaudard et al., 2014). Thus, in recent decades, many models and strategies have been investigated to inform and improve reservoir operation decision-making (Chaves and Chang, 2008; Cancelliere et al., 2002; Herman and Giuliani, 2018; Karamouz and Houck, 1982; Giuliani et al., 2014; Oliveira and Loucks, 1997). For example, Karamouz and Houck (1982) optimize monthly reservoir releases by deterministic dynamic programming and build a linear reservoir operation model conditioned on the relationship between optimal releases and reservoir state variables. Cancelliere et al. (2002) built a nonlinear reservoir operation model by using neural network techniques to improve reservoir irrigation water supply during drought conditions. Herman and Giuliani (2018) design a tree-based policy which is flexible and interpretable for reservoir operation over multiple timescales. In general, reservoir decisions (e.g., water releases and power generation) are determined using reservoir operating rules with available input variables, including reservoir state (e.g., reservoir water level) and hydrological conditions (e.g., reservoir inflow; Oliveira and Loucks, 1997).
Reservoir operating rules are typically derived using fitting-based and simulation–optimization-based approaches. In fitting-based rules derivation (policy fitting), reservoir operation decisions are optimized and subsequently fitted with input variables using linear regression (Bhaskar and Whitlatch, 1980), artificial neural networks (Cancelliere et al., 2002), fuzzy inference (Chang and Chang, 2001), and decision trees (Wei and Hsu, 2008). In simulation–optimization methods, the parameters of reservoir operating rules are optimized with an iterative simulation-based search algorithm in which the performance is evaluated directly from reservoir operation simulations (Le Ngo et al., 2007; Rani and Moreira, 2010). For example, Giuliani et al. (2015a) approximated reservoir operating rules by using artificial neural networks and radial basis functions (RBFs) and optimized the rules for multi-purpose water reservoirs with an evolutionary algorithm. A policy fitting approach requires an optimal set of reservoir inflows, storages, and releases, and its effectiveness highly depends on the performance of the optimized reservoir operation model; however, the rules derivation is interpretable and intuitive when optimal reservoir decision-making is highly correlated with state variables. In contrast, simulation–optimization-based approaches do not rely on existing optimal reservoir operations, and thus, it is generally more flexible than fitting-based rules.
Most of these approaches are implemented in water resources systems contained within a basin or jurisdiction in which the benefits (e.g., power generation, water supply, and ecosystem function maintenance) can be quantified and evaluated (Reddy and Nagesh Kumar, 2007; Feng et al., 2018; Yang et al., 2016). Reservoir operations are necessarily more complex after considering a wide variety of social, political, economic, and cultural conditions in river basins (Zeitoun and Mirumachi, 2008). Disputes and conflicts are not uncommon between riparian states in river basins when water sharing agreements are nonexistent or nonenforceable, and claims may be defined based on historical use. For example, the Nile river serves 11 countries, 250 million people (Nile Basin Initiative, 2017), and is vital to agriculture, industry, and hydropower (Paisley and Henshaw, 2013), yet no mutually agreed upon water sharing policies exist. The 1959 agreement (Guariso and Whittington, 1987) has been repudiated by upstream riparian states. Acknowledging significantly divergent interests and a history of conflict and distrust, quantifying the impact of reservoir operation on downstream benefits is challenging, hindering the development of water sharing strategies (Link et al., 2016).
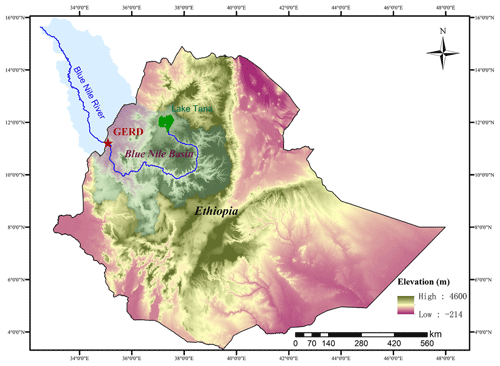
Figure 1Blue Nile basin with Ethiopia's country borders and the location of the Grand Ethiopian Renaissance Dam (GERD) reservoir.
According to the Transboundary Freshwater Dispute Database (McCracken and Wolf, 2019), the existing 310 international river basins across the world are shared by 150 countries and disputed areas, cover 45 % of the Earth's land surface, and contribute to 60 % of the world's freshwater resources. As suggested by Sadoff and Grey (2002), it is critical to understand and account for the range of interrelated benefits resulting from the development of international rivers in a cooperative way. Such cooperation of water resources development in international river basins has been widely investigated in recent years (Li et al., 2019; Luchner et al., 2019; Arjoon et al., 2016; Wheeler et al., 2018; Degefu et al., 2016). For example, Arjoon et al. (2016) proposed a benefit sharing method based on the optimization results from a hydro-economic model and evaluated the value of cooperative water management in the eastern Nile river basin. Li et al. (2019) analyzed the water benefits of stakeholders from cooperation under different reservoir operation scenarios by using cooperative game theory methods. Luchner et al. (2019) simulated reservoir operations and water allocation in an international river basin in Central Asia and found that international cooperation in the power sector can ease the conflict between upstream hydropower production and downstream irrigated agriculture.
Most previous studies focus on illustrating the importance of a cooperative strategy through water system optimization and simulation (Dombrowsky, 2009; Tilmant and Kinzelbach, 2012) and evaluating the benefits of cooperative operation (Goor et al., 2010; Anghileri et al., 2013; Uitto and Duda, 2002; Luchner et al., 2019). There is less literature (Wheeler et al., 2016; Li et al., 2019; Degefu et al., 2016; Teasley and McKinney, 2011), however, addressing strategies for reaching an agreement or consensus on water resources development amongst downstream and upstream riparian countries. Also, although cooperation can result in a win-win situation for both downstream and upstream stakeholders, cooperative water use strategies are obstructed by single-sector interests, especially when long-term commitments are involved (Wu and Whittington, 2006). More specifically, it is often difficult to achieve a mutually agreed upon cooperation strategy, given divergent solution preferences by stakeholders.
Additionally, benefit sharing policies rely heavily on hydro-economic modeling and cost–benefit analysis (Jeuland et al., 2014), which strives to maximize overall aggregated benefits and subsequently allocate benefits in an equitable way. However, (1) the aggregation of benefits can hide important trade-offs and may increase the risk of floods and droughts for maximum economic benefit. (2) There is no standard that regulates how benefits of water use from various sectors (e.g., drinking, agriculture, industry, recreation, and navigation) are quantified and what mechanism should be applied to equitably allocate or share the benefits (Acharya et al., 2020). And, (3) there is presently no basin-wide authority that enforces benefit allocations (e.g., payments from one country to another), although institutions such as the Nile Basin Initiative could serve in this role (Arjoon et al., 2016). Thus, water sharing policies that consider the trade-off between economic benefits and drought risk, rather than benefit sharing policies based on cooperative operation strategies analysis, are investigated in this study. The policies will be flexible, interpretable, and, more importantly, drought-focused, such that downstream drought mitigation will become an inherent part of the water sharing framework.
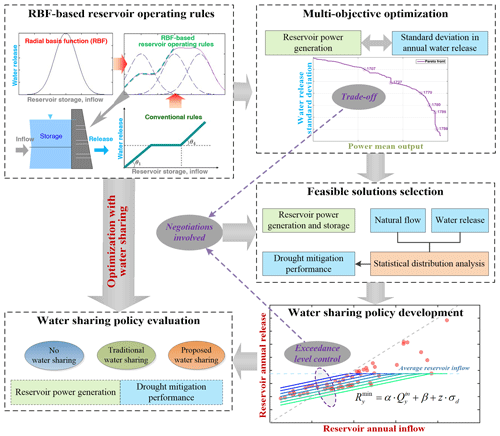
In this study, a systemic framework is proposed to derive operational reservoir water sharing policies using multi-objective optimization for water use conflict mitigation. Specifically, this includes (1) optimizing reservoir operating rules and establishing trade-offs between upstream benefits and downstream drought risks; (2) simulating reservoir operation with the candidate (optimal) rules, evaluating performance, and selecting the most suitable rules for balancing benefits; (3) deriving water sharing policies conditioned on reservoir operations and water availability; and (4) re-optimizing reservoir operating rules incorporating derived water sharing policies to evaluate effectiveness and performance. The drought-focused water sharing policies are interpretable as they are derived from and evaluated on reservoir operation simulations from existing optimal rules. Furthermore, the policies are considered flexible by offering opportunities for informing upstream–downstream negotiations. The Grand Ethiopian Renaissance Dam (GERD) in Ethiopia is selected to demonstrate the framework and illustrate how operational water sharing strategies, reflective of upstream and downstream demands and natural hydrologic variability, can promote water sharing agreements between upstream and downstream countries.
The Blue Nile river, the largest tributary of the Nile river, originates at Lake Tana in Ethiopia and merges with the White Nile river in Khartoum, Sudan. Average annual rainfall in the upper part of the basin varies between 1200 and 1800 mm per year (Conway, 2000), with a dominant rainy season in June–September contributing approximately 70 % of mean annual precipitation. During this season, the Blue Nile contributes nearly 80 % of the total Nile river streamflow (Swain, 2011), and the average annual runoff of the Blue Nile at Roseries, near the Ethiopia–Sudan border, is approximately 49 km3 per year (Wheeler et al., 2016); thus it plays a significant role in livelihood and development in Ethiopia, Sudan, and Egypt.
Ethiopia started constructing the GERD across the Blue Nile river in 2011, approximately 15 km upstream of the Sudanese border (Fig. 1). When completed, the GERD will become the largest hydroelectric dam (installed capacity more than 5000 MW) in Africa (Government of Ethiopia, 2020) and will have a total reservoir capacity of 74 billion m3. The GERD is expected to produce an average of 15 130 GWh of electricity annually (with a mean output of 1727 MW; Tan et al., 2017; Tesfa, 2013), which will contribute to Ethiopia's national energy grid and feed the East African power pool (Nile Basin Initiative, 2012). There is uncertainty in media reports regarding the total installed capacity for GERD, which ranges from 5150 MW (Ezega News, 2019b) to 6000 MW (Ezega News, 2019a; Zelalem, 2020). A value of 6000 MW, which was applied both in the annual electricity production estimation and previous publicly available scientific studies (Tesfa, 2013; Yang et al., 2021), is chosen for this study. It is worth noting that rerunning the simulations with an installed capacity of 5150 MW instead of 6000 MW does not change principal conclusions. Although the GERD is primarily designed for hydropower, and is thus non-consumptive, operating to maximize power generation may result in a water release schedule significantly different from the natural annual cycle, particularly considering drought periods, with implications to Sudan and Egypt. This is the crux of the current hydro-political confronting the riparian countries.
In this study, GERD reservoir operation rules are developed, considering the power generation and downstream water release (including turbine outflows and spillage losses) simultaneously to mitigate upstream–downstream water use conflicts, and are particularly tailored to drought periods. The study investigates water sharing (drought mitigation) policy derivation procedures (reservoir operation simulation and optimization, power generation and downstream water release analysis, and drought mitigation policy extraction and validation), balancing GERD production and downstream flow volumes. Historical monthly inflow at the El Diem gauging station (located just downstream of the GERD site) for 1965–2017 (Fig. 2) is applied.
The procedure for water sharing policy derivation and evaluation including large-scale reservoir operations is introduced in this section (Fig. 3). In summary, the process is as follows:
-
First, optimize the reservoir operating rules approximated with radial basis functions (RBFs) and obtain the Pareto front for upstream and downstream benefits trade-off.
-
Second, select feasible solutions on the Pareto front according to the requirements of power generation and drought mitigation; specifically, for a given power generation level, the distribution of annual water release is analyzed with special attention to low-flow years.
-
Third, define the relationship between annual reservoir inflow and releases based on the selected feasible solutions; the policy can be further framed as a function of reservoir annual inflow predictions.
-
Fourth, incorporate the policy into general RBF-based rules to evaluate policy effectiveness and robustness.
3.1 Reservoir operation model
The primary purpose of the GERD reservoir is hydropower production; this objective function can be described as follows:
where E is hydroelectricity generation (kilowatt-hours) during the total number of operational periods T, Pt is the power generation output (kilowatts) during the time period t, and Δt is the time (hours) of a single period. η, g, and ρ refer to the dimensionless hydropower generation efficiency of the turbines (set as 0.9 in this study), gravitational acceleration (9.8 m/s2), and water density (1000 kg/m3), respectively. and are reservoir release for power generation (cubic meters per second) and average power head (meters) in period t, respectively.
In lieu of modeling specific water requirements downstream of the GERD, minimizing annual water release variance is applied. This approach favors reliable releases, yet also reflects natural hydrologic variability, and can be described as follows.
where is the reservoir water release (which includes turbine outflows and spillage losses) in year y and and are the mean value and standard deviation of reservoir annual water release across all Y operational years, respectively.
Physical and operational reservoir constraints are listed follows.
- (a)
Water balance.
where St and St+1 are reservoir storage (m3) in period t and t+1, respectively. represents reservoir inflow (cubic meters per second) in period t, is reservoir release (cubic meters per second) in period t, and EPt is the sum of evaporation and seepage from the reservoir (cubic meters per second) in period t.
- (b)
Reservoir capacity limits (Jameel, 2014).
The reservoir structural and operational constraints can be expressed as follows:
where Smin and Smax are the minimum (14.8 billion m3) and maximum (74 billion m3) allowable reservoir storage. Additionally, Sbegin and Send represent the initial and final reservoir storage (cubic meters per second) for simulations (both of them are set as 65.1 billion m3), respectively, and are prescribed as follows:
- (c)
Reservoir release limits.
The reservoir release constraints are expressed as follows:
where QLt and QUt are the minimum and maximum release (cubic meters per second) in period t, respectively. The expected guidelines for GERD reservoir water release are not explicitly available; thus, releases are set higher than zero and lower than the maximum reservoir inflow (21.9 billion m3 per month) during the high-flow season to reduce or eliminate downstream floods.
- (d)
Power generation limits (Tesfa, 2013).
where PLt and PUtare the minimum (0 MW) and maximum (6000 MW) power limits in period t, respectively.
3.2 Reservoir operating rules
In this study, reservoir water releases are conditioned on radial basis functions (RBFs), a nonlinear function approximating method (Buşoniu et al., 2011) which can provide universal approximation (Tikk et al., 2003) and ensure a flexible reservoir operating rules structure. For more applications of RBF models in reservoir operation, see Giuliani et al. (2015a). The reservoir operating rules are defined as follows.
where U is the number of RBFs, φ(⋅) and ωu are the weights of the uth RBF, M is the number of input variables Xt, and cu and bu are the M-dimensional center and radius vectors of the uth RBF, respectively.
Because water release generally depends on the reservoir state (Revelle et al., 1969) and inflow, with intra- and interannual variability, reservoir storage St, inflow , and seasonal information τt (where τt refers to the position of the current period (month) t within a water year) are selected as input variables, and .
In this study, the number of RBFs is set to four (as in Giuliani et al., 2015b); thus U=4 and M=3 (three input variables) in Eqs. (8) and (9), resulting in 20 parameters in the RBF-based rules. The parameters in RBF-based rules are optimized with a simulation–optimization model (Rani and Moreira, 2010), using the Pareto archived dynamically dimensioned search (PA-DDS) evolutionary algorithm which has been successfully applied to reservoir operating rules optimization (Yang et al., 2020). The procedure of the PA-DDS algorithm has been described in detail by Asadzadeh and Tolson (2013).
3.3 Drought-focused water sharing policy
To ensure downstream water supply, the GERD reservoir will need to be operated under minimum annual water release constraints. Apart from the RBF-based rules determining the reservoir water release in each time step (months), a drought mitigation policy is also adopted to address dry periods. The policy is based on annual time steps and is represented as a linear regression between annual reservoir inflow and water release. More specifically, the minimum annual reservoir water release can be determined by the following equation:
where and refer to reservoir inflow and minimum reservoir water release during year y, respectively. α and β are regression parameters estimated from simulations containing reservoir inflow values below the historical average (approximately 49 billion cubic meters per year – BCM per year). An exceedance parameter z is multiplied by the standard deviation of the regression residuals σd to vary how conservative the drought mitigation policy is (see Fig. 4 for a visualization of exceedance parameters). This policy design favors downstream releases under drought conditions by supplementing what would occur under natural flow conditions; however, as a trade-off, the minimum reservoir release in any year will not exceed the historical average reservoir inflow (see the horizontal line in Fig. 4).
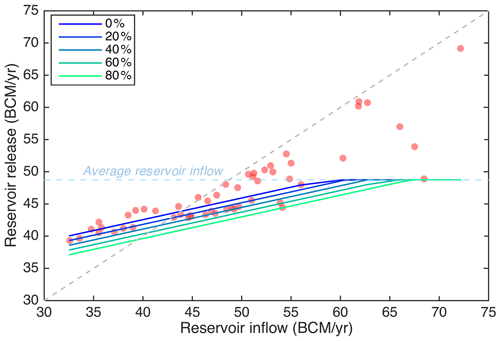
Figure 4Sample drought mitigation policy with varying exceedance levels (z=0 %, 20 %, 40 %, 60 %, and 80 %).
The drought policy is conditioned on reservoir inflows and releases for a transparent, interpretable, and intuitive process, which is important especially when negotiations are involved. The gradient of the policy line is highly correlated with variability in reservoir releases; in general, as the slope increases, so does the variability in releases. Thus, the parameter α can be estimated from the trade-off between reservoir power generation and downstream water release variability. The exceedance parameter z further controls the degree of drought mitigation; larger z values indicate higher drought thresholds (see the intersection between the policy line and 1:1 dash line in Fig. 4). In the drought policy design, these two parameters can be estimated separately to isolate their impact on drought mitigation performance. This case study mainly focuses on the impact of the first parameter as the exceedance parameter z is eventually set as 0 %.
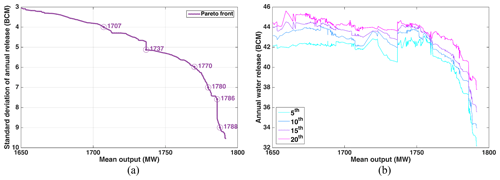
Figure 5Multi-objective optimization results of reservoir operating rules in terms of (a) Pareto front and (b) the relationship between power generation and the 5th, 10th, 15th, and 20th percentile of annual water release.
In this study, the drought mitigation policy is designed with annual streamflow data; however, reservoir operating rules are derived for monthly operation. With reservoir storage in the current month Sm, reservoir inflow in the current month , and the predicted reservoir inflow during the rest of the year , … , , the reservoir water release in the current month and the rest of year , … , can be obtained from Eqs. (8) and (9). Thus, the annual reservoir inflow and water release can be estimated as follows.
The minimum reservoir water release in year y can be estimated from Eq. (10) as . To ensure the minimum annual water release obligation is met, if the estimated annual reservoir water release is lower than , the release in current month will be corrected according to the following:
The estimated variables , , and are updated in each time step. In the last month of each year, the annual reservoir inflow estimation will be equal to actual annual inflow , and the estimated minimum annual release will be . If , the reservoir water release in the last month will be corrected as , and the will be equal to . Thus annual reservoir release will always be greater than or equal to the specified minimum reservoir water release , and it can be inferred that the minimum annual release is mainly determined by the policy parameters α, β, and z rather than forecast accuracy.
As illustrated in Eq. (10) and Fig. 4, the minimum annual reservoir release can be estimated from the annual reservoir inflow after the drought policy line is determined. Considering actual annual reservoir inflow will not be available until the last month of each year, the annual reservoir inflow forecast is used instead. In this study, both a climatology inflow forecast ( set as the long-term average streamflow for that month) and a perfect inflow forecast ( set to observed reservoir inflow ) are used to evaluate the performance of the drought mitigation policy. To avoid adverse downstream and upstream flood caused by spillage, both the monthly and annual water release will be less than the maximum reservoir inflow in flood seasons and wet years.
4.1 Multi-objective reservoir operation with no drought policy
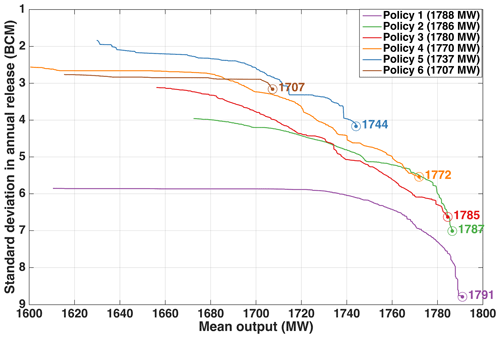
Multi-objective optimization of GERD reservoir operating rules illustrates that there is a trade-off between reservoir power generation and deviation in reservoir annual water releases (Fig. 5a). More specifically, GERD monthly mean power generation output is estimated at 1788, 1708, 1737, and 1707 MW for annual release standard deviations of 9, 7, 6, 5, and 4 BCM per year, respectively. Although the reservoir operating rules are not optimized for maximum annual water release, less typically leads to relatively more releases in dry conditions (e.g., 5th, 10th, 15th, and 20th percentiles), especially when the mean output is greater than 1750 MW (Fig. 5b). Thus, downstream countries may benefit more from reservoir operating rules favoring smaller in drought conditions; this trade-off between power generation and can be used to balance GERD power generation and downstream water use benefits. There also exists a trade-off between and other power indicators, such as firm output (see Fig. A1 in Appendix A).
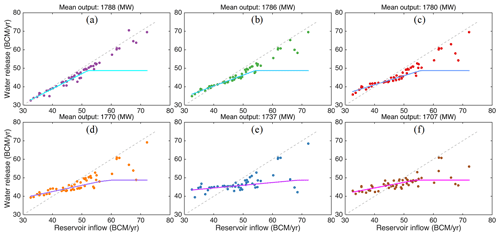
Figure 7Relationship between annual reservoir inflow and water release (points) and the corresponding drought mitigation policy (lines) for various power generation levels.
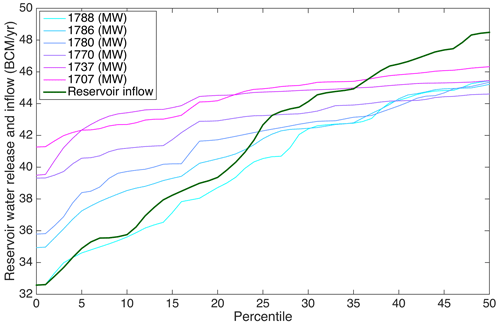
Figure 8Percentiles of annual reservoir inflow and water release under various power generation levels.
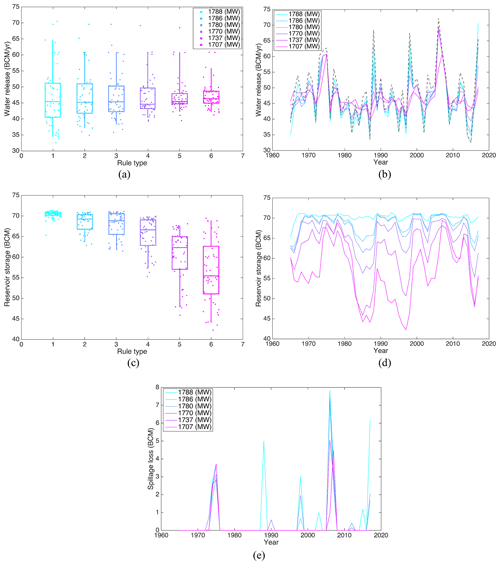
The reservoir operating rules simulation results under various mean output levels illustrates that the variance in annual water release shrinks, and reservoir storage declines as power output decreases (Fig. 6). Although the median values of annual water release for all six output levels are approximately the same (around 45 BCM per year), the reservoir operating rules with more output generally have lower minimum water releases (Fig. 6a, b), especially in dry periods. In general, greater reservoir storage leads to more power generation (see Eq. 1) and vice versa; thus, the reservoir operating rules generating 1788 MW of mean output produces the highest water level and 1707 MW the lowest (Fig. 6d). Also, there is a clear trade-off between the variance in reservoir storage and water release (Fig. 6a, c); smaller reservoir storage variance ensures higher reservoir levels, greater water release variance, and lower minimum water releases. It is worth noting that the 75th and 90th percentiles of reservoir storage are much more sensitive to power output than those of water release. More specifically, the 90th percentile of water release for rule types 5 and 6 are almost the same; however, the corresponding percentile of reservoir storage (and power output) are notably different (Fig. 6a, c). This indicates that rule type 6 may be inferior to rule type 5 despite the trade-off in Fig. 5a. Thus, it is necessary to analyze the operation results (including water release and power generation) before selecting the reservoir operating rules based on the Pareto front in Fig. 5a.
Comparing across rule types, rules with a high mean output of power generation generates more hydropower mainly in wet years. In particular, rule type 1 (1788 MW) can generate approximately 670, 760, and 670 MW more than rule 6 (1707 MW) in years 1988, 1998, and 2017, respectively. In these years, the annual reservoir inflow is greater than 65 BCM per year (Fig. 6b). It is worth noting that the annual reservoir inflow in the previous 1 or 2 years (i.e., year 1987, 1997, and 2015) is less than 38 BCM per year (Fig. 6b), and the reservoir storage of rule type 1 is much higher than in other rule types (Fig. 6d). Thus, it can be inferred that rule types with larger power generation can increase the mean output by releasing less water during dry years to maintain relatively higher reservoir water levels. In this way, more water will be available, and higher head ( in Eq. 1) can be achieved for future wet years, leading to much more power generation.
However, releasing less water in dry years is not a strategy preferred by downstream countries. Although downstream releases are always greater than the minimum natural GERD inflow (which occurs in 2015), releases may clearly be less than natural flow in some dry years (e.g., 1965 and 1997; see Fig. 6b), which may aggravate drought conditions. According to the relationship between annual reservoir inflow and water release simulated from rule type 1, water release is less than reservoir inflow in most cases (Fig. 7a). In comparison, rule type 3 (1780 MW) releases more water than reservoir inflow in dry years. As power generation decreases further, the number of years with reservoir water releases exceeding inflow increases. By applying a linear regression between annual reservoir inflow and water release (see the lines in Fig. 7), a drought mitigation policy (Eq. 10) can be extracted to constrain annual water release in reservoir operation. Rule types favoring more power generation generally produce a steeper gradient in the drought mitigation policy.
4.2 Drought policy selection and analysis
To select the most suitable drought mitigation policy, both the corresponding power generation and reservoir release benefits in drought years may be evaluated. In this study, the annual reservoir release amount and the deviation in annual releases are used as proxies for downstream benefits. For example, if annual releases during drought years are greater than annual reservoir inflow (or natural flow), downstream droughts are partially mitigated. In general, the statistical distributions of annual reservoir inflow and releases are significantly different when reservoir operations are tailored to drought mitigation. This difference is more pronounced for lower power generation levels (see Fig. A2 in Appendix A). Considering low flows, the 10th percentile of water releases increases as hydropower generation decreases, from 35.6 BCM per year for rule type 1 (1788 MW) to 42.7 BCM per year for rule type 6 (1707 MW). Except for rule type 1, all rule types ensure that the 10th percentile of releases is greater than the 10th percentile of annual reservoir inflow (35.8 BCM per year). This equates to supplementing downstream flows to address drought conditions when the 10 % exceedance value of annual reservoir inflow is used as the drought threshold. Furthermore, even when reservoir inflow is less than its 20th percentile value, water releases are greater than annual reservoir inflow, except for rule type 1 (Fig. 8). However, when the threshold exceeds the 25th percentile, only solutions based on rule types 3–6 contain annual releases surpassing inflow. These distributions (Fig. 8) can provide critical insights during riparian negotiations regarding trade-offs between power generation and supplementing downstream flows during drought conditions. Although only six candidate solutions are illustrated here, more representative solutions may be analyzed in practice.
By incorporating these drought policies (Fig. 7), reservoir operating rules are optimized again for maximum power generation and minimum deviation in annual release volumes, illustrating varying trade-offs for drought policies 1–6 (Fig. 9). Drought policies produce similar but not exact hydropower generation as the original operating rules (e.g., policy 1 original is equal to 1788 MW; drought is equal to 1791 MW). The standard deviation in annual releases also does not change significantly. Comparing drought policies producing a high level of hydropower production (e.g., moving from policy 1 to 2), a small trade-off in production (∼4 MW) leads to approximately a 2 BCM per year decrease in the standard deviation in annual releases. For lesser hydropower production policies (e.g., moving from policy 5 to 6), a larger difference of 37 MW leads to a smaller (∼1 BCM per year) change in the standard deviation in annual releases. Also, rules including a drought mitigation policy tend to have a greater mean output, and 10th percentile water releases, but lesser standard deviation in annual water release, spillage loss, and evaporation loss than original rules (see Fig. A3 in Appendix A).
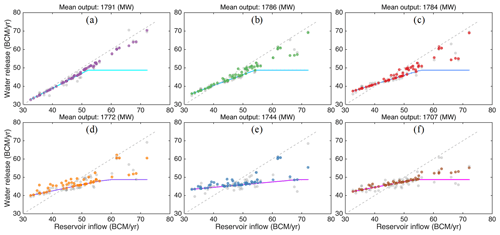
Figure 10Relationship between annual reservoir inflow and releases using re-optimized reservoir operating rules. The drought policies are represented by lines, and the gray points refer to the inflow and release relationship from which drought policies are derived.
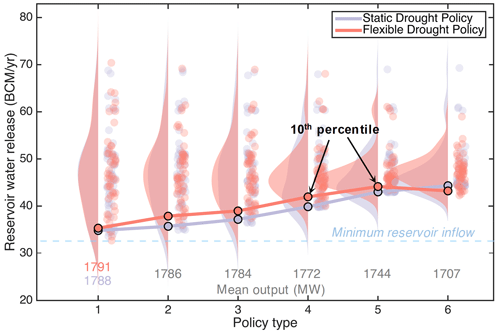
Figure 11Comparison of reservoir operations using flexible and static drought policies based on power generation output and water release distribution analysis. Policy type 1 refers to the comparison with a similar statistical distribution of water releases. Policy types 2–6 refer to comparisons with similar power generation outputs.
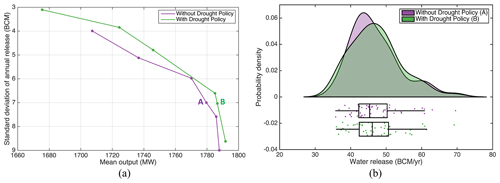
After re-optimization with the drought policy information included, greater power generation and smaller values of the standard deviation in annual water releases are produced. More importantly, the re-optimized rules can fully ensure minimum annual releases under different reservoir inflow levels (Fig. 10). The reservoir operation results of the proposed drought policy are compared with those of conventional drought or water sharing policies. A conventional water sharing policy here refers to a guaranteed quantity or minimum flow strategy, i.e., GERD will guarantee a fixed volume of water release each year. Compacts adopting this strategy in whole or in part include the Colorado River Compact, Arkansas River basin Compact, and Sabine River Compact (68 Stat., Chapter 690, 1953; McCormick, 1994; Draper, 2006). A comparison (Fig. 11) indicates that the flexible drought policy proposed here can generate more power than a conventional (static) drought policy with a similar statistical distribution of water releases. In addition, flexible policies can better mitigate drought conditions (see the kernel distribution as well as 10th percentile of water releases in Fig. 11) than static policies for similar power output levels. This is because the flexible policy is derived from optimal reservoir operation results, which tends to generate more power. In contrast, the static policy (which is presented as a horizontal line instead of sloped lines in Fig. 10) transfers the risk of water shortages (or hydrologic variability) completely to the upstream GERD, which will limit GERD's ability to produce more power.
These re-optimized rules produce slightly more power than the original rules for the equivalent standard deviation of annual release values (Fig. 12a) even though they are re-optimized and constrained on annual water releases for drought conditions. Performance of the re-optimized rules, however, mainly depends on the exceedance parameter z in Eq. (10); more conservative drought mitigation policies (with larger z values) can generate more power. Because the trade-off between power generation and the standard deviation in annual releases is similar between the original rules and drought policy rules (Fig. 12b), it is feasible to base negotiations on the original rules in this case, as the expected drought policy outcomes are superior.
Reservoir operations in river basins will become more complex after considering diverse and potentially conflicting objectives between upstream and downstream stakeholders. With the water sharing policy framework proposed here for the Grand Ethiopian Renaissance Dam on the Blue Nile river, a relationship between downstream and upstream water availability is established, water sharing policies are derived from multi-objective optimization results of reservoir operating rules, and the effectiveness of these policies during drought periods is analyzed. It is demonstrated that a framework incorporating RBF-based rules and a drought-focused water sharing policy can lead to robust reservoir decision-making. There is a clear trade-off between power generation and the standard deviation in reservoir releases; however, effective policies are available to balance this trade-off, even when considering drought periods.
It is worth noting that there are limited drought periods in the historical streamflow time series, which may lead to greater uncertainty in water sharing during severe droughts and may result in the underestimation of the impact of hydrologic variability on GERD operations. To address this, the GERD inflow record could be extended by relating it to other long-term gauging stations in the Nile basin to capture more historical droughts and better characterize hydrologic conditions for enhanced policy design. In addition, the trade-off in objectives may be affected by land use or climate changes, and if significant, the drought policy may need to be adjusted accordingly in the future. However, a trade-off between reservoir power generation and water release variability will always exist, which can be used to inform drought policy design, and the linear feature of the drought policy makes it relatively easy to adjust. It is very important to connect the characteristics of a water sharing policy with the trade-off between reservoir storage and releases. In this study, greater variability in releases leads to a steeper gradient of the drought policy line. These types of drought policy characteristics can provide guidance for stakeholders to effectively adjust the water sharing policy. Thus, the interpretable drought policy proposed here can enhance the understanding of water sharing and promote multi-lateral negotiations between upstream and downstream countries.
This framework here is based on annual flows; however, seasonal-scale and monthly operations could be of primary importance in smaller basins or for smaller-capacity reservoirs. Also, many other objectives and constraints, including firm power output, agricultural water supply reliability, and ecosystem functions, could be considered. Future research could explore drought-focused water sharing policies guiding reservoir operations across multiple timescales simultaneously and the application of seasonal-to-subseasonal inflow forecasts.

Figure A1Pareto front for maximum firm output (90 % guarantee) and minimum annual water release variance.

Figure A2Kernel distribution of annual reservoir inflow (Qin) and water release (Qout) under different power generation levels (1965–2017). Vertical lines represent the 10 % exceedance value.
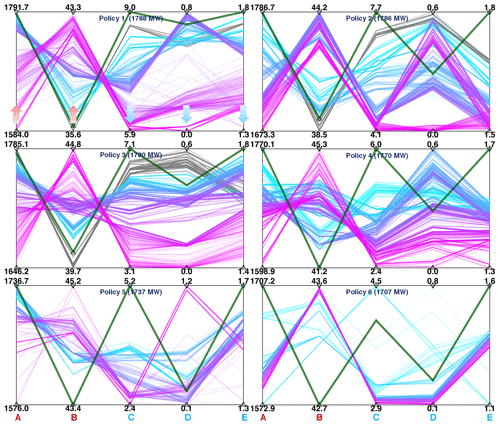
Figure A3Parallel plots of multiple objectives (A – mean output, MW; B – 10th percentile of annual water release, BCM; C – standard deviation in annual water release, BCM; D – spillage loss, BCM per year; E – evaporation loss, BCM per year) of each policy corresponding to the Pareto fronts in Fig. 9. The bold green line refers to the reservoir operation without the drought policy.
Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.
GY developed the model code, performed the simulations and visualizations, and prepared the original draft. PB conceptualized the idea, performed the data curation, and wrote, reviewed, and edited the paper.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We gratefully acknowledge Michael J. Tumbare, John Ndiritu, and two additional anonymous referees, whose numerous and detailed comments and recommendations helped improve the paper.
This research has been supported by the National Science Foundation (grant no. 1639214).
This paper was edited by Dominic Mazvimavi and reviewed by Michael J. Tumbare, John Ndiritu, and two anonymous referees.
Acharya, V., Halanaik, B., Ramaprasad, A., Swamy, T. K., Singai, C. B., and Syn, T.: Transboundary sharing of river water: Informating the policies, River Res. Appl., 36, 161–170, 2020.
Anghileri, D., Castelletti, A., Pianosi, F., Soncini-Sessa, R., and Weber, E.: Optimizing watershed management by coordinated operation of storing facilities, J. Water Res. Plan. Man., 139, 492–500, 2013.
Arjoon, D., Tilmant, A., and Herrmann, M.: Sharing water and benefits in transboundary river basins, Hydrol. Earth Syst. Sci., 20, 2135–2150, https://doi.org/10.5194/hess-20-2135-2016, 2016.
Asadzadeh, M. and Tolson, B. A.: Pareto archived dynamically dimensioned search with hypervolume-based selection for multi-objective optimization, Eng. Optimiz., 45, 1489–1509, 2013.
Bhaskar, N. R. and Whitlatch Jr., E. E.: Derivation of monthly reservoir release policies, Water Resour. Res., 16, 987–993, 1980.
Buşoniu, L., Ernst, D., De Schutter, B., and Babuška, R.: Cross-entropy optimization of control policies with adaptive basis functions, IEEE T. Syst. Man Cy. B, 41, 196–209, 2011.
Cancelliere, A., Giuliano, G., Ancarani, A., and Rossi, G.: A neural networks approach for deriving irrigation reservoir operating rules, Water Resour. Manag., 16, 71–88, 2002.
Chang, L. C. and Chang, F. J.: Intelligent control for modelling of real time reservoir operation, Hydrol. Process., 15, 1621–1634, 2001.
Chaves, P. and Chang, F.-J.: Intelligent reservoir operation system based on evolving artificial neural networks, Adv. Water Resour., 31, 926–936, 2008.
Conway, D.: The climate and hydrology of the Upper Blue Nile River, Geogr. J., 166, 49–62, 2000.
Degefu, D. M., He, W., Yuan, L., and Zhao, J. H.: Water allocation in transboundary river basins under water scarcity: a cooperative bargaining approach, Water Resour. Manag., 30, 4451–4466, 2016.
Dombrowsky, I.: Revisiting the potential for benefit sharing in the management of trans-boundary rivers, Water Policy, 11, 125–140, 2009.
Draper, S. E.: Sharing water in times of scarcity: Guidelines and procedures in the development of effective agreements to share water across political boundaries, ASCE, Reston, Virginia, USA, 2006.
Ezega News: Ethiopia dismisses reports of capacity reduction of GERD, available at: https://www.ezega.com/News/NewsDetails/7321/Ethiopia-Dismisses-Reports-of-Capacity-Reduction-of-GERD (last access: 19 April 2021), 2019a.
Ezega News: Power generation capacity of GERD slashed to 5150 MW – Ethiopian Minister, available at: https://www.ezega.com/News/NewsDetails/7331/Power-Generation-Capacity-of-GERD-Slashed-to-5150MW-Ethiopian-Minister (last access: 19 April 2021), 2019b.
Feng, Z. K., Niu, W. J., and Cheng, C. T.: Optimization of hydropower reservoirs operation balancing generation benefit and ecological requirement with parallel multi-objective genetic algorithm, Energy, 153, 706–718, 2018.
Gaudard, L., Romerio, F., Dalla Valle, F., Gorret, R., Maran, S., Ravazzani, G., Stoffel, M., and Volonterio, M.: Climate change impacts on hydropower in the Swiss and Italian Alps, Sci. Total Environ., 493, 1211–1221, 2014.
Giuliani, M., Herman, J., Castelletti, A., and Reed, P.: Many-objective reservoir policy identification and refinement to reduce policy inertia and myopia in water management, Water Resour. Res., 50, 3355–3377, 2014.
Giuliani, M., Castelletti, A., Pianosi, F., Mason, E., and Reed, P. M.: Curses, tradeoffs, and scalable management: Advancing evolutionary multiobjective direct policy search to improve water reservoir operations, J. Water Res. Plan. Man., 142, 04015050, https://doi.org/10.1061/(ASCE)WR.1943-5452.0000570, 2015a.
Giuliani, M., Pianosi, F., and Castelletti, A.: Making the most of data: an information selection and assessment framework to improve water systems operations, Water Resour. Res., 51, 9073–9093, 2015b.
Goor, Q., Halleux, C., Mohamed, Y., and Tilmant, A.: Optimal operation of a multipurpose multireservoir system in the Eastern Nile River Basin, Hydrol. Earth Syst. Sci., 14, 1895–1908, https://doi.org/10.5194/hess-14-1895-2010, 2010.
Government of Ethiopia: Vol. S/2020/409, United Nations Security Council, United Nations Digital Library, NY 10017, USA, 2020.
Guariso, G. and Whittington, D.: Implications of Ethiopian water development for Egypt and Sudan, Int. J. Water Resour. D., 3, 105–114, 1987.
Herman, J. D. and Giuliani, M.: Policy tree optimization for threshold-based water resources management over multiple timescales, Environ. Modell. Softw., 99, 39–51, 2018.
Jameel, A. L.: The Grand Ethiopian Renaissance Dam: An Opportunity for Collaboration and Shared Benefits in the Eastern Nile Basin, World Water and Food Security Lab, Amicus Brief, 1–17, World Water and Food Security Lab, Massachusetts Institute of Technology, Cambridge, MA 02139, USA, 2014.
Jeuland, M., Baker, J., Bartlett, R., and Lacombe, G.: The costs of uncoordinated infrastructure management in multi-reservoir river basins, Environ. Res. Lett., 9, 105006, https://doi.org/10.1088/1748-9326/9/10/105006, 2014.
Karamouz, M. and Houck, M. H.: Annual and monthly reservoir operating rules generated by deterministic optimization, Water Resour. Res., 18, 1337–1344, 1982.
Le Ngo, L., Madsen, H., and Rosbjerg, D.: Simulation and optimisation modelling approach for operation of the Hoa Binh reservoir, Vietnam, J. Hydrol., 336, 269–281, 2007.
Li, D., Zhao, J., and Govindaraju, R. S.: Water benefits sharing under transboundary cooperation in the Lancang-Mekong River Basin, J. Hydrol., 577, 123989, https://doi.org/10.1016/j.jhydrol.2019.123989, 2019.
Link, P. M., Scheffran, J., and Ide, T.: Conflict and cooperation in the water – nexus: a global comparative analysis of river basins under climate change, WIRES Water, 3, 495–515, 2016.
Luchner, J., Riegels, N. D., and Bauer-Gottwein, P.: Benefits of cooperation in transnational water-energy systems, J. Water Res. Plan. Man., 145, 05019007, https://doi.org/10.1061/(ASCE)WR.1943-5452.0001047, 2019.
McCormick, Z. L.: Interstate water allocation compacts in the western United States – some suggestions, J. Am. Water Resour. As., 30, 385–395, 1994.
McCracken, M. and Wolf, A. T.: Updating the Register of International River Basins of the world, Int. J. Water Resor. D., 35, 732–782, 2019.
Nile Basin Initiative: State of the River Nile basin, Nile Basin Initiative Secretariat, Entebbe, Uganda, 2012.
Nile Basin Initiative: Estimated and projected total population in Nile Basin Countries, in: Nile Basin Water Resources Atlas, Nile Basin Initiative Secretariat, Entebbe, Uganda, 2017.
Oliveira, R. and Loucks, D. P.: Operating rules for multireservoir systems, Water Resour. Res., 33, 839–852, 1997.
Paisley, R. K. and Henshaw, T. W.: Transboundary governance of the Nile River Basin: Past, present and future, Environmental Development, 7, 59–71, 2013.
Rani, D. and Moreira, M. M.: Simulation–optimization modeling: a survey and potential application in reservoir systems operation, Water Resour. Manag., 24, 1107–1138, 2010.
Reddy, M. J. and Nagesh Kumar, D.: Multi-objective particle swarm optimization for generating optimal trade-offs in reservoir operation, Hydrol. Process., 21, 2897–2909, 2007.
Revelle, C., Joeres, E., and Kirby, W.: The linear decision rule in reservoir management and design: 1, Development of the stochastic model, Water Resour. Res., 5, 767–777, 1969.
Sadoff, C. W. and Grey, D.: Beyond the river: the benefits of cooperation on international rivers, Water Policy, 4, 389–403, 2002.
Swain, A.: Challenges for water sharing in the Nile basin: changing geo-politics and changing climate, Hydrolog. Sci. J., 56, 687–702, 2011.
Tan, C. C., Erfani, T., and Erfani, R.: Water for energy and food: A system modelling approach for Blue Nile River basin, Environments, 4, 1–13, https://doi.org/10.3390/environments4010015, 2017.
Teasley, R. L. and McKinney, D. C.: Calculating the benefits of transboundary river basin cooperation: Syr Darya Basin, J. Water Res. Plan. Man., 137, 481–490, 2011.
Tesfa, B.: Benefit of grand Ethiopian renaissance dam project (GERDP) for Sudan and Egypt, EIPSA Communicating Article: Energy, Water, Environment & Economic, 1, 1–12, 2013.
Tikk, D., Kóczy, L. T., and Gedeon, T. D.: A survey on universal approximation and its limits in soft computing techniques, Int. J. Approx. Reason., 33, 185–202, 2003.
Tilmant, A. and Kinzelbach, W.: The cost of noncooperation in international river basins, Water Resour. Res., 48, W01503, https://doi.org/10.1029/2011WR011034, 2012.
Uitto, J. I. and Duda, A. M.: Management of transboundary water resources: lessons from international cooperation for conflict prevention, Geogr. J., 168, 365–378, 2002.
Vörösmarty, C. J., Green, P., Salisbury, J., and Lammers, R. B.: Global water resources: vulnerability from climate change and population growth, Science, 289, 284–288, 2000.
Wei, C. C. and Hsu, N. S.: Derived operating rules for a reservoir operation system: Comparison of decision trees, neural decision trees and fuzzy decision trees, Water Resour. Res., 44, W02428, https://doi.org/10.1029/2006WR005792, 2008.
Wheeler, K. G., Basheer, M., Mekonnen, Z. T., Eltoum, S. O., Mersha, A., Abdo, G. M., Zagona, E. A., Hall, J. W., and Dadson, S. J.: Cooperative filling approaches for the grand Ethiopian renaissance dam, Water Int., 41, 611–634, 2016.
Wheeler, K. G., Hall, J. W., Abdo, G. M., Dadson, S. J., Kasprzyk, J. R., Smith, R., and Zagona, E. A.: Exploring cooperative transboundary river management strategies for the Eastern Nile Basin, Water Resour. Res., 54, 9224–9254, 2018.
Wu, X. and Whittington, D.: Incentive compatibility and conflict resolution in international river basins: A case study of the Nile Basin, Water Resour. Res., 42, W02417, https://doi.org/10.1029/2005WR004238, 2006.
WWAP: The United Nations world water development report 2019: leaving no one behind, The United Nations world water development report 2019: leaving no one behind, UNESCO, Paris, France, 2019.
Yang, G., Guo, S., Li, L., Hong, X., and Wang, L.: Multi-objective operating rules for Danjiangkou reservoir under climate change, Water Resour. Manag., 30, 1183–1202, 2016.
Yang, G., Guo, S., Liu, P., and Block, P.: Integration and evaluation of forecast-informed multi-objective reservoir operations, J. Water Res. Plan. Man., 146, 04020038, https://doi.org/10.1061/(ASCE)WR.1943-5452.0001229, 2020.
Yang, G., Zaitchik, B., Badr, H., and Block, P.: A Bayesian adaptive reservoir operation framework incorporating streamflow non-stationarity, J. Hydrol., 594, 125959, https://doi.org/10.1016/j.jhydrol.2021.125959, 2021.
Zeitoun, M. and Mirumachi, N.: Transboundary water interaction I: Reconsidering conflict and cooperation, Int. Environ. Agreem.-P., 8, 297, https://doi.org/10.1007/s10784-008-9083-5, 2008.
Zelalem, Z.: Ethiopia and Egypt are pushing each other to the brink in a battle for control on the river Nile, Quartz Africa, available at: https://qz.com/africa/1862962/ethiopia-egypt-battle-for-river-nile-grand-dam-without-trump/ (last access: 19 April 2021), 2020.