Technical note: Accounting for snow in the estimation of root zone water storage capacity from precipitation and evapotranspiration fluxes

A common parameter in hydrological modeling frameworks is root zone water storage capacity (S_R[L]), which mediates plant water availability during dry periods as well as the partitioning of rainfall between runoff and evapotranspiration. Recently, a simple flux-tracking-based approach was introduced to estimate the value of S_R (Wang-Erlandsson et al., 2016). Here, we build upon this original method, which we argue may overestimate S_R in snow-dominated catchments due to snow melt and evaporation processes. We propose a simple extension to the method presented by Wang-Erlandsson et al. (2016) and show that the approach provides a lower estimate of S_R in snow-dominated watersheds. This S_R dataset is available at a 1 km resolution for the continental USA, along with the full analysis code, on the Google Colab and Earth Engine platforms. We highlight differences between the original and new methods across the rain–snow transition in the Southern Sierra Nevada, California, USA. As climate warms and precipitation increasingly arrives as rain instead of snow, the subsurface may be an increasingly important reservoir for storing plant-available water between wet and dry seasons; therefore, improved estimates of S_R will better clarify the future role of the subsurface as a storage reservoir that can sustain forests during seasonal dry periods and episodic drought.

1 Introduction

Root zone water storage capacity (S_R[L]) quantifies the maximum amount of subsurface water that can be stored for use by vegetation. This ecohydrological parameter plays a central role in the determination of plant community composition and drought resilience (Hahm et al., 2019a, b), runoff generation mechanisms (Botter et al., 2007; Salve et al., 2012), landslide triggering (Montgomery and Dietrich, 1994), landscape evolution (Deal et al., 2018), and the partitioning of precipitation into evapotranspiration and runoff (Porporato et al., 2004). Practically, in situ measurement of S_R at large spatial scales is infeasible, leading to the development of various methods for estimating S_R using remote sensing and model inversion approaches (de Boer-Euser et al., 2016; Gao et al., 2014; Wang-Erlandsson et al., 2016; Dralle et al., 2020a). Although high-resolution maps of soil plant-available water storage capacity exist (Reynolds et al., 2000), such maps incompletely describe the water used by plants. This may be because plants are unable to access the full reported depth of the soil column or because plants access water stored at depths below soil (Dawson et al., 2020; Schwinning, 2010). For example, roots can extend into and draw water from the bedrock vadose zone (rock moisture; sensu Rempe and Dietrich, 2018; Hahm et al., 2020) or groundwater (Miller et al., 2010; Lewis and Burgy, 1964). Within seasonally dry environments in particular, a significant volume of water accessed during the growing season can be derived from depths below mapped soils (Rose et al., 2003; Jones and Graham, 1993; Arkley, 1981). We emphasize that an accurate representation of S_R should therefore include not only moisture available within the soil but also plant-accessible water below the soil, which may include unsaturated moisture in weathered rock or groundwater.

S_R does not, however, include the snowpack, which is an aboveground water storage reservoir. Correctly estimating S_R in systems that currently receive a significant proportion of their precipitation as snow is particularly important given the ongoing shift from snow to rain under a warming climate (e.g., Knowles et al., 2006), and the attendant heightened significance of subsurface water storage dynamics to plant ecosystems and streams. An existing, widely used method for estimating S_R (Wang-Erlandsson et al., 2016) does not account for snowpack, which we show may result in an overestimation of S_R. Here, we present an extension to the original method to account for snow in calculating S_R. We describe the method details and highlight results from a rain–snow transition transect in the Southern Sierra Nevada, California, USA. We also provide a geoTIFF raster map of S_R across the continental USA at the 1 km pixel scale. Finally, we link to a Google Earth Engine (https://earthengine.google.com/, last access: 25 May 2021) script written in Python (https://www.python.org/, last access: 25 May 2021) within the Colab coding environment (https://colab.research.google.com/, last access: 25 May 2021) to document the application of the method as well as to facilitate comparative analyses using other widely available and spatially distributed precipitation, snow cover, and actual evapotranspiration datasets.

2 Method

To estimate S_R, Wang-Erlandsson et al. (2016) compute a running root zone storage deficit (more positive means larger capacity in the subsurface for moisture storage) using differences between fluxes exiting (F_out) and entering (F_in) the root zone during a given time interval (typically equal to the sampling period of the remotely sensed evapotranspiration dataset). Typically, F_in and F_out are set equal to precipitation (P) and evapotranspiration (ET), respectively. However, to obtain a robust lower-bound estimate of S_R, it is important to make sure that F_in is not underestimated (when in doubt, assume all precipitation enters the rooting zone) and that F_out is not overestimated (when in doubt regarding the amount of F_out that contributes to increases in the root zone storage deficit, simply set F_out=0). This is a general strategy also employed by Wang-Erlandsson et al. (2016). In particular, the method occasionally enforces zero values for F_out and F_in to ensure that deficit calculations are not overestimated in light of uncertainty in the timing or magnitude of fluxes; this is not equivalent to assuming that these fluxes are zero. For example, Wang-Erlandsson et al. (2016) set runoff and leakage fluxes from the root zone to zero – not because runoff and leakage do not occur but because the magnitude and timing of these fluxes are difficult to estimate with remotely sensed data products.

The original storage deficit tracking (and subsequent estimation of S_R) procedure presented by Wang-Erlandsson et al. (2016) is achieved through two steps. First, over a given time interval t_n to t_n+1, the accumulated difference ($A_{t_n\to t_{n+\mathrm{1}}}$) between F_out and F_in is calculated as

$$\begin{array}{}\text{(1)}& A_{t_n\to t_{n+\mathrm{1}}}=\underset{t_n}{\overset{t_{n+\mathrm{1}}}{\int }}{F}_{\mathrm{out}}-F_{\mathrm{in}}\mathrm{d}t.\end{array}$$

Here, as the root zone storage deficit is being calculated (and not actual storage), the incoming and outgoing fluxes have opposite signs from a conventional mass balance (outgoing fluxes minus incoming fluxes for deficit calculations, as opposed to incoming fluxes minus outgoing fluxes for storage). A lower bound on the root zone storage deficit at each time interval can then be calculated as the maximum value of zero and the running sum of these accumulated differences:

$$\begin{array}{}\text{(2)}& D\left(t_{n+\mathrm{1}}\right)=\max \left(\mathrm{0},D\left(t_n\right)+A_{t_n\to t_{n+\mathrm{1}}}\right).\end{array}$$

Finally, S_R is estimated as the maximum observed value of D.

The potential inaccuracies introduced by this original method that we explore here are that, during periods when snowpack is present within the pixel, F_in may be nonzero due to melting snow entering the rooting zone, for example, or F_out from the root zone may be overestimated (due to attribution of sublimation or evaporation from the snow surface to a flux from the subsurface). As discussed above, both of these possibilities may lead to an overestimation of S_R.

In the absence of spatially and temporally resolved information about snowmelt and sublimation dynamics, a simple way to correct for these potential errors is to continue to decrease the storage deficit as incoming precipitation arrives and to set F_out=0 during periods when snow cover (C, the fraction of the pixel covered in snow, which is reliably measured at large spatial scales via satellites) is present, thereby not counting evapotranspiration towards increasing the storage deficit during snowy periods. Thus, we introduce a correction term for the outgoing flux in the calculation of the accumulated difference between outgoing and incoming fluxes during each time interval:

$$\begin{array}{}\text{(3)}& A_{t_n\to t_n+\mathrm{1}}=\underset{t_n}{\overset{t_{n+\mathrm{1}}}{\int }}\left(\mathrm{1}-⌈C-C_{\mathrm{0}}⌉\right)\cdot F_{\mathrm{out}}-F_{\mathrm{in}}\mathrm{d}t,\end{array}$$

where C₀ is some threshold below which it is assumed that snow cover is negligible, and ⌈⋅⌉ is the ceiling operator (rounding up to the nearest integer), returning a 1 if C>C₀ and 0 if C≤C₀. Therefore, the expression effectively sets F_out=0 whenever snow is present (or deemed not negligible) in the pixel, providing a lower-bound estimate of S_R in the running storage deficit calculation.

2.1 Algorithm implementation and datasets

We implement the original and snow-corrected algorithm developed here using Google Earth Engine, accessed via a Google Colab notebook and the Python programming language's Earth Engine application programming interface. This readily enables (i) access to distributed time series of hydrological products (i.e., snow cover, evapotranspiration, and precipitation); (ii) computation in the cloud; and (iii) a shareable script that can be quickly modified and executed by new users (see link at the end of the paper).

The algorithm requires precipitation and evapotranspiration datasets to compute F_in and F_out as well as a snow cover dataset to implement the proposed snow-correction step. We use Oregon State's PRISM (Parameter-elevation Regressions on Independent Slopes Model) daily precipitation product (https://developers.google.com/earth-engine/datasets/catalog/OREGONSTATE_PRISM_AN81d, last access: 25 May 2021) (Daly et al., 2008, 2015), available at a 2.5 arcmin resolution. For evapotranspiration, we use the cloud-corrected Penman–Monteith–Leuning Evapotranspiration V2 product (https://developers.google.com/earth-engine/datasets/catalog/CAS_IGSNRR_PML_V2, last access: 25 May 2021) (Zhang et al., 2019; Gan et al., 2018), available at an 8 d time step and 500 m resolution, and sum the vegetation transpiration, interception, and soil evaporation bands to calculate total evapotranspiration. For the snow cover dataset, we use the normalized difference snow index (NDSI) snow cover band from the 500 m MODIS/Terra data product (https://developers.google.com/earth-engine/datasets/catalog/MODIS_006_MOD10A1, last access: 25 May 2021) (Hall et al., 2016) and set C₀=0.1 (snow cover is assumed negligible at less than C₀=10% pixel coverage; in this case, C₀=10 % is also the minimum nonzero value of the underlying snow cover dataset). We restrict our analysis to the temporal intersection of these three datasets (the root zone storage deficit is tracked continuously from the 2003 to the 2017 water year), reproject into WGS84 (EPSG:4326), and resample pixels using nearest-neighbor sampling to a 32.34 arcsec pixel scale (approximately 1 km).

We mask out pixels from our analysis where we anticipate our method will fail to accurately estimate S_R, namely urban areas, open water, and croplands (which are typically subject to irrigation). To generate this mask, we use the “LC_Type1” band from the 2001 year of the MODIS MCD12Q1 v6 land cover product (https://developers.google.com/earth-engine/datasets/catalog/MODIS_006_MCD12Q1, last access: 25 May 2021) (Friedl and Sulla-Menashe, 2015). In some areas (e.g., deserts), dataset errors or unaccounted for inter-pixel flow result in unrealistic S_R estimates, as described by Wang-Erlandsson et al. (2016). In the case that inter-pixel flow results in a net contribution to the root zone, estimates of S_R in our (and the original) method may not represent true lower bounds. At present, however, there are few if any methods for reliably measuring such inter-pixel fluxes at large scales, let alone for determining whether vegetation has access to these fluxes. Wang-Erlandsson et al. (2016) suggest a potential correction technique for this issue by adding the long-term average difference ET–P (where it is positive) to F_in. However, we choose to remove these areas entirely from our data product by masking out pixels where cumulative evapotranspiration over the study period exceeds cumulative precipitation. If needed, this correction method implemented by Wang-Erlandsson et al. (2016) can easily be added to the code notebook published alongside this paper.

Finally, to provide an example of the impact of the method, we focus on the western slope of the Sierra Nevada in California, USA, where elevations range from approximately 100 to 4000 m, driving strong gradients in mean annual temperature (−1.5 to 17.5 ^∘C; PRISM Climate Group, 2017), mean annual precipitation (120 to 1500 mm; PRISM Climate Group, 2017), vegetation cover (oak savanna at low elevations to mixed conifer forest at high elevations), and annual maximum snow cover (0 % to 100 %).

3 Results

Figure 1 illustrates three raster data layers in the Sierra Nevada focus region derived from the application of the new method. Figure 1a plots root zone storage capacity calculated using the snow-correction method. Values range from near 0 mm over exposed bedrock outcrops in the High Sierra, to over 900 mm in the dense mid-elevation forests. Figure 1b shows the difference between S_R computed using the original method and the snow-corrected S_R. Figure 1c plots average winter (January–April) snow cover. As expected, the difference in Fig. 1b is small in the lower, rain-dominated elevations, and larger in areas with snow cover. However, some areas with substantial snow cover show small differences between the methods. These are likely areas where root zone storage capacity is small, coinciding with exposed-bedrock locations at high elevations.

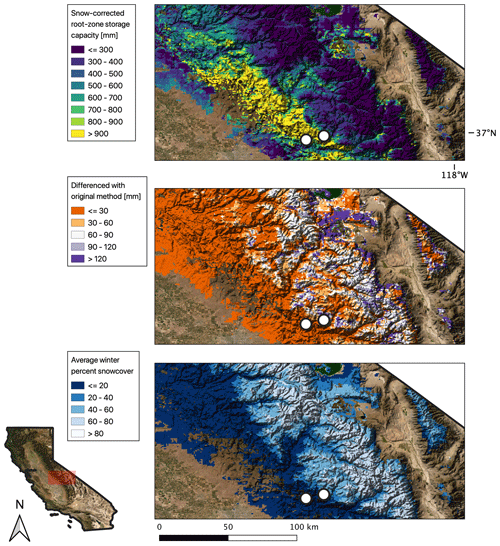
Figure 1 Maps of snow-corrected S_R (a), the difference between the original and snow-corrected S_R (b), and average winter (January–April) percent snow cover (c) over a region of the Southern Sierra Nevada, California, USA. White points identify rain-dominated (western) and snowy (eastern) locations highlighted in Fig. 2. Imagery was obtained from publicly available data through the US Department of Agriculture, Farm Service Agency's National Agriculture Imagery Program.

Figure 2 illustrates the full time series output of the snow-accounting and original methods at two locations, identified by white points in Fig. 1. The location farther west is a “low-snow” location, with negligible snowfall (snow present less than 1 % of the time) during the winter months, and the location to the east is a “high-snow” location, with snow cover present over 50 % of the time during the winter months. Gray shading in all subplots indicates that more than 10 % of the pixel is covered in snow at that time point, during which evapotranspiration is set to zero in our method (panels c and d). Figure 2a and b plot storage deficits using the original and the snow-accounting methods, clearly demonstrating the divergence of deficit calculations between the two methods in the region with significant snow cover. In all instances, S_R is calculated as the maximum observed value of the storage deficit. In the high-snow location using the original method, this leads to an estimated value of S_R that is approximately 50 % larger than that calculated with the snow-accounting method.

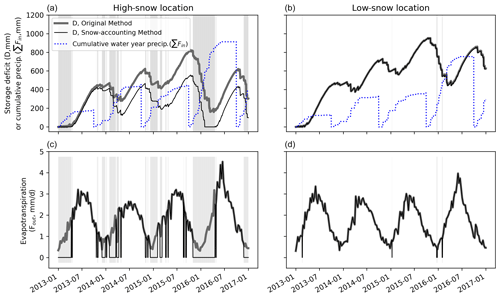
Figure 2 Storage deficit time series for representative “high-snow” and “low-snow” locations in the Sierra Nevada (locations mapped in Fig. 1) from 2013 through 2016, showing the difference between the original and snow-accounting methods. Cumulative water year precipitation (instantaneous precipitation is F_in) is plotted in dotted blue in panels (a) and (b), and ET (F_out) is plotted in panels (c) and (d), where the snow-accounting method takes F_out=0 during periods of snow cover (gray shading in background). During snow-free periods (white background), deficits change identically (though there may be a vertical offset). During periods when snow is present, the new method prevents deficit growth, whereas the deficit may grow during snowy periods using the original method (e.g., January 2015). The plot demonstrates how the original method may lead to a larger estimate of S_R (computed as the maximum value of D) in snow-dominated locations.

4 Discussion

Our proposed method for estimating S_R provides a minimum estimate. Actual S_R should generally exceed estimated S_R values presented in our revised method, because some evapotranspiration occurs during times when snow cover is present. The snow-accounting method and the original method do not account for leakage, surface runoff, and upslope drainage in the calculation of F_in.

Drawbacks associated with the general approach are presented in detail in Wang-Erlandsson et al. (2016). In particular, the results are highly sensitive to the quality of the underlying remote sensing datasets; by making our code publicly available, we hope that improved datasets can be readily incorporated as they become available on order to produce better estimates of S_R. As noted in a similar effort by Dralle et al. (2020a), we caution against using evapotranspiration datasets that rely on a soil water balance as a model parameter, which incorporate predetermined values of S_R (e.g., from existing soils databases), as this would bias the inferred S_R.

Because the method relies on a mass balance approach, estimates of S_R will inherently be larger in locations where rates of plant water use are high during extended dry periods; for example, in the Mediterranean-type climate of California, where the long dry summer coincides with the growing season. Consequently, S_R estimates will be less representative of the potentially observable maximum of root zone water storage capacity in wetter climates because root zone storage deficits are frequently replenished and, therefore, never reach large values. In other words, this method is only capable of documenting the root zone storage capacity that is accessed by plants, rather than the accessible plant-available water storing capacity that may exist through the whole rooting zone (sensu Klos et al., 2018); the former provides a minimum estimate of the latter. In energy-limited environments or places where seasonal precipitation and energy delivery are in phase, the method is prone to a significant underestimation of plant-accessible water.

S_R in rain-dominated climates has been shown to impact drought resilience (Hahm et al., 2019a), and snow–rain transition elevations are increasing as the climate warms (Knowles et al., 2006). If precipitation arrives as rain rather than snow, the role of the subsurface in storing that water for plants will likely be amplified. Mountainous snow–rain transition zones can support high rates of ET and coincide with forested areas (Goulden et al., 2012; Hahm et al., 2014), underscoring the importance of accurate estimates of S_R for prediction of forest sensitivity to climate variability in the future.

Finally, we caution that neither this dataset nor the original dataset calculated by Wang-Erlandsson et al. (2016) have been validated against direct measurements of root zone storage capacity. Although Wang-Erlandsson et al. (2016) performed an implicit validation of S_R via hydrological modeling, we advocate for complementary in situ measurements of dynamic water storage in the critical zone, which will be required for true validation of emerging remote sensing datasets of subsurface water storage (e.g., Wang-Erlandsson et al., 2016; Enzminger et al., 2019; Swenson et al., 2003). Systematic validation of this form requires significant new fieldwork efforts that we leave for future work.

5 Conclusions

We argue that an existing method for estimating root zone water storage capacity (S_R) will tend to overestimate S_R in snowy areas due to unaccounted for snow melt, evaporation, and sublimation processes. We provide a correction factor that relies on a widely available distributed percent snow cover dataset to provide a tighter lower-bound estimate on S_R. Accurately describing S_R is important because the role of the subsurface in storing water is likely to be amplified in a warming climate, in which more precipitation will fall as rain rather than snow.