Unsaturated zone model complexity for the assimilation of evapotranspiration rates in groundwater modelling

The biophysical processes occurring in the unsaturated zone have a direct impact on the water table dynamics. Representing these processes through the application of unsaturated zone models of different complexity has an impact on the estimates of the volumes of water flowing between the unsaturated zone and the aquifer. These fluxes, known as net recharge, are often used as the shared variable that couples unsaturated to groundwater models. However, as recharge estimates are always affected by a degree of uncertainty, model–data fusion methods, such as data assimilation, can be used to inform these coupled models and reduce uncertainty. This study assesses the effect of unsaturated zone models complexity (conceptual versus physically based) to update groundwater model outputs, through the assimilation of actual evapotranspiration rates, for a water-limited site in South Australia. Actual evapotranspiration rates are assimilated because they have been shown to be related to the water table dynamics and thus form the link between remote sensing data and the deeper parts of the soil profile. Results have been quantified using standard metrics, such as the root mean square error and Pearson correlation coefficient, and reinforced by calculating the continuous ranked probability score, which is specifically designed to determine a more representative error in stochastic models. It has been found that, once properly calibrated to reproduce the actual evapotranspiration–water table dynamics, a simple conceptual model may be sufficient for this purpose; thus using one configuration over the other should be motivated by the specific purpose of the simulation and the information available.

1 Introduction

Actual evapotranspiration (AET) and groundwater recharge to the water table (WT) are two interrelated components of the water cycle. This is because AET is a function of the soil water content within the root zone, as the root water uptake is distributed along the entire root system (Grinevskii, 2011; Neumann and Cardon, 2012). Improving AET estimates, by means of a detailed modelling of the soil water transport, can enhance the simulation of net recharge (i.e. recharge to the WT minus transpiration from WT) and, in turn, WT dynamics. This is particularly important when the WT is within the reach of the roots, as is common in Australian semi-arid catchments (Banks et al., 2011) because the root water uptake from groundwater and the capillary fringe can largely contribute to AET (Mensforth et al., 1994; Orellana et al., 2012).

AET is often simulated through a variety of numerical models that reproduce the soil water–vegetation interaction with different level of details. Advanced integrated surface water–groundwater models (e.g. Hydrogeosphere, Therrien et al., 2006; CATHY, Camporese et al., 2010; PARFLOW, Jones and Woodward, 2001) or coupled saturated–unsaturated zone models (Facchi et al., 2004; Simunek et al., 2009; Zhu et al., 2012; Van Walsum and Veldhuizen, 2011; Grimaldi et al., 2015) are able to account for the direct groundwater–vegetation interaction. In general, the representation of the unsaturated zone is obtained from simple conceptual water balance models or detailed physically based models.

Conceptual unsaturated zone models (UZMs) simplify the processes occurring in the unsaturated zone and are widely used for spatially distributed hydrological simulations (Teuling and Troch, 2005). An example is Batelaan and De Smedt (2007), who successfully applied a coupled surface water–groundwater balance model at the regional scale, focusing on the assessment of net recharge rates. Conceptual water balance models have been found to be flexible as they usually require shorter run times and fewer parameters and are suitable when stochastic simulations based on Monte Carlo techniques are applied (Kim and Stricker, 1996; Fatichi et al., 2016). However, for more detailed simulations, such as in ecohydrology or agricultural modelling, simple UZMs may fail to accurately simulate important processes such as water stress or root growth (Krysanova and Arnold, 2008); thus physically based models are preferred. Commonly, physically based models solve the Richards equation for water flow in porous media, relying on relationships between soil volumetric water content, hydraulic conductivity, and soil water pressure head (van Dam et al., 2008; Scheerlinck et al., 2009). Physically based models thus have the ability to account for specific effects that affect the calculation of AET, such as capillary rise, thereby impacting net recharge estimates. The latter is particularly important when UZMs are coupled to saturated models as net recharge acts as the link between both models (Doble et al., 2017).

Given the spatial variability and number of parameters (e.g. the water retention curve and detailed vegetation characteristics) required by physically based models, their application, particularly in data-scarce areas, can be challenging (Simmons and Meyer, 2000). Conversely, conceptual models may require fewer input data, but, their recharge estimates may be less reliable. This occurs because they are affected by both structural uncertainty, induced by the simplification of the model (Renard et al., 2010), and the epistemic and aleatory uncertainty of the forcing inputs (Khatami et al., 2019). Accurate model parameters and meteorological inputs are far from always available, especially at large spatial scales. Therefore, the use of remote sensing data can provide vital information for these models (Entekhabi and Moghaddam, 2007; Carroll et al., 2015; Lu et al., 2020).

One way to make use of the remote sensing observations is through data assimilation, which combines model results with independent observations to reduce model uncertainty. In the field of hydrology, there is a plethora of studies on the assimilation of diverse observations such as soil moisture (SM), leaf area index, and streamflow and groundwater levels (Liu et al., 2012; Li et al., 2016). Satellite remote sensing data have been proven to be a valid alternative when field-based observations cannot provide sufficiently accurate measurements. Remotely sensed SM values are a function of the water content of the upper few centimetres of the soil (Pipunic et al., 2014). Consequently, models using remotely sensed SM assimilation extrapolate the update for the upper soil layer to the entire modelled soil column through the covariance between the upper and lower layer modelled SM values. On the other hand, remotely sensed AET rates are a function of the modelled water content of the soil column up to the rooting depth. In consideration of this, the assimilation of remotely sensed AET has the potential of directly updating the water content of the entire modelled soil column. In recent years, the assimilation of satellite-based AET observations has been recognised to be beneficial for the reduction of the uncertainty of several hydrogeological products (e.g. recharge and depth to WT), especially for data-scarce areas (Entekhabi and Moghaddam, 2007; Doble et al., 2017; Gelsinari et al., 2020).

All satellite observations present a trade-off between accuracy, time frequency, and spatial coverage. In addition, no satellite retrievals are free from errors, as discussed in Long et al. (2014), who analysed and compared the uncertainty in the AET estimates from different sources, including the Moderate-Resolution Imaging Spectroradiometer (MODIS). They concluded that AET derived from land surface models had a lower uncertainty than the MODIS-based AET (5 vs. 12.5 mm per month, respectively) and suggested a hybrid approach for taking advantage of the integration of land surface models and remotely sensed products. Droogers et al. (2010) applied an inverse modelling approach (i.e. forward–backwards optimisation) using a physically based UZM and found that improvements were obtained when the frequency of the AET observations was finer than a 15 d interval. It appears that, for the purpose of proficiently using AET retrievals, the assimilation framework should allow for frequent updates (<15 d interval) and account for observation errors. This was also synthetically shown by Gelsinari et al. (2020), who improved the model outputs, using the ensemble Kalman filter (EnKF) for the sequential assimilation of the averaged 8 d AET into a conceptual UZM coupled to MODFLOW (Harbaugh, 2005). The assimilation of satellite AET observations has been shown to be a feasible way to constrain hydrologic models; however, this has yet to be validated against experimental data. Furthermore, it is known that UZMs of different complexity can yield different AET estimates, producing distinct recharge values and, in turn, a diverse dynamics of the WT.

This study aims to perform the validation of the AET assimilation framework proposed in Gelsinari et al. (2020) and to assess the use of a conceptual and a physically based UZM within a data assimilation framework to improve WT estimates. The quantities of interest are the temporal WT fluctuation dynamics and the modelled actual AET. A conceptual and a physically based UZM are coupled to MODFLOW and applied to a water-limited study site in the south-east of South Australia. Remotely sensed AET observations are assimilated into both of these coupled models, and assessments of the improvements in the results of the model are made. Based on this assessment, a number of recommendations regarding the required UZM complexity to obtain a positive impact on the quantities of interest are made.

2 Methods

2.1 Study area and data

The study area is situated in the south-eastern part of South Australia, north of the city of Mount Gambier (Fig. 1a and b). This region has a Mediterranean climate with cool, wet winters and warm, dry summers. The climatic forcing inputs are rainfall and potential evapotranspiration (PET) obtained from the Bureau of Meteorology (BOM – station no. 26021). The historical data for this station report an average annual rainfall and PET of approximately 710 and 980 mm yr⁻¹, respectively, calculated over the period 1942–2017. The Morton equation (Donohue et al., 2010) and the Budyko curve (Donohue et al., 2007) classify the area as dominated by evapotranspiration or water-limited (Jackson et al., 2009; Benyon et al., 2006).

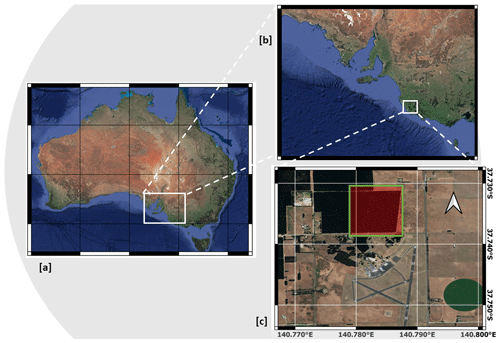
Figure 1 Localisation of the study area within Australia (a), the south-east of South Australia (b), and a detail of the forest plantation (c). The red square indicates the CMRSET tile. © Google Maps

The study site is a Pinus Radiata plantation next to Mount Gambier Airport (Fig. 1c). The trees were originally planted in July 1996 with a density of 1225 trees per hectare. The survey performed by Benyon et al. (2006) classified the soil as duplex. This type of soil presents a contrast between the upper part, which features sandy loam characteristics with high hydraulic conductivity, and the lower part, classified as clay, with a finer texture and lower hydraulic conductivity. The average WT depth, from the observations at one bore, is reported at approximately 6 m below the surface. SM observations were taken with a neutron probe, about every 4 weeks from August 2000 to January 2005, up to a depth of 3 m at an interval of 30 cm. In this region more than 90 % of the available groundwater is in shallow aquifers, and these plantations have been shown to have direct access to groundwater (Benyon and Doody, 2004).

AET data are derived from the remotely sensed CSIRO MODIS-reflectance-based scaling evapotranspiration (CMRSET) algorithm (Guerschman et al., 2009). These values are obtained by rescaling the PET rates calculated with the Penman–Monteith algorithm using the enhanced vegetation index and global vegetation moisture index obtained from MODIS (Swaffer et al., 2020). The observations are available every 8 d, with a spatial resolution of 250 by 250 m.

2.2 Model description

The tests presented in this study used two different configurations of coupled groundwater–unsaturated zone models, which are depicted in Fig. 2. The following sections describe the models as well as the coupling framework.

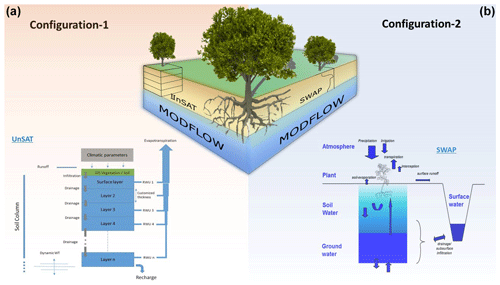
Figure 2 Coupled models' representation. (a) UnSAT conceptualisation coupled to MODFLOW. (b) SWAP conceptualisation coupled to MODFLOW.

2.2.1 UnSAT – UZM

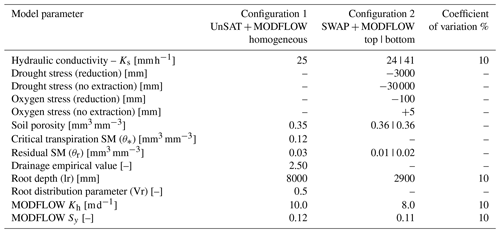
The UnSAT (Unsaturated zone and SATellite) UZM is a one-dimensional soil water balance model. The unsaturated zone is divided into layers, and the water balance of each layer is solved at every time step. Water flows downward from the top layer to the last, and the latter delivers recharge (Fig. 2). The model uses climate forcing data (i.e. precipitation [mm h⁻¹] and PET [mm h⁻¹]) on a raster-distributed basis as inputs and returns values of AET [mm h⁻¹], runoff [mm h⁻¹], recharge [mm h⁻¹], and soil water content (θ [mm³ mm⁻³]). The soil is parameterised using the porosity (θ_s), a critical soil water content to define water stress (θ_* [mm³ mm⁻³]), residual soil water content (θ_r [mm³ mm⁻³]) (as in Laio et al., 2001), hydraulic conductivity (K_s [mm³ mm⁻³]), and an empirical value for drainage (b [–]); the root system is defined using root depth (lr [mm]) and a root density distribution parameter (Vr [–]) (Vrugt et al., 2001a).

The size of the layers (Δz [mm]) remains constant, while their number changes according to the depth to WT, which is provided by the groundwater model. Along the soil profile, the model accounts for water extraction due to root water uptake. For each layer, the water balance equation is solved using an explicit finite difference approximation, solved with an hourly time step (Δt). The water balance of the layer at the soil surface is calculated as

$$\begin{array}{}\text{(1)}& {\mathit{\theta }}_{\mathrm{1}}^{t+\mathrm{1}}={\mathit{\theta }}_{\mathrm{1}}^t+{\displaystyle \frac{P^t-{\text{AET}}_{\mathrm{1}}^t-Q^t-D_{\mathrm{1}}^t}{\mathrm{\Delta }{z}_{\mathrm{1}}}}\cdot \mathrm{\Delta }t,\end{array}$$

where P is precipitation, Q is runoff and D is percolation. In Eq. (1), the subscripts 1 refer to the soil layer at the surface, and the superscripts refer to the time step. The percolation $D_{\mathrm{1}}^t$, which proceeds to the lower layer, is defined by the Clapp–Hornberger (Clapp and Hornberger, 1978) modification of the Brooks–Corey model.

AET is calculated as

$$\begin{array}{}\text{(2)}& \text{AET}=\text{PET}\cdot \mathit{\beta }\left(z\right)\cdot \mathit{\alpha }\left(\mathit{\theta }\right),\end{array}$$

where β(z) is the root distribution function as in Vrugt et al. (2001b), and α is a water stress reduction function (Laio et al., 2001; Feddes et al., 1976).

For the layers below the first, including the last layer, which delivers recharge to the groundwater model, the water balance equation is

$$\begin{array}{}\text{(3)}& {\mathit{\theta }}_n^{t+\mathrm{1}}={\mathit{\theta }}_n^t+{\displaystyle \frac{D_{n-\mathrm{1}}^t-({\text{AET}}_n^t+D_n^t)}{\mathrm{\Delta }{z}_n}}\cdot \mathrm{\Delta }t.\end{array}$$

For a more detailed description of the UnSAT model, see Gelsinari et al. (2020).

2.2.2 SWAP UZM

The Soil Water Atmosphere Plant (SWAP v. 4.0) model, developed by Alterra, is one of the most used physically based UZMs (van Dam et al., 2008; Kroes et al., 2017). This agro-hydrological model is able to simulate the water, heat, and solute flow in heterogeneous, variably saturated soils. Water flow is simulated using the Richards equation. In addition, it has the potential of accounting for a detailed soil water–vegetation interaction as it specifically simulates the dynamics of the crop growth cycle.

In SWAP, the Richards equation is solved for the pressure head using finite differences. The soil hydraulic retention functions are based on the analytical formulations proposed by van Genuchten (1980). The model requires the van Genuchten soil parameters and a number of vegetation-specific parameters (Feddes et al., 1976). In this study, the parameters accounting for the drought stress, which are the pressure head value below which water uptake reduction starts (i.e. −3000 mm) and the pressure head value triggering no further water extraction (i.e. −30 000 mm), are a result of the calibration. For this experiment, the standard forest root density distribution is applied.

2.2.3 Groundwater model

The groundwater model chosen for the study is MODFLOW 2005 (Harbaugh, 2005). This modular flexible model has packages dedicated to the calculation of evapotranspiration and the application of recharge to the groundwater. In this study, the evapotranspiration package of MODFLOW (EVT) was replaced with the UZMs (UnSAT and SWAP), and the recharge (RCH) package was used to apply the UZMs' calculated net recharge to the cell-specific head.

FloPy (Bakker et al., 2016), a library that allows MODFLOW to run in a Python environment, was used to generate the saturated model and to specify parameters. The model runs at an 8 d time step, which is considered adequate for WT dynamics. This choice was motivated by matching the temporal resolution of the CMRSET data.

2.2.4 Coupling

UZMs require a shorter time step than MODFLOW as the water content varies at a higher frequency than the depth to the WT in the groundwater model (Xu et al., 2012). Variation of the WT at regional scales usually can only be observed at temporal scales in the order of months or years. Thus, applying a larger time step for the saturated zone model is a valuable option to reduce the computational time (Facchi et al., 2004). At large spatial scales, dimensional simplification to 1D unsaturated zone flow simulations has been shown to be sound because the direction of the unsaturated zone flow is predominantly vertical (Zhu et al., 2011).

Configuration-1 (Fig. 2a) features the UnSAT model coupled to MODFLOW. This configuration specifically accounts for plant transpiration from the WT by calculating the balance between recharge entering the WT (positive) and transpiration (negative). UnSAT runs at an hourly time step, while MODFLOW runs with an 8 d time step, matching the MODIS time step. Once MODFLOW has performed the calculation of the WT levels, these are fed back on a raster basis to UnSAT, which uses them to recalculate the number of layers in which the unsaturated zone is discretised. This dynamic scheme, defined in Zeng et al. (2019) as the non-iterative feedback coupling method, is considered a valuable trade-off between the computational cost of fully coupled or iterative schemes and numerical accuracy.

For Configuration-2 (Fig. 2b), the unsaturated zone is simulated through the SWAP model, with the pressure head along the soil column as the state variable. The model has been coupled to MODFLOW through the recharge, similar to the coupling methodology reported by Xu et al. (2012). This type of coupling requires caution in the definition of the S_y parameter, which becomes part of the calibration and is discussed in the next section.

2.3 Model domain and calibration

The model configurations were applied to a domain of 1×5 cells of 1 km² each and a single vertical unconfined layer (Fig. 3). The domain discretisation was chosen as a result of a sensitivity analysis conducted on a range of model domains varying from fine (1×20 cells) to coarse (1×5 cells). The boundary cells were set to a constant head obtained via calibration (i.e. 3.5 m below the surface). The location chosen allows the model configuration to remain simple and to define constant head boundary conditions. This is due to the site being in the centre of a forestry block, more than 2 km from any groundwater extraction. For this region, where WT is 6 m deep or shallower, it has been shown that forestry transpiration from groundwater is around 2 orders of magnitude (i.e. 435 ML yr⁻¹ for a 1 km by 1 km fully forested cell) larger than the maximum groundwater extraction rate from a single bore (Benyon et al., 2006). To further reinforce the selection of constant head boundary conditions, an analysis of the WT fluctuations was conducted on bores in the proximity of the study area but outside of the forest. The analysis showed that, for a WT level of 4.4 m below the surface, the standard deviation was low (i.e. 0.12 m). This supports the assumption that, if higher WT table fluctuations are observed (such as the investigated location), these are dependent on the local net recharge.

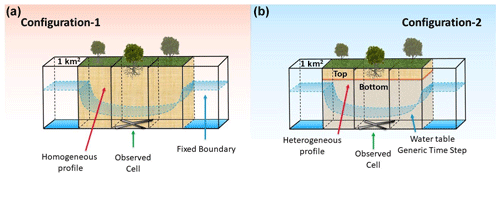
Figure 3 Schematic of the model domain. (a) Configuration-1 models the unsaturated zone as a homogeneous profile with UnSAT. (b) Configuration-2 models the soil heterogeneity by accounting for the change in soil properties with SWAP. The representation of WT levels refers to the generic simulation time and is conceptually showing the depression caused by the root water extraction.

UnSAT can account for the decrease of K_s along the soil column, whereas SWAP is capable of explicitly modelling the heterogeneity of the soil column, as described in Sect. 2.1. Thus, for Configuration-1, soil parameters are homogeneous along the soil column length (i.e. 10 m or 100 layers of 10 cm), while in Configuration-2, the first (upper) 1.5 m of soil is classified as sandy loam soil, and the second (lower) is a loam clay soil spanning the rest of the simulated soil column (i.e. 8.5 m).

In order for the system to be observable, the link between WT levels and AET has to be accurately reproduced. It should be noted that this link has been described in the literature (Shah et al., 2007; Xie et al., 2018; Zhang et al., 2020). To account for this interdependence, a multi-objective function (MOF), which combines WT depths and AET values, was introduced. Then, SM observations were used for refinement and to set boundaries to the soil parameters. The algorithm particle swarm optimisation (PSO) (Kennedy and Eberhart, 1995; Shi and Eberhart, 1998) was used for calibration, minimising the specifically defined MOF:

$$\begin{array}{}\text{(4)}& \text{MOF}={\displaystyle \frac{\text{RMSE}\left(\text{WT}\right)}{\mathit{\sigma }\left(\text{WT}\right)}}+{\displaystyle \frac{\text{RMSE}\left(\text{AET}\right)}{\mathit{\sigma }\left(\text{AET}\right)}},\end{array}$$

where RMSE is the root mean square error, and σ is standard deviation. The calibrated parameters are listed in Table 1.

Table 1 Calibrated parameter values used for the simulations and their coefficient of variation.

Applying a calibration–validation approach, the observation data sets were divided into two periods. For calibration, 46 time steps covering roughly the year 2001 were used, while the rest of the data set (4.5 years in total) was used for validation.

2.4 Assimilation

The EnKF (Evensen, 1994) was used because of its reduced computational burden when dealing with highly non-linear systems. The filter initially requires the generation of a number of ensemble members by perturbing the forcing inputs of precipitation and PET. After having tested other ensemble sample sizes (i.e. 16, 32, 64), the ensemble sample size was set to M=32, a size which has been widely used for a number of EnKF applications (Mitchell et al., 2002; Pauwels et al., 2013), and represented the best trade-off between computational time and accuracy for the case tested. To verify the spread and accuracy of the ensemble, statistical variables, such as the ensemble skill and ensemble spread, originally developed for numerical weather prediction by Talagrand et al. (1997), were calculated on the ensemble population (these are discussed in Sect. 2.4.1).

Usually, in data assimilation studies, the assimilated observations are model states (also called prognostic variables) such as SM, pressure head, and WT levels. This paper uses AET flux observations, which are diagnostic variables. Therefore, the interaction between AET and model states occurs in the UZM, of which AET is a model result. Following Gelsinari et al. (2020), AET data from the CMRSET are assimilated into the coupled model configurations.

The two configurations apply a similar scheme of the EnKF, the difference lying in the composition of the aggregated state vector, as the state variables of the UZMs are different. Specifically, the state vector of Configuration-1, for a single ensemble member ($i=\mathrm{1},\mathrm{\cdots },M$), is composed of the WT level h and a vector of the SM values at time step s, represented as

$$\begin{array}{}\text{(5)}& {\mathit{z}}_{[\mathbf{1}{]}_s}^{i,f}=\left[{\mathit{\theta }}_{\mathrm{1}}{\mathit{\theta }}_{\mathrm{2}}\mathrm{\cdots }{\mathit{\theta }}_n\right],\end{array}$$

where ${\mathit{\theta }}_{\mathrm{1}},{\mathit{\theta }}_{\mathrm{2}},\mathrm{\cdots },{\mathit{\theta }}_n$ are the values of SM content for each layer of the UZM, for the ith ensemble member, and f represents the forecast.

For Configuration-2, the vector of soil water pressure heads is

$$\begin{array}{}\text{(6)}& {\mathit{z}}_{[\mathbf{2}{]}_s}^{i,f}=\left[p_{\mathrm{1}}{p}_{\mathrm{2}}\mathrm{\cdots }{p}_n\right],\end{array}$$

where, for the ith ensemble member, $p_{\mathrm{1}},p_{\mathrm{2}},\mathrm{\cdots },p_n$ are the pressure head values for each layer of the UZM. The filter scheme is then similarly applied for both configurations as follows. Here, only the aggregated state vector of Configuration-1 (composed in the same fashion for both configurations) for the assimilation time step k and the ensemble member i is reported. This is

$$\begin{array}{}\text{(7)}& {\mathit{x}}_k^{i,f}=[h^{i,f},{\mathit{z}}_{[\mathrm{1}{]}_{\mathrm{1}}}^{i,f},{\mathit{z}}_{[\mathrm{1}{]}_{\mathrm{2}}}^{i,f},\mathrm{\cdots },{\mathit{z}}_{[\mathrm{1}{]}_t}^{i,f}{]}^T,\end{array}$$

where t is the number of times the UZM model is applied between two applications of the filter (i.e 8 d), T indicates the transposed vector, and h is the WT level, constant during the t time steps, simulated by MODFLOW.

The average state vector reads

$$\begin{array}{}\text{(8)}& {\stackrel{\mathrm{‾}}{\mathit{x}}}_k^f={\displaystyle \frac{\mathrm{1}}{M}}\sum _{i=\mathrm{1}}^M{\mathit{x}}_k^{i,f}.\end{array}$$

To compose the state deviation matrix, the value of ${\stackrel{\mathrm{‾}}{\mathit{x}}}_k^f$ is subtracted from the elements of the state vector as

$$\begin{array}{}\text{(9)}& {\mathbf{X}}_k^f=[{\mathit{x}}_k^{\mathrm{1},f}-{\stackrel{\mathrm{‾}}{\mathit{x}}}_k^f{\mathit{x}}_k^{\mathrm{2},f}-{\stackrel{\mathrm{‾}}{\mathit{x}}}_k^f{\mathit{x}}_k^{\mathrm{3},f}-{\stackrel{\mathrm{‾}}{\mathit{x}}}_k^f\mathrm{\cdots }{\mathit{x}}_k^{M,f}-{\mathit{x}}_k^f].\end{array}$$

The observation from the CMRSET for the k time step is the vector

$$\begin{array}{}\text{(10)}& {\mathit{y}}_k={\text{AET}}_k,\end{array}$$

which is a scalar value because of the choice of matching observation and assimilation frequencies. Because of the 8 d frequency of the observations, the average AET over 8 d simulated by the models is

$$\begin{array}{}\text{(11)}& {\widehat{\mathit{y}}}_k^{i,f}={\displaystyle \frac{\mathrm{1}}{\mathrm{8}}}\sum _{s=\mathrm{1}}^t{\text{AET}}_s^{i,f},\end{array}$$

with s being the individual UZM steps. The average over the ensemble population (M) of Eq. (11) reads

$$\begin{array}{}\text{(12)}& {\stackrel{\mathrm{‾}}{\mathit{y}}}_k^f={\displaystyle \frac{\mathrm{1}}{M}}\sum _{i=\mathrm{1}}^M{\widehat{\mathit{y}}}_k^{i,f}.\end{array}$$

The matrix for observation–simulation deviation is composed as

$$\begin{array}{}\text{(13)}& {\mathbf{Y}}_k^f=[{\widehat{\mathit{y}}}_k^{\mathrm{1},f}-{\stackrel{\mathrm{‾}}{\mathit{y}}}_k^f{\widehat{\mathit{y}}}_k^{\mathrm{2},f}-{\stackrel{\mathrm{‾}}{\mathit{y}}}_k^f{\widehat{\mathit{y}}}_k^{\mathrm{3},f}-{\stackrel{\mathrm{‾}}{\mathit{y}}}_k^f\mathrm{\cdots }{\widehat{\mathit{y}}}_k^{M,f}-{\stackrel{\mathrm{‾}}{\mathit{y}}}_k^f].\end{array}$$

Combining the matrices calculated above, it is possible to calculate the background state covariance matrix

$$\begin{array}{}\text{(14)}& {\mathbf{PH}}_k^T={\displaystyle \frac{\mathrm{1}}{M-\mathrm{1}}}{\mathbf{X}}_k^f{\mathbf{Y}}_k^{fT}\end{array}$$

and the observation–simulation error covariance matrix

$$\begin{array}{}\text{(15)}& {\mathbf{HPH}}_k^T={\displaystyle \frac{\mathrm{1}}{M-\mathrm{1}}}{\mathbf{Y}}_k^f{\mathbf{Y}}_k^{fT}.\end{array}$$

These lead to the formulation of the Kalman gain as

$$\begin{array}{}\text{(16)}& {\mathbf{K}}_k={\displaystyle \frac{{\mathbf{PH}}_k^T}{{\mathbf{HPH}}_k^T+{\mathbf{R}}_k}},\end{array}$$

where R_k is the observation error covariance matrix. The Kalman gain transfers the difference between the observed and simulated AET to the state variables with the updating equation

$$\begin{array}{}\text{(17)}& {\mathit{x}}_k^{i,a}={\mathit{x}}_k^{i,f}+{\mathbf{K}}_k[{\mathit{y}}_k-{\widehat{\mathit{y}}}_k^{i,f}+v_k^i],\end{array}$$

where $v_k^i$ is a random number with mean 0 and standard deviation as the observation error (i.e. 0.2 mm d⁻¹).

According to Gelsinari et al. (2020), the state variable update had to be constrained to preserve numerical stability. This was equally true for both models and applies to the WT levels and SM. A limitation of ±50 % of the prior values is applied for the SM content of Configuration-1 and, similarly, to the pressure head variable of Configuration-2. This avoids the convergence problem in physically based models reported in Zhang et al. (2018).

2.4.1 Ensemble generation

The generation of a statistically meaningful ensemble, which preserves the relationship between AET and WT levels obtained during the calibration, is crucial for the application of the EnKF (Gelsinari et al., 2020). A number of ensemble generation techniques were applied to the two configurations, and a consistent approach for both configurations was adopted. The average of the ratios between ensemble skill and ensemble spread, which should tend to 1 over the verification period, and between ensemble skill and mean square error, which should tend to $\sqrt{(M+\mathrm{1})/\mathrm{2}M}$ (Talagrand et al., 1997; De Lannoy et al., 2006), were calculated on the modelled AET values.

First, a simple perturbation of forcing inputs, by adding a random number sampled from Gaussian distributions with different standard deviations, as performed by Gelsinari et al. (2020), was tested. By perturbing the forcing inputs alone, the ensemble spread was not reaching appropriate values. Thus, a mixed method involving the perturbation of both inputs and parameters, with the latter perturbed by adding a random number proportionally to the calibrated value, was applied. For the UZMs, the parameters selected for the perturbation were K_s and root depth and for MODFLOW the saturated K_h and S_y. Initial conditions of WT levels were also perturbed to induce a good spread in the ensemble from the early stages of the simulation. The Talagrand et al. (1997) verification skills were applied to the ensembles generated with the aforementioned approach, and the most adequate ensembles for the two configurations were retained. The scores obtained for the two ratios were comparable to others found in the literature (e.g. De Lannoy et al., 2006; Pauwels and De Lannoy, 2009; Gelsinari et al., 2020). These ensembles are defined as the open loop, which represents the “prior” distribution. After applying the filter, the resulting distribution is called the assimilation run and represents the “posterior”.

2.5 Verification skills

In this section, the results for the open loop and assimilation runs are assessed. This is conducted by analysing the error between the prediction of the model and the observations. The common error metrics used to assess the overall errors in these models are the root mean square error (RMSE), the Pearson correlation coefficient (r), and the continuous ranked probability score (CRPS) (Hersbach, 2000).

The RMSE and r are defined as

$$\begin{array}{}\text{(18)}& \text{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{L}}\sum _{k=\mathrm{1}}^L(o_k-f_k{)}^{\mathrm{2}}},\end{array}$$

where o_k is the observations, f_k is the modelled variables at time step k, and L is the size of the data set. The RMSE is an important metric which measures the square of the difference in the errors and is presented to convey a possible broad overall error between the observations and the model. A disadvantage of RSME is the excessive weight of large outliers.

The next component for analysing the performance in verifying the results is the Pearson correlation coefficient to understand the relationship between the observed values and the predicted model values. The Pearson correlation coefficient (r) is defined as

$$\begin{array}{}\text{(19)}& r={\displaystyle \frac{{\sum }_{k=\mathrm{1}}^L(o_k-\stackrel{\mathrm{‾}}{o})(f_k-\stackrel{\mathrm{‾}}{f})}{\sqrt{{\sum }_{k=\mathrm{1}}^L(o_k-\stackrel{\mathrm{‾}}{o}{)}^{\mathrm{2}}\cdot {\sum }_{k=\mathrm{1}}^L(f_k-\stackrel{\mathrm{‾}}{f}{)}^{\mathrm{2}}}}}.\end{array}$$

In particular, this investigates the strength of the linear relationship between the predicted and observed values as they proceed through time. A value of r>0 implies a positive relationship; the closer the value of r is to 1, the stronger and more accurate the relationship.

The CRPS is a measure to quantify the difference between the predicted value and the observed cumulative distribution in terms of the probabilistic distributions for each time step. The CRPS is calculated, at a specific time step, from the cumulative distribution function given by the ensemble simulation of the variable of interest x (i.e. AET and WT levels) as

$$\begin{array}{}\text{(20)}& {\text{CRPS}}_k=\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}\left[P\right(x{)}_k-P_{\mathrm{0}}(x{)}_k{]}^{\mathrm{2}}\mathrm{d}x,\end{array}$$

where P₀ is the observation distribution at the time step (k), and P(x) is the cumulative distribution function. As the observation (x₀) is usually a single value, P₀ is formulated as $P_{\mathrm{0}}=H(x-x_{\mathrm{0}})$, H being the Heaviside function. The CRPS is applied to reinforce the value of the result as it is specifically designed to assess probabilistic simulations and is increasingly being used in hydrologic ensemble simulations. The reasons are that it intrinsically weighs errors by assigning a lower weight to the largest residuals (Schneider et al., 2020), thus accounting for observations that in other cases are defined as outliers. Therefore, it is the preferable measure in determining the error in forecasting models since it is more robust to outliers, producing a more representative result. Note that a value of the CRPS of zero is only possible in the case of a perfect deterministic forecast. Thus, the lower the value of the CRPS, the better the model performance.

This is calculated over the entire simulation period, and the average CRPS is defined as

$$\begin{array}{}\text{(21)}& \stackrel{\mathrm{‾}}{\text{CRPS}}={\displaystyle \frac{\mathrm{1}}{L}}\sum _{k=\mathrm{1}}^L{\text{CRPS}}_k,\end{array}$$

where L is the number of observations. This permits an analysis of the measures and a comparison of the RMSE and the CRPS. In this experiment, the models are naturally stochastic processes, allowing the CRPS to produce a more representative value and robust measure for the errors compared to the RMSE. In conclusion of this section, all three measures will be used to assess the performance of the filter.

3 Results and discussion

3.1 Deterministic runs

During the calibration with the PSO, the dynamics of the parameter optimisation algorithm was monitored, showing that the MODFLOW saturated hydraulic conductivity (K_h) had a consistent tendency towards high values (100 m d⁻¹ or higher) in order to minimise Eq. (4). This was interpreted as an effect of the AET component on the objective function, which was causing the UZMs to transpire water directly from the WT to compensate for the low AET values. The boundary conditions for the groundwater model were thus modified by imposing a constant head boundary with shallower WT depth, which maintained K_h at a plausible order of magnitude (Table 2).

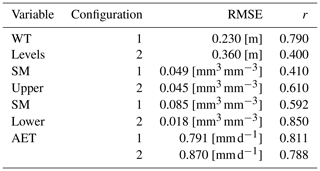
With the calibration technique proposed in Sect. 2.3, the coupled models were able to simultaneously reproduce the dynamics of both the WT and ET for the two configurations. Configuration-1 performs better overall in the representation of the WT dynamics with a RMSE of 0.23 m, while the RMSE of Configuration-2 is slightly larger, being 0.36 m. Configuration-1 also shows a higher correlation coefficient (0.790 vs. 0.400) for the WT. Configuration-1 shows a lower temporal variability than Configuration-2, but the latter better matches the temporal evolution of the WT. There is a time lag between groundwater observations and model WT fluctuation for Configuration-2, which also explains the higher RMSE and lower correlation. This lag may be induced by preferential flow that the Richards equation does not account for or by a slower response of the WT to the meteorological input that is discussed later in this section.

Figure 4 Observed and modelled (a) WT fluctuations and (b) AET after calibration.

Table 2 Results for the calibrated runs.

The soil heterogeneity is represented differently by the two configurations. Configuration-2, which is physically based, can represent the heterogeneity of the soil column, as shown in Fig. 5d, where a sharp variation of the SM content at 1.7 m depth is caused by the different soil parameters. Configuration-1 has no ability to explicitly account for duplex soil; thus the soil profile does not show sharp variations of the water content. However, it can account for the decay of the hydraulic conductivity along the soil column. Because of these reasons, the modelled SM from Configuration-2 shows a good agreement with the observations, especially in the lower soil (Fig. 5f). Configuration-1 has a low SM RMSE (0.049 mm³ mm⁻³) and a Pearson correlation coefficient r of 0.41 for the upper soil (b), but the resulting SM is consistently below the observed values in the bottom soil (panel c), with an RMSE of 0.137 mm³ mm⁻³. Both configurations report a higher correlation for the lower soil.

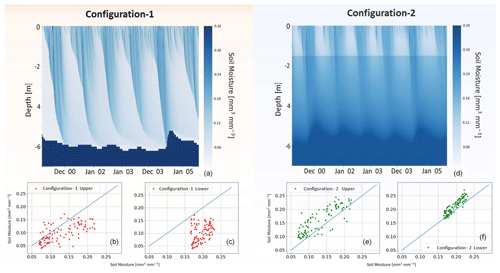
Figure 5 Temporal evolution of the SM contents and WT levels. Panels (a, d) show the entire modelled column, including the fluctuation of the WT (i.e. the dark blue area). Panels (b, e) represent the modelled and observed water content for the upper soil (averaged over 0–300 mm depth). Panels (c, f) show these results for the lower soil (averaged over the interval 1500–1800 mm depth).

For AET, Configuration-1 yields good results with a lower RMSE and similar correlation when compared to Configuration-2. In particular, Configuration-2, being physically based, underestimates the simulated AET for the Southern Hemisphere late summer and early autumn, as shown in Fig. 4b. In this period, the soil water content is low (Fig. 5d), and the roots take up water directly from groundwater. This can be interpreted as an effect of the coupling to the groundwater model. Configuration-1, which is conceptually based, with a rooting depth of 8.0 m, is able to extract water directly from the water table and immediately transforms it into AET. Configuration-2, with a rooting depth of 2.9 m, achieves this by reducing the pressure head along the soil column. Thus water has to flow across a part of the unsaturated zone before becoming available for direct plant transpiration, reducing the rapid response of the model to the forcing inputs. This also explains the lag in the WT dynamics previously described. Another possible reason for the underestimation of AET is the two oxygen stress parameters that reduce transpiration in conditions close to saturation (Table 1). These parameters are calibrated and kept constant during the simulation period. Configuration-2 has shown to be highly sensitive to these parameters, while Configuration-1 does not include this process.

3.2 Ensemble simulations

The generation of the ensemble was found to be a key step of the method. The simple perturbation of forcing inputs was not able to generate a sufficiently broad ensemble spread, particularly for Configuration-2. For both configurations, the combined perturbation of parameters and forcing inputs induced more accurate ensembles, in accordance with the ensemble validation skills calculated on the first year of the data set, excluding the 10 first time steps to avoid the influence of the initial conditions; the validation is thus applied from the 10th to the 45th time step. For the meteorological data, the best ensembles are obtained by perturbing the input with a random number sampled from a Gaussian distribution having a standard deviation proportional to the value of the forcing inputs (i.e. 50 % for Configuration-1 and 10 % for Configuration-2). For parameters, the last column of Table 1 lists the coefficient of variation. Additionally, for Configuration-2, S_y has a lower limit of 0.1 to preserve numerical stability of the coupled models.

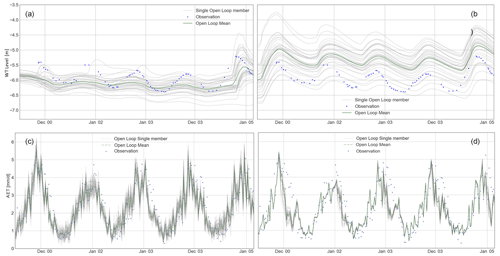
Figure 6 WT levels and AET and spread of the open-loop ensembles for Configuration-1 (a, c) and Configuration-2 (b, d).

In the case of Configuration-1, which is conceptually based, the WT level spread of the open-loop ensemble is consistently covering the observations (Fig. 6a). The mean of the ensemble is close to the observations but does not follow the seasonal variability appropriately. The associated spread of the AET for Configuration-1 is wider than that of Configuration-2. More specifically, the latter is narrow during wet periods (i.e. April to November) and becomes wider for the dry period (Fig. 6c and d). A similar effect, with a larger magnitude, was reported during the ensemble generation phase and led to the perturbation of both the meteorological inputs and the parameters, as explained in Sect. 2.4.1.

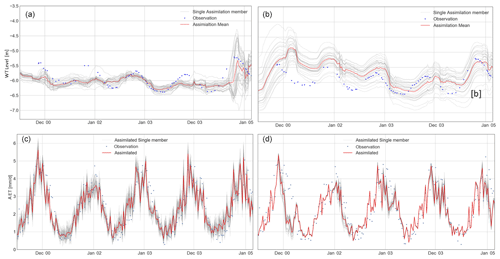
Figure 7 WT levels and AET and spread of the assimilation run for Configuration-1 (a, c) and Configuration-2 (b, d).

The spread of the WT levels for Configuration-2 (see Fig. 6b) covers the WT observations for most of the simulations and is wider than for Configuration-1. The mean represents the amplitude of the seasonal fluctuations better as compared to Configuration-1 but leads to a shallower WT as a result of the perturbation of the forcing inputs.

Table 3 RMSE, correlation and $\stackrel{\mathrm{‾}}{\text{CRPS}}$ for three variables between the open loop and the assimilation.

Table 3 summarises the RMSE, r, and $\stackrel{\mathrm{‾}}{\text{CRPS}}$ values for AET, WT levels, and SM contents (upper and lower soil layers) and compares the results of the assimilation run to the open loop. The table allows for a quick comparison between the results given by the RMSE, standardly used and understood across the modelling community, and the CRPS averaged over the simulation period (i.e. $\stackrel{\mathrm{‾}}{\text{CRPS}}$), which allows for an appropriate and representative analysis of the ensemble distributions. For both configurations, the AET assimilation slightly decreases the RMSE and the $\stackrel{\mathrm{‾}}{\text{CRPS}}$ and improves the correlations. In particular, the RMSE of AET for Configuration-1 reduces from 0.76 mm d⁻¹ for the open loop to 0.73 mm d⁻¹. The RMSE of AET for Configuration-2 reduces from 0.83 mm d⁻¹ for the open loop to 0.81 mm d⁻¹. A similar pattern is observed for the $\stackrel{\mathrm{‾}}{\text{CRPS}}$, with the relative percentage change improvements varying from 4.3 % to 6.1 %. In this case, the $\stackrel{\mathrm{‾}}{\text{CRPS}}$ reinforces the relevance of the RMSE results. The correlation also improves, although marginally, for both configurations (i.e. +0.01). However, these are non-trivial results as the data assimilation, through the EnKF, is designed to only improve the model states. Therefore, the observed reduction in AET errors suggests that the model states (i.e. WT, SM) updated by the filter are contributing to better modelling of other hydrological quantities (e.g. AET).

In particular there are instances in Configuration-2 where the assimilation is not able to improve AET in the first quarter of 2001 and, to a lesser extent, at the beginning of 2003. This causes poorer WT simulations' performances during these periods, as seen in Fig. 7b and highlighted by the higher values in Fig. 8b. Here, the filter is trying to increase the amount of water in the system to match the higher assimilated observation, which is a correct application of the methodology. Thus, the WT is made shallower by the filter, but this is not reflected in a higher modelled AET. The reason for this is the behaviour of the SWAP vegetation parameter oxygen stress. The filter is increasing the pressure head of the system, in an attempt to provide more water to transpire, but the actual transpiration from the plant is hindered by SWAP, which recognises the soil to be too saturated for the plant to transpire. The EnKF then causes the WT to rise and increases the amount of recharge entering the groundwater. When the observed AET is lower than the simulations, the filter reduces the pressure head, and the model allows the plant to transpire. Therefore, in the two time steps after this effect, the modelled AET is higher than the observation, after which this phenomenon disappears. This artefact is not seen in Configuration-1 as the oxygen stress is not accounted for.

Figure 8 CRPS WT levels and AET for Configuration-1 (a, c) and Configuration-2 (b, d).

In Fig. 8, the single bars represent the CRPS_k computed for each time the observations (WT levels above, AET below) are available over the entire simulation period. For this reason, the length of these data sets is different, as the CMRSET observations' temporal interval is 8 d, while the WT levels' observations are more infrequent and present gaps. Generally, lower CRPS values are seen in Configuration-1 for both WT levels and AET. CRPS values for the WT level are substantially reduced in the first part of the simulation for both configurations, with Configuration-1 performing particularly well between August 2002 through July 2003 and in reducing the prior errors around the end of 2004. Analysing the CRPS values for AET (see Fig. 8c), in most cases the assimilation improves the CRPS values, with the exemption of the middle of 2004. This is also seen in Fig. 7 when the assimilation fails to reduce the AET in the winter of 2004. For Configuration-2, the WT level CRPS starts with higher values, and apart from the spikes of 2001 (discussed earlier), it presents continuous, constant improvements, outperforming Configuration-1 in the last part of the simulation. This pattern is similarly observed for the CRPS calculated for AET.

For both configurations, the assimilation improves the RMSE and $\stackrel{\mathrm{‾}}{\text{CRPS}}$ when compared to the open loop runs. The best results are obtained for Configuration-1, showing a RMSE of 0.236 m with a 15 % error reduction compared to the open loop; this result is confirmed by the $\stackrel{\mathrm{‾}}{\text{CRPS}}$ of 0.134 (error reduction of 16 %). Configuration-2 resulted in a substantial RMSE reduction of 38.9 % as compared to the open loop. The magnitude of these improvements is corroborated by the $\stackrel{\mathrm{‾}}{\text{CRPS}}$, with a value after the assimilation of 0.229 from the prior of 0.426, which translates to an improvement of around 46 %. However, RMSE and $\stackrel{\mathrm{‾}}{\text{CRPS}}$ values (0.307 and 0.229 m, respectively) are still higher in Configuration-1 than in Configuration-2. Apart from the oxygen stress artefacts explained above, the assimilation run of Configuration-2 is consistently better than the open loop. This is not always the case for Configuration-1, where the open loop was already performing well. The correlation remains largely unchanged for Configuration-1 and reduces for Configuration-2, mainly due to the updates during the first quarter of 2001 and beginning of 2003.

For SM, the results are reported in Table 3, divided into the upper and lower soil. The open loop of Configuration-1 presents a RMSE of 0.045 mm³ mm⁻³ for the upper soil and 0.102 mm³ mm⁻³ for the lower soil. In the latter, the simulated water contents are consistently lower than the observations. This is mainly due to the model's inability to represent capillary rise. The assimilation only marginally improved the SM content, with slightly better results for the bottom part of the soil, where the RMSE was reduced to 0.098 mm³ mm⁻³. The open loop of Configuration-2 has a lower RMSE, 0.041 and 0.017 mm³ mm⁻³ for the top and bottom part of the soil, respectively. However, it slightly overestimates the SM content for the entire column. This is consistent with the shallower WT (i.e. more water in the system) observed for the WT levels in the open loop (Fig. 6d). The assimilation did not improve the top layer SM content, with an RMSE of 0.042 mm³ mm⁻³. However, effects of the assimilation are seen for the SM content of the lower soil, for which the best results are obtained (i.e. 0.015). For SM, the $\stackrel{\mathrm{‾}}{\text{CRPS}}$ is unable to show significant variations and does not add valuable information. Although the improvements for SM are limited and cannot be considered conclusive, the feasibility for this framework of updating the entire soil column is a positive result of the assimilation of AET rates, as opposed to the assimilation of remotely sensed SM values. The latter usually results in stronger updates in the upper parts of the soil because of the reduced correlation between the SM contents in the upper and deeper parts of the soil column (Pipunic et al., 2014).

Generally, these results consolidate the synthetic approach in Gelsinari et al. (2020) and further confirm that the assimilation framework is not only able to update and improve the WT level, which is a prognostic variable of the coupled models, but also the modelled AET and consequently the recharge to the WT. In addition, albeit marginally, the filter improves the unsaturated zone state variables regardless of the manner in which the SM content is calculated (volumetric SM or pressure head).

4 Conclusions

This study validates the assimilation of the satellite-based actual evapotranspiration (AET) data set (CMRSET) into two unsaturated zone models (UZM) coupled to MODFLOW. The two UZMs form two configurations, one using a conceptual water balance model (UnSAT) and the other using a physically based agro-hydrological model (SWAP). These configurations are applied to a semi-arid pine plantation in the south-east of South Australia, where the WT is within reach of the trees' root system.

The most important findings can be summarised as follows:

• Calibration. This study shows the need to calibrate the model using a multi-objective function, with normalised components of water table (WT) and AET. In this way, both configurations represent the WT-AET dynamics and are thus able to benefit from the assimilation of AET observations.

• Configuration-1. The assimilation of AET values through the ensemble Kalman filter (EnKF) using a conceptual UZM produced the best results for the prognostic variable WT levels and the diagnostic fluxes of AET. SM values were updated in both the upper and lower parts of the soil column, although only to a minor extent. In addition, because of the model conceptualisation, the mismatch in the lower part of the soil is considerably larger than for Configuration-2. The reduced number of parameters of this configuration allows for a simpler calibration, which is able to represent the WT dynamics. Similarly, the generation of an appropriate ensemble is more straightforward, mostly due to the model conceptualisation, which allows the WT to respond quickly to direct root water extraction by transpiration.

• Configuration-2. The AET assimilation into a physically based UZM, based on the Richards equation, produced the largest improvements to the WT levels, with a better representation of the soil heterogeneity. Improvements to AET fluxes were similar for Configuration-1. For SM, the impact of the assimilation algorithm was small, with a positive update for the lower soil layers and a negative update for the upper layers. Here, the calibration involved a larger number of parameters and produced a good representation of the SM dynamics. However, due to the non-linearity introduced with the coupling, errors in the WT levels and AET fluxes are higher. In addition, the ensemble generation is constrained by the high model parameterisation, making it more difficult to produce an appropriate ensemble that preserves the AET–WT relationship.

• AET information. The updating of the entire soil column is an advantage of the assimilation of remotely sensed AET over satellite SM retrievals. AET rates express the moisture status of the entire root zone. Thus, assimilating AET has the potential to overcome the SM assimilation tendency to produce stronger updates in the most superficial part of the soil because of the reduced correlation between the upper and lower SM contents. This experiment only showed the feasibility of the proposed assimilation framework to improve SM contents. Preliminary results indicated that Configuration-2 is preferred to conduct more experiments in order to quantify the significance of the SM updates.

In conclusion, the numerical experiment explored the added value of AET information for constraining unobservable estimates (i.e. net recharge) calculated by hydrogeological models. Improving the AET fluxes led to better recharge estimates. Thus, as recharge is a key quantity driving the WT dynamics, the link between AET and WT in the model is strengthened. It was shown that it is possible to use either a conceptual or a physically based UZM in the assimilation of satellite-based AET estimates to inform hydrogeological models. The assimilation results have been quantified using standard metrics, such as RMSE and r, and reinforced by calculating the CRPS, which is a specifically designed metric for ensemble simulations. The CRPS is applied as it is a measure to determine a more representative error, since it is more robust in accounting for uncertainty in stochastic models. The findings indicate that a simple conceptual model may be sufficient for this purpose; thus using one configuration over the other should be motivated by the specific purpose of the simulation and the information available.

This study contributes to unlocking the potential of using AET observations to inform hydrological models, with the aim of reducing the uncertainty in the outputs, and it represents a step towards the use of satellite-based AET retrievals for water resources management. For future applications at larger scales, more research is to be conducted in areas with different groundwater, vegetation, and soil conditions, with the intent of prioritising regions where the AET assimilation is more effective.