Disentangling temporal and population variability in plant root water uptake from stable isotopic analysis: when rooting depth matters in labeling studies

Isotopic labeling techniques have the potential to minimize the uncertainty of plant root water uptake (RWU) profiles estimated using multisource (statistical) modeling by artificially enhancing the soil water isotopic gradient. On the other end of the modeling continuum, physical models can account for hydrodynamic constraints to RWU if simultaneous soil and plant water status data are available.

In this study, a population of tall fescue (Festuca arundinacea cv. Soni) was grown in amacro-rhizotron and monitored for a 34 h long period following the oxygen stable isotopic (¹⁸O) labeling of deep soil water. Aboveground variables included tiller and leaf water oxygen isotopic compositions (δ_tiller and δ_leaf, respectively) as well as leaf water potential (ψ_leaf), relative humidity, and transpiration rate. Belowground profiles of root length density (RLD), soil water content, and isotopic composition were also sampled. While there were strong correlations between hydraulic variables as well as between isotopic variables, the experimental results underlined the partial disconnect between the temporal dynamics of hydraulic and isotopic variables.

In order to dissect the problem, we reproduced both types of observations with a one-dimensional physical model of water flow in the soil–plant domain for 60 different realistic RLD profiles. While simulated ψ_leaf followed clear temporal variations with small differences across plants, as if they were “onboard the same roller coaster”, simulated δ_tiller values within the plant population were rather heterogeneous (“swarm-like”) with relatively little temporal variation and a strong sensitivity to rooting depth. Thus, the physical model explained the discrepancy between isotopic and hydraulic observations: the variability captured by δ_tiller reflected the spatial heterogeneity in the rooting depth in the soil region influenced by the labeling and may not correlate with the temporal dynamics of ψ_leaf. In other words, ψ_leaf varied in time with transpiration rate, while δ_tiller varied across plants with rooting depth.

For comparison purposes, a Bayesian statistical model was also used to simulate RWU. While it predicted relatively similar cumulative RWU profiles, the physical model could differentiate the spatial from the temporal dynamics of the isotopic composition. An important difference between the two types of RWU models was the ability of the physical model to simulate the occurrence of hydraulic lift in order to explain concomitant increases in the soil water content and the isotopic composition observed overnight above the soil labeling region.

1 Introduction

Since the seminal work of Washburn and Smith (1934) where it was first reported that willow trees did not fractionate hydrogen stable isotopes in a hydroponic water solution during root water uptake (RWU), water stable isotopologues (¹H²H¹⁶O and ${}^{\mathrm{1}}{\mathrm{H}}_{\mathrm{2}}^{\mathrm{18}}\mathrm{O}$) have been used as indicators for plant water sources in soils. In their review, Rothfuss and Javaux (2017) reported on no less than 40 publications between 2015 and 2016 in which RWU was retrieved from stable isotopic measurements. Novel measuring techniques (e.g., cavity ring-down spectroscopy, CRDS, and off-axis integrated cavity output spectroscopy, ICOS) that provide methods for fast and cost-effective water stable isotopic analyses certainly enable and emulate current research in that field. Water stable isotopologues are no longer powerful tracers waiting for technological developments (Yakir and Sternberg, 2000) but are on the verge of being used to their full potential to address eco-hydrological research questions and identify processes in the soil–plant–atmosphere continuum (Werner et al., 2012; Dubbert and Werner, 2019; Sprenger et al., 2016).

The isotopic determination of RWU profiles is based on the principle that the isotopic composition of xylem water at the outlet of the root system (i.e., in the first aerial and non-transpiring node of the plant) equals the sum of the product between the soil water isotopic composition and the relative contribution to RWU across plant water sources. Results only show reasonable precision when (i) the soil water isotopic composition depth gradient is strong and monotonic (which avoids issues of identifiability) and (ii) the temporal dynamics of RWU and the soil water isotopic composition are relatively low. Condition (i) is mostly fulfilled at the surface of the soil, whereas the soil water isotopic composition gradients usually become lower or nonexistent with increasing depth (due to the isotopic influence of the groundwater table and increasing dispersion with depth). As illustrated by Oerter and Bowen (2019), the lateral variability of the soil water isotopic composition profiles can become significant in the field and could have great implications for the representability and meaningfulness of isotopic-derived estimates of RWU profiles. Condition (ii) is often neglected, but it is required due to the instantaneous nature of the sap flow samples.

To overcome these limitations, labeling pulses have been increasingly used in recent works to artificially alter the natural isotopic gradients (e.g., Beyer et al., 2016, 2018; Grossiord et al., 2014; Jesch et al., 2018; Volkmann et al., 2016b). However, precise characterization of the artificial spatial (i.e., lateral and vertical) and temporal distributions of the soil water isotopic composition (driven by factors such as soil isotopic water flow) is crucial. The punctual assessments of the isotopic composition profiles following destructive sampling in the field and the subsequent extraction of water in the laboratory might not be spatially or temporally representative and can lead to erroneous estimates of RWU profiles (Orlowski et al., 2018, 2016).

The vast majority of isotopic studies use statistical (e.g., Bayesian) modeling to retrieve the RWU profile solely from the isotopic composition of water extracted in the soil and the shoot (Rothfuss and Javaux, 2017). However, when data on soil and plant water status are available, hydraulic modeling tools can also be used to connect different data types in a process-based manner and estimate root water uptake profiles (Passot et al., 2019). Some of the most simplistic models use one-dimensional relative root distribution and plant-scale hydraulic parameters (Sulis et al., 2019), whereas the most complex models rely on root architectures and root segment permeabilities (Meunier et al., 2017c). Only a handful of studies have coupled isotopic measurements in plant tissues and soil material with models describing RWU in a mechanistic manner. For instance, Meunier et al. (2017a) could both locate and quantify the volume of redistributed water by Lolium multiflorum by labeling of the soil with ¹⁸O-enriched water under controlled conditions.

Building on the work of Meunier et al. (2017a), the objectives of the present study were (i) to model the temporal dynamics of the isotopic composition of the RWU of a population of Festuca arundinacea cv. Soni (tall fescue) in a physically based manner (i.e., by accounting for soil, plant, and environmental factors) during a semi-controlled experiment following the isotopic labeling of deep soil water, (ii) to investigate the implication of the model-to-data fit quality in terms of the meaningfulness of the isotopic information to reconstruct RWU profiles, and (iii)  to confront the simulated root water uptake profiles with estimations obtained on the basis of isotopic information alone (i.e., provided by a Bayesian mixing model).

2 Material and methods

Our experiment consisted of supplying labeled water to a macro-rhizotron in which tall fescue was grown. Data on the soil and plant oxygen stable isotopic composition and hydraulic status were monitored for 34 h. In the following, the oxygen isotopic composition of water will be expressed in per mil (‰) on the “delta” (δ¹⁸O) scale with respect to the international water standard V-SMOW (Vienna Standard Mean Ocean Water; Gonfiantini, 1978).

2.1 Rhizotron experimental setup

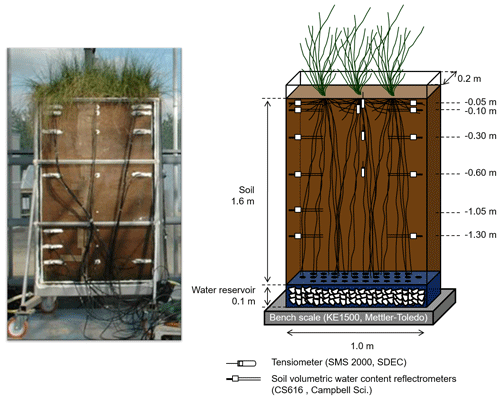
The macro-rhizotron (which had the following dimensions: 1.6 m ×1.0 m ×0.2 m; see picture in Appendix A) was placed inside a glasshouse (INRA, Lusignan, France), where it was continuously weighed (KE1500, Mettler-Toledo, resolution of 20 g) to monitor water effluxes (i.e., bare soil evaporation or evapotranspiration). Underneath the soil compartment and in contact with it, a water reservoir (height of 0.1 m) that was filled with gravel acted as the water table and allowed the supply of water to the rhizotron. The rhizotron was equipped with two sets of CS616 time domain reflectometer (TDR) profiles (Campbell Scientific, USA) with 30 cm long probe rods positioned at six depths (−0.05, −0.10, −0.30, −0.60, −1.05, and −1.30 m) and one profile of tensiometers (SMS 2000, SDEC-France) located at four depths (−0.05, −0.10, −0.30, and −0.60 m) in order to monitor the evolution of the soil water volumetric content (θ, in m³ m⁻³) and matric potential (ψ_soil, in MPa). Finally, relative humidity (RH, %) was recorded above the vegetation with one humidity and temperature probe (HMP45D, Vaisala, Finland). The transparent polycarbonate sides (front and back) allowed for daily observations of the root maximal depth. The experimental setup allowed for the precise control of the amount and δ¹⁸O composition of soil input water. Another important feature was the soil depth (i.e., 1.60 m), which minimized the influence of the water table on superficial layers' water content and δ¹⁸O.

2.2 Soil properties and installation

The soil substrate originates from an agricultural field that is part of the Observatory of Environment Research (ORE), INRA, Lusignan, France (0^∘60 W, 46^∘250 N) which is classified as Dystric Cambisol (with a particle size distribution of 15 % sand, 65 % silt, and 20% clay). Prior to installation in the rhizotron, the substrate was sieved at 2 mm and dried in an air oven at 110 ^∘C for 48 h to remove most of the residual water. A total of 450 kg of soil was filled into the rhizotron in 0.10 m increments and compacted in order to reach a dry bulk density value of ρ_b=1420 kg m⁻³. The closed-form soil water retention curve of van Genuchten (1980) was derived in a previous study by Meunier et al. (2017a) from synchronous measurements of soil water content and matric potential from the saturated to the residual water content (see Appendix B for its hydraulic parameters). It was used to compute the soil water matric potential (ψ_soil, in MPa) on the basis of volumetric water content data during the present experiment.

2.3 Experimental protocol

After installation, the soil was gradually flooded with local water (${\mathit{\delta }}^{\mathrm{18}}\mathrm{O}=-\mathrm{6.8}$ ‰) from the bottom reservoir up to the top of the profile for a period of 3 d in order to reduce the initial lateral and vertical heterogeneities in water content and δ¹⁸O as much as possible. The tall fescue (Festuca arundinacea cv. Soni) was sown at a seeding density of 3.6 g m⁻² (which, for the rhizotron surface area of 0.2 m², corresponded to roughly 300 plants) when the soil water content reached 0.25 m³ m⁻³ (corresponding to pF 2.3) at −0.05 m, as measured by the soil water sensors, and emerged 12 d later. During a period of 165 d following seeding, the tall fescue cover was exclusively watered from the reservoir with local water in order to (i) keep the soil bottom layer (< −1.3 m) close to water saturation and (ii) not disrupt the natural soil water δ¹⁸O profile.

A total of 166 d after seeding (DaS 166) the following conditions were fulfilled: (i) there was a strong soil water content gradient between the soil deep [−1.5 m, −1.0 m] and superficial [−0.3 m, 0 m] layers, and (ii) the tall fescue roots had reached a depth of −1.5 m (observed through the polycarbonate transparent sides). That same day at 17:00 LT, the reservoir's water was labeled and its δ¹⁸O was measured at +470 ‰. Soil was sampled before (DaS 166 at 15:45 LT) and after labeling on DaS 167 at 07:00 LT, DaS 167 at 17:00 LT, and DaS 168 at 05:00 LT, using a 2 cm diameter auger through the transparent polycarbonate side of the rhizotron on four occasions from the surface down to −1.3 m, for the determination of the soil gravimetric water content (θ_grav, in kg kg⁻¹) and the oxygen stable isotopic composition (δ_soil, in ‰). The gravimetric water content was then converted to the volumetric water content ($\mathit{\theta }={\mathit{\theta }}_{\mathrm{grav}}\times {\mathit{\rho }}_{\mathrm{b}}/{\mathit{\rho }}_{\mathrm{w}}$, in m³ m⁻³, where ρ_b is the bulk soil density and ρ_w is the water density). The hypothesis of a constant value for ρ_b across the reconstructed soil profile was further validated from the quality of the linear fit (a coefficient of determination, R², of 1.0) between the θ values measured by the sensors at the six available depths (−0.05, −0.10, −0.30, −0.60, −1.05, and −1.30 m) and those computed from θ_grav.

On 40 occasions during a 34 h long period, three whole plants were sampled from the vegetation (i.e., 120 plants were sampled in total from the cover). Each plant's tiller and leaves were pooled into two separate vials. Dead material as well as the oldest living leaf around each tiller were removed so as not to contaminate tiller samples with transpiring material (Durand et al., 2007). In addition, air water vapor was collected from the ambient atmosphere surrounding the rhizotron. The air was run at a flow rate of 1.5 L min⁻¹ through two glass cold traps in series immersed in a mixture of dry ice and pure ethanol at −80 ^∘C. Water from the plant (i.e., tillers and leaves) and soil samples was extracted by vacuum distillation for 14 to 16 h depending on the sample mass (e.g., ranging from 18 to 28 g for soil) at temperatures of 60 and 90 ^∘C, respectively. The residual water vapor pressure at the end of each successful extraction procedure invariably reached 10⁻¹ mbar. The oxygen isotopic compositions of tiller, leaf, and soil water (i.e., δ_tiller, δ_leaf, and δ_soil) and that of atmospheric water vapor (δ_atm) were measured with an isotope-ratio mass spectrometer (ISOPREP-18, Optima, Fison, Great-Britain, precision accuracy of 0.15 ‰). Finally, the leaf water potential (ψ_leaf, in MPa) was monitored with a pressure chamber on two leaves per sampled plant, and the evapotranspiration rate (in m d⁻¹) was derived from the changes in the mass of the rhizotron at the same temporal scale as plant sampling.

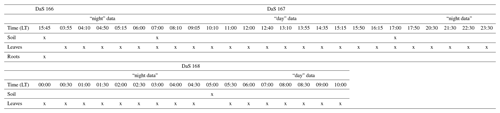
Root biomass was determined from the horizontal sampling of soil between the polycarbonate sides using a 2 cm diameter auger at soil depths of −0.02, −0.08, −0.10, −0.40, −0.55, −0.70, −0.90, −1.10, and −1.30 m. Each depth was sampled one to three times. Each soil core was washed of soil particles, and the roots were collected over a 0.2 mm mesh filter and dried at 60 ^∘C for 48 h. Finally, the root length density (RLD, in meters of root per cubic meter of soil, m m⁻³) distribution was determined from the root dry mass using the specific root length of 95 m g⁻¹ determined by Gonzalez-Dugo et al. (2005), which is explicitly for tall fescue. The reader is referred to Appendix C for an overview of the type and timing of the different destructive measurements during the intensive sampling period.

2.4 Modeling of RWU and δ_tiller

The experimental setup included about 300 tall fescue plants. In order to limit the computational requirement in the inverse modeling loop, we only generated 60 virtual root systems whose rooting depths ranged from a depth of −1.30 to −1.60 m (based on our own observations and those in the literature, e.g., Schulze et al., 1996; Fan et al., 2016) with the root architecture simulator CRootBox (Schnepf et al., 2018), so that the simulated RLD matched observations (Fig. 1a). In order to reach a total number of virtual plants representative of the number of plants in the experimental setup, each root system was replicated five times, forming a “group”. Each group was assumed to occupy 1/60 of the total horizontal area and was considered to be a “big root” hydraulic network (five identical plants per “big root”) with equivalent radial and axial hydraulic conductances (which neglects architectural aspects but accounts for each group's respective root length density profile).

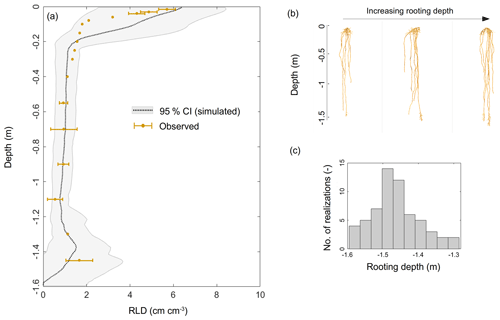
Figure 1 (a) Simulated (gray shading) and observed (brown dots) root length density profiles. Panels (b) and (c) illustrate the variability in the modeled root system architectures and rooting depths, respectively.

The radial soil–root conductance between the bulk soil and each group's (i) root surfaces in soil layer j (K_radial,j, m³ MPa⁻¹ d⁻¹), as derived by Meunier et al. (2017a), was assumed to be variable in time (t):

$$\begin{array}{}\text{(1)}& K_{\mathrm{radial},i,j}\left(t\right)={\displaystyle \frac{\mathrm{2}\mathit{\pi }{r}_{\mathrm{root}}\cdot l_{\mathrm{root},i,j}\cdot B_j\cdot L_{\mathrm{pr}}\cdot k_{\mathrm{soil},j}\left(t\right)}{B_j\cdot k_{\mathrm{soil},j}\left(t\right)+r_{\mathrm{root}}\cdot L_{\mathrm{pr}}}}\end{array}$$

Here, r_root (m) is the root radius, $l_{\mathrm{root},i,j}$ (m) is the root length of plants of group i in soil layer j, L_pr (m MPa⁻¹ d⁻¹) is the root radial hydraulic conductivity, k_soil,j (m² MPa⁻¹ d⁻¹) is the soil hydraulic conductivity in layer j, and B_j (dimensionless) is a geometrical factor simplifying the horizontal dimensions into radial domains between the bulk soil and root surfaces, as given by Schroeder et al. (2009):

$$\begin{array}{}\text{(2)}& B_j={\displaystyle \frac{\mathrm{2}(\mathrm{1}-{\mathit{\rho }}_j)(\mathrm{1}+{\mathit{\rho }}_j)}{\mathrm{2}{\mathit{\rho }}_j^{\mathrm{2}}ln{\mathit{\rho }}_j-{\mathit{\rho }}_j^{\mathrm{2}}+\mathrm{1}}},\end{array}$$

where ρ (dimensionless) represents the ratio of the distance between roots and the root averaged diameter. It can be deduced from the observed root length density (RLD_j, m m⁻³) as follows:

$$\begin{array}{}\text{(3)}& {\mathit{\rho }}_j={\displaystyle \frac{\sqrt{\frac{\mathrm{1}}{\mathit{\pi }{\mathrm{RLD}}_j}}}{r_{\mathrm{root}}}}\end{array}$$

The following soil hydraulic conductivity function of Mualem (1976) and van Genuchten (1980) was used:

$$\begin{array}{}\text{(4)}& k_{\mathrm{soil},j}\left(t\right)=k_{\mathrm{sat}}\cdot S_{e,j}^{\mathit{\lambda }}\left(t\right)(\mathrm{1}-(\mathrm{1}-S_{e,j}^{\mathrm{1}/m}{)}^m{)}^{\mathrm{2}},\end{array}$$

where k_sat (m² MPa⁻¹ d⁻¹), m (dimensionless), and λ (dimensionless) are soil hydraulic parameters (with $m=\mathrm{1}-\mathrm{2}/n$), and S_e,j, the relative water content (dimensionless), is computed from the saturated (θ_sat, m³ m⁻³) and residual (θ_res, m³ m⁻³) water contents as

$$\begin{array}{}\text{(5)}& S_{e,j}={\displaystyle \frac{{\mathit{\theta }}_j-{\mathit{\theta }}_{\mathrm{res}}}{{\mathit{\theta }}_{\mathrm{sat}}-{\mathit{\theta }}_{\mathrm{res}}}}\end{array}$$

Unlike the geometrical parameter B, which defines a domain geometry between the bulk soil and roots of the overall population, the l_root term is group specific (i) and uses the simulated root length density profiles over an area corresponding to 1/60 of the total setup horizontal area:

$$\begin{array}{}\text{(6)}& l_{\mathrm{root},i,j}={\displaystyle \frac{\mathrm{\Delta }{Z}_j\cdot A_{\mathrm{soil}}\cdot {\mathrm{RLD}}_{i,j}}{\mathrm{60}}},\end{array}$$

where ΔZ (m) and A_soil (m²) are the soil layer thickness and horizontal surface area, respectively.

To finalize the connection between root xylem and shoot, axial conductances per root system group (K_axial, m³ MPa⁻¹ d⁻¹) were calculated as equivalent “big root” specific axial conductance per root system group (k_axial, m⁴ MPa⁻¹ d⁻¹, to be optimized by inverse modeling) as follows:

$$\begin{array}{}\text{(7)}& K_{\mathrm{axial},j}={\displaystyle \frac{k_{\mathrm{axial}}}{\mathrm{\Delta }{Z}_j}}\end{array}$$

At each time step, both the total soil–root system conductance (K_soil–root, m³ MPa⁻¹ d⁻¹) and the standard sink distribution (SSF, dimensionless, summing to 1), were calculated from K_radial and K_axial, using the algorithm of Meunier et al. (2017b). The variable SSF is the relative distribution of water uptake in each soil layer under vertically homogeneous soil water potential conditions (Couvreur et al., 2012), and K_soil–root represents the water flow per unit water potential difference between the SSF-averaged bulk soil water potential and the “big leaf” (assuming a negligible stem hydraulic resistance; Steudle and Peterson, 1998).

Adding soil hydraulic conductance to the one-dimensional hydraulic model of Couvreur et al. (2014) yields the following solutions for the leaf water potential (ψ_leaf, MPa) and water sink terms (S, d⁻¹) whose formulation approaches that of Nimah and Hanks (1973):

$$\begin{array}{}\text{(8)}& {\mathit{\psi }}_{\mathrm{leaf}}\left(t\right)=-{\displaystyle \frac{T\left(t\right)}{K_{\text{soil–root}}\left(t\right)}}+\sum {\mathrm{SSF}}_j\left(t\right)\cdot {\mathit{\psi }}_{\mathrm{soil},j}\left(t\right),\end{array}$$

where 1/60 of the overall transpiration rate (T, m d⁻¹) is allocated to each group, and ψ_soil,j (Mpa) is the soil water potential in soil layer j.

$$\begin{array}{}\text{(9)}& S_{i,j}\left(t\right)={\displaystyle \frac{K_{\text{soil–root},i}\left(t\right)\cdot {\mathrm{SSF}}_{i,j}\left(t\right)\cdot \left({\mathit{\psi }}_{\mathrm{soil},j}\left(t\right)-{\mathit{\psi }}_{\mathrm{leaf},i}\left(t\right)\right)}{A_{\mathrm{soil}}\cdot \mathrm{\Delta }{Z}_j}},\end{array}$$

where, due to large axial conductances, K_soil–root was assumed to control the compensatory RWU which arises from a heterogeneously distributed soil water potential (Couvreur et al., 2012).

Finally, the tiller water oxygen isotopic composition (δ_tiller) was calculated as the average of the local soil water oxygen isotopic compositions (δ_soil) weighted by the relative distribution of positive water uptakes (i.e., not accounting for δ_soil at locations where water is exuded by the root), assuming a perfect mixture of water inside the root system (Meunier et al., 2017a):

$$\begin{array}{}\text{(10)}& {\mathit{\delta }}_{\mathrm{tiller}}={\displaystyle \frac{{\sum }_{S_j>\mathrm{0}}{S}_j\left(t\right)\cdot A_{\mathrm{soil}}\cdot \mathrm{\Delta }{Z}_j\cdot {\mathit{\delta }}_{\mathrm{soil}}\left(t\right)}{{\sum }_{S_j>\mathrm{0}}{S}_j\left(t\right)\cdot A_{\mathrm{soil}}\cdot \mathrm{\Delta }{Z}_j}}\end{array}$$

As in the experiment, δ_tiller from three plants were randomly pooled at each observation time. A total of 100 pools of three plants (possibly including several plants of the same group) were randomly selected in order to obtain the pooled simulated δ_tiller by arithmetic averaging.

The unknown parameters of the soil–root hydraulic model, i.e., the root radial conductivity (L_pr), the root axial conductance (k_axial), the soil saturated hydraulic conductivity (k_sat), and the soil tortuosity factor (λ), were finally determined by inverse modeling. For details on the procedure, the reader is referred to Appendix D.

In order to evaluate the robustness of the hydraulic model predictions (parameterized solely based on the reproduction of shoot observations in the inverse modeling scheme) from independent perspectives, we also compared predictions and measurements over four quantitative “soil–root domain” criteria: (i) the depth at which the transition between nighttime water uptake and exudation (S_i,j < 0, i.e., the release of water from the root to soil) takes place, (ii) the quantities of exuded water and the overnight increase in the soil water content, (iii) the enrichment of labeled water at the depth where the water content increase is observed overnight, and (iv) the order of magnitude of the optimal root radial conductivity value compared with data from the literature on tall fescue.

Finally, and as a comparison point, the Bayesian inference statistical model SIAR (Stable Isotope Analysis in R; Parnell et al., 2013) was used to determine the profiles of the water sink terms of 10 identified potential water sources. These water sources were defined as originating from 10 distinct soil layers (0.00–0.03, 0.03–0.07, 0.07–0.15, 0.15–0.30, 0.30–0.60, 0.60–0.90, 0.90–1.20, 1.20–1.32, 1.32–1.37, and 1.37–1.44 m) for which corresponding δ_soil values were computed (Rothfuss and Javaux, 2017). SIAR solely bases its estimates on the comparison of δ_tiller observations to the isotopic compositions of the soil water sources (δ_soil). For this, δ_tiller measurements were pooled into 12 groups corresponding to different time periods, which were selected to best reflect the observed temporal dynamics of δ_tiller. The reader is referred to Appendix E for details on the model parametrization and running procedure.

3 Results and discussion

3.1 Experimental data

This section focuses on experimental results (i) in the soil domain and (ii) in the plant domain as well as (iii) on the intercomparison of soil and plant observations.

3.1.1 Soil profiles

Figure 2a and b show a very stable soil water content profile and a more variable δ_soil profile from DaS 166 at 15:45 LT to DaS 168 at 05:00 LT. Soil was dry at the surface (0.058 m³ m⁻³ < θ < 0.092 m³ m⁻³ for the layer from 0.015 to 0.040 m), whereas it was closer to saturation at a depth of −1.30 m (θ=0.34 m³ m⁻³ ±0.012 m³ m⁻³, and the estimated θ_sat=0.40 m³ m⁻³; see Appendix A). According to the measured soil matric potentials (Fig. 2c), soil water was virtually unavailable ($\le -\mathrm{1.5}$ MPa) above a depth of −0.5 m. Soil moisture remained unchanged in the top 25 cm during the sampling period ($\mathit{\theta }=\mathrm{0.08}\pm \mathrm{0.00}$ m³ m⁻³) as well as at −1.30 m from DaS 166 at 15:45 LT to DaS 168 at 05:00 LT ($\mathit{\theta }=\mathrm{0.33}\pm \mathrm{0.01}$ m³ m⁻³), showing that roots were predominantly extracting water from deep soil layers.

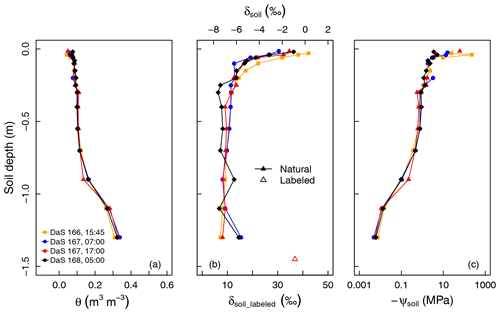
Figure 2 (a) Measured soil volumetric water content (θ), (b) oxygen isotopic composition (δ_soil), and (c) calculated soil matric potential (ψ_soil) profiles during the sampling period.

Water in the top soil layers (−0.040 m < z < −0.015 m) was isotopically enriched (−3.2 ‰ < δ_soil < 0.3 ‰) in contrast to the deepest layer (${\mathit{\delta }}_{\mathrm{soil}}=-\mathrm{7.34}$ ‰ ±0.30 ‰ at −1.30 m). Following the labeling of the reservoir water on DaS 166 at 17:00 LT, δ_soil reached a value of 36.9 ‰ at −1.50 m on DaS 167 at 17:00 LT. The development of the vegetation on DaS 166–168 (LAI =5.6) and the observed surface θ values lead us to assume that the rhizotron water losses were solely due to transpiration flux (i.e., evapotranspiration equals transpiration). The soil water oxygen isotopic exponential-shaped profiles were due to fractionating evaporation flux and, to a great extent, the fact that the soil was bare or the tall fescue cover was not fully developed in the early stages of the experiment. Therefore, the differences in the soil water oxygen isotopic profile observed on the four different sampling dates were either due to lateral heterogeneity (e.g., upper soil layers), the soil capillary rise of labeled water from the reservoir (deep soil layers), or the hydraulic redistribution of water through roots (if the isotopic composition of the redistributed water differs from that of the soil water at the release location). We noted an isotopic enrichment of 1.0 ‰ of soil water observed on DaS 168 at 05:00 LT at a depth of −0.9 m with respect to the mean δ_soil value across previous sampling dates. This could partly be due to factors such as the upward preferential flow of labeled water from the bottom soil layers and could, therefore, be a sign of the lateral heterogeneity of the soil. Another reason for this would be the hydraulic redistribution of labeled water by the roots. However, it was not possible to evaluate the relative importance of these three processes (lateral heterogeneity, capillary rise/preferential flow, and hydraulic redistribution) in the setting of the soil water isotopic profile, as the physically based soil–root model presented in section 2.4 does not account for soil liquid and vapor flow. This was also not the primary intent of the present study.

The observed RLD profile (Fig. 1a) showed a typical exponential shape, i.e., a maximum at the surface (5.42±0.34 cm cm⁻³) down to a minimum at −1.10 m (0.540±0.35 cm cm⁻³), and it increased again from the latter depth up to a value of 1.660 cm cm⁻³ at −1.30 m. This significant trend was most probably a direct consequence of the high soil water content value in this deeper layer.

3.1.2 Plant water and isotopic temporal dynamics

The temporal variation in δ_tiller (Fig. 3a) was found to be either (i) moderate during day and night, i.e., from DaS 167 at 06:00 to 11:00 LT (${\mathit{\delta }}_{\mathrm{tiller}}=-\mathrm{2.6}\pm \mathrm{1.4}$ ‰) and from DaS 167 at 21:30 LT to DaS 168 at 00:00 LT (${\mathit{\delta }}_{\mathrm{tiller}}=-\mathrm{2.7}\pm \mathrm{0.4}$ ‰), (ii) strong during the day, i.e., from DaS 167 at 11:00 to 18:00 LT (maximum value of 20.9 ‰ on DaS 167 at 12:40 LT), or (iii) strong during the night, i.e., from DaS 167 at 04:00 to 06:00 LT (maximum value of 36.4 ‰ on DaS 167 at 05:15 LT) and from DaS 168 at 00:00 to 06:00 LT (maximum value of 14.6 ‰ on DaS 168 at 04:00 LT). Note that transpiration (Fig. 3b) also occurred at night during the sampling period, due to the relatively high temperature in the glasshouse leading to a value of atmospheric relative humidity smaller than 85 % (Fig. 3b). From 12:00 to 14:00 LT and from 16:00 to 17:00 LT on DaS 167 (case ii), high values of leaf transpiration corresponded to high values of δ_tiller.

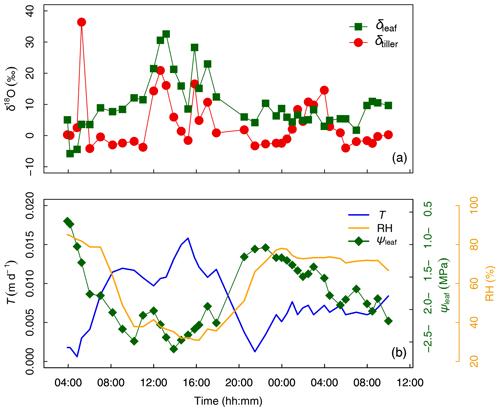
Figure 3 (a) Time series of tiller and leaf water oxygen isotopic compositions (δ_tiller and δ_leaf, respectively, ‰). (b) Transpiration flux (T, in m d⁻¹), relative humidity (HR, %), and leaf water potential (ψ_leaf, in MPa) from days after seeding (DaS) 167 at 04:00 LT to DaS 168 at 11:00 LT. Labeling was carried out on DaS 166 at 17:00 LT.

3.1.3 Partial decorrelation between water and isotopic state variables

Figure 4 shows that variables describing plant water status, i.e., T and RH (Fig. 4a) and T and ψ_leaf (Fig. 4b), were well correlated: the coefficient of determination (R²) was equal to 0.78 and 0.70 for the entire experimental duration, respectively. However, linear relationships between water status and isotopic variables were either nonexistent, e.g., between T and δ_tiller (R²=0.01, Fig. 4c) and between ψ_leaf and δ_tiller (R²=0.00, Fig. 4h), or characterized by a low R² and high p value (e.g., between T and δ_leaf, R²=0.43, p > 0.05, Fig. 4d). The partial temporal disconnect between δ_leaf and T could not be attributed to problems with the isotopic methodology during processes such as the vacuum distillation of the water from the plant tillers and leaves: the water recovery rate was always greater than 99 % and Rayleigh distillation corrections (Dansgaard, 1964; Galewsky et al., 2016) were applied to standardize the observed oxygen isotopic composition values to a 100 % water recovery (based on the comparison of the sample weight loss during distillation and the mass of collected distilled water). The evolution of δ_leaf was strongly correlated with that of δ_tiller during the day (R²=0.90), whereas it was not correlated during the night (R²=0.00, Fig. 4j). These observed correlations are in agreement with the Craig and Gordon (1965) model revisited by Dongmann et al. (1974) and later by Farquhar and Cernusak (2005) and Farquhar et al. (2007). The model, which is extensively used in the current literature (e.g., Dubbert et al., 2017), states that, at isotopic steady-state, δ_leaf is a function of the input water oxygen isotopic composition (δ_tiller) among other variables, i.e., leaf temperature (not measured during the experiment), stomatal and boundary layer conductances, oxygen isotopic composition of atmospheric water vapor, and relative humidity.

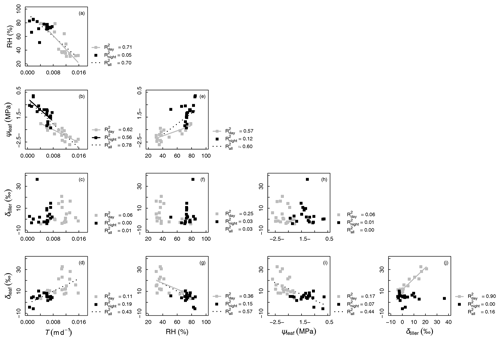
Figure 4 Correlations between measured variables: oxygen isotopic compositions of xylem and leaf waters (δ_tiller and δ_leaf, respectively, in ‰), transpiration rate (T, in m d⁻¹), relative humidity (RH, %), and leaf water potential (ψ_leaf, in MPa). The coefficients of determination (R² values) are reported for all data as well as separately for “day” (gray symbols) and “night” data (black symbols; see Appendix C for definition of “day” and “night” experimental periods). Regression lines are drawn for linear models with a p value < 0.01

It is generally difficult to observe a statistically significant δ_leaf−δ_tiller (Fig. 4j) relationship at this temporal scale under natural abundance conditions in the field, as the soil water isotopic weak gradient translates into weaker δ_tiller temporal dynamics. The quality of the linear fit between δ_leaf and δ_tiller data collected during the day (R²=0.90) was made possible in this specific experiment by the artificial isotopic labeling pulse that enhanced the soil water isotopic gradient, which in turn increased the range of variation in δ_tiller, ultimately highlighting the δ_leaf−δ_tiller temporal correlation. Air relative humidity is a driving variable of δ_leaf in the model of Dongmann et al. (1974) via the competing terms of (1− RH) ⋅δ_tiller and RH ⋅δ_atm, where δ_atm is the atmospheric water vapor isotopic composition inside the glasshouse. An overall significant linear correlation was observed between RH and δ_leaf during the experiment (R²=0.57, Fig. 4g). During the two night periods (i.e., from 04:00 to 06:00 LT and from 20:30 to 07:00 LT), as relative humidity increased in the glasshouse (51 % < RH < 85 %, Fig. 3b), the influence of the isotopic labeling of the tiller water (due to the labeling of deep soil water) via the (1− RH) ⋅δ_tiller term decreased to the benefit of the RH ⋅δ_atm term (with δ_atm values ranging from −15.9 to −10.7 ‰ and a mean of $-\mathrm{13.1}\pm \mathrm{1.6}$ ‰, data not shown). This was especially visible between 04:50 and 06:00 LT on DaS 167 and between 01:00 and 06:00 LT on DaS 168, when δ_tiller reached greater values than δ_leaf.

From a different perspective, as three plant water samples were pooled to reach a workable volume for the isotopic analysis at each observation time without replicates, the isotopic signal fluctuations may reflect both its temporal dynamics and its variability within the plant population.

3.2 Simulations

This section focuses on modeling results with (i) an explanation of the variability of plant and soil observations, (ii) an independent validation of model predictions, (iii) a discussion of possible sources of variability not accounted for by the model, and (iv) a comparison of physical and Bayesian model outputs.

3.2.1 Rooting depth and transpiration rate control δ_tiller and ψ_leaf fluctuations, respectively

Despite the use of a global optimizer and 4 degrees of freedom (L_pr, k_axial, k_sat, and λ, see optimal values in Table 1) that specifically aimed at matching the simulated and observed temporal dynamics of δ_tiller, none of the 60 root system groups or the average population could reproduce the measured fluctuations in time (R²=0.00, Fig. 5a), regardless of the weight attributed to this criterion in the objective function. The predicted versus the observed δ_tiller distributions including all plant groups and observation times differed noticeably but not significantly (6.6±8.4 ‰ and 3.7±8.4 ‰, respectively) when pooling three simulated δ_tiller randomly at each observation time (P > 0.01 in 92 cases out of 100 repeated drawings), as in the measurements. In addition, the simulated ψ_leaf fitted the observations well (R²=0.67, with overall distributions of $-\mathrm{0.175}\pm \mathrm{0.053}$ MPa and $-\mathrm{0.177}\pm \mathrm{0.053}$ MPa, respectively; Fig. 5c). When analyzing the distributions of ψ_leaf and δ_tiller per maximum root system depth (Fig. 5b, d), it appears that the ψ_leaf signal is not sensitive to the rooting depth (Fig. 5d), whereas δ_tiller is more sensitive to rooting depth than to the temporal evolution of the plant environment (Fig. 5b).

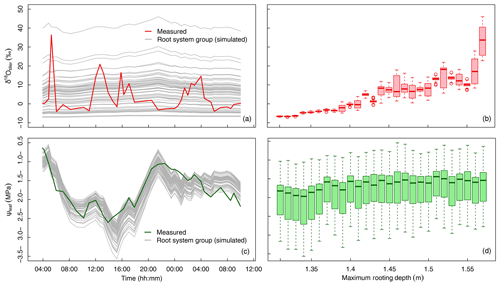
Figure 5 Variation in δ_tiller and ψ_leaf in time and across the 60 groups of simulated root systems. (a) The measured (thick red line) and simulated (thin gray lines, one line per root system group, following a “swarm” pattern) temporal dynamics of δ_tiller. (b) Boxplot of simulated δ_tiller values for each root system maximum depth, in 1 cm increments. (c) The measured (thick green line) and simulated (thin gray lines, one line per root system group, following a “roller-coaster” pattern) temporal dynamics of ψ_leaf. (d) Boxplot of simulated ψ_leaf values for each root system maximum depth, in 1 cm increments.

Table 1 Optimum and limits of the four-dimensional parametric space explored by the global optimization algorithm aiming at minimizing the difference between simulated and observed δ_tiller and ψ_leaf, as well as their standard deviation from average values during the full experiment.

This leaves us with two hypotheses. First, the “roller-coaster hypothesis” states that δ_tiller rapidly goes up and down with all individuals onboard the same car (i.e., little variability within the population, unlike the predictions in Fig. 5a but similar to the simulated ψ_leaf in Fig. 5c). If this holds true, the physical model lacks a process that would capture the observed temporal fluctuations of δ_tiller. Second, the “swarm pattern hypothesis” states that δ_tiller is rather stable in time, but its values within the plant population are dispersed like a flying swarm; thus, δ_tiller values sampled at different times fluctuate, not due to temporal dynamics but instead owing to the fact that different individuals are sampled (Fig. 5a).

The model suggests that the tall fescue population ψ_leaf follows a “roller-coaster” dynamics that is driven by transpiration rate, whereas the population δ_tiller follows a “swarm” pattern that is driven by the maximum rooting depth of the sampled plants. As no correlation could be expected between the drivers (the maximum rooting depth of the sample plants and the canopy transpiration rate), our analysis explains the absence of a correlation between δ_tiller and ψ_leaf or transpiration rate.

In future experiments and in the specific context of labeling pulses, sampling more plants at each observation time would help disentangle the spatial from the temporal sources of variability of ψ_leaf and δ_tiller. However, it would be at the cost of the temporal resolution of observations or would necessitate a larger setup with more plants in the case of controlled conditions experiments.

3.2.2 Independent observations support the validity of the hydraulic model predictions

In the last 12 h of the experiment (DaS 167 at 17:00 LT to DaS 168 at 05:00 LT), the measured soil water content increased by 0.029 m³ m⁻³ at a depth of −0.9 m, which could be a sign of nighttime hydraulic redistribution. During the same period, the physical model predicted a cumulative water exudation sufficient to increase soil water content by 0.003 m³ m⁻³, as the soil water potential was low enough to generate reverse flow but high enough not to disrupt the hydraulic continuity between the soil and roots (Carminati and Vetterlein, 2013; Meunier et al., 2017a). While this increase is smaller than the observed water content change, it is only a component in the soil water mass balance. Given the soil water potential vertical gradient, upward soil capillary water flow may have accounted for another part of the observed moisture change. Experimental observations also show that δ_soil increased by 1.0 ‰ at a depth of −0.9 m during that time (−6.2 ‰, which was a value significantly higher than −7.1 ‰ ±0.1 ‰ at earlier times based on an ANOVA analysis, P < 0.01), whereas our simulations of hydraulic redistribution generated a 0.34 ‰ increase of δ_soil. As soil capillary flow may not generate local maxima of δ_soil (no enrichment observed at surrounding depths, see Fig. 2b), and soil evaporation is assumed negligible at that depth, it is likely that the observed local enrichment was entirely due to hydraulic redistribution, which would then be underestimated by a factor of about 3 in our simulations. Increasing water exudation by a factor 3 would imply a simulated water content change due to exudation of 0.0090 m³ m⁻³ absolute water content, which remains compatible with the experimental observation. Between a depth of −1.1 m and −0.9, the nighttime water flow pattern transitioned from exudation to uptake in both measurements and predictions. At −1.1 m, the model predicted a cumulative water uptake sufficient to decrease the soil water content by 0.0101 m³ m⁻³, compared with the observed 0.0141 m³ m⁻³ total soil water content decrease. The remaining 0.004 m³ m⁻³ water content decrease may have contributed to the recharge of the soil layers above via capillary flow, which was not simulated. Therefore, all relevant measurements (local increase in soil water content and local enrichment of water isotopic composition) and simulation results (S < 0, i.e., local water release from roots) clearly converge to the conclusion that hydraulic lift occurred in the vicinity of a depth of −0.9 m in the early morning of DaS 168.

As far as fitted parameter values are concerned, L_pr ($\mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{7}}$ m MPa⁻¹ s⁻¹) was in the range found by Martre et al. (2001) for tall fescue (${\mathrm{2.210}}^{-\mathrm{7}}\pm \mathrm{0.1}$ m MPa⁻¹ s⁻¹) and also falls in the range obtained by Meunier et al. (2017a) for another grass (Lolium multiflorum Lam., $\mathrm{6.8}\times {\mathrm{10}}^{-\mathrm{8}}$ to $\mathrm{6.8}\times {\mathrm{10}}^{-\mathrm{7}}$ m MPa⁻¹ s⁻¹). Our k_axial value cannot be compared to values of axial root conductance from the literature, as it transfers the water absorbed by roots in a single “big root” per group of five identical plants. The optimal value of k_sat was quite high (Table 1) but reportedly very correlated with λ (i.e., soil unsaturated hydraulic conductivity is proportional to k_sat but also to $S_e^{\mathit{\lambda }}$; van Genuchten, 1980), so that the low value of the latter compensated for the high value of the former; thus, they should be considered as effective rather than physical parameters.

3.2.3 Other sources of variability and observational error

Our treatment of the soil medium in this experiment (sieving and irrigation from the bottom) makes it laterally more homogeneous than natural soils. This method allowed us to specifically study the impact of the vertical gradients of δ_soil on δ_tiller. It also justified the use of a simplistic one-dimensional model adapted to the vertically resolved measurements. If lateral heterogeneity of soil water content remained and was accounted for, our predictions of root water uptake distribution, δ_tiller, and ψ_leaf would be altered. Observational errors in the gravimetric soil water content measurement (converted to soil water potential using the soil water retention curve) would also alter these predictions. In order to quantify the sensitivity of our simulated results to such heterogeneity or observational error, we varied the soil water content input by ±0.02 m³ m⁻³ at three critical depths (−0.9, −1.1, and −1.3 m, before interpolation) at the last observation time, during which measurements and simulations suggested that hydraulic lift occurred. Our results were mostly sensitive to soil water content alterations at −0.9 m, and they barely differed in response to alterations at −1.1 and −1.3 m, although the conclusions were not affected qualitatively. No statistically significant difference between the predicted and observed δ_tiller distributions for the overall dataset could be found when pooling three simulated δ_tiller randomly at each observation time (predicted and observed δ_tiller distributions were closest to differing when the soil water content was reduced by 0.02 m³ m⁻³ at a depth of 0.9 m; P > 0.01 in 76 cases out of 100 repeated drawings). Measured and simulated ψ_leaf remained very correlated in all cases (from an R² value of 0.69 to 0.74 when adding or removing 0.02 m³ m⁻³ at a depth of 0.9 m, respectively). Furthermore, when adding or removing 0.02 m³ m⁻³ at a depth of 0.9 m, cumulative water exudation at −0.9 m varied between 0.0019 and 0.0035 m³ m⁻³, uptake at −1.1 m varied between 0.0080 and 0.0108 m³ m⁻³, and the simulated change in the δ_soil ranged between 0.28 and 0.40 ‰, respectively.

Lateral heterogeneity in the soil water isotopic composition may as well occur at the microscopic scale. As water in micropores is less mobile than water in meso- and macropores (Alletto et al., 2006), it is likely that, in the lower half of the profile, the capillary rise of labeled water affected the composition of water in meso- and macropores more than in micropores. If roots have more access to meso- and macropore water, then the water absorbed by roots would be isotopically enriched compared with the “bulk soil water” characterized experimentally. The importance of this possible bias depends on soil texture and heterogeneity (e.g., the existence of more isolated “pockets” of soil or compact clusters) as well as on the speed of water mixing between mobile and immobile water fractions (Gazis and Feng, 2004). Including this process in the modeling would necessitate sufficient observations to estimate the aforementioned properties and ideally some quantification of the lateral heterogeneity of the soil water isotopic composition at the microscale.

The lateral heterogeneity of soil hydraulic properties and root distribution may also have participated in the generation of lateral soil water potential heterogeneities, particularly in undisturbed soils. If one had access to data on the lateral heterogeneity of soil properties and rooting density, it would be possible to simulate three-dimensional soil–root water flow with a tool such as R-SWMS (modeling “Root-Soil Water Movement and Solute transport”; Javaux et al., 2008), using a randomization technique for soil properties' distribution as in Kuhlmann et al. (2012), in order to obtain estimations of the relative importance of this type of heterogeneity on δ_tiller and ψ_leaf variability.

Unlike the tiller water isotopic composition, the leaf water potential turned out to be very sensitive to the transpiration rate in our simulations (see temporal fluctuations of gray lines in Fig. 5c) and not very sensitive to the root distribution (see small variations in leaf water potential across individuals in Fig. 5d). In this setup, this suggests that the hydraulic conductance of the soil–root system limited the shoot water supply more than the distribution of roots, as in Sulis et al. (2019). Simulated baseline (i.e., for uniform transpiration rates) leaf water potentials are shown as gray lines in Fig. 5c, and measured leaf water potentials are shown as a green line in the same panel. The fact that they match well, despite the high sensitivity of the leaf water potential to the transpiration rate, reinforces the idea that the transpiration rate was likely not spatially heterogeneous among the plant population. Therefore, the tiller water isotopic composition, whose sensitivity to the transpiration rate is already very low, was likely not affected by transpiration rate heterogeneity.

3.2.4 Do root water uptake profiles predicted by hydraulic and Bayesian models differ?

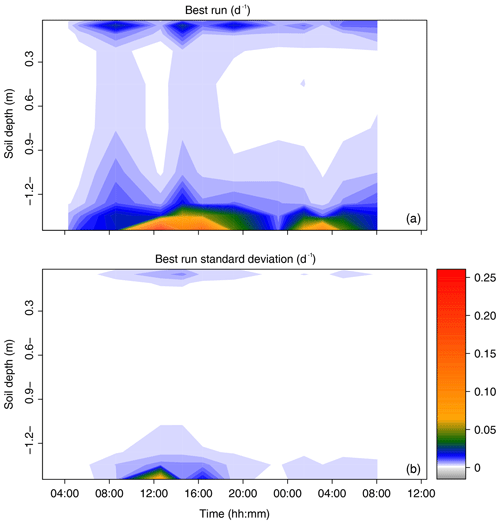
The root water uptake dynamics predicted by the mechanistic model are shown in Fig. 6a. The overall pattern of peaking water uptake in the lower part of the profile during daytime matched that of the statistical model, and the correlation coefficient of both model predictions was relatively high (R²=0.53) on average over the simulation period (see Fig. 7). The main differences were as follows: (i) in the upper soil layers where the soil water potential was lower than −1.5 MPa, the statistical model predicted water uptake, which is theoretically impossible given the leaf water potential above −0.4 MPa (van Den Honert, 1948); (ii) in the upper half of the profile, the physical model predicted exudation at a rate limited by the low hydraulic conductivity between the root surface and the bulk soil, with a peak at night, at a depth of −0.9 m (quantitative analysis in previous section); (iii) below a depth of −1.0 m, the water uptake rate predicted by the statistical model steadily increased with depth while that of the physical model was more uniform, likely due to axial hydraulic limitation (e.g., Bouda et al., 2018) counteracting the increasing soil water potential with depth. Note that the outcome of the statistical model may significantly depend on the definition of the a priori relative RWU (rRWU) profile. In the present study, we set it to follow a “flat” uniform distribution (i.e., rRWUj $=\mathrm{1}/\mathrm{10}$; see Appendix E); in other words, each layer was initially defined to contribute equally to RWU. Contrary to other studies (e.g., Mahindawansha et al., 2018), where the a priori rRWU profile was empirically constructed on the basis of soil water content and root length density profiles, we decided not to further arbitrarily constrain the Bayesian model for the sake of comparison with the physically based soil–root model.

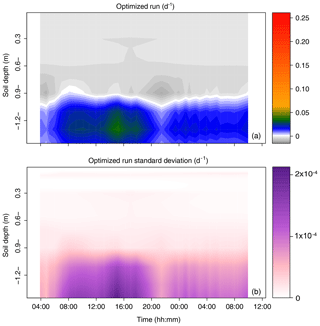
Figure 6 Time series of the profiles of root water uptake per unit soil volume (sink term, d⁻¹) computed with the physically based model. (a) Sum of sink terms across the 60 groups of the population. (b) Variability of the sink terms within the 60 groups of the population (1 standard deviation).

Figure 7 Time series of the profiles of root water uptake per unit soil volume (sink term, d⁻¹) computed with the statistical model SIAR (a). Panel (b) reports the variance of the estimated sink term (1 standard deviation).

3.3 Progress and challenges in soil water isotopic labeling for RWU determination

Often, in the field, the vertical dynamics of both soil water oxygen and hydrogen isotopic compositions are not strong enough (or show convolutions leading to issues of identifiability) for partitioning RWU among different contributing soil water sources. As a consequence, we unfortunately cannot make use of the natural variability in isotopic abundances for deciphering soil–root transfer processes (Beyer et al., 2018; Burgess et al., 2000). To address this limitation of the isotopic methodology, labeling pulses have been applied locally at different depths in the soil profile (e.g., Beyer et al., 2016) or at the soil upper/lower boundaries under both laboratory and field conditions by mimicking rain events Piayda (e.g., Piayda et al., 2017) and/or rise of the groundwater table (Meunier et al., 2017a; Kühnhammer et al., 2019).

After labeling, we are faced with two problems. First, the labeling pulse might enhance RWU at the labeling location if the volume of added water significantly changes the value of soil water content. This, therefore, poses the question of the meaningfulness of the derived RWU profiles, irrespective of the model used (i.e., physically based soil–root model or statistical multisource mixing model). In other words, are we observing natural RWU behavior of the plant individual or population or are we seeing the influence of the labeling pulse? Thus, a way to move forward is the utilization of environmental observatories such as ecotrons and field lysimeters (e.g., Groh et al., 2018; Benettin et al., 2018) that provide the means to better constrain hydraulic boundary conditions and reduced their isotopic heterogeneity. They allow for a mechanistic and holistic understanding of soil–root processes from stable isotopic analysis.

Second, the difficulty to properly observe the propagation of the labeling pulse in the soil after application and the temporal dynamics of the plant RWU isotopic composition in situ is also problematic. Beyer and Dubbert (2019) presented a comprehensive review on recent isotopic techniques for nondestructive, online, and continuous determination of soil and plant water isotopic compositions (e.g., Rothfuss et al., 2013; Quade et al., 2019; Volkmann et al., 2016a) as alternatives to the widely used combination of destructive sampling and offline isotopic analysis following cryogenic vacuum extraction (Orlowski et al., 2016) or liquid–vapor direct equilibration (Wassenaar et al., 2008). These techniques have the potential for a paradigm change in isotopic studies on RWU processes so that, for example, isotopic effects during sample collection are fully understood.

The present study highlights that the isotope data alone should not be “trusted” and should always be complemented by information on environmental factors as well as soil and plant water status in order to go beyond the simple application of statistical models. This is especially the case in the framework of labeling studies where strong soil water isotopic gradients may induce strong dynamics of the RWU isotopic composition from a low variability of rooting depths.

4 Conclusion

In the present study, light could be shed on RWU of Festuca arundinacea by specifically manipulating the lower boundary conditions for water content and oxygen isotopic composition. The new version of the one-dimensional model of Couvreur et al. (2014) implemented here accounted for both root and soil hydraulics in a population of “big” root systems of known root length density profile. This approach underlined the high sensitivity of δ_tiller to rooting depth and suggested that if δ_tiller is measured on a limited number of individuals, its variations in time may reflect the heterogeneity of the rooting depth within the population rather than temporal dynamics, which was minor in our simulations. The model avoided the prediction of water uptake at locations where it was physically unavailable (e.g., in the top half of the soil profile), by accounting for water potential differences observed between the leaves and the soil, and quantitatively explained the local isotopic enrichment of soil water as the occurrence of nighttime hydraulic lift at a depth of −0.9 m. Conversely, the Bayesian statistical approach tested for comparison, which was driven solely by isotopic information, naturally translated the observed changes of δ_tiller into profound temporal dynamics of RWU at the expense of ecophysiological considerations (e.g., the temporal dynamics of leaf water potential and transpiration rate).

This case study highlights the potential limitations of water isotopic labeling techniques for studying RWU: the soil water isotopic artificial gradients induced from water addition result in an improvement in RWU profiles' determination such that they are properly characterized spatially and temporally. As already pointed out in the review of Rothfuss and Javaux (2017), this study also underlines the interest of complementing in situ isotopic observations in soil and plant water with information on soil water status and plant ecophysiology. Furthermore, this work calls for the use of simple soil–root models (although they require additional water status measurements and make more explicit assumptions on the description of the soil–plant system than the traditional Bayesian approach) for inversing isotopic data and gaining insights into the RWU process.

Appendix A

Figure A1 Soil macro-rhizotron experimental setup with tall fescue cover.

Appendix B

Table B1 Soil retention curve and parameters' optimized values (van Genuchten, 1980 – Burdine; Meunier et al., 2017a).

Appendix C

Table C1 Timeline of the destructive sampling. DaS stands for “day after seeding”. The “day” periods are from 07:00 to 17:50 LT on DaS 167 and from 07:00 to 10:00 LT on DaS 168. The “night” periods are from 03:55 to 06:00 LT on DaS 167 and from 20:30 to 06:00 LT on DaS 167–168.

Appendix D: Inverse modeling scheme

The parametrization method used in this study was inverse modeling, and there were four targets: (i) minimizing the differences between observed and predicted δ_tiller in each pool (p), (ii) minimizing the difference between the standard deviations of observed and predicted δ_tiller (temporal and population deviations combined), (iii) minimizing the differences between observed and predicted ψ_leaf in each root system group (i), and (iv) minimizing the difference between the standard deviations of observed and predicted δ_tiller (temporal and population deviations combined). These targets were translated into an objective function (OF) to be minimized, where the differences were normalized by the standard deviation (SD) of the observations in order to make the error function dimensionless:

$$\begin{array}{}\text{(D1)}& \begin{array}{rl}& \mathrm{OF}=\\ & \sqrt{{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}({\displaystyle \frac{\mathrm{1}}{N_{\mathrm{p}}{N}_{\mathrm{t}}}}{\sum }_i{\sum }_t{\left({\displaystyle \frac{{\mathit{\delta }}_{\mathrm{tiller},\mathrm{obs}}\left(t\right)-{\mathit{\delta }}_{\mathrm{tiller},\mathrm{p},\mathrm{sim}}\left(t\right)}{\mathrm{SD}\left({\mathit{\delta }}_{\mathrm{tiller},\mathrm{obs}}\right(t\left)\right)}}\right)}^{\mathrm{2}}}\stackrel{\mathrm{‾}}{+{\displaystyle \frac{\mathrm{1}}{N_i{N}_{\mathrm{t}}}}{\sum }_i{\sum }_t{\left({\displaystyle \frac{{\mathit{\psi }}_{\mathrm{leaf},\mathrm{obs}}\left(t\right)-{\mathit{\psi }}_{\mathrm{leaf},\mathrm{i},\mathrm{sim}}\left(t\right)}{\mathrm{SD}\left({\mathit{\psi }}_{\mathrm{leaf},\mathrm{obs}}\right(t\left)\right)}}\right)}^{\mathrm{2}})}\\ & +\left|{\displaystyle \frac{\mathrm{SD}\left({\mathit{\delta }}_{\mathrm{tiller},\mathrm{obs}}\left(t\right)\right)-\mathrm{SD}\left({\mathit{\delta }}_{\mathrm{tiller},\mathrm{p},\mathrm{sim}}\left(t\right)\right)}{\mathrm{SD}\left({\mathit{\delta }}_{\mathrm{tiller},\mathrm{obs}}\left(t\right)\right)}}\right|\\ & +\left|{\displaystyle \frac{\mathrm{SD}\left({\mathit{\psi }}_{\mathrm{leaf},\mathrm{obs}}\left(t\right)\right)-\mathrm{SD}\left({\mathit{\psi }}_{\mathrm{leaf},\mathrm{i},\mathrm{sim}}\left(t\right)\right)}{\mathrm{SD}\left({\mathit{\psi }}_{\mathrm{leaf},\mathrm{obs}}\left(t\right)\right)}}\right|,\end{array}\end{array}$$

where N_p is the number of δ_tiller pools simulated (100) at each observation time, N_i is the number of plant groups simulated (60), and N_t is the total number of observation times (40).

The global optimizer multistart heuristic algorithm OQNLP (Optimal Methods Inc.) from the MATLAB (MathWorks, Inc., USA) optimization toolbox was used to minimize the error function within the lower and upper limits of the parametric space reported in Table 1.

Appendix E: Statistical determination of relative RWU profiles with SIAR

The Bayesian inference statistical model SIAR (Parnell et al., 2013) was used to determine the profiles of relative contributions of 10 identified potential water sources to RWU (rRWU, dimensionless). These water sources were defined as originating from the following soil layers: 0.00–0.03, 0.03–0.07, 0.07–0.15, 0.15–0.30, 0.30–0.60, 0.60–0.90, 0.90–1.20, 1.20–1.32, 1.32–1.37, and 1.37–1.44 m. Their corresponding isotopic compositions were obtained from the measured soil water isotopic compositions (δ_soil) and volumetric content (θ) values following Eq. (E1) (Rothfuss and Javaux, 2017):

$$\begin{array}{}\text{(E1)}& {\mathit{\delta }}_{\mathrm{soil},J}={\displaystyle \frac{{\sum }_{j\in J}{\mathit{\delta }}_{\mathrm{soil},j}\cdot {\mathit{\theta }}_j\cdot \mathrm{\Delta }{Z}_j}{{\sum }_{j\in J}{\mathit{\theta }}_j\cdot \mathrm{\Delta }{Z}_j}},\end{array}$$

where J is the soil layer index, j is the soil sub-layer index, and ΔZ_j is the thickness of the soil sub-layer j. Therefore, Eq. (E1) translates the soil water isotopic composition measured across sub-layers j into representative isotopic compositions of the different sources (i.e., across layers J). The computed δ_soil,J values were compared to δ_tiller values. For this comparison, δ_tiller measurements were pooled into 12 groups corresponding to different time periods. These groups were defined to best reflect the apparent temporal dynamics of δ_tiller.

For each of the 12 time periods the following actions were undertaken:

• i.

  the “siarmcmcdirichletv4” function of the SIAR R package (https://cran.r-project.org/web/packages/siar/index.html, last access: 15 August 2019) was run 500 000 times with prescribed burnin and thinby equal to 50 000 and 15, respectively, and the output of the model (i.e., the a posteriori rRWU distribution across the 10 soil water sources, J) was obtained from a flat Dirichlet a priori rRWU distribution (i.e., rRWU${}_J=\mathrm{1}/\mathrm{10}$);

  [ii.] the “best run” (br, dimensionless) was selected from SIAR's output. It was defined as the closest solution of the relative contributions across sources from the set of most frequent values (mfv, dimensionless), i.e., the relative contribution with the greatest probability of occurrence. The best run was identified as minimizing the objective function shown below, i.e., the RMSE (root mean square error) with respect to the set of mfv_J:

  $$\begin{array}{}\text{(E2)}& \mathrm{OF}=\sqrt{{\displaystyle \frac{{\sum }_{J=\mathrm{1}}^{\mathrm{10}}({\mathrm{mfv}}_J-b{r}_J{)}^{\mathrm{2}}}{\mathrm{10}}}}\end{array}$$
• iii.

  br was then multiplied by the transpiration rate (in m d⁻¹) and divided by the soil layer thicknesses (ΔZ_J, in m) to obtain the sink terms (S_J, i.e., root water uptake rate per unit soil volume, expressed in d⁻¹). The interest of sink terms in a comparison is that they do not vary with soil vertical discretization.

Steps (i)–(iii) were repeated 1000 times to estimate the variance in the best run for each time period and soil water source J.

Appendix F: List of variables with symbols and units

Name	Symbol	Units
Leaf water potential/head	ψleaf	(MPa)
Soil water potential/head	ψsoil	(MPa)
Water volumetric mass	ρw	(kg m−3)
Soil apparent density	ρb	(kg m−3)
Soil gravimetric water content	θgrav	(kg kg−1)
Soil volumetric water content	θ	(m3 m−3)
Intensity of water uptake (sink term)	S	(d−1)
Transpiration rate per unit soil area	T	(m d−1)
Air relative humidity	RH	%
Soil horizontal area	Asoil	(m2)
Soil layer depth (for each layer)	z	(m)
Soil layer thickness (for each layer)	ΔZ	(m)
Root length (for each soil layer)	lroot	(m)
Relative root water uptake	rRWU	(Dimensionless)
Best run	br	(Dimensionless)
Root length density	RLD	(m m−3)
Soil water oxygen isotopic composition	δsoil	(‰)
Tiller water oxygen isotopic composition	δtiller	(‰)
Leaf water oxygen isotopic composition	δleaf	(‰)
Soil–root system conductance	Ksoil–root	(m3 MPa−1 s−1)
Soil–root radial conductance	Kradial	(m3 MPa−1 s−1)
Root radial conductivity	Lpr	(m MPa−1 s−1)
Root axial conductance	Kaxial	(m3 MPa−1 s−1)
Equivalent root axial conductivity	kaxial	(m4 MPa−1 s−1)
Soil hydraulic conductivity	ksoil	(m2 MPa−1 s−1)
Saturated soil hydraulic conductivity	ksat	(m2 MPa−1 s−1)
Soil hydraulic conductivity parameter	λ	(Dimensionless)
Soil relative water content	Se,j	(Dimensionless)