the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Turbulence in the stratified boundary layer under ice: observations from Lake Baikal and a new similarity model
Ilya Aslamov
Vladimir Kozlov
Roman Zdorovennov
Nikolai Granin
Seasonal ice cover on lakes and polar seas creates seasonally developing boundary layer at the ice base with specific features: fixed temperature at the solid boundary and stable density stratification beneath. Turbulent transport in the boundary layer determines the ice growth and melting conditions at the ice–water interface, especially in large lakes and marginal seas, where large-scale water circulation can produce highly variable mixing conditions. Since the boundary mixing under ice is difficult to measure, existing models of ice cover dynamics usually neglect or parameterize it in a very simplistic form. We present the first detailed observations on mixing under ice of Lake Baikal, obtained with the help of advanced acoustic methods. The dissipation rate of the turbulent kinetic energy (TKE) was derived from correlations (structure functions) of current velocities within the boundary layer. The range of the dissipation rate variability covered 2 orders of magnitude, demonstrating strongly turbulent conditions. Intensity of mixing was closely connected to the mean speeds of the large-scale under-ice currents. Mixing developed on the background of stable density (temperature) stratification, which affected the vertical structure of the boundary layer. To account for stratification effects, we propose a model of the turbulent energy budget based on the length scale incorporating the dissipation rate and the buoyancy frequency (Dougherty–Ozmidov scaling). The model agrees well with the observations and yields a scaling relationship for the ice–water heat flux as a function of the shear velocity squared. The ice–water heat fluxes in the field were the largest among all reported in lakes (up to 40 W m−2) and scaled well against the proposed relationship. The ultimate finding is that of a strong dependence of the water–ice heat flux on the shear velocity under ice. The result suggests large errors in the heat flux estimations when the traditional “bulk” approach is applied to stratified boundary layers. It also implies that under-ice currents may have much stronger effect on the ice melt than estimated by traditional models.
- Article
(6389 KB) - Full-text XML
- BibTeX
- EndNote
The demand for a better quantitative description of the formation, evolution, and decay of seasonal ice has grown recently because of large-scale trends toward a shortening ice season in the Northern Hemisphere and the drastic decrease of the Arctic sea ice extent. Closure of the global mass budget of the Arctic seasonal ice is a complex problem, related, apart from the atmospheric and terrestrial heat sources, to the upward transport of heat stored in the under-ice water body. An important role in the heat budget of seasonal ice is played by the storage of the solar radiation in the under-ice water, which is subsequently transported to the ice base by the under-ice currents. The effect of currents on ice melt is particularly apparent in the Arctic ocean, where the loss of ice mass in spring and summer occurs mainly from the ice bottom (McPhee, 1992; Perovich et al., 2011; Carmack et al., 2015; Peterson et al., 2017). Apart from the polar oceans and seas, seasonal formation of ice cover is an essential feature of high-latitude freshwater lakes. Physics of seasonal ice cover on lakes has gained particular attention, as an essential part of climate change research (Magnuson et al., 2000; Kirillin et al., 2012). A shorter seasonal ice cover as a result of global warming may produce a positive feedback due to increase of greenhouse gas emission and changing the global carbon budget (Tranvik et al., 2009). Hence, estimation of the consequences of phenological changes on inland waters requires quantification of the physical mechanisms that control the formation and melting of ice. The heat and mass transfer at the ice–water interface (IWI) is the least studied among these mechanisms (Kirillin et al., 2012; Aslamov et al., 2014a).
The seasonal ice cover on lakes, especially on large ones, shares many basic features with the seasonal sea ice. Storage of the heat from solar radiation in the surface mixed layer (SML) and its subsequent release to the ice base is the major mechanism of the ice cover melt in lakes (Kirillin et al., 2012) as well as in the ocean (Perovich and Richter-Menge, 2009). However, in contrast to seawater, lakes possess some specific physical features affecting formation and melting of ice. Water temperatures in ice-covered freshwater lakes are below their value of maximum density. Therefore, solar heating of upper layers produces free convection, which is the major mechanism of the SML formation (Mironov et al., 2002). In addition to the storage of the heat from the short-wave radiation penetrating the ice, convective mixing in the SML entrains the warmer water from the deep layers (Kirillin et al., 2012). The convective SML is separated from the ice base by a stably stratified interfacial layer (IL) with an upward temperature drop down to the freezing point of freshwater. At low salinities, water temperatures remain always higher than that of ice. Hence the IL with a downward temperature increase always exists under the ice base; its thickness depends on the strength of radiative heating and the temperature of the SML underneath (Barnes and Hobbie, 1960). The strong stratification in the IL prevents convective mixing despite the negative buoyancy production by the decrease of the solar radiation with depth and reduces convective transport of heat to the ice–water interface. As a result, only a small amount of the heat is available for ice melt, despite strong convection in the SML (Kirillin et al., 2018). The situation is akin to formation of a stably stratified layer (SL) beneath the ice base and the near-surface temperature maximum in marginal polar seas, driven by freshening of the surface waters due to runoff or accelerated sea ice melt (Jackson et al., 2010, 2012).
The ice–water interaction becomes more complex when a freshwater lake becomes essentially large compared to the Rossby radius of deformation (Gill, 1982). The condition suggests long-lasting water circulation under ice, which, similarly to the ocean circulation, is able to produce significant velocity shear at the ice base and thus accelerate the upward heat transport (McPhee, 1992). Among such lakes, Lake Baikal – the largest lake by volume on earth – most closely resembles the Arctic Ocean with regard to seasonal ice dynamics. Thanks to the strong winter cooling under the influence of the Siberian atmospheric pressure maximum, Lake Baikal has steady ice cover over the entire lake for 3–5 months of the year. Consequently, the seasonal ice regime plays a crucial role in hydrodynamics and ecosystem functioning of the lake. Aslamov et al. (2014a, b) reported high water-to-ice heat fluxes in Lake Baikal during the period of ice growth. The fluxes were apparently related to the surface water circulation pattern beneath the ice cover (Zhdanov et al., 2017). The observed ice-to-water heat fluxes exceeded fluxes measured in small lakes (Kirillin et al., 2018) by up to an order of magnitude. Free convection due to penetrating solar radiation was not strong enough to produce upward heat release at these rates. Hence, the high turbulence level was tentatively attributed by the authors to the shear mixing produced by the water circulation under the ice surface.
The intensity of turbulence produced by velocity shear in the boundary layer and the resulting heat transport from water to the ice base may vary depending on the current velocity, ice structure, and density stratification under ice. In order to estimate the effect of under-ice circulation on the ice–water heat flux in lakes, we performed a field experiment combining temperature measurements with high temporal and vertical resolution within the ice cover and fine-scale registration of current velocities under the ice base. The temperature observations were subsequently used for estimation of the heat budget at the ice–water interface and derivation of the ice–water heat fluxes. The data on fine-scale velocity fluctuations provided information on variability of mean currents under ice as well as on the characteristics of turbulent mixing in the ice–water boundary layer in the form of the dissipation rate of the turbulent kinetic energy (TKE). Below, both outcomes of the field experiment are combined to analyze the characteristics of the turbulent boundary layer and to analyze the effect produced by turbulent mixing on the ice cover thickness. The overarching goal of the presented study is to establish the scaling relationships linking the under-ice circulation with the seasonal ice cover dynamics and suitable for parameterization of the ice–water heat exchange in regional and global models of seasonal ice.
To a good approximation, the base of the lake ice can be represented as a rigid boundary on top of a fluid; i.e., the vertical heat transport at the ice–water interface is close to being purely conductive on both ice and water sides, governed by molecular forces within the ice cover and within a thin “conduction” layer of water. It should be noted that the assumption generally holds true for solid freshwater ice with a small amount of impurities: Saltwater ice undergoes brine extraction, which can induce convection by mass flux at the boundary and markedly increase the heat transport. Similarly, the increase of water flow can destroy the conduction layer at the ice–water interface in “rotten” freshwater ice subject to internal melting, especially in the presence of impurities (Bluteau et al., 2017). In the majority of freshwater lakes, the aforementioned effects are negligible during most of the ice season. In particular, in Lake Baikal, due to cold winters and low snow precipitation, practically 100 % of the ice cover consists of clear congelation (“black”) ice, which grows at the ice–water interface and has homogeneous crystal structure and a much smaller amount of impurities than sea ice or river ice (Kirillin et al., 2012). Hence, the heat balance at the IWI can be expressed as the sum of conductive (molecular) boundary fluxes and the heat release/consumption due to the phase change (freezing or melting) (Aslamov et al., 2014a):
where the vertical coordinate is directed downwards with the origin zi at the IWI; dhidt−1 is the rate of basal ice melting (growth); ρiLf is the product of the ice density and latent heat of fusion; Qiw is the conductive heat flux from/to the water,
and Qci is the conductive heat flux from/to the ice,
Temperature at the IWI is fixed at the melting point of 0 ∘C, corresponding to the following thermodynamic characteristics: the molecular heat diffusion coefficient for freshwater m2 s−1, the molecular heat diffusion coefficient for ice m2 s−1, the product of the water heat capacity and density is , and the same product for ice is (see, e.g., Leppäranta, 1983).
Equation (1) can be applied for reliable estimation of the ice–water heat flux Qwi if the temperature profile within the ice cover and the time variations of the ice thickness d hi d t−1 are known. This approach was used for estimation of the heat fluxes in Lake Baikal by Aslamov et al. (2014a), who recorded the temperature profile within the ice cover and the variations of the ice thickness dhidt−1 with high temporal resolution.
However, direct estimation of Qiw in the absence of detailed data on the ice cover dynamics and temperature is less straightforward. The bulk of the water column under the ice is turbulent: while ice-covered waters are isolated from the direct influence of wind, vertical heat transport remains higher than the purely molecular one, intensified by convective mixing due to solar radiation penetrating the ice cover and due to shear turbulence produced by under-ice currents. As a result, the thickness of the “diffusive” layer in the immediate vicinity of the ice base, where Eq. (2) holds true, does not typically exceed several millimeters. The temperature gradient dTdz−1 at z=0 is barely detectable by the traditional observation methods and varies continuously depending on the mixing and temperature conditions in the underlying water column.
The TKE under ice is supplied by the free convection in the underlying convectively mixed layer (Mironov et al., 2002) and/or by the mean horizontal current (McPhee, 1992; Aslamov et al., 2014a). In the latter case, the vertical turbulent transport of momentum is created by the current velocity shear at the ice base. Hence, close to the IWI, the distance from the ice base z is a major parameter, determining the turbulent mixing characteristics. Assumption of the proportionality between the mixing length scale and the distance from the solid boundary leads to the relationships for the neutral (logarithmic) boundary layer,
where z is the turbulent pulsation length scale equal to the distance from the lower boundary of the ice, z0 is the roughness length at the ice bottom, κ≈0.4 is the empirically determined von Kármán constant, and is the turbulent stress (shear velocity squared) produced by the vertical shear of the mean velocity S.
The logarithmic velocity distribution in the ice cover vicinity makes possible estimation of the momentum flux based on mean velocity values only using a direct relationship derived from Eq. (5) (“bulk” formula),
where the bulk transfer or drag coefficient CZ corresponds to the depth Z of the current speed measurements and is defined as
For a non-stratified steady-state turbulent boundary layer, the TKE budget tends to be the local balance of the largest terms in the TKE transport equation, production and dissipation:
where ε is the TKE dissipation rate.
The second factor influencing the buoyancy flux at the IWI is the destabilizing buoyancy flux BR due to volumetric absorption of solar radiation I(z) within the convectively mixed water column of thickness hS. The buoyancy flux is derived from the heat transport equation with the radiation term
Here, the assumption of a height-constant warming rate within the convective layer was used (Mironov et al., 2002). β=gαT(T) is the buoyancy parameter; αT is the thermal expansion coefficient. The latter is generally not constant in freshwater due to non-linearity of the equation of state at temperatures close to the maximum density value Tmd≈3.98 ∘C ( K−1; see, e.g., Farmer and Carmack, 1981).
The ice–water boundary layer in freshwater lakes is rarely neutrally stratified: a distinctive feature of the layer is the fixed temperature at the IWI. As a result, the water adjacent to the IWI in fresh or brackish environments is always subject to stable stratification, with deeper waters being warmer and thereby heavier. Stratification may alter the turbulent length scale, affecting Eqs. (4)–(7). Stratification counteracts the shear production of turbulence and in the asymptotic case of a strongly stratified layer is the sole mechanism of turbulence damping. This effect can be accounted for by introducing an additional length scale apart from the distance to the boundary z, as expressed by a simple formula following from dimensional analysis,
where Lx is the stratification length scale and Cx is an empirical coefficient. Equation (9) replaces Eq. (4) in stratified conditions with corresponding changes in Eqs. (5)–(7). For conditions dominated by the stabilizing buoyancy flux at the boundary , the stratification length scale turns to the well-known Monin–Obukhov length scale , with the empirically determined coefficient Cx≈5 (Stull, 2012), building the basis for the Monin–Obukhov similarity theory (MOST).
If stratification is created outside the boundary layer, its effect on boundary mixing is independent on the surface buoyancy flux. A characteristic length scale for turbulence in stratified media was independently proposed by Dougherty (1961) and Ozmidov (1965) as
where
is the buoyancy frequency and ρ is water density under the assumption of negligible salinity effects. Replacement of Lx by LN in Eq. (9) yields in this case
with the corresponding expression for the TKE production rate P being (cf. Eq. 7)
Close to the boundary, z≪LN, Eq. (11) approaches the neutral scaling relationship 4. At large distances from the boundary, z≫LN, Eq. (11) turns to a “z-less” scaling
which in turn yields the N scaling for P
In stably stratified conditions, production of TKE is counteracted by two major loss processes, dissipation ε and work against the stability forces BSt. The latter can be expressed in the form BSt=KρN2, where Kρ is the diapycnal diffusivity. From analysis of dimensions, the turbulent diffusivity can be scaled as (see, e.g., Monin and Ozmidov, 1981). Then, the TKE budget can be approximated as
with coefficients CN and CB subject to estimation from empirical data, or
where Ri is the gradient Richardson number,
expressing the relative importance of stratification and velocity shear for the vertical transport. Its critical value, (Turner, 1979), marks the boundary between turbulent conditions, at which the shear can destroy the stratification, and quiet conditions, at which strong N ultimately suppresses any turbulent motions. Hence, for turbulence to exist at weakly supercritical Ri, is required in Eq. (15). In the following we tentatively assume CB≈1. Another scaling relationship relevant to the turbulent mixing on the background of stable stratification is the buoyancy Reynolds number,
where m2 s−1 is the water viscosity. Reb refers to the work of turbulence against stratification and viscosity, which becomes important at distances from the solid boundary shorter than characteristic length scales of turbulence; its critical value is reported to be 𝒪(101) (Gargett et al., 1984).
In neutral conditions, the coefficient of turbulent heat transfer (assuming the turbulent Prandtl number is approximately 1), and the corresponding relationship for the ice–water heat flux Qiw (Eq. 2) can be written as
where ΔT is the temperature difference across the layer hT beneath the ice base, often assumed in models as water temperature at the vertical grid point closest to the ice. The expression is sometimes used in the form of the bulk formulation, assuming direct relationship between the friction velocity and the main current speed (cf. Eq. 6):
where ΔT is the temperature difference across hT, and CQ is an empirical bulk heat transfer coefficient. The values of CQ were reported in the range (Hamblin and Carmack, 1990; Nan et al., 2016); stratification effects on CQ were not investigated.
When the same scaling considerations are adopted as in Eqs. (14)–(15), the heat flux at the IWI Qiw in strongly stratified conditions may be assumed to depend on the work of turbulence against the stability,
or, in terms of buoyancy flux Biw,
Herewith, a strongly stratified case is characterized by the flux dependence on the shear velocity squared and a weaker dependence on the stratification, expressed by the exponent 1∕2 at the vertical density gradient (as revealed by the direct proportionality to the buoyancy frequency N).
Summarizing the considerations above, validation of the Dougherty–Ozmidov (D–O) scaling (Eqs. 10–14) for the ice boundary layer and the ice–water flux parameterization (Eqs. 18–20) is possible when field data are available on both the TKE dissipation rates and the mean fields of governing forces (production of convective instability by radiative heating and/or mean horizontal flow due to under-ice currents).
The field study was performed in February–March 2017 in the southern part of Lake Baikal. Two custom-made autonomous stations were installed in the vicinity of a quasi-stationary alongshore current (Fig. 1). Under-ice currents with characteristic velocity and spatial scales of 10−2– and 104–105 m, respectively, have been regularly observed in this region during the ice cover period (Aslamov et al., 2014a, 2017). The scales of the flow suggest that away from boundaries it is balanced mainly by the Coriolis force, while the forcing may be attributed to density gradients created by in- and outflows, and topographic effects.
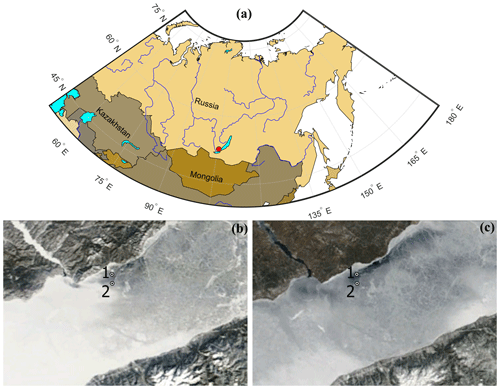
Figure 1(a) Geographical location of the study site. Ice conditions in the southern part of Lake Baikal on (b) 9 February and (c) 12 April 2017 and locations of the autonomous measurement stations. The satellite images are from the Irkutsk Center of Remote Sensing (sputnik.irk.ru, 2019). Note the stronger ice melt in the area of the jet current around station S1, visible as a dark area in (c).
Station S1 was installed 4.5 km away from the lake shore (51∘51.923′ N, 105∘4.779′ E) in the area of quasi-stationary jet-like alongshore current. Station S2 was located 3.5 km to the south of station S1. The total water depth in the vicinity of both stations amounted to ≈1400 m. Each station registered temperature at 30 vertical levels distributed within the ice cover, the water boundary layer, and the air above the ice. The distance between temperature sensors was 5 cm within the ice and in the under-ice boundary layer, increasing up to 10–50 cm at larger distances from the ice boundary in the water and in the air. Three short-wave solar radiation sensors were deployed vertically to measure the decay of solar radiative fluxes across the air–ice–water system. Ice thickness was measured by a 330 kHz echo sounder, deployed upward-looking at a fixed distance from the ice surface. The resolution of the system was 0.002 ∘C for temperature, 0.1 W m−2 for solar radiation, and 0.1 mm for ice thickness (operational range of 0.2–2.8 m). The system collected data for a period of 2 min, logged them internally, and sent data several times a day via a cellular network to a remote Internet server (see Aslamov et al., 2017, for a detailed description of the ice station configuration). Two-dimensional electromagnetic current meters, “INFINITY-EM” (JFE Advantech Co., Ltd.), were used to measure the current velocities (velocity range: ; resolution: 0.02 cm s−1; accuracy: ). The current meters were positioned at a distance of 1 m from the surface of the ice cover. Three additional current meters were deployed at station S1 at distances of 0.6, 0.8, and 1.4 m from the ice surface.
Characteristics of turbulent mixing in the under-ice boundary layer were obtained with the help of the high-resolution Doppler current velocity profiler HR-Aquadopp (Nortek AS, Norway). The profiler was deployed for 48 h successively at each of the two stations, on 5–7 March 2017 at station S1 and on 8–10 March at station S2. The profiler was frozen into the ice facing downward, with the acoustic head 2 cm beneath the ice base (verified with a remotely operated vehicle (ROV) camera). Three components of current velocity were registered with a time interval of 2 s and a spatial resolution of 15 mm in the pulse-to-pulse coherence (high-resolution) mode.
The values of short-period fluctuations of the flow velocity were used to calculate dissipation rates of TKE based on Kolmogorov's 1941 hypothesis on the self-similarity of the velocity structure functions using the method described by Wiles et al. (2006). ε was derived as a coefficient in the semi-empirical equation for the velocity structure function Di(r) along the ith acoustic beam,
which includes noise estimation (Noise) due to instrumental noise and non-turbulent velocity fluctuations. Here, the constant (see, e.g., Lien and D'Asaro, 2002). The velocity structure function was calculated from the measured along-beam velocities vi(z) at the distance z from the instrument's head as
A quality check was performed based on values of Noise in Eq. (21); the ε values from three beams were compared for similarity and averaged. The detailed procedure of data post-processing and the quality check is described by Kirillin et al. (2018) and Volkov et al. (2019).
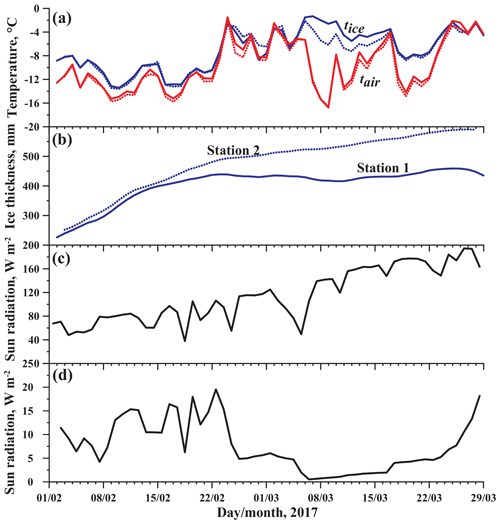
Figure 2Background data on the Lake Baikal ice regime during the observations: (a) daily averaged temperatures of ice surface (tice) and air temperatures at 1.5 m above the ice (tair), (b) ice thickness, (c) incoming solar radiation, and (d) penetrated solar radiation. In (a) and (b) solid lines correspond to station S1 and dotted lines are for station S2.
4.1 Atmospheric conditions and ice cover thickness
The ice cover formed on Lake Baikal during the second half of January 2017, with several periods of ice break-up and re-freeze. The autonomous stations were installed on 1 February 2017 and provided background information on the major forces driving the ice cover development. The temperatures of the ice surface remained below the freezing point of water during the entire observation period, varying between −14 and −2 ∘C with a slight warming trend (Fig. 2a). The initial ice thicknesses were nearly the same at both stations: 23 cm at station S1 and 24 cm (a day later) at station S2. During the first 2 weeks of February the ice grew at a nearly constant rate of 1.2–1.3 cm d−1 (Fig. 2b). During this period, the ice surface temperatures at both stations were nearly equal and followed closely the air temperatures at a height of 1.5 m. This quasi-neutral stratification in the air–ice boundary layer lasted until the end of February, caused apparently by convective heat flux from the ice surface due to release of the latent heat of ice formation. Later, the ice thickness at station S1 (the one with strong under-ice currents) remained nearly constant, while basal ice at station S2 continued to grow at a slow rate of ≈0.3 cm d−1 (Fig. 2b). In mid-March, a stable stratification developed in the air above the ice, with air temperatures dropping down to −16 ∘C. Whereas the temperature at the ice surface of station S2 also decreased following the air temperature trend, the ice surface at station S1 remained relatively warm, suggesting, together with the nearly constant ice thickness, a balance between the heat release to the atmosphere and the heat supply from the water column.
4.2 Mean currents, temperatures, and stratification
The thermal structure was similar at both stations S1 and S2 (Fig. 3): under ice, the water temperatures slightly increased with depth. The mean vertical gradient of 0.6 ∘C over the upper 10 m of the water column was about an order of magnitude weaker than those typically observed in shallow ice-covered lakes (Kirillin et al., 2018). Below 10 m depth the water column was well mixed vertically down to 30 m. Closer to the ice base, two horizontal layers could be distinguished: a <0.5 m thin layer adjacent to the ice with a temperature difference of ≈0.3 ∘C across it. Underneath, a layer with nearly linear temperature increase of ≈0.03 spread down to 10 m depth.
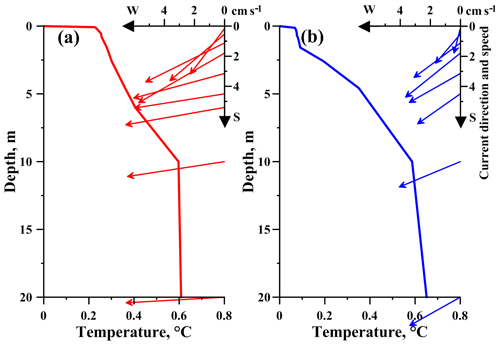
Figure 3Temperature and current velocity vector profiles measured from 14:00 to 16:00 LT (local time) on 6 March 2017 at (a) station S1 and (b) station S2.
In terms of stability, the two-layered thermal structure can be described by two nearly constant buoyancy frequencies: in the layer and in the layer , where the thickness of the sub-ice layer δ≈0.4 m and the lower boundary of the stratified IL hS≈10 m.
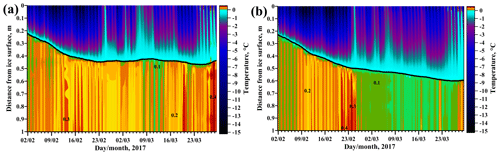
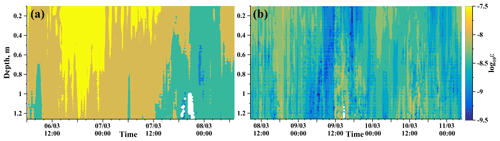
Figure 4Temperature maps in the ice boundary layer and within the ice cover at station S1 (a) and station S2 (b). Note the different color scales for ice and water.

Figure 5Horizontal current speeds at station S1 (a, c) and station S2 (b, d) measured by the acoustic Doppler profiler Aquadopp (a, b) and the electromagnetic loggers INFINITY (c). (a)–(c) are the time–depth maps; (d) shows the horizontal flow speed measured by a single INFINITY logger at 1 m under ice (thin red line) and the Aquadopp velocity record from the same depth (thick blue line).
The two-layer structure was less distinct and the mixed-layer temperature was slightly higher at S2 (Fig. 3b); S1 had in turn a stronger vertical gradient close to the ice base. These temperature differences between the two stations suggested a stronger upward heat transport at S1 due to stronger vertical mixing caused by water flow. Current speeds were indeed almost twice as high at S1 than at S2 (Figs. 3 and 5). The currents in the upper 20 m of the water column had a uniform WSW direction aligned with the shoreline (see velocity vectors in Fig. 3). A weak, 10–15∘ anticlockwise rotation of the current vector was detectable within the 1–2 m thin layer adjacent to the ice base, suggesting some effect of the Coriolis force on the boundary layer currents.
The diurnal and synoptic variations of the ice and water temperatures were similar to those observed in the previous years (Aslamov et al., 2014a, 2017). The diurnal temperature oscillations driven by the solar radiation cycle were apparent in both water column and ice cover, with amplitudes decaying towards the ice–water interface. The beginning of the melt phase after 26 March 2017 was indicated by homogenization of the ice cover temperature at the melting point of 0 ∘C. Earlier, occasional increases of the air temperature, for instance on 25 February, provoked deceleration of the ice growth or short-term melting periods at both stations (Fig. 4). Relevant to the matter of the present study, a remarkable increase of the ice temperatures was observed at both stations during the period of turbulence measurements on 6–12 March. The warming was not correlated with the air temperature: the latter dropped significantly during the same time (Fig. 2). At S1, the warming was strong enough to produce a decrease of the ice thickness (Fig. 4a), while the effect at S2 was too weak to cause any ice melt (Fig. 4b).
The mean currents obtained with the acoustic Doppler profiler at a time interval of 2 s and a spatial resolution of 15 mm (Fig. 5a and b) agreed remarkably well with the records from the five electromagnetic velocity loggers at coarser temporal and spatial resolution (Fig. 5a and b). The result allowed later extension of the boundary layer turbulence analysis to the whole period of electromagnetic velocity measurements, after a relationship between the mean flow characteristics and the turbulent energy production was established from the short-term acoustic profiling.
The mean current velocities from the two neighboring stations demonstrated different water flow patterns. At station S1, current velocities in the upper 1 m of the water column had mean values m s−1. The magnitudes underwent variations on synoptic timescales, changing at 1 m under the ice from to m s−1 within 48 h (Fig. 5a). The event coincided with melting of the ice cover (Fig. 4a), suggesting that the upward heat transport by the currents is the mechanism of ice heating in this case despite the low air temperatures (Fig. 2a). Farther from the lake shore, at station S2, the currents, as measured during the next 2 d, revealed lower variability with time and had lower magnitudes of 1 to m s−1.
4.3 Solar radiation
The solar radiation flux at the ice surface doubled within the 2 months of observations (Fig. 2c), contributing to the deceleration of the ice growth. The light conditions under ice were estimated from continuous measurements of photosynthetically active radiation (PAR) I(z) at the single depth z=1.5 m under the ice surface assuming one-band exponential decay of radiation flux (Beer's law) . We estimated the decay rate of radiation within the water column (light attenuation coefficient) γ using PAR profiles collected in previous studies in 2011, using the evidence that year-to-year variations of water transparency of Lake Baikal are small (Hampton et al., 2008). The light attenuation coefficient was estimated from nine PAR profiles as . The radiation flux at the ice bottom amounted to ≈1–18 % of the surface radiation and varied depending on the snow conditions at the ice surface (Fig. 2d). The mean daily under-ice short-wave radiation was I0=9.7 W m−2 with maximum values of up to 23.5 W m−2. The drop of the under-ice solar radiation after 23 February (Fig. 2d) was caused by a (relatively light, <0.5 cm) snowfall, which prevented light penetration through the otherwise transparent congelation ice. Variations in the under-ice radiation could have affected the temperature distribution under ice by slowing down or even canceling the warming in the convectively mixed layer at depths below 10 m.
With γ and I0 known, we estimated the theoretical thickness of the stratified interfacial layer δR. For a single-band exponential decay of the short-wave solar radiation within the water column , the steady-state solution of the radiation–conduction balance in a layer of thickness δR can be written as (Barnes and Hobbie, 1960)
which represents a transcendental equation with respect to δR. When substituted in Eq. (23), the values of I0 and γ yield δR≈0.2–0.4 m, adopting the temperature of the well-mixed layer of 0.6 ∘C for Tm. The estimate coincides well with the observed thickness of the ice-adjacent gradient layer δ (Fig. 3). The non-zero vertical temperature gradient beneath this layer is in contrast to the typical picture of convection in ice-covered lakes and suggests that the part of the convectively mixed layer is altered by the turbulent shear due to under-ice currents. Based on this suggestion, the under-ice radiation values were used to estimate the destabilizing buoyancy flux from Eq. (8) across the linearly stratified layer as . The resulting estimations are IR≈2 W m−2 and . The characteristic scale of convective velocities (Deardorff, 1970) , which agrees well with previous reports on radiative convection under lake ice (Mironov et al., 2002; Kirillin et al., 2018; Volkov et al., 2019). These estimates of the convective velocities suggest that radiation was of minor importance for the mixing conditions in the boundary layer compared with the mean flow (cf. Fig. 5), especially after 23 February, when the subsurface radiation level dropped significantly. Therefore, shear and stratification in the boundary layer appeared to be the major factors determining water–ice heat transport.
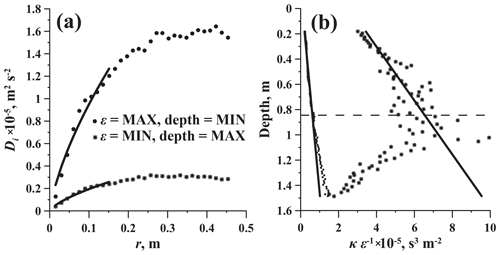
Figure 6Turbulence-related characteristics of the boundary layer: (a) velocity structure functions for high (circles) and low (asterisks) levels of TKE dissipation rates. Solid lines are the approximations by Eq. (22). (b) Vertical profiles of the reciprocal TKE dissipation rates κε−1 for conditions of high (circles) and low (asterisks) turbulence. Solid lines are the data approximations by Eq. (7). Horizontal dashed line in (b) marks the depth equal to the mean Ozmidov length LN≈0.8 m
4.4 Turbulence intensities in the ice–water boundary layer
Fluctuations of current velocities around their means were characteristic of developed turbulence: the structure functions (Eq. 22) scaled well as the distance to the power of 2∕3 clearly demonstrating the existence of the inertial interval in the wavenumber domain (Fig. 6a). According to the 2∕3 power scaling, the upper boundary of the inertial interval reached 0.1–0.3 m, which can be treated as a characteristic size of turbulent eddies. In low-turbulence conditions , the TKE dissipation rates were at their minimum at the depth of ≈0.8 m and increased towards the ice base (asterisks in Fig. 6b), supporting the scaling (Eq. 7). The scatter of ε around the straight line increased with the distance from the ice z, starting from z≈Le. During periods of high turbulence (), the reciprocal of the TKE dissipation rate ε−1 increased with depth more homogeneously. Nevertheless, a small local extreme in the line ε−1(z) and a slight change of the slope were recognizable at the same critical distance from the ice (circles in Fig. 6b).
In the area with weak under-ice currents at S2, the TKE dissipation rates ε varied around a value of , close to the threshold between turbulent and laminar conditions. In turn, the average ε in the vicinity of the jet-like under-ice current at S1 was 2 orders of magnitude higher (Fig. 7). In contrast to the under-ice water temperatures, neither TKE dissipation rates nor friction velocities demonstrated any diurnal variations, suggesting a minor effect of the radiation-driven convection on turbulence generation. Instead, an apparent correlation existed between the turbulence intensity ε and the temporal variations of the mean flow velocities (Fig. 7): the highest TKE dissipation rates of were observed during current intensification up to 𝒪(10−1) m s−1 at S1.
The maximum values of the D–O length scale (Eq. 10), averaged over the period of observations, decreased with the distance from the boundary from LN≈1.5 m at z≈0.2 m to LN≈0.9 m at z≈0.9 m. The decrease in LN followed the decrease of ε. Here, the mean NS in the layer with quasi-linear stratification of 0.5–10 m beneath the ice base was used as a characteristic value of the buoyancy frequency in the D–O scaling. At larger distances from the ice base, LN remained nearly constant, varying between 0.8 and 0.9 m. Hence, the value can be treated as a boundary between the “quasi-neutral” and strongly stratified z-less layers, with the turbulent length scale defined by the distance z closer to the ice base, and by LN at farther distances.
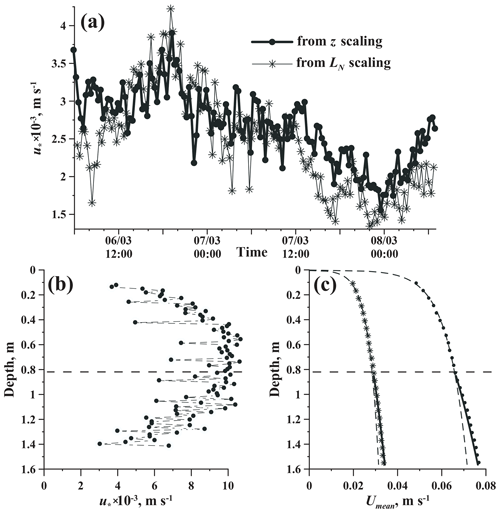
Figure 8Ice boundary layer structure: (a) friction velocity u* at station S1 as determined from the quasi-neutral production–dissipation balance (Eq. 7, thick solid line with symbols) and from the Dougherty–Ozmidov length scale (Eq. 13, thin lines) at a distance from the ice base nearly equal to the mean Ozmidov length LN≈0.8 m, (b) mean vertical profiles of u*, and (c) vertical velocity profiles for strong (circles) and weak (asterisks) currents. The two profiles in (c) correspond to those in Fig. 6. Horizontal dashed line in (b, c) marks the depth equal to the mean Ozmidov length LN≈0.8 m
An important insight into the mechanisms of turbulence generation under ice is provided by comparison of the stratification-based turbulence scaling (Eqs. 10–13) against the quasi-neutral law-of-the-wall (LOW) relationship (Eqs. 5–7). At z<zcrit, both “neutral” relationships (Eqs. 4 and 7) produced similar estimations of the friction velocities u* with 20–30 % higher values produced by u* estimations from ε (Eq. 7). While the value of the von Kármán constant in the neutral LOW scaling κ≈0.4 is relatively well known from tunnel experiments and numerical simulations, and it is supported by field data, the proportionality constant in Eq. (13) is not well established. Therefore, for z-less D–O scaling (Eq. 13), the values of u* were calculated from Eq. (13) assuming a unity coefficient of proportionality CN. On average, the “stratified” scaling produced generally lower values of u* at farther distances from the ice bottom and vice versa. The D–O scaling with CN=1 and LOW demonstrated nearly perfect agreement at (Fig. 8a). This fact justified the balance between the shear production at the boundary and the stratified production of turbulence at this distance from the wall, as well as supporting the choice of the unity constant in the D–O scaling. Accordingly, CN=1 was adopted for later application of the combined log-linear scaling (Eqs. 12 and 14).
The combined log-linear scaling (Eq. 12) with CN=1 produced u* close to the neutral value in the vicinity of zcrit and decreased towards both IWI and the open water column (Fig. 8b). Like the TKE dissipation rates, the mean current speeds demonstrated behavior characteristic of the stationary boundary layer, i.e., fitted well to logarithmic profiles at distances from the IWI less than zcrit (Fig. 8c). Farther from the ice base the mean velocity profiles were nearly linear, with the slope close to .
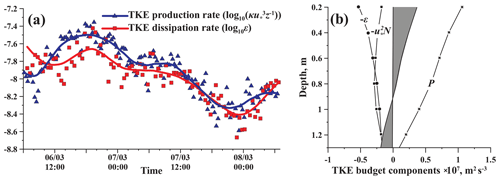
Figure 9TKE production–dissipation balance in the ice boundary layer. (a) TKE production and dissipation rates at the depth of 0.85 m beneath the ice base. Bold lines are the values filtered by a moving average with a 6 h window. (b) Vertical profiles of the TKE budget components in Eq. (14) averaged over the 2 d period of measurements. Data are presented for station S1 only; the S2 results are qualitatively the same.
The integral balance between the TKE loss terms and the turbulent energy production (Eq. 7) held true within the 1.5 m thick layer covered by measurements of ε: the mean difference between the two terms integrated over the entire layer did not exceed 0.2 %; temporal variations of the dissipation rate followed closely those of the shear velocity (Fig. 9a). The balance was disturbed only at current speeds <0.02 m s−1, with a corresponding drop of ε down to at station S2 on 9 March 2017 (not shown). During this same period, the vertical flow profiles showed a significant deviation from the logarithmic form, indicating laminarization of the boundary layer under these conditions. The boundary value of the friction velocity for the transition to a turbulent regime was m s−1. The mean balance between the production loss terms in Eq. (14) varied, however, with the distance from the ice base (Fig. 9b): close to the ice–water interface the production significantly exceeded dissipation, while below the depth of ≈0.8 m the dissipation prevailed above the production. Remarkably, this transition depth agreed well with the thickness of the layer where .
The good agreement of the measured velocity profiles with the logarithmic approximation at z<zcrit allowed estimation of the roughness of the ice bottom surface z0 from Eq. (5). The mean z0 amounted to 1.00 mm with a maximum of 3.5 mm and minimum of 0.2 mm. The roughness had a significant (Pearson's coefficient of −0.52, p≪0.01) negative correlation with the mean velocity as .
Our estimations of z0 and u* yielded the following parameters for the bulk formula Eq. (6): and , where C1 m is the bulk transfer coefficient for the momentum flux at 1 m depth. The independent measurements of current velocities at four depths made by the single-point 2-D horizontal current loggers INFINITY demonstrated good agreement with Eq. (6) when scaled against u* from the HR-Aquadopp measurements (Fig. 10).
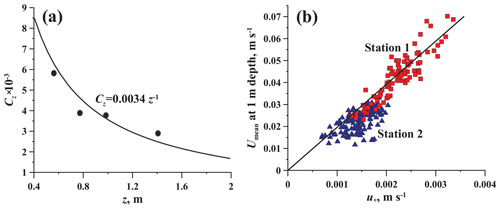
Figure 10Bulk characteristics of the ice boundary layer: (a) bulk transfer coefficient for momentum CZ as a function of distance from the IWI, where dots are values calculated using the horizontal velocity data from point measurements by 2-D INFINITY-EM loggers, and the line is an analytical approximation; (b) relationship between the mean flow velocity at z=1 m and the turbulent stress.
The simple result has large potential for application in modeling of the ice–water boundary layer at strong under-ice currents with a minimum of input information; care should be taken, however, regarding the thickness of the nearly logarithmic layer and its dependence on the under-ice stratification – the effect described above and discussed in more details below.
4.5 Heat budget at the ice base and relation of ice–water heat flux to under-ice mixing
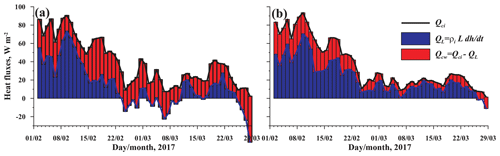
The heat balance at the IWI was calculated by Eqs. (1) and (3) using data on temperature within the ice cover and ice thickness variability measured by the echo sounder. The ice–water heat flux was generally stronger at station S1, correlated with stronger currents and mixing intensities. Already at the beginning of the observation period in February, the upward conductive heat loss Qci of up to 80 W m−2 was compensated to 30–50 % by the heat supply from the water column Qiw. The latter significantly reduced the ice growth rate and latent heat release (cf. red and blue areas in Fig. 11).
During 24 February–7 March the snow cover reduced the heat release to the atmosphere, which also lowered the conductive flux at the ice base Qci (Fig. 11). As a result, the heat flux from water to the ice at S1 (Fig. 11a) exceeded that from the ice to the atmosphere, producing melting at the ice base (negative QL) despite continuing surface cooling (Qci remained positive with values of up to 40 W m−2). After 25 March, ice cover started to melt at both stations, coinciding with an increase of air temperatures above the freezing point (Fig. 2). Quantitatively, the ice–water heat fluxes at S2 were in the range of 5–10 W m−2, which agrees with estimations from earlier lake studies. However, Qiw at S1 had appreciably higher values, reaching up to 40 W m−2 at their peaks.
An attempt to link the ice–water heat flux with the mixing characteristics in the stratified boundary layer in the form of a bulk relationship (Eq. 19) provided a remarkable result: the heat flux at the IWI and the dissipation rate of the TKE are linked linearly (Fig. 12a), or in terms of buoyancy flux B:
Here, ε is taken at the distance zcrit=0.85 m from the ice base, which corresponds to the boundary between the ice-adjacent sublayer and the linearly stratified boundary layer (see Sect. 4.2).
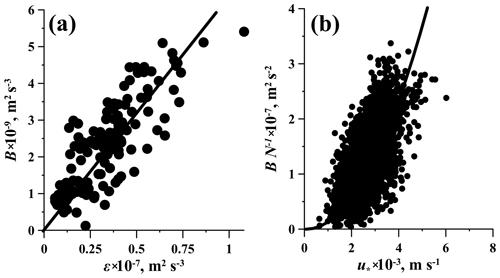
Figure 12Buoyancy flux at the ice–water interface B as a function of (a) TKE dissipation rate ε and (b) friction velocity u*.
The linear correlation between the ice–water heat flux and ε supports the scaling (Eq. 20) in the stratified boundary layer under ice: from the two bulk relationships Eqs. (18) and (20), the former suggests and the latter agrees with the observed linear dependence Qiw∝ε. Herewith, the result discards the widely used bulk relationship and suggests that Qiw scales as friction velocity squared (Eq. 20) or, in terms of Eq. (19), . The dependence is well supported by our data, though the scaling is less apparent at very low u* due to the lack of values at low turbulence levels. Still, the data on Qiw(u*) (Fig. 12b) clearly demonstrate the inappropriateness of the quasi-neutral scaling (Eq. 18). Instead, the flux can be parameterized as
where NS is the quasi-constant buoyancy frequency in the boundary layer .
Our study presents the first detailed assessment of mixing conditions under the ice cover of Lake Baikal and their effect on the growth and melt of the ice cover. The seasonal ice cover is Lake Baikal's inherent feature, whose role in the functioning of this unique ecosystem remains not fully understood. In this regard, the outcomes of the study underscore the importance of the lake-wide circulation for the ice cover duration and ice thickness. The applicability of the results extends, however, beyond Baikal-specific conditions. Lake Baikal shares the major features of seasonal ice cover with other lakes, as well as with inland and marginal seas, allowing extension of the results to other ice-covered waters. Furthermore, the ice–water boundary layer in Lake Baikal possesses a remarkable feature relevant to fundamental problems of environmental fluid mechanics: a strong boundary-layer flow in the background of permanent stable density stratification. In our study we successfully tested an alternative approach to the traditional Monin–Obukhov similarity theory, based on the Dougherty–Ozmidov scaling. We also revealed several important facets of the turbulent energy budget in stratified boundary layers and established a relationship between the shear turbulence under ice and the heat flux at the ice–water boundary.
The high values of water–ice heat fluxes in Lake Baikal and their apparent relationship to the intensity of under-ice currents were previously noted by Aslamov et al. (2014a, 2017). In the present study, the measured fluxes reached up to 40 W m−2 at their peaks, which is an order of magnitude higher than values reported from small Arctic lakes (Kirillin et al., 2018) and comparable to the highest reported values in alpine thermokarst ponds (Huang et al., 2019) and in the ocean (Gallaher et al., 2016; Peterson et al., 2017). Concurrent registration of fluxes, current velocities, and dissipation rates of the TKE reveals the direct link between turbulence production by the velocity shear and ice growth (ablation). The finding contradicts the conventional assumption on the major role of convection produced by the solar radiation penetrating the ice in under-ice mixing of freshwater lakes. While radiatively driven convection is a prominent feature of freshwater lakes (Farmer, 1975; Yang et al., 2017; Volkov et al., 2019) and effectively mixes the upper water column of Lake Baikal in winter (Granin et al., 2000; Jewson et al., 2009), its effect on the boundary mixing and heat transport to the ice base appears to be restricted by the stable stratification in the relatively thin interfacial layer, with water temperature increasing from the melting point at the IWI to that of the convectively mixed layer (Kirillin et al., 2018). As a result, the energy of convection partially dissipates within the convective layer and is partially spent for entrainment of deeper waters at the base of the mixed layer (Mironov et al., 2002). The rate of the energy dissipation produced by convection in small lakes (Volkov et al., 2019) is about 10−9–10−8 W kg−1, which is roughly an order of magnitude lower than that measured in this study. Consequently, the turbulence budget in the boundary layer differs significantly from that reported in previous lake studies. The TKE production averaged over the entire observation period prevails over dissipation at z<LN, while in the deeper part of the boundary layer ε slightly exceeds the production. Herewith, the boundary mixing continuously pumps turbulent energy downwards, contributing to destruction of stratification in the main SL . The opposing trend is created by solar radiation, which increases the temperature of the convectively mixed layer Tm and thereby creates an upward exponential decrease of temperature from Tm to the freezing point Tf. The observed quasi-linear stratification in the SL is apparently a result of the two opposing forces leading to a nearly steady-state conditions characterized by a constant N within the layer .
A particular advance in estimation of the turbulent energy budget under ice was achieved by direct estimation of the TKE dissipation rate using the velocity structure method. By doing so, we (i) avoided applying Taylor's “frozen turbulence” hypothesis, which remains questionable at relatively low current velocities under ice, and (ii) were able to trace the vertical distribution of ε across the boundary layer (at least a part of it, covering ∼2 m). On the one hand, this extended information allows better quantification of the turbulent structure; on the other hand, it poses some fundamental questions about the major forces behind under-ice mixing and heat transport, to be discussed below.
Close to the ice base, vertical profiles of the TKE dissipation rates decayed as , supporting the scaling of the turbulent mixing length with the distance from the solid boundary, similar to neutral or nearly neutral conditions. This fact gives a solid background to estimation of the shear velocity u* from the mean velocity profiles: the latter method is often uncertain, given that neither depth of the logarithmic layer nor ice roughness are known a priori. However, the thickness of the layer with varies depending on the current speed and mixing intensity. At strong currents, dissipation followed the scaling across the entire depth of the high-resolution velocity measurements of 1.4 m; at , it reduced to several tens of centimeters. The maximum mixing length scales remarkably well against the Dougherty–Ozmidov length scale: using NS as the characteristic value for stratification, LN=1.2 m at W kg−1 and LN=0.4 m at W kg−1. Qualitatively the result can be treated as follows: the shear at the ice base dominates in the turbulence production at distances from the ice base less than LN, while farther from the source of the shear the stratification limits the size of the turbulent eddies. This structure is also supported by comparison of the friction velocities computed from the two mixing lengths, Eqs. (7) and (13): u* tends to be overestimated by the Ozmidov scaling at high mixing rates close to the ice base, and it becomes lower than that produced by z scaling at larger distances from the ice. At z≈LN both estimations provide equal results (see Fig. 8). In the TKE budget, the depth z>LN is also a turning point, where Eq. (14) shows a close balance between turbulence production and damping.
Generally, the simplified model of the TKE balance Eq. (14) was well supported by the data. The discrepancies included the prevalence of TKE production over the damping terms closer to the ice cover and a slightly lower TKE production rate than the sum of the lost terms at z>LN. The imbalance can be tentatively attributed to downward advection of the TKE. Furthermore, the balance was estimated under the assumption of constant buoyancy frequency N, neglecting a possibly stronger loss of the TKE closer to the ice, where N increases. We also neglected possible transport of turbulent energy produced by convection due to solar heating. The latter can, however, be assumed to be small: within the stratified layer, the radiation levels under ice produced a destabilizing buoyancy flux of only 𝒪(10−10) W kg−1, and the convectively mixed layer was located several meters beneath the deepest point covered by measurements.
The proposed scaling of the TKE budget differs from the conventional MOST approach by using the Dougherty–Ozmidov length scale instead of the Obukhov length scale, i.e., by replacing the surface buoyancy flux with the mean stratification as a major scaling variable. This alternative approach is convenient for analysis of observational data: in contrast to the surface fluxes, N is easily measurable in oceanic and lake studies. Noteworthily, these scaling approaches have been shown to be interchangeable (Grachev et al., 2015). In the particular case of ice-covered waters, the D–O approach is also more physically sound than MOST; since the surface buoyancy flux does not dominate the turbulent conditions under ice, it is rather a result of the upward heat transport from deeper waters. One of the derivatives of the D–O boundary layer scaling is the relationship , which also implies that the length scale can be used instead of LN without any basic changes in the model assumptions. This scaling was previously considered, for example, by Zilitinkevich and Mironov (1996) and is preferable for testing and refining the model parameters if observations of u* are available at high resolution.
The presence of an ice-adjacent interfacial sublayer is another remarkable feature of the shear-dominated ice boundary layer. The thickness of the layer (δ≈0.2 m) was close to the smallest estimate based on the solar radiation of the layer created between the fixed temperature at the ice base and a convectively mixed homogeneous layer beneath. Our temperature measurements were too scarce to trace the evolution of its thickness at variable current velocities. Some insight into the genesis of the layer can, however, be obtained by assuming the largest value of the Dougherty–Ozmidov length scale LN≈0.85 m as the maximal thickness of δ. In this case, the mean buoyancy frequency in the interfacial sublayer Nδ≈0.02 s−1. That leads to the buoyancy Reynolds number Reb≈16 and the gradient Richardson number Rig≈0.4. Both values are close to the critical values of 𝒪(101) and 0.25, respectively. The layer may therefore be assumed to stay in a near-critical turbulence-free state. In the rest of the boundary layer, both Rig and Reb are far beyond the critical values, indicating developed turbulence.
The following structure can be tentatively drawn from the above analysis (Fig. 13): the background vertical temperature (density) distribution is formed by absorption of solar radiation and the upward heat flux to the ice, producing the profile typically observed in ice-covered lakes without strong currents: a nearly homogeneous convectively mixed layer with a relatively thin stratified layer on top. Mixing by the velocity shear reduces the density gradient. In the top layer, shear mixing is balanced by solar heating from above, so that the density gradient tends to the critical value between turbulent and non-turbulent states. In the upper part of the homogeneous layer, a weaker nearly linear density gradient forms. In the larger part of this layer, at z>LN, the turbulence production is balanced by the stratification, in accordance with z-less linear scaling, Eq. (13). Beneath the depth LN, the scaling suggests , which is also supported by the measured mean velocities (Fig. 8). The stratification is nearly linear, suggesting also that ε is nearly constant across it. The thickness of the layer depends apparently on the scales of the under-ice flow. The shape of the observed temperature profiles slightly deviates from linearity, with a tendency to re-stratification corresponding to weaker currents at S2 (Fig. 3b). Apparently, variations in the current speeds may affect the general tendency to linear stratification, producing changes in the heat content of the upper water column caused by horizontal advection of heat, or by re-stratification during periods of low shear. We do not possess enough well-resolved data on temperature to investigate these effects.
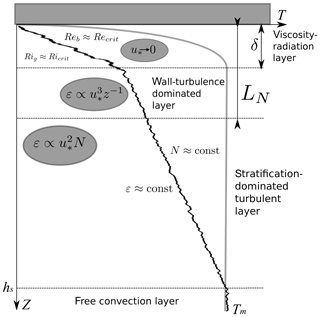
Figure 13Formation of the vertical temperature profile in a shear-driven ice boundary layer. Gray line is a no-shear original profile; black line is the result of shear-driven turbulence on the background of stable stratification. See text for notations.
We did not consider the rotational effects on the boundary layer characteristics. A slight Ekman-like rotation of the mean current was observed under ice (Fig. 3), and the Ekman scale based on the mean shear velocities is 𝒪(101) m. Herewith, the Coriolis force may have an effect on the thickness of the boundary layer. At weak stratification, effects of both N and f on the boundary layer dynamics may appear comparable, so that the model will perform better if the length scale LN (or its equivalent ) is replaced by the combined length scale . The latter scaling was proposed by Pollard et al. (1972). Zilitinkevich and Mironov (1996) suggested that the fN scaling has a rather limited area of application. However low flow velocities and weak stratification are typical for conditions under ice, and the Pollard et al. (1972) scaling may find its application in ice-covered waters. More data are required here, in particular, on the fine density and flow structure over the entire Ekman layer.
The main motivation of the study was seeking the relationship between the shear mixing and stratification on the one hand and the heat release from water to the ice cover on the other hand. In this regard, the scaling of the heat (buoyancy) flux with the shear velocity squared and the buoyancy frequency under ice (Eq. 20) is our major finding, with implications for a wide range of ice-related problems. The simple bulk approximation Eq. (19) is widely used in models of ice–water interaction, but its validity was never thoroughly tested before. The simple relationship , equivalent to Eq. (19), failed to describe the heat flux dynamics in the ice boundary layer, replaced by the scaling . The result suggests that the effect of the currents on the decrease of the Arctic sea ice may appear much stronger than assumed by the present model projections, based on the bulk estimation . Further decline of the Arctic ice cover may result in both increase of the under-ice current speeds due to changed global circulation and increase of the stratification due to warming of the under-ice waters. Both factors, according to our scaling will accelerate the vertical heat transport from water to ice, resulting in a positive feedback on the ice melt. Hence, incorporation of the under-ice density stratification in the heat flux parameterizations may significantly improve the outcomes of the oceanic ice models, especially for the ice melt periods, when freshening of the under-ice boundary layer produces strong salinity stratification.
In contrast to the surface heat flux, the bulk formulation Eq. (6) worked well for the momentum flux thanks to the nearly constant shear conditions close to the ice base. The result is of practical use in simple models of ice-covered seas and lakes, where u* can be directly approximated from the mean current speeds at a certain distance from the IWI (Fig. 10). The speeds should, however, be known at distances from the ice z<LN; otherwise, the stratification effects on turbulence production make the bulk formula unrepresentative.
We investigated the fine vertical structure of turbulence characteristics in the boundary layer of Lake Baikal and proposed a model of stratified turbulent ice boundary layer based on the Dougherty–Ozmidov length scale of turbulence. In contrast to small lakes, where solar radiation dominates ice–water heat exchange, the water–ice heat flux in Lake Baikal was strongly affected by the mean flow shear, similar to the ice boundary layer in the ocean. The shear-produced mixing was counteracted by the stable density stratification beneath the ice cover. Absolute values of the water–ice fluxes were an order of magnitude higher than those in no-shear conditions, ensuring basal ice melt even during cooling at the ice surface. The ultimate result consists in scaling of the water–ice heat flux against the shear velocity squared. The result suggests large errors in heat flux estimations when the traditional bulk approach is applied to stratified conditions with strong shear. It also implies that under-ice currents may have a much stronger effect on the ice melt than estimated by traditional models.
Data are available from the authors by request.
GK, IA, and NG conceived the study; IA, RZ, and GK designed and performed the field experiments; GK developed the model; GK, IA, VK, and NG performed field data analysis; GK wrote the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
The study is a part of the research project “IceBound” supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG Project KI-853/11-1, KI-853/11-2). Additional support by the DFG Project KI-853/13-1 is gratefully appreciated by Georgiy Kirillin. Field work and data analysis were carried out within the framework of LIN SB RAS State Task No. 0345-2019-0008 and additionally supported by project ISDCT SB RAS No. 0348-2020-0012.
This research has been supported by the Deutsche Forschungsgemeinschaft (DFG grant nos. KI-853/11-1, KI-853/11-2, and
KI-853/13-1).
The publication of this article was funded by the
Open Access Fund of the Leibniz
Association.
This publication is also funded by the German Research Foundation (DFG).
This paper was edited by Louise Slater and reviewed by two anonymous referees.
Aslamov, I., Kozlov, V., Kirillin, G., Mizandrontsev, I., Kucher, K., Makarov, M., Gornov, A. Y., and Granin, N.: Ice–water heat exchange during ice growth in Lake Baikal, J. Great Lakes Res., 40, 599–607, 2014a. a, b, c, d, e, f, g, h
Aslamov, I., Kozlov, V., Mizandrontsev, I., Kucher, K., and Granin, N.: Estimate of Heat Flux at the Ice—Water Interface in Lake Baikal from Experimental Data, Dokl. Earth Sci., 457, 982–985, 2014b. a
Aslamov, I., Kozlov, V., Kirillin, G., Mizandrontsev, I., Kucher, K., Makarov, M., and Granin, N.: A study of heat transport at the ice base and structure of the under-ice water layer in Southern Baikal, Water Resour., 44, 428–441, 2017. a, b, c, d
Barnes, D. and Hobbie, J.: Rate of melting at the bottom of floating ice, in: Geological Survey Research: Short Papers in the Geological Sciences, Geol. Surv. Prof. Pap., vol. 400, US Geological Survey, Govt. Print. Off., Washington, D.C., B392–B394, 1960. a, b
Bluteau, C. E., Pieters, R., and Lawrence, G. A.: The effects of salt exclusion during ice formation on circulation in lakes, Environ. Fluid Mech., 17, 579–590, 2017. a
Carmack, E., Polyakov, I., Padman, L., Fer, I., Hunke, E., Hutchings, J., Jackson, J., Kelley, D., Kwok, R., Layton, C., Melling, H., Perovich, D., Persson, O., Ruddick, B., Timmermans, M.-L., Toole, J., Ross, T., Vavrus, S., and Winsor, P.: Toward quantifying the increasing role of oceanic heat in sea ice loss in the new Arctic, B. Am. Meteorol. Soc., 96, 2079–2105, 2015. a
Deardorff, J. W.: Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection, J. Atmos. Sci., 27, 1211–1213, 1970. a
Dougherty, J.: The anisotropy of turbulence at the meteor level, J. Atmos. Terr. Phys., 21, 210–213, 1961. a
Farmer, D. M.: Penetrative convection in the absence of mean shear, Q. J. Roy. Meteorol. Soc., 101, 869–891, 1975. a
Farmer, D. M. and Carmack, E.: Wind mixing and restratification in a lake near the temperature of maximum density, J. Phys. Oceanogr., 11, 1516–1533, 1981. a
Gallaher, S. G., Stanton, T. P., Shaw, W. J., Cole, S. T., Toole, J. M., Wilkinson, J. P., Maksym, T., and Hwang, B.: Evolution of a Canada Basin ice-ocean boundary layer and mixed layer across a developing thermodynamically forced marginal ice zone, J. Geophys. Res.-Oceans, 121, 6223–6250, 2016. a
Gargett, A., Osborn, T., and Nasmyth, P.: Local isotropy and the decay of turbulence in a stratified fluid, J. Fluid Mech., 144, 231–280, 1984. a
Gill, A. E.: Atmosphere-Ocean dynamics (International Geophysics Series), Academic Press, New York, 1982. a
Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S., and Persson, P. O. G.: Similarity theory based on the Dougherty–Ozmidov length scale, Q. J. Roy. Meteorol. Soc., 141, 1845–1856, 2015. a
Granin, N., Jewson, D., Gnatovsky, R. Y., Levin, L., Zhdanov, A., Gorbunova, L., Tsekhanovsky, V., Doroschenko, L., and Mogilev, N. Y.: Turbulent mixing under ice and the growth of diatoms in Lake Baikal, Internationale Vereinigung für theoretische und angewandte Limnologie: Verhandlungen, 27, 2812–2814, 2000. a
Hamblin, P. and Carmack, E.: On the rate of heat transfer between a lake and an ice sheet, Cold Reg. Sci. Technol., 18, 173–182, 1990. a
Hampton, S. E., Izmest'eva, L. R., Moore, M. V., Katz, S. L., Dennis, B., and Silow, E. A.: Sixty years of environmental change in the world's largest freshwater lake–Lake Baikal, Siberia, Global Change Biol., 14, 1947–1958, 2008. a
Huang, W., Zhang, J., Leppäranta, M., Li, Z., Cheng, B., and Lin, Z.: Thermal structure and water-ice heat transfer in a shallow ice-covered thermokarst lake in central Qinghai-Tibet Plateau, J. Hydrol., 578, 124122, https://doi.org/10.1016/j.jhydrol.2019.124122, 2019. a
Jackson, J., Carmack, E., McLaughlin, F., Allen, S. E., and Ingram, R.: Identification, characterization, and change of the near-surface temperature maximum in the Canada Basin, 1993–2008, J. Geophys. Res.-Oceans, 115, C05021, https://doi.org/10.1029/2009JC005265, 2010. a
Jackson, J. M., Williams, W. J., and Carmack, E. C.: Winter sea-ice melt in the Canada Basin, Arctic Ocean, Geophys. Res. Lett., 39, L03603, https://doi.org/10.1029/2011GL050219, 2012. a
Jewson, D. H., Granin, N. G., Zhdanov, A. A., and Gnatovsky, R. Y.: Effect of snow depth on under-ice irradiance and growth of Aulacoseira baicalensis in Lake Baikal, Aquat. Ecol., 43, 673–679, 2009. a
Kirillin, G., Leppäranta, M., Terzhevik, A., Granin, N., Bernhardt, J., Engelhardt, C., Efremova, T., Golosov, S., Palshin, N., Sherstyankin, P., Zdorovennova, G., and Zdorovennov, R.: Physics of seasonally ice-covered lakes: a review, Aquat. Sci., 74, 659–682, 2012. a, b, c, d, e
Kirillin, G., Aslamov, I., Leppäranta, M., and Lindgren, E.: Turbulent mixing and heat fluxes under lake ice: the role of seiche oscillations, Hydrol. Earth Syst. Sci., 22, 6493–6504, https://doi.org/10.5194/hess-22-6493-2018, 2018. a, b, c, d, e, f, g
Kolmogorov, A. N.: The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers, Dokl. Akad. Nauk SSSR, 30, 299–303, 1941. a
Leppäranta, M.: A growth model for black ice, snow ice and snow thickness in subarctic basins, Hydrol. Res., 14, 59–70, 1983. a
Lien, R.-C. and D'Asaro, E. A.: The Kolmogorov constant for the Lagrangian velocity spectrum and structure function, Phys. Fluids, 14, 4456–4459, 2002. a
Magnuson, J. J., Robertson, D. M., Benson, B. J., Wynne, R. H., Livingstone, D. M., Arai, T., Assel, R. A., Barry, R. G., Card, V., Kuusisto, E., Granin, N. G., Prowse, T. D., Stewart, K. M., and Vuglinski, V. S.: Historical trends in lake and river ice cover in the Northern Hemisphere, Science, 289, 1743–1746, 2000. a
McPhee, M. G.: Turbulent heat flux in the upper ocean under sea ice, J. Geophys. Res.-Oceans, 97, 5365–5379, 1992. a, b, c
Mironov, D., Terzhevik, A., Kirillin, G., Jonas, T., Malm, J., and Farmer, D.: Radiatively driven convection in ice-covered lakes: Observations, scaling, and a mixed layer model, J. Geophys. Res.-Oceans, 107, 7-1–7-16, https://doi.org/10.1029/2001JC000892, 2002. a, b, c, d, e
Monin, A. and Ozmidov, R.: Oceanic Turbulence, Gidrometeoizdat, Leningrad, 1981. a
Nan, L., Tuo, Y.-C., Yun, D., Jia, L., Liang, R.-F., and An, R.-D.: Heat transfer at ice-water interface under conditions of low flow velocities, J. Hydrodynam. B, 28, 603–609, 2016. a
Ozmidov, R.: On the turbulent exchange in a stably stratified ocean, Izv. Acad. Sci. USSR, Atmos. Ocean. Phys., 1, 493–497, 1965. a
Perovich, D. K. and Richter-Menge, J. A.: Loss of sea ice in the Arctic, Annu. Rev. Mar. Sci., 1, 417–441, 2009. a
Perovich, D. K., Richter-Menge, J. A., Jones, K. F., Light, B., Elder, B. C., Polashenski, C., Laroche, D., Markus, T., and Lindsay, R.: Arctic sea-ice melt in 2008 and the role of solar heating, Ann. Glaciol., 52, 355–359, 2011. a
Peterson, A. K., Fer, I., McPhee, M. G., and Randelhoff, A.: Turbulent heat and momentum fluxes in the upper ocean under Arctic sea ice, J. Geophys. Res.-Oceans, 122, 1439–1456, 2017. a, b
Pollard, R. T., Rhines, P. B., and Thompson, R. O.: The deepening of the wind-mixed layer, Geophys. Astrophys. Fluid Dynam., 4, 381–404, 1972. a, b
sputnik.irk.ru: Irkutsk Center for remote sensing, available at: http://sputnik.irk.ru/, last access: 20 November 2019. a
Stull, R. B.: An Introduction to Boundary Layer Meteorology, Kluwer, Dordrecht, Boston, London, 2012. a
Tranvik, L. J., Downing, J. A., Cotner, J. B., Loiselle, S. A., Striegl, R. G., Ballatore, T. J., Dillon, P., Finlay, K., Fortino, K., Knoll, L. B., Kortelainen, P. L., Kutser, T., Larsen, S., Laurion, I., Leech, D. M., McCallister, S. L., McKnight, D. M., Melack, J. M., Overholt, E., Porter, J. A., Prairie, Y., Renwick, W. H., Roland, F., Sherman, B. S., Schindler, D. W., Sobek, S., Tremblay, A., Vanni, M. J., Verschoor, A. M., von Wachenfeldt, E., and Weyhenmeyer, G. A.: Lakes and reservoirs as regulators of carbon cycling and climate, Limnol. Oceanogr., 54, 2298–2314, 2009. a
Turner, J. S.: Buoyancy Effects in Fluids, Cambridge University Press, Cambrigde, 1979. a
Volkov, S., Bogdanov, S., Zdorovennov, R., Zdorovennova, G., Terzhevik, A., Palshin, N., Bouffard, D., and Kirillin, G.: Fine scale structure of convective mixed layer in ice-covered lake, Environ. Fluid Mech., 19, 751–764, https://doi.org/10.1007/s10652-018-9652-2, 2019. a, b, c, d
Wiles, P. J., Rippeth, T. P., Simpson, J. H., and Hendricks, P. J.: A novel technique for measuring the rate of turbulent dissipation in the marine environment, Geophys. Res. Lett., 33, L21608, https://doi.org/10.1029/2006GL027050, 2006. a
Yang, B., Young, J., Brown, L., and Wells, M.: High-Frequency Observations of Temperature and Dissolved Oxygen Reveal Under-Ice Convection in a Large Lake, Geophys. Res. Lett., 44, 12–218, 2017. a
Zhdanov, A., Gnatovskii, R., Granin, N., Blinov, V., Aslamov, I., and Kozlov, V.: Variations of under-ice currents in Southern Baikal by data of 2012–2016, Water Resour., 44, 442–452, 2017. a
Zilitinkevich, S. and Mironov, D. V.: A multi-limit formulation for the equilibrium depth of a stably stratified boundary layer, Bound.-Lay. Meteorol., 81, 325–351, 1996. a, b