Technical note: The beneficial role of a natural permeable layer in slope stabilization by drainage trenches

Slope stabilization through drainage trenches is a classic approach in geotechnical engineering. Considering the low hydraulic conductivity of the soils in which this measure is usually adopted, a major constraint to the use of trenches is the time required to obtain a significant pore pressure decrease, here called “time lag”. In fact, especially when the slope safety factor is small, the use of drainage trenches may be a risky approach due to the probability that slope deformations will damage the system well before it will become fully operative.

However, this paper shows that the presence of persistent permeable natural soil layers can provide a significant benefit by increasing drainage efficiency and reducing time lag. As a matter of fact, any permeable layer that is intercepted by trenches may operate as part of the global hydraulic system, reducing the drainage paths.

A simplified approach to designing a drainage system that accounts for the presence of a persistent permeable layer is proposed. This approach, which can exploit solutions available in the literature for parallel drainage trenches, has been validated by numerical analyses.

1 Introduction

The stabilization of deep landslides in clay is one of the greatest challenges to engineers due to the high cost and the unreliability of many structural solutions. Often, the only available approach is deep drainage, which can lead to some shear strength increase through a generalized pore pressure decrease. Available solutions (Hutchinson, 1977; Bromhead, 1984; Stanic, 1984; Desideri et al., 1997; Pun and Urciuoli, 2008; Urciuoli and Pirone, 2013) include the use of deep parallel trenches (and of deeper drainage panels as well), which are also dealt with in this paper, and tubular drains in a homogeneous soil.

Considering the fine-grained nature of the soil, a major constraint to slope stabilization by draining trenches is the long time required to obtain a significant pore pressure decrease (time lag). In particular, when the slope is characterized by a small safety factor or is subjected to slow movements (Urciuoli, 1998), the use of draining trenches is in fact problematic due to the probability that slope deformations will damage the system well before it will become fully operative, thus cancelling out its potential effectiveness. However, the higher the depth of the trenches (or of drainage panels), the higher the probability that these intercept even thin soil layers of higher hydraulic conductivity at an intermediate depth between the ground surface and the slip surface. This would be a favourable condition since the incorporation of such layers in the drainage system may play a highly beneficial role in both the time to attain the final steady-state condition and the system efficiency.

The scope of this paper is restricted to an examination of the influence on the drainage system of a pre-existing permeable soil layer parallel to the ground surface.

2 The basic model

The solutions presented below are based on the following assumptions:

• The groundwater flow is two-dimensional.

• Each soil layer is homogeneous, isotropic and characterized by a linear elastic constitutive law.

• Total stresses are constant during the consolidation process (this allows the analysis of the hydraulic and of the mechanical soil responses to be uncoupled).

The governing equation of the problem (i.e. soil consolidation induced by the draining elements) is the following:

$$\begin{array}{}\text{(1)}& h_t-c_v^{\mathrm{2}\mathrm{D}}\left(h_{xx}+h_{yy}\right)=\mathrm{0},\end{array}$$

where $h=\mathit{\zeta }+\frac{u}{{\mathit{\gamma }}_{\mathrm{w}}}$ and $c_v^{\mathrm{2}\mathrm{D}}=\frac{KE}{\mathrm{2}\left(\mathrm{1}+\mathit{\nu }\right)\left(\mathrm{1}-\mathrm{2}\mathit{\nu }\right){\mathit{\gamma }}_{\mathrm{w}}}$.

The technical literature reports solutions concerning the case of parallel draining trenches and of tubular drains in homogeneous soils, which are generally presented in the form of dimensionless design charts, providing the average efficiency, $\stackrel{\mathrm{‾}}{E}\left(t,\mathrm{\Gamma }\right)$, along the slip surface Γ:

$$\begin{array}{}\text{(2)}& \stackrel{\mathrm{‾}}{E}\left(t,\mathrm{\Gamma }\right)={\displaystyle \frac{u\left(\mathrm{0},\mathrm{\Gamma }\right)-\stackrel{\mathrm{‾}}{u}(t,\mathrm{\Gamma })}{u\left(\mathrm{0},\mathrm{\Gamma }\right)}}.\end{array}$$

In Eq. (2), u(0,Γ) is the initial pore pressure on the slip surface, Γ, and $\stackrel{\mathrm{‾}}{u}\left(t,\mathrm{\Gamma }\right)$ is the average pore pressure at time t modified by the draining elements; u(0,Γ)is generally assumed to be hydrostatic. During the consolidation phase, pore pressures decrease towards the minimum steady-state value $\stackrel{\mathrm{‾}}{u}(\mathrm{\infty },\mathrm{\Gamma })$, which is attained at time t→∞ when the efficiency $\stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty },\mathrm{\Gamma }\right)$ reaches the highest value.

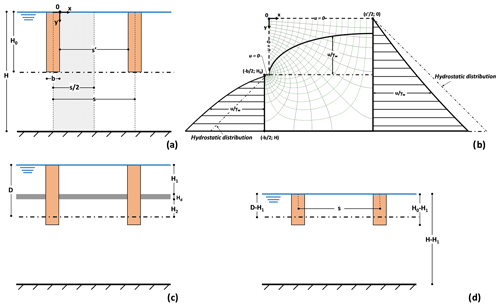
Figure 1 (a) Schematic representation of the case at hand. (b) Flow lines and equipotential lines in homogeneous soil; piezometric heads along the vertical axes at the middle of the trench, at the centre line between two adjacent trenches and on the horizontal plane at depth of trench bottom. (c) Scheme with an intermediate permeable layer. (d) Equivalent scheme with a water film at the depth of the uppermost boundary of layer d.

The available solutions for parallel trenches, featured by a thickness H₀ and a width b, consider the soil volume between the two axes of symmetry, which respectively coincide with the middle of a trench and the centre line between two adjacent trenches (Fig. 1a). This volume is delimited by the ground surface and by an impermeable bottom surface located at the distance H from the ground surface. The ground and bottom surfaces are both horizontal: the slope angle is indeed assumed to play a negligible role in the hydraulic process (Aloi et al., 2019). The slip surface Γ is a horizontal plane as well, located at depth D. In this paper it is assumed to be coincident with the base of the trenches (D=H₀).

A key hypothesis, which strongly affects the solution, is the presence of a permanent film of water at the ground surface (Burghignoli and Desideri, 1987; D'Acunto and Urciuoli, 2006, 2010; D'Acunto et al., 2007). However, due to local formation of water ponding and saturation of vertical cracks in the ground, often this is not far from the truth, at least during the wet season. Based on this assumption, the pore pressure decrease is uniquely due to rotation of the flow lines towards the drainage trenches. Pore pressures in the zone between parallel trenches are then at any time less than hydrostatic (Fig. 1b). In contrast, beyond the bottom of the trenches, the upward direction of the flow lines leads to a pore pressure distribution higher than hydrostatic. It is just for this reason that the drains should always reach a depth close to the slip surface.

3 Influence of a permeable layer located at an intermediate depth between ground and slip surface

3.1 Time of consolidation

As outlined above, the presence of one or more persistent permeable layers in the soil body to be stabilized (a not unlikely situation in deep clay deposits to be stabilized with draining panels) may play a highly beneficial role in time lag and the effectiveness of the drainage system.

Table 1 Examined cases studied with FEM.

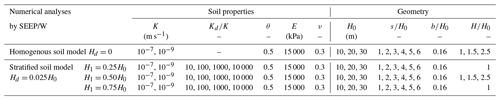
The influence of a layer parallel to the ground surface, here indicated as the “draining layer d”, featured by a thickness H_d as in Fig. 1c, has been investigated by FEM analyses using the code SEEP^® (GEO-SLOPE Int. Ltd., 2012). The cases examined in this paper are indicated in Table 1; the results of the analyses are shown in a dimensionless form.

The data show that the presence of the permeable layer allows a considerable shortening of the time lag, here represented by the time factor, T₉₀, corresponding to an efficiency $\stackrel{\mathrm{‾}}{E}\left(t_{\mathrm{90}},\mathrm{\Gamma }\right)=\mathrm{90}$ % of the average steady-state efficiency $\stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty },\mathrm{\Gamma }\right)$:

$$\begin{array}{}\text{(3)}& T_{\mathrm{90}}={\displaystyle \frac{c_v^{\mathrm{2}\mathrm{D}}{t}_{\mathrm{90}}}{H_{\mathrm{0}}^{\mathrm{2}}}}.\end{array}$$

The value of t₉₀ in Eq. (3) has been obtained by a numerical integration of Eq. (1), being the time at which $\stackrel{\mathrm{‾}}{E}(t,\mathrm{\Gamma })=\mathrm{0.90}\cdot \stackrel{\mathrm{‾}}{E}(\mathrm{\infty },\mathrm{\Gamma })$ (see Eq. 2).

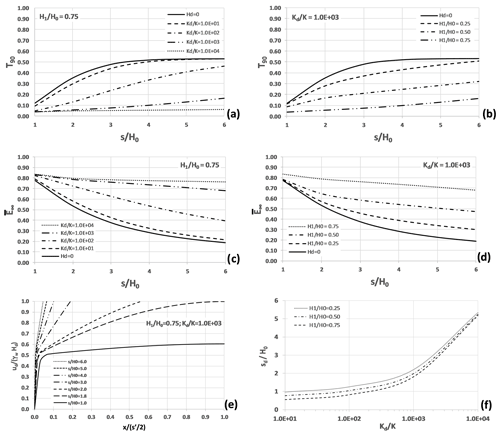
Figure 2 Results of the FEM analyses (assuming H=H₀). Dimensionless time, T₉₀, as a function of trench spacing and of (a) K_d∕K ratio for $H_{\mathrm{1}}/H_{\mathrm{0}}=\mathrm{0.75}$ and (b) H₁∕H₀ ratio for $K_d/K=\mathrm{1000}$. Average steady-state efficiency as a function of trench spacing and (c) K_d∕K ratio for $H_{\mathrm{1}}/H_{\mathrm{0}}=\mathrm{0.75}$ and (d) H₁∕H₀ ratio for $K_d/K=\mathrm{1000}$. (e) Dimensionless pore pressure over the lowermost boundary of layer d, u_d∕(γ_wH_d), as a function of $x/(s^{\prime }/\mathrm{2})$ and s∕H₀, for $K_d/K=\mathrm{1000}$ and $H_{\mathrm{1}}/H_{\mathrm{0}}=\mathrm{0.75}$. (f) Values of s_d∕H₀ as a function of K_d∕K and H₁∕H₀.

Figure 2a and b, which report some results concerning the horizontal plane located at depth D=H₀, suggest quite a rapid attainment of $\stackrel{\mathrm{‾}}{E}(t_{\mathrm{90}},\mathrm{\Gamma })$, which is a crucial issue of the design. For significant values of trench spacing in the practice (i.e. $s/H_{\mathrm{0}}<\mathrm{3}$), the following considerations may be drawn: (i) for $H_{\mathrm{1}}/H_{\mathrm{0}}=\mathrm{0.75}$ and $K_d/K=\mathrm{100}$ (Fig. 2a), the dimensionless time T₉₀ ranges between one-half and one-third of the value that would be obtained in the absence of the draining layer; (ii) for $K_d/K=\mathrm{1000}$ (Fig. 2b), T₉₀ significantly decreases with depth of the layer d (for $H_{\mathrm{1}}/H_{\mathrm{0}}=\mathrm{0.75}$, it drops to about 20 % of the value obtainable in homogenous soils).

3.2 Steady-state condition

The presence of a permeable layer allows higher values of $\stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty },\mathrm{\Gamma }\right)$ to be obtained, and sooner than in homogeneous soils. Some significant data are provided:

• i.

  Figure 2c, shows the steady-state efficiency for $H_{\mathrm{1}}/H_{\mathrm{0}}=\mathrm{0.75}$ reported as a function of the ratio K_d∕K and of trench spacing. As shown, the higher the hydraulic conductivity of the draining layer, the higher the efficiency (as an example, for $K_d/K=\mathrm{1000}$ and $s/H_{\mathrm{0}}=\mathrm{3}$ it practically doubles). A major effect of layer d is in fact diversion of a significant part of water coming from the ground surface towards the trench, thus strongly reducing water flow towards the slip surface.

• ii.

  Figure 2d shows the efficiency for $K_d/K=\mathrm{1000}$ reported as a function of depth of layer d and trench spacing. The figure shows that it increases as the dimensionless distance, H₁∕H₀, increases. The effect of layer d is a strong pore pressure reduction at depth H₁. As a consequence, pore pressure decrease, due to the action of layer d, increases with its depth.

• iii.

  Figure 2e shows the non-dimensional pore pressure distribution, u_d, along the lower boundary of the draining layer d plotted as a function of trench spacing for $H_{\mathrm{1}}/H_{\mathrm{0}}=\mathrm{0.75}$ and $K_d/K=\mathrm{1000}$. Near the trench boundary, the pressure head is less than H_d; hence, a free water surface forms in the layer d (here water can move towards the trench only below this surface, where pore pressures are positive).

A simplified approach to predict the steady-state condition

In the following, a simplified model for the optimization of the design is briefly described. A very efficient working condition is achieved if, at the centre line between two adjacent trenches, the atmospheric pressure is attained at the uppermost point of layer d.

The first step in the design of the drainage system is just creating the conditions for full layer activation. This is obtained when the spacing, s, of the trenches is equal to the value s_d, according to the following expression:

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{s_d}{H_{\mathrm{0}}}}=f\left({\displaystyle \frac{H_d}{H_{\mathrm{0}}}},{\displaystyle \frac{H_{\mathrm{1}}}{H_{\mathrm{0}}}},{\displaystyle \frac{K_d}{K}}\right).\end{array}$$

The values of s_d∕H₀ in Eq. (4) have been obtained from the results of the numerical integration of Eq. (1). These have been reported in Fig. 2f, which shows the dependency of s_d∕H₀ on K_d∕K and H₁∕H₀, having fixed H_d∕H₀.

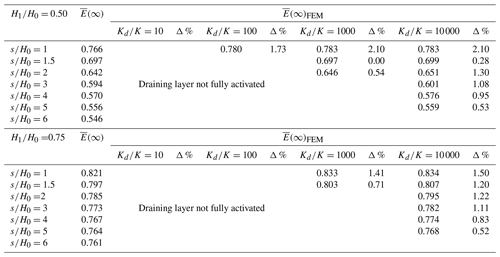
Table 2 Comparison among steady-state efficiency values computed by Eq. (8), $\stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty }\right)$, and FEM analyses, $\stackrel{\mathrm{‾}}{E}(\mathrm{\infty }{)}_{\mathrm{FEM}}\cdot \left(\mathrm{\Delta }=\left|\frac{\stackrel{\mathrm{‾}}{E}{\left(\mathrm{\infty }\right)}_{\mathrm{FEM}}-\stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty }\right)}{\stackrel{\mathrm{‾}}{E}{\left(\mathrm{\infty }\right)}_{\mathrm{FEM}}}\right|\mathit{\%}\right)$. Only results obtained for fully drained activation are reported (s≤s_d).

In case of full activation of layer d, the response of the entire draining system may be analysed by a simplified approach. Since the fluid pressure at the uppermost boundary of the layer d is equal to the atmospheric pressure (or to a small amount of suction, especially near the trench boundary), a water film may be fictitiously assumed at the same depth (Fig. 1d). This obviously leads to a generalized pore pressure decrease in the lowermost soil. In the following, any parameter referring to this fictitious condition will be indicated by the apex ^∗.

The values of ${\stackrel{\mathrm{‾}}{u}}^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)$ and ${\stackrel{\mathrm{‾}}{E}}^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)$ may be obtained from the well known dimensionless solutions for the case of parallel trenches in homogeneous soil, as a function of spacing (see the simplified scheme in Fig. 1d). The steady-state efficiency is

$$\begin{array}{}\text{(5)}& E^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)={\displaystyle \frac{u^{\ast }\left(\mathrm{0},\mathrm{\Gamma }\right)-{\stackrel{\mathrm{‾}}{u}}^{\ast }(\mathrm{\infty },\mathrm{\Gamma })}{u^{\ast }\left(\mathrm{0},\mathrm{\Gamma }\right)}},\end{array}$$

thus

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\stackrel{\mathrm{‾}}{u}}^{\ast }(\mathrm{\infty },\mathrm{\Gamma })& =u^{\ast }\left(\mathrm{0},\mathrm{\Gamma }\right)\left(\mathrm{1}-E^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)\right)\\ & ={\mathit{\gamma }}_{\mathrm{w}}\left(D-H_{\mathrm{1}}\right)\left(\mathrm{1}-E^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)\right).\end{array}\end{array}$$

It is worth noting that

$$\begin{array}{}\text{(7)}& \stackrel{\mathrm{‾}}{u}\left(\mathrm{\infty },\mathrm{\Gamma }\right)={\stackrel{\mathrm{‾}}{u}}^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)\end{array}$$

and

$$\begin{array}{}\text{(8)}& \stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty },\mathrm{\Gamma }\right)={\displaystyle \frac{u\left(\mathrm{0},\mathrm{\Gamma }\right)-{\stackrel{\mathrm{‾}}{u}}^{\ast }(\mathrm{\infty },\mathrm{\Gamma })}{u\left(\mathrm{0},\mathrm{\Gamma }\right)}}.\end{array}$$

The values obtained from Eq. (8), through the value of ${\stackrel{\mathrm{‾}}{u}}^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)$ provided by mentioned solutions, have been compared to those obtained by FEM (Table 2). The good agreement allows the proposed method to be validated. It is worth mentioning that the solid lines in Fig. 2c and d for H_d=0 are just those that are reported in the design charts.

4 Conclusions and final considerations

The aim of this paper is to demonstrate that the presence of soil layers of higher permeability, a not unlikely condition in some deep landslides in clay, may be exploited to improve the efficiency of systems of drainage trenches for slope stabilization. Once the depth of the trenches, which should reach the slip surface, is established, the selection of proper spacing may create a hydraulic system in which such layers can work as additional drains. The problem has been examined for the case that a unique permeable layer is present at an elevation higher than the bottom of the trenches.

The results of numerical analyses show that it significantly speeds up the consolidation process triggered by drainages, also leading to higher steady efficiency of the system. However, as mentioned in the Introduction, in many practical cases the design must take into account the time requested to achieve an adequate effective stress and safety factor increase. In these cases, trench spacing should be governed by the T₉₀ value.

If pore pressures in the draining layer do not exceed the atmospheric pressure, a hydraulic disconnection forms between the two parts of the landslide body located above and below the layer, respectively. In such a way, the water film which is normally assumed at the ground surface ideally moves to the depth of the draining layer. This simple consideration allows the employment of the design charts available for the design of drainage trenches in homogeneous soils in the equivalent scheme characterized by groundwater level located at the depth of the draining layer, in order to calculate the final system efficiency.

It is worth mentioning that the hydraulic continuity of layer d is a fundamental condition for the design. Considering the variability and the unpredictability of many natural situations, proper investigations to check the validity of such an assumption are warmly recommended. In particular, the adoption of such a stabilization measure should always be managed through the “observational method”, i.e. by monitoring the system response in order to (i) check the validity of the design and (ii) adopt proper modifications to it due to unexpected or neglected factors. The installation of piezometers is an obvious measure to check in real time the efficiency of the drainage system (especially during the critical rainy season). The piezometers should be installed both in proximity to the slip surface (near and far from the trenches) and, if possible depending on thickness, in the permeable layer. This will allow the full activation of the permeable layer to be verified.

Appendix A: List of symbols

b	width of the trench
$c_v^{\mathrm{2}\mathrm{D}}$	2D coefficient of consolidation
d	draining layer
D	depth of the slip surface
E	Young modulus of the soil
$\stackrel{\mathrm{‾}}{E}(t,\mathrm{\Gamma })$	average efficiency of the draining trenches at time t along the sliding surface Γ
$\stackrel{\mathrm{‾}}{E}(\mathrm{\infty },\mathrm{\Gamma })$	average steady-state efficiency of the draining trenches along the sliding surface Γ
${\stackrel{\mathrm{‾}}{E}}^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)$	average steady-state efficiency of the draining trenches along the sliding surface Γ according to the simplified approach (full activation of layer d)
γw	unit weight of water
Γ	slip surface
h	total head
ht	first derivative of total head h with respect to time t
hxx	second derivative of total head h with respect to abscissa x
hyy	second derivative of total head h with respect to ordinate y
H	depth of the impermeable bottom surface
H0	depth of the base of trench
H1	depth of the draining layer d
Hd	thickness of the draining layer d
K	coefficient of hydraulic conductivity
Kd	coefficient of hydraulic conductivity of the draining layer d
θ	soil moisture
s	spacing between trenches
sd	spacing between trenches creating the conditions for full activation of the draining layer d
s′	distance between the boundaries of the trenches
ν	Poisson ratio of the soil
t	time
t90	dimensional time corresponding to $\stackrel{\mathrm{‾}}{E}\left(t,\mathrm{\Gamma }\right)=\mathrm{90}$ % of the average steady-state efficiency $\stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty },\mathrm{\Gamma }\right)$
T90	dimensionless time factor for $\stackrel{\mathrm{‾}}{E}\left(t,\mathrm{\Gamma }\right)=\mathrm{90}$ % of the average steady-state efficiency $\stackrel{\mathrm{‾}}{E}\left(\mathrm{\infty },\mathrm{\Gamma }\right)$
u	pore pressure
ud	pore pressure at the base of the draining layer d
u(0,Γ)	initial pore pressure (time t=0) on the slip surface Γ
$u^{\ast }\left(\mathrm{0},\mathrm{\Gamma }\right)$	initial pore pressure (time t=0) on the slip surface Γ according to the simplified approach (full activation of the draining layer d)
$\stackrel{\mathrm{‾}}{u}\left(t,\mathrm{\Gamma }\right)$	average pore pressure at time t on the slip surface Γ, modified by drainage trenches
$\stackrel{\mathrm{‾}}{u}(\mathrm{\infty },\mathrm{\Gamma })$	average steady-state pore pressure on the slip surface Γ, modified by drainage trenches
${\stackrel{\mathrm{‾}}{u}}^{\ast }\left(\mathrm{\infty },\mathrm{\Gamma }\right)$	average steady-state pore pressure on the slip surface Γ, modified by drainage trenches according to the simplified approach (full activation of the draining layer d)
ζ	elevation head