Reflection tomography of time-lapse GPR data for studying dynamic unsaturated flow phenomena

Ground-penetrating radar (GPR) reflection tomography algorithms allow non-invasive monitoring of water content changes resulting from flow in the vadose zone. The approach requires multi-offset GPR data that are traditionally slow to collect. We automate GPR data collection to reduce the survey time significantly, thereby making this approach to hydrologic monitoring feasible. The method was evaluated using numerical simulations and laboratory experiments that suggest reflection tomography can provide water content estimates to within 5 % vol vol⁻¹–10 % vol vol⁻¹ for the synthetic studies, whereas the empirical estimates were typically within 5 %–15 % of measurements from in situ probes. Both studies show larger observed errors in water content near the periphery of the wetting front, beyond which additional reflectors were not present to provide data coverage. Overall, coupling automated GPR data collection with reflection tomography provides a new method for informing models of subsurface hydrologic processes and a new method for determining transient 2-D soil moisture distributions.

1 Introduction

Preferential flow is ubiquitous in the vadose zone, occurring under a wide variety of conditions and over a broad range of scales (Nimmo, 2012). Reviews such as those by Hendrickx and Flury (2001) and Jarvis (2007) illustrate that a basic mechanistic understanding of preferential flow exists. Jarvis et al. (2016) point out, however, that we still lack models capable of reproducing empirical observations in the field and highlight the importance of non-invasive imaging techniques for improving this understanding. We suggest that ground-penetrating radar (GPR) reflection tomography could fill this need by quantitatively mapping changes in water content through space and time at the sub-meter scale.

Reflection GPR is commonly used to image subsurface structures, but is also well suited to understanding hydrologic variability due to the strong dependence of EM wave velocities on soil volumetric water content (Topp et al., 1980). As a result, GPR has been adapted to monitor variability in hydrologic processes at multiple scales through time and space in a variety of contexts (Buchner et al., 2011; Busch et al., 2013; Guo et al., 2014; Haarder et al., 2011; Lunt et al., 2005; Mangel et al., 2012, 2015b, 2017; Moysey, 2010; Saintenoy et al., 2007; Steelman and Endres, 2010; Vellidis et al., 1990). Note that GPR methods are not applicable in media with relatively high electrical conductivity.

While these studies have illustrated a variety of techniques for monitoring changes in water content within the subsurface, they have generally required assumptions to constrain the interpretation, such as the use of a priori information regarding subsurface structure (e.g., Lunt et al., 2005) or the GPR wave velocity (Haarder et al., 2011). These limitations arise from the fact that GPR data are recorded as energy arriving at the receiver antenna as a function of time. Inherent assumptions therefore exist in analyzing travel-time data collected with antennas separated by a fixed offset because both the distance traveled by the GPR wave to a reflector and the velocity of the GPR wave are unknown. It has been demonstrated that GPR data collected via a multi-offset survey can constrain both the depth to a moving wetting front and the water content behind the front over the course of an infiltration event (Gerhards et al., 2008; Mangel et al., 2012). The limitation of these studies, however, was that the authors assumed a 1-D flow system and that GPR data lacked information regarding lateral variability in soil moisture.

Extending multi-offset techniques (Forte and Pipan, 2017; Jaumann and Roth, 2018; Klenk et al., 2015; Lambot et al., 2004, 2009) to image flow in the vadose zone requires an increase in the speed at which these data can be collected and advanced processing methods that can combine thousands of measurements into spatially and temporally variable water content estimates. We have recently overcome the data collection problem by automating GPR data collection using a computer-controlled gantry, thereby reducing the data collection time for large multi-offset surveys from hours to minutes (Mangel et al., 2015a). Tomography and wave migration algorithms from the seismic literature have been available for decades (Baysal et al., 1983; Lafond and Levander, 1993; Sava and Biondi, 2004a, b; Stork, 1992; Yilmaz and Chambers, 1984) and are being continually adapted to GPR applications. For example, this work is made possible due to adaptation of the pre-stack migration algorithm (Leparoux et al., 2001) and adaptation of the reflection tomography algorithm (Bradford, 2006) to multi-offset GPR data. Subsequent studies have demonstrated the use of GPR reflection tomography for imaging static distributions of subsurface water content with great detail (Bradford, 2008; Bradford et al., 2009; Brosten et al., 2009). The combination of automated GPR data collection and reflection tomography makes time-lapse imaging of water content during infiltration a feasible means to study flow in the vadose zone.

The objective of this study is to evaluate reflection tomography of high-resolution GPR data as a tool for observing and characterizing unsaturated flow patterns during infiltration into a homogeneous soil. To evaluate the efficacy of the algorithm for resolving dynamic soil water content in 2-D, we first test the algorithm using numerical simulations and compare the results to true water content distributions. We then apply the algorithm to time-lapse GPR data collected during an infiltration and recovery event in a homogeneous soil and compare results to measurements from in situ soil moisture probes.

2 Methods

2.1 The reflection tomography algorithm

The goal of reflection tomography is to determine a velocity model that best aligns migrated reflection arrivals for a common reflection point across a set of source–receiver offsets. For brevity, we will limit our discussion here to the key ideas and methods of the tomography algorithm; we refer the reader to Stork (1992) for the original tomography algorithm and to Bradford (2006) for the application to GPR data.

The data required for this algorithm are an ensemble of common-midpoint (CMP) gathers collected along a path. Given that GPR data are a time-series record of electromagnetic energy arriving at a point in space, we must know the proper velocity structure to migrate the data and produce a depth-registered image of the GPR energy. Migration attempts to remove the hyperbolic trend of reflections with respect to antenna offset (Fig. 1a) by using the wave velocity to reposition reflections to the proper depth at which they occur. If CMP data are migrated with the correct velocity, reflections from layers in the subsurface are flattened as a function of offset (Fig. 1c). If the velocity estimate is incorrect, e.g., 10 % too slow (Fig. 1b) or 10 % too fast (Fig. 1d), the arrival is not flat and exhibits residual moveout (RMO). To solve for the velocity structure and properly migrate the data, the reflection tomography algorithm proceeds as follows (Bradford, 2006; Stork, 1992).

1. Generate a starting depth vs. velocity model.

2. Migrate the data with the starting velocity model and stack the data.

3. Pick horizons on the stacked image.

4. Perform ray tracing to the picked horizons with the velocity model.

5. Evaluate horizons for residual moveout.

6. Adjust the velocity model using reflection tomography.

7. Apply the revised velocity model using migration and quality check RMO.

8. Iterate at step three if necessary.

For this work, starting velocity models for the tomography algorithm are determined by smoothing results from 1-D velocity analysis of individual CMPs (Neidell and Taner, 1971). The reflection tomography algorithm then adjusts the velocity distribution until reflections in the depth-corrected (i.e., migrated) data line up to produce a reflection at a consistent depth across all traces in a CMP. Through sequential iterations of the tomographic inversion, the RMO metric is reduced on a global scale. For this work, the reflection tomography was performed using the SeisWorks software suite and Kirchhoff pre-stack depth migration (Yilmaz and Doherty, 2001).

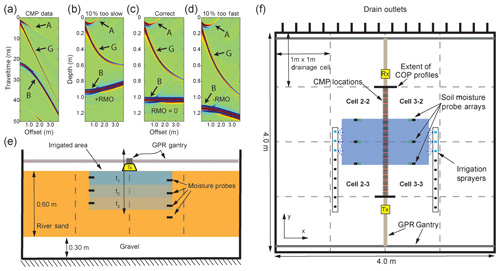
Figure 1 (a) Example CMP data showing the airwave (A), groundwave (G), and reflection from a layer (B). Data in (a) are migrated to form (b) a migrated gather with velocity 10 % too slow; (c) a migrated gather with correct velocity; and (d) a migrated gather with velocity 10 % too fast. Panel (e) shows a cross section of the experiment at y=2.0 m where t₁, t₂, and t₃ are arbitrary times during the infiltration. Panel (f) shows the plan view of the experiment. Note that the bottom of the sand layer is flat where GPR data collection occurs, i.e., on a boundary between drain cells, and pitched elsewhere toward cell drains.

2.2 Experimental setup and procedure

We used a 4 m × 4 m × 2 m tank for the controlled study of an unsaturated flow phenomenon with GPR (Fig. 1e, f). We filled the tank with a medium-grained sand to a depth of 0.60 m. Below the sand was a 0.30 m layer of gravel that acts as backfill for 16 individual drain cells that are pitched slightly toward central drains that route water to outlets on the outside of the tank. We constructed an automated data collection system to allow for the high-speed high-resolution collection of GPR data (Mangel et al., 2015a); the GPR gantry fits inside of the tank so the antennas are in contact with the sand surface. All GPR data described here were collected along the y axis of the tank at a fixed position of x=2.0 m, where the bottom of the tank is flat (Fig. 1e, f).

The automated system, which utilizes a 1000 MHz bistatic radar (Sensors and Software, Inc.), was operated to obtain 101 CMPs spaced at 0.02 m intervals between y=1.0 and 3.0 m. Each CMP consisted of 84 traces with offsets between 0.16 and 1.0 m at 0.01 m step size. Thus, a complete CMP data set for one observation time consists of almost 8500 individual GPR traces. With this configuration using the automated system, a CMP at a single location could be collected in 1.8 s with a total cycle of CMP data locations collected every 3.9 min.

GPR data collection occurred prior to irrigation to evaluate background conditions. Data collection continued during irrigation, which was applied at a flux of 0.125 cm min⁻¹ for a duration of 2.13 h. Spatial heterogeneity in the applied flux has been observed in laboratory testing of the irrigation equipment. Fifteen EC-5 soil moisture probes (METER, Inc.) logged volumetric water content at 10 s intervals during the experiment (Fig. 1e, f). Note that the soil moisture probes are located out of the plane of the GPR line by 0.5 m (Fig. 1f). GPR data collection continued for 40 min after the irrigation was terminated. In total, 45 complete sets of data were collected over the course of the 3 h experiment, yielding more than 500 000 GPR traces in the experimental data set.

2.3 Execution of the numerical simulations

We employed HYDRUS-2D (Simunek and van Genuchten, 2005) to simulate a theoretical and realistic hydrologic response to an infiltration event using two different initial conditions: (i) hydrostatic equilibrium leading to a water content distribution controlled by the soil water retention curve and (ii) a uniform soil with a water content of 0.07. We selected the Mualem–van Genuchten soil model (Mualem, 1976) and parameterized the model as follows based on hydraulic testing of the sand: residual water content (θ_r)=0.06, saturated water content (θ_s)=0.38, air-entry pressure (α)=0.058 cm⁻¹, shape parameter (n)=4.09, and saturated hydraulic conductivity (K_s)=4.6 cm min⁻¹. The hydraulic conductivity for the homogeneous model was reduced to 1 cm min⁻¹ to build a larger contrast of water content across the wetting front. For all HYDRUS simulations, we used a constant flux boundary condition of 0.125 cm min⁻¹ from y=1.6 to 2.4 m along the ground surface and set the model domain depth to 0.6 m, the length to 4.0 m, and the nominal cell size to 0.04 m. Remaining nodes at the surface were set to no-flow boundaries and lower boundary nodes were set to a seepage face with the pressure head equal to zero.

We calculated relative dielectric permittivity values for the GPR simulations by transforming water content values from HYDRUS-2D using the Topp equation (Topp et al., 1980). We used the magnetic permeability of free space for the entire model domain and set electrical conductivity of the soil to 1 mS m⁻¹. Although electrical conductivity changes as a function of the water content, these changes primarily influence wave attenuation, which is not significant or accounted for in the processing performed with the SeisWorks software.

We performed GPR simulations in MATLAB using a 2-D finite-difference time-domain code (Irving and Knight, 2006). The GPR model domain was set to 4.0 m long and 1.1 m high with a cell size of 0.002 m. The lower 0.3 m of the domain was set to a relative dielectric permittivity of 2.25 to represent the lower gravel layer and the upper 0.2 m was modeled as air to simulate the air–soil interface. Simulated data were collected as described in the section detailing the tank experiment. For quick computation, simulations were deployed on the Palmetto supercomputer cluster at Clemson University, where single-source simulations ran in 20 min using nodes with 8 CPUs and 32 GB of RAM.

3 Reflection tomography of simulations

The HYDRUS-2D output shows the development of an infiltrating wetting front for the two scenarios with differing initial conditions (Fig. 2a, f, k). For conditions prior to irrigation, the bottom of sand reflection (B) is horizontal on the common-offset profile (COP) data, indicating a constant velocity across the model domain (Fig. 2b). Additionally, the CMPs show identical hyperbolic moveout, i.e., the offset vs. travel-time relationship, indicating a homogeneous velocity across the model domain (Fig. 2c–e). The airwave and groundwave are also visible in the data, but are not analyzed or further discussed.

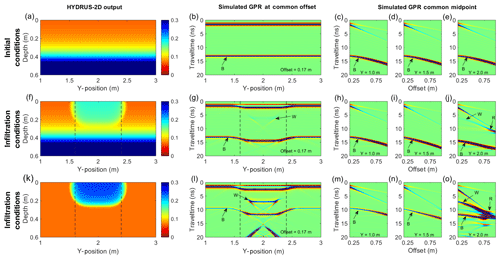
Figure 2 Panels (a), (f), and (k) show volumetric moisture distribution from HYDRUS-2D simulations used to generate simulated common-offset GPR data (b, g, l) and multi-offset GPR data (c–e, h–j, and m–o). Vertical dashed lines indicate the extent of the wetted surface. Annotated arrivals are the bottom of sand layer reflection (B), wetting front reflection (W), and refraction (R). Note that the base of the sand reflection (B) is caused by the boundary at 0.60 m depth between the sand and gravel, not the capillary rise shown in panels (a) and (f).

During infiltration, B is distorted at the center of the COP due to the decreased velocity caused by the infiltrating water (Fig. 2g, l). A reflection from the infiltrating wetting front (W) is faintly visible for the model with variable initial water contents (Fig. 2g) and comparatively strong for simulations with a dry background (Fig. 2l) due to different levels of dielectric contrast across the wetting front in each case. CMPs also indicate perturbations in the velocity field as the moveout changes dramatically when the wetted zone is encountered (Fig. 2h–j, m–o). A refraction is also observed on the CMPs, which is a rare occurrence considering that GPR wave velocity typically decreases with depth.

Prior to the onset of flow, the reflection tomography algorithm produces a uniform water content distribution that agrees with the arithmetic average of the true water content but does not capture the vertical gradation observed in Fig. 3a. This is because information regarding vertical velocity variations is absent; i.e., more reflectors at different depths are required to capture this variability. As a result, errors in the water content estimation exceed 10 % vol vol⁻¹ (Fig. 3d).

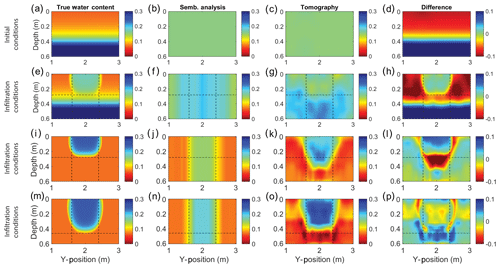
Figure 3 Panels (a), (e), (i), and (m) show true volumetric water content distributions from HYDRUS-2D. Panels (b), (f), (j), and (n) show starting models for the tomography derived from semblance analysis. Panels (c), (g), (k), and (o) show results of tomography of the simulated GPR data as volumetric water content. Difference plots (d), (h), (l), and (p) were calculated by subtracting the tomography results from the true water content distributions; red areas indicate volumetric moisture overestimation, while blue areas indicate volumetric moisture underestimation.

During infiltration, the wetting front is imaged relatively well for the case where the soil was initially dry (Fig. 3i–l), particularly as the plume advances deeper into the subsurface (Fig. 3m–p), where there is improved data coverage. The tomography algorithm overestimates the depth of the wetting front by roughly 0.10 m for the case presented in Fig. 3i–l, which is likely due to smoothing effects required to regularize the inversion or an error in the picking of the wetting front horizon. Considerable errors in the tomography results persist, however, with the results degrading further for the scenario with variable initial water content (Fig. 3e–h) given that reflection contrasts with the wetting front are weaker. The presence of an additional reflector, however, increases the ability of the tomography to resolve vertical variability, e.g., Fig. 2g vs. Fig. 2b. Overall, errors are reduced near reflectors to about 5 % vol vol⁻¹. These results suggest that water content changes resulting from unsaturated flow can be imaged and that as more information becomes available in the form of additional reflections, the tomography results improve.

4 Reflection tomography of experimental data

At initial conditions, the sand layer reflection (B) is visible at 10 ns travel-time in the COP collected over the imaging area (Fig. 4a). Normal hyperbolic moveout of (B) is observed on the CMPs (Fig. 4b, c, d). These results are qualitatively identical to observations from numerical simulations (Fig. 2b–e).

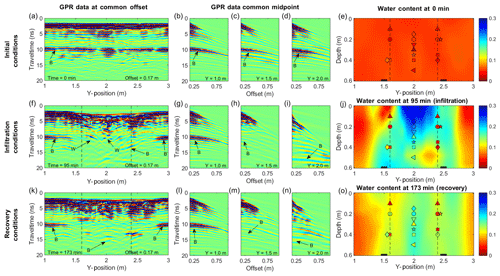
Figure 4 Panels (a, f, k) are common-offset GPR data collected during the experiment. Panels (b–d, g–i, and l–n) are CMP data collected during the experiment. Arrivals annotated are the sand layer reflection (B) and wetting front reflection (W). Panels (e, j, o) show tomography results for the corresponding GPR data. Vertical lines indicate the lateral extent of the wetted surface. Shapes correspond to the soil moisture data for the given y location in Fig. 5 and colors correspond to the measured soil moisture. Adjacent symbols are from probes that are located at different x locations but identical depths.

During infiltration, the water content of the sand layer increases substantially (Fig. 5) and longer travel times for the arrivals on the COP data are observed near the center of the tank (Figs. 4f, i). Rather than a coherent reflection for the wetting front (W) (Fig. 2l), multiple discrete reflections are present in the COP data (Fig. 4e, i, m), indicating a heterogeneous wetting of the soil. These reflections are difficult to identify on the CMPs given the complex moveout pattern (Fig. 4i), but are more easily identified in animations of COP projections of the data (included as a supplementary file). Analysis of the data was greatly aided by the animation of the data and the pre-stack migration algorithm, which stacks the data over all offsets to produce a coherent image of reflectors with an increased signal-to-noise ratio. Heterogeneous wetting of the soil is also very pronounced in the soil-moisture probe data, with many of the probes responding out of sequence with depth (Fig. 5). After irrigation, the soil-moisture probes show a decrease in the soil water content (Fig. 5) apart from one probe (Fig. 5c) and the GPR data show a slight decrease in the travel time to the bottom of sand reflection (Fig. 4k–n).

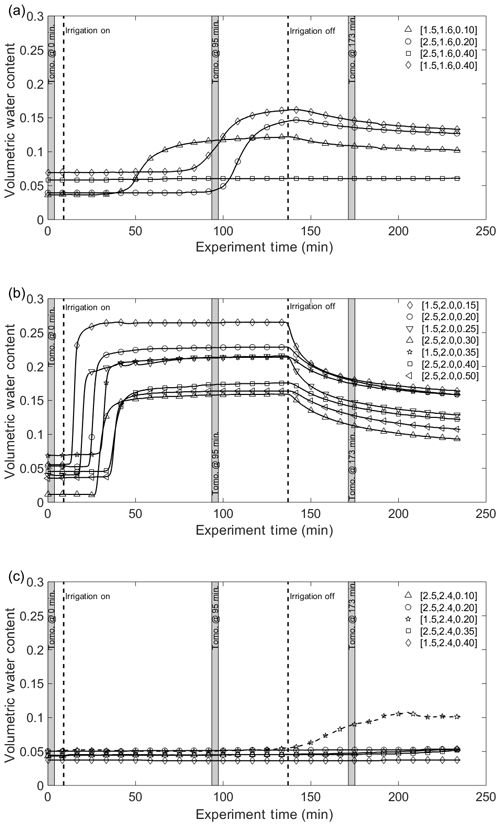
Figure 5 Soil moisture probe data from the in situ moisture probes along the GPR line at (a) y=1.6 m, (b) y=2.0 m, and (c) y=2.4 m. Vertical dashed lines indicate the start and stop of irrigation. Gray bars indicate the times when data in Fig. 4 were collected. Symbols for a given data set match those in Fig. 4e, j, and o. Soil moisture data were collected 60 min beyond the end of GPR data collection.

The tomographic imaging results from the initial GPR data set collected prior to irrigation agree with data from soil moisture probes, which indicates an average soil moisture of roughly 5 % during this time (Figs. 4e, 5). During infiltration and recovery, tomographic images of the tank show a wet zone at the center and relatively dry edges outside the irrigated area (Fig. 4j, o). Overall, the tomography results near the center of the tank are within 10 % vol vol⁻¹ of the soil moisture data and show a non-uniform wetting of the soil during infiltration that was not observed in the numerical study, suggesting the occurrence of preferential flow. Errors in the estimates of water content near the edges of the advancing plume exceed 15 % vol vol⁻¹ (Fig. 4b, c), though the general patterns in wetting are consistent. After irrigation, the tomography results on the edges of the wetted zone are in better agreement with the soil moisture probe data, but less spatial information is available given the lack of a wetting front reflection (Fig. 4o).

5 Conclusions

Reflection tomography in the post-migrated domain is a viable method for resolving transient soil moisture content in 2-D associated with an infiltration and recovery event in a homogeneous soil. Reflection tomography of numerical data produced water content distributions that were in good agreement with true water content values from the simulations. The tomography was generally able to match the true water content values to within 5 % vol vol⁻¹–10 % vol vol⁻¹. However, distinct migration artifacts were produced around the edges of the wetting front, especially for cases where the initial water content was non-uniform, obscuring details about the shape of the wetted region. Analysis of data collected in a sand tank proved to be more difficult; however, the tomography was able to produce hydrologically realistic distributions of water content in space and time that were generally within 5 % vol vol⁻¹–15 % vol vol⁻¹ of measurements from in situ soil moisture probes. These discrepancies may have to do with reduction in available reflections for analysis caused by the heterogeneous flow response compared to the coherent wetting front reflection seen in the numerical experiment, e.g., the complex distribution of the wetted soil as a result of heterogenous distribution of water at the surface, texture variability in the soil, or other preferential flow mechanisms (Jarvis et al., 2016). The distance between the location of the CMPs and the moisture probes and the difference in measurement scale between the two methods may also be a source of these discrepancies given the evidence of non-uniform flow. Regardless, the fact that the GPR data were able to capture this heterogeneity is an impressive feat given that tomographic imaging operated independently of any hydrologic information and provided evidence that our conceptual model was not representative of the physical system.

Regardless of discrepancies observed between the GPR and probe water content values, it is evident that automated high-speed GPR data acquisition coupled with reflection tomography algorithms can provide a new approach to hydrologic monitoring. Testing and revision of conceptual hydrologic models regarding non-uniform flow in the vadose zone demands such non-invasive time-lapse imaging data. Artifacts observed in the numerical simulation results, however, suggest that improvements in this methodology could be achieved. While there are likely fundamental limitations to the information content of the data, the Kirchhoff pre-stack depth migration algorithm used in this study could be replaced by more sophisticated algorithms like reverse-time migration (Baysal et al., 1983) which may reduce the observed imaging artifacts. Additionally, results from the tomography algorithm may prove to be beneficial as a precursor to higher-order inversion techniques, like full-waveform inversion, which requires detailed starting models of velocity for convergence. Overall, coupling automated GPR data collection with reflection tomography provides a new method for informing models of subsurface hydrologic processes and a new method for determining transient 2-D soil moisture distributions.