Intra-catchment variability of surface saturation – insights from physically based simulations in comparison with biweekly thermal infrared image observations

In this study, we explored the spatio-temporal variability of surface saturation within a forested headwater catchment using a combined simulation–observation approach. We simulated the occurrence of surface saturation in the Weierbach catchment (Luxembourg) with the physically based model HydroGeoSphere. We confronted the simulation with thermal infrared images that we acquired during a 2-year mapping campaign for seven distinct riparian areas with weekly to biweekly recurrence frequency. Observations and simulations showed similar saturation dynamics across the catchment. The observed and simulated relation of surface saturation to catchment discharge resembled a power law relationship for all investigated riparian areas but varied to a similar extent, as previously observed between catchments of different morphological and topographical characteristics. The observed spatial patterns and frequencies of surface saturation varied between and within the investigated areas and the model reproduced these spatial variations well. The good performance of the simulation suggested that surface saturation in the Weierbach catchment is largely controlled by exfiltration of groundwater into local topographic depressions. However, the simulated surface saturation contracted faster than observed, the simulated saturation dynamics were less variable between the investigated areas than observed, and the match of simulated and observed saturation patterns was not equally good in all investigated riparian areas. These mismatches between observations and simulation highlight that the intra-catchment variability of surface saturation must also result from factors that were not considered in the model set-up, such as differing subsurface structures or a differing persistence of surface saturation due to local morphological features like perennial springs.

1 Introduction

It is critical for flood risk assessment to understand where and when water is standing or flowing on the ground surface outside of perennial surface water bodies. In general, such saturated surface areas arise from (1) water ponding on the surface due to precipitation intensity exceeding the infiltration capacity of unsaturated soil, (2) water ponding on impermeable surfaces or saturated soil, (3) water exfiltrating from the subsurface, or (4) stream water flowing into the floodplain (e.g. Megahan and King, 1985). When saturated surface areas connect to the stream via overland flow, they also become crucial for runoff generation and water quality. While overland flow from saturated surface areas was considered the dominant runoff generation process in early years of catchment hydrology (e.g. Betson, 1964), surface runoff is nowadays known to only dominate in specific environments such as urban areas and Mediterranean or arid catchments (e.g. Latron and Gallart, 2007). Nonetheless, surface saturation and overland flow also occur in forested, humid temperate catchments and other environments where runoff generation is dominated by subsurface flow processes, mainly – but not exclusively – due to saturation excess in the vicinity of the stream (cf. variable source area concept, e.g. Dunne et al., 1975; Hewlett and Hibbert, 1967; Megahan and King, 1985). Such an occurrence of surface saturation and overland flow in the riparian zone can mediate a fast connection between the hillslopes and the stream, inducing quick responses of streamflow to rainfall events and influencing the mixing of different water sources and water quality in the stream (cf. e.g. Ambroise, 2004; Birkel et al., 2010; Bracken and Croke, 2007; Tetzlaff et al., 2007; Weill et al., 2013).

Over the past years and decades, various field studies have mapped and analysed the spatial and temporal occurrence of surface saturation within different landscapes (e.g. Ambroise, 1986, 2016; Dunne et al., 1975; Gburek and Sharpley, 1998; Latron and Gallart, 2007; Silasari et al., 2017; Tanaka et al., 1988). From these field studies it is well recognised that surface saturation varies in space and time and that this variability is affected by structural (e.g. topography) and dynamic factors (e.g. precipitation intensity, antecedent moisture). Yet there is limited understanding on how surface saturation evolves spatially and temporally between and within landscapes and how the interplay of different controlling factors and processes affects the spatio-temporal variability of surface saturation.

Spatially distributed and dynamic hydrological models are potential tools for analysing the generation and development of surface saturation in space and time. While a model is always a simplified representation of reality, the large asset of spatially distributed and dynamic hydrological models is that they allow detailed investigation of surface saturation at any desired location and time. This goes far beyond the information that can be gained by field observations. Several simulation studies have systematically assessed the influence of static and dynamic factors on the temporal evolution, connectivity, and spatial distribution of surface saturation by performing virtual experiments with hillslope models (Ogden and Watts, 2000; Reaney et al., 2014) or by testing a range of terrain indices for predicting time-integrated saturation patterns (Güntner et al., 2004). Other studies relied on dynamic distributed and semi-distributed simulations for analysing the connectivity of surface saturation in relation to wetness conditions and catchment runoff (Mengistu and Spence, 2016; Qu and Duffy, 2007; Weill et al., 2013). Weill et al. (2013) and Partington et al. (2013) analysed the processes and water sources that generate surface saturation in a wetland and a pre-alpine grassland headwater, respectively. Both studies applied an integrated surface–subsurface hydrologic model (ISSHM; Sebben et al., 2013), which can simulate the interplay of different surface and subsurface processes leading to surface saturation (e.g. ponding of precipitation from the surface, exfiltration from the subsurface). However, modelling studies that focus on a comprehensive spatio-temporal analysis of surface saturation dynamics within a landscape by evaluating the spatially distributed model outputs rather than the aggregated outputs are scarce (e.g. Nippgen et al., 2015, for saturated subsurface areas).

When complementing field observations with simulations to analyse the generation and development of surface saturation in space and time, it is important to ensure that the model yields realistic results. Glaser et al. (2016) demonstrated for a small riparian area that a good match between modelled and observed discharge or soil moisture does not automatically imply a realistic simulation of saturation patterns. They concluded that a spatial validation of the dynamic saturation patterns itself is crucial. However, only a few of the existing modelling studies explicitly checked the realism of their simulated surface saturation with field observations before using them for further analyses. Moreover, the few existing studies that performed an explicit validation of simulated surface saturation focussed either on temporally integrated spatial patterns (Grabs et al., 2009; Güntner et al., 2004) or on temporal dynamics of overall catchment saturation (Birkel et al., 2010; Mengistu and Spence, 2016), but hardly any study combined the observation and simulation of both surface saturation patterns and dynamics (Ali et al., 2014; Glaser et al., 2016). The lack of such studies is certainly explainable by the resources that are necessary for obtaining appropriate field data. Today, we still lack a standard method to map surface saturation, and the different existing methods such as the “squishy boot” method, the use of “on–off” surface saturation sensors, the mapping of soil morphology or vegetation as surrogates, and the usage of remote sensing techniques (e.g. Dunne et al., 1975; Gburek and Sharpley, 1998; Güntner et al., 2004; Latron and Gallart, 2007; Mengistu and Spence, 2016; Silasari et al., 2017) all have their own advantages and disadvantages.

A relatively new and powerful method for mapping surface saturation is thermal infrared (TIR) imagery. TIR mapping relies on the difference between the surface temperature of water and other materials to identify surface saturation. Previous work showed that recurrent mapping of surface saturation with high spatial resolution is possible with TIR imagery (Glaser et al., 2016; Pfister et al., 2010). Glaser et al. (2018) and Antonelli et al. (2020) applied TIR imagery mapping in the 42 ha forested Weierbach catchment in western Luxembourg and monitored the dynamics of surface saturation within several distinct riparian areas along the Weierbach stream with a weekly to biweekly mapping frequency over several seasons. While Glaser et al. (2018) focused on method development and image processing, Antonelli et al. (2020) analysed the saturation dynamics in various riparian areas and related them to meteorological and hydrological conditions. They found similar seasonal extension and contraction dynamics of surface saturation between their investigated areas. This was particularly related to near-stream groundwater level fluctuations, yet Antonelli et al. (2020) also identified some local differences of saturation dynamics related to the location and morphological characteristics of the distinct riparian areas.

In this study, we explore the intra-catchment variability of temporal and spatial characteristics of surface saturation (dynamics, frequencies, patterns) based on a combination of field observation and modelling. We perform the study in the Weierbach catchment (42 ha), where we can rely on existing TIR imagery data (Antonelli et al., 2020; Glaser et al., 2018) and on previous modelling work for a 6 ha headwater of the catchment (Glaser et al., 2016, 2019) with the ISSHM HydroGeoSphere. Glaser et al. (2016, 2019) simulated the 6 ha headwater by accounting for layering of the subsurface, while spatial heterogeneity was simplified to topography, including microtopographical features with extents of tens of centimetres to a few metres, and a different sequence of subsurface layers in the riparian zone compared to the hillslopes and plateau area. They set up, adapted, and assessed the simulation based on various distributed field data, including TIR imagery observations of surface saturation in the source area of the stream of the 6 ha headwater (Glaser et al., 2016). Here, we extend the model set-up to the entire 42 ha catchment without introducing additional heterogeneity and without a re-calibration. The expansion of the model to the entire catchment allows the simulation and investigation of the spatial and temporal variability of surface saturation within the catchment, including various distinct riparian areas with a range of morphological characteristics (e.g. extent, location along the stream). Furthermore, this also enables us to study the potential occurrence of different hydrological processes within the different areas that was suggested by the previous analysis of the TIR imagery observations (Antonelli et al., 2020). The temporal focus of our study is on the seasonal dynamics of surface saturation. By contrasting the simulation results with observed surface saturation characteristics from TIR imagery, we use the model as a learning tool and address the following research questions:

1. To what extent can we reproduce the observed intra-catchment variability of surface saturation characteristics with a rather homogenously set up ISSHM?

2. What key controls for the intra-catchment variability of surface saturation characteristics can we identify based on the match and mismatch between simulation results and observations?

The specific surface saturation characteristics that we consider for both questions are as follows:

• i.

  the temporal dynamics of surface saturation extent,

• ii.

  the relationship between surface saturation extent and catchment discharge,

• iii.

  the spatial patterns of surface saturation occurrence, and

• iv.

  the spatial patterns of surface saturation frequencies.

We base our analysis on existing TIR imagery data (Antonelli et al., 2020; Glaser et al., 2018) and perform additional analyses of the field data in order to fully characterise the intra-catchment variability of the temporal dynamics of surface saturation extent and the spatial patterns of surface saturation occurrence and frequency. The analysis includes TIR images taken during different seasons and under differing wetness conditions (25 months with weekly to biweekly mapping resolution) of seven different riparian areas across the Weierbach catchment. The catchment model is based on the previous modelling work for the 6 ha headwater (Glaser et al., 2016, 2019). We first evaluate the 42 ha catchment model against distributed measurements of discharge, soil moisture, and groundwater levels and investigate the catchment-wide simulation of surface saturation patterns and dynamics. Then, we identify the different simulated surface saturation characteristics (i)–(iv) for the seven distinct riparian areas and compare them with the respective field observations to answer the two research questions.

2 Study site and data

2.1 Physiography, climate, and hydrometry

The Weierbach catchment is an intensively studied headwater catchment (42 ha) in western Luxembourg. About half of the catchment area is characterised by gentle slopes < 5^∘, forming a plateau landscape unit (Martínez-Carreras et al., 2016). The rest of the catchment is characterised by hillslopes with slopes > 5^∘, forming a central V-shaped stream valley from north to south and a V-shaped tributary valley in the east. A third stream tributary, which is a few metres long, is situated west of the central stream valley. Riparian zones along the stream account for 1.2 % of the catchment area (Antonelli et al., 2020). Large parts of the catchment are forested with deciduous trees (mainly European beech and sessile oaks); the south-east and some other small parts of the catchment are forested with conifers (mainly Norway spruce and Douglas spruce). The riparian zones are free of trees and covered with ferns, moss, and herbaceous plants. Siltic, sceletic Cambisols, developed from Pleistocene periglacial slope deposits, are shallow and highly permeable, with a depth ranging between 0.4 and 0.9 m (Gourdol et al., 2018; Juilleret et al., 2011; Moragues-Quiroga et al., 2017). Beneath the solum, a 0.5–1 m thick basal layer with bedrock clasts oriented parallel to the slope overlies fractured Devonian slate and phyllites (Gourdol et al., 2018; Juilleret et al., 2011; Moragues-Quiroga et al., 2017; Scaini et al., 2017). In the riparian zones, the Cambisol and the basal layer have been eroded and the fractured bedrock is overlain by shallow organic Leptosols (Glaser et al., 2016).

The climate is oceanic–continental without apparent seasonality in precipitation and with negligible amounts of snow (Carrer et al., 2019). Mean annual precipitation during the period from October 2013 to September 2017 was 955±53 mm. Mean annual discharge was 546±253 mm, with exceptionally dry conditions in the hydrological year 2016–2017. During wet periods, discharge is characterised by double peak hydrographs, with the first peaks appearing immediately in response to precipitation and the second pronounced peaks appearing 48 to 72 h later (cf. Martínez-Carreras et al., 2016). During dry periods, only the first hydrograph peaks occur and the stream dries out intermittently starting from the source areas downstream.

Hydrological and meteorological data that were used in this study were measured from October 2013 to January 2018. Data from the period from October 2013 to September 2015 were used for spin-up simulations, and data from the period from October 2015 to January 2018 were used to drive and validate the actual simulation (cf. Sect. 3). Discharge was measured with water pressure transducers (ISCO 4120 Flow Logger, 15 min logging intervals) at four v-notch weirs, installed at the outlet of the catchment (SW1, Fig. 1) and upstream of the confluences of the three tributaries (SW2–SW4). Groundwater levels were continuously recorded every 15 min with pressure sensors (OTT CTD) in five piezometers installed in different landscape units (riparian zone, hillslope, plateau) of the catchment (Fig. 1, GW1-3, GW5, GW7). Soil moisture was continuously monitored (30 min logging intervals) with water content reflectometers (CS650, Campbell Scientific) installed horizontally at 10, 20, 40, and 60 cm depth at four different sites (Fig. 1, SM3-SM5, SM7). At each site, two depth profiles were monitored. In addition, soil moisture at 10 cm depth was monitored with water content reflectometers (CS616, Campbell Scientific, 30 min logging intervals) at five locations transecting the riparian zone of the stream source area of the middle tributary (Fig. 1, TSM1-TSM5).

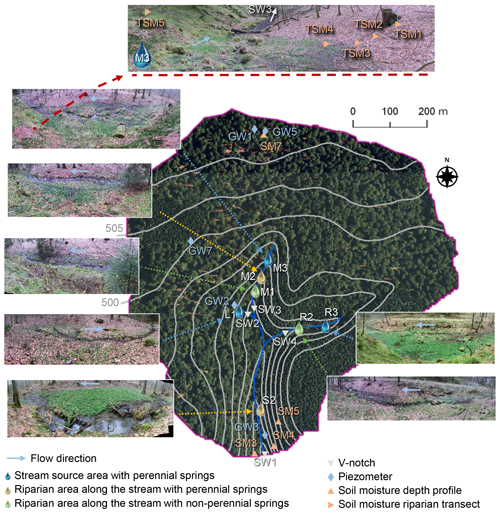
Figure 1 Weierbach catchment with the locations of the installed v-notch weirs for measuring discharge (SW1-SW4), piezometers for measuring groundwater levels (GW1–GW3, GW5, GW7), soil moisture sensors for measuring soil moisture in different depth profiles (SM3-SM5, SM7) and a riparian transect (TSM1-TSM5), and the seven investigated riparian areas along the left (L1), middle (M1–M3), and right (R2, R3) tributary and the central stream (S2). Orthophoto of the catchment: © Administration du Cadastre et de la Topographie 2010 (https://www.geoportail.lu/en, last access: 3 December 2019).

Cumulative precipitation was recorded every 5 min with a tipping bucket rain gauge (Young 52203, unheated, 1 m height) at an open area within the catchment (data gaps were filled based on a linear regression to data from a station approximately 4.5 km southward). Potential reference evapotranspiration was estimated based on measured air temperature, relative humidity, wind speed, and net radiation according to the FAO Penman–Monteith formulation (Allen et al., 1998). Air temperature and relative humidity data were recorded next to the soil moisture profile SM5 (Fig. 1, HMP45C-LC, Campbell Scientific, 15 min logging intervals, 2 m height). Wind speed and radiation data were recorded approximately 4.5 km southward of the study site. Wind speed (Young Wind Monitor 05103, Vector A100R Anemometer) was recorded every 15 min at 3 m height and converted to wind speed at 2 m height (data gaps were filled with data from a station approximately 11.5 km north-eastward) following the FAO guidelines (Allen et al., 1998). Net radiation was recorded every 15 min (Kipp & Zonen NR Lite net radiometer) until May 2017. From June 2017 onward (and for closing other data gaps), we used net radiation data recorded every 5 min close to Luxembourg Airport (∼40 km south-east of the study site), as these measurements were highly correlated (linear regression with an intercept of 7.6 W m⁻² and a slope of 0.92, R²=0.81) with the measurements close to the study site in the years before.

2.2 Surface saturation

Here, we define the surface as saturated as soon as water is standing or flowing on the ground surface (Glaser et al., 2018). This includes water bodies such as ponds and streams, but excludes mere saturation in the topsoil. According to this definition, surface saturation in the Weierbach catchment generally only occurs in the streambed and the adjacent riparian zones. Other areas that were occasionally observed to be surface saturated during very wet conditions or “rain-on-snow” events are forest roads and the extension of the streambed above the source regions into the hillslopes. We focus in this study on seven distinct riparian areas along the left (L1, Fig. 1), middle (M1–M3, Fig. 1), and right (R2, R3, Fig. 1) tributaries, and in the central stream valley (S2, Fig. 1). The seven investigated areas include about one-quarter of the total stream network and areas range from 84 m² for the smallest monitored area (M1) to 232 m² for the largest monitored area (M3) (cf. Antonelli et al., 2020). According to their main hydro-morphological features, the seven areas can be classified into three different categories (Antonelli et al., 2020): (i) stream source areas with perennial springs (L1, M3, R3; blue icons in Fig. 1), (ii) areas along the stream with perennial springs (M2, S2; yellow icons in Fig. 1), and (iii) areas along the stream with non-perennial springs (M1, R2; green icons in Fig. 1).

We mapped the surface saturation in the seven riparian areas weekly to biweekly from November 2015 to December 2017 with thermal infrared imagery. Details on the identification of surface saturation with TIR imagery and on the collected surface saturation dataset are presented and discussed in Glaser et al. (2018) and Antonelli et al. (2020). In brief, we took a panoramic photograph of each of the distinct riparian areas with a handheld TIR camera (FLIR T640) on each mapping day. The TIR panoramas were taken each time from the same position in order to ensure a consistent areal coverage and angle of view. In addition, we manually co-registered the individual panoramas against a reference panorama for each area in an image post-processing step (cf. Glaser et al. 2018). Nonetheless, slight shifts in perspective between the panoramas of different dates were inevitable and the different features (e.g. streambed, stones, trees) in the images did not always overlap exactly pixel by pixel.

The locations of surface saturation (including the stream) were identified from the TIR panoramas based on the acquired temperature information. Each pixel in a TIR panorama was either considered to be saturated or unsaturated based on the temperature range of locations that were obviously saturated according to field observations and visible light images taken complementary to the TIR panoramas. The definition of the temperature range was done manually and individually for each mapping time and location (cf. Antonelli et al., 2020). While this is a subjective and laborious approach, previous sensitivity and uncertainty analyses showed that it is a robust and reliable method, especially if the definition of the temperature range is done by the same person for all the images (cf. Antonelli et al., 2020; Glaser et al., 2018). In case the contrast between water temperature and temperature of surrounding materials was not sufficient for a reliable pixel classification, the images were excluded from the analysis. In case the pixel classification was affected by a poor temperature contrast or by pixels representing vegetation or snow cover, the images were analysed but flagged as less reliable. Altogether, we obtained from 63 monitoring dates a total of 291 binary panoramic images (i.e. 66 % of the 441 panoramas taken) showing the temporal dynamics of surface saturation patterns in the seven studied riparian areas. The total number of analysed binary images per site ranged between 34 (L1) and 48 (M2).

Time series of saturation were created for each area by accounting for the percentage of saturated pixels within the individual panoramic images. We normalised the percentages to the maximum observed percentage of saturation in the distinct areas in order to allow a comparison of the saturation dynamics between the different riparian areas. Moreover, we compared the relationship between the normalised extent of surface saturation and catchment discharge for the different riparian areas with regard to monotonicity (quantified by Kendall correlation coefficients) and shape. In order to visualise the spatial surface saturation patterns and dynamics within a distinct riparian area, we created maps of saturation frequency. We counted for each riparian area how often the individual pixels of the panoramic TIR images were classified as saturated and normalised the resulting frequency numbers by the total number of TIR images analysed for that area. The resulting maps of normalised saturation frequency suggest that very few pixels were always saturated (i.e. reaching a normalised frequency of 1). Field experience and the analysis of individual TIR and visual images showed that in reality, surface saturation was permanent at more places than indicated by the frequency maps. The reason for this artefact is that the perspective and distortion within the individual TIR panoramas was not 100 % identical for all mapping instances (see above) and that vegetation sometimes covered parts of the saturated surface, especially for instances where the extent of surface saturation was small. As a result, the generated saturation frequency maps are blurred. Nonetheless, the maps of normalised saturation frequencies are very useful to quickly detect where surface saturation occurs more or less frequently within an area and for model validation.

3 Catchment model

3.1 Model set-up and parameterisation

We simulated the spatio-temporal dynamics of surface saturation across the Weierbach catchment with HydroGeoSphere (HGS, Aquanty Inc.). HGS is an integrated surface–subsurface hydrological model and allows simultaneous simulation of transient surface and subsurface flow. Subsurface flow is simulated based on the 3D Richards equation. Surface flow is simulated based on the diffusive-wave approximation of the 2D Saint-Venant equation. Evapotranspiration is simulated with a comparatively simple approach, following the mechanistic concept of Kristensen and Jensen (1975). The equations are linearised implicitly using the Newton–Raphson approach and solved in an unstructured finite-element grid. HGS has been used in the past to address diverse questions at various temporal and spatial scales (e.g. Ala-aho et al., 2015; Davison et al., 2018; Erler et al., 2019; Frei et al., 2010; Munz et al., 2017; Nasta et al., 2019; Partington et al., 2013; Schilling et al., 2017; Tang et al., 2018). It was also already applied for a 6 ha headwater region of the Weierbach catchment for simulations within the period October 2010 to August 2014 (Glaser et al., 2016, 2019). The 6 ha headwater model included the source area of the middle tributary and was set up, manually calibrated, and evaluated based on various distributed field data. The evaluation also included a validation of the simulated surface saturation based on 20 TIR images collected in winter 2010–2011 and spring 2014 for the western part of riparian area M3. In this study, we applied the parameterisation of Glaser et al. (2016) to the entire 42 ha catchment without any additional parameter calibration.

The catchment was spatially discretised into 42 274 triangular elements (Fig. 2a), using the mesh generator AlgoMesh (HydroAlgorithmics Pty Ltd). Edge lengths of the mesh elements ranged from > 30 m at the plateau to < 0.4 m for the seven analysed riparian zones and the streambed (Fig. 2a–b). It was crucial to use such a fine mesh resolution in the riparian zone in order to enable spatial detail for the simulated surface saturation patterns comparable to that obtained with the TIR imagery. The topographic information for the mesh nodes was interpolated from a 0.1 m digital elevation model (DEM). The DEM represented the combination of a coarse DEM of the hillslopes and plateau sites that was interpolated from 10 m contour lines of a topographic map and a highly resolved DEM for the stream valleys that was acquired with ground-based lidar (resolution around 5 cm). By merging and interpolating the two DEMs to a resolution of 0.1 m we ensured that most of the microtopographic information of the riparian zone and streambed was maintained in the model mesh. Vertically, the model grid comprised 5 m, divided into 14 layers with element depths ranging from 0.15 m for the top layers to 0.5 m for the bottom layers (Fig. 2c).

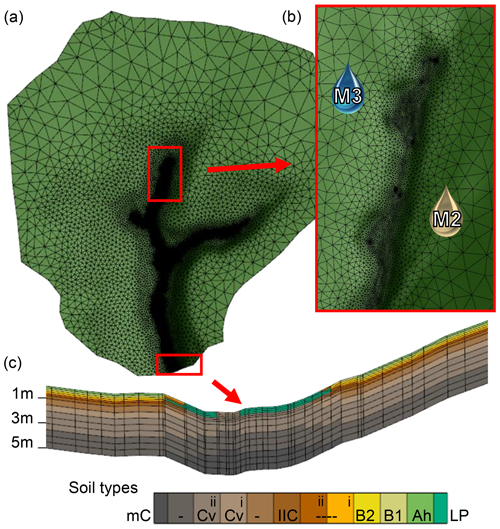
Figure 2 Set-up of the model mesh (a) with a zoom on the fine horizontal resolution in the riparian areas and the streambed (b) and a vertical cross section through the stream valley and adjacent hillslopes (c) showing the vertical discretisation and assignment of different soil properties (cf. Table 1). LP = riparian Leptosol, Ah = topsoil, B1 and B2 = subsoil, IIC = basal layer, Cv = fractured bedrock, mC = fresh bedrock.

Table 1 Soil hydraulic parameters of the different soil property zones. Table adapted from Glaser et al. (2016).

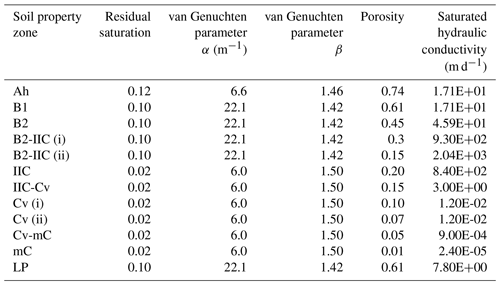
The subsurface was parameterised based on information on the subsurface structure obtained from electrical resistivity tomography (ERT) measurements and a detailed description of soil properties from eight soil profiles distributed across the catchment (cf. Glaser et al. 2016). We parameterised the hillslopes and plateau sites homogeneously with 10 different property layers, representing top- and subsoil (Ah, B1, B2), the basal layer (IIC), fractured and fresh bedrock (Cv, mC), and transition layers between subsoil, basal layer, and fractured bedrock (Fig. 2c). A differing subsurface structure was implemented in the stream valleys because in this area the soil and basal layers are eroded and the outcropping fractured bedrock is overlain with organic, stagnic Leptosol (LP) in the riparian zones (Fig. 2c). We used the Mualem–van Genuchten soil hydraulic functions to describe the saturation–pressure relation. The necessary soil hydraulic parameter values for the different property layers (porosity, residual saturation, van Genuchten α, van Genuchten β, saturated hydraulic conductivity; Table 1) were assigned according to Glaser et al. (2016). They derived the parameter values based on in situ field investigations (ERT profiles) and laboratory measurements. Soil samples were collected for the laboratory measurements from eight soil profiles distributed across the catchment as well as from the shallow soil (5 and 35 cm) of nine locations in the headwater region, including six samples in the hillslope–riparian–stream zone of area M3. Furthermore, Glaser et al. (2016) relied on literature values for the parameterisation of the deeper property layers and performed minor manual value calibration for porosity and saturated hydraulic conductivity against stream discharge measured up- and downstream of area M3 and soil moisture measurements at locations TSM1–5 (cf. Fig. 1). In this study, we added new parameter values for one additional layer for the fractured bedrock (Cv (ii)) in order to account for the adapted depth of 5 m in the catchment model compared to the depth of 3 m in the headwater model.

Surface and subsurface flow were coupled via a Darcy flux exchange through a thin coupling layer (10⁻⁴ m). We assumed different Manning's surface roughness values for the forested area ($\mathrm{1.24}\times {\mathrm{10}}^{-\mathrm{6}}$ d m${}^{-\mathrm{1}/\mathrm{3}}$), the riparian zone ($\mathrm{9.41}\times {\mathrm{10}}^{-\mathrm{7}}$ d m${}^{-\mathrm{1}/\mathrm{3}}$), and the stream bed ($\mathrm{4.4}\times {\mathrm{10}}^{-\mathrm{7}}$ d m${}^{-\mathrm{1}/\mathrm{3}}$) (cf. Glaser et al., 2016). Evapotranspiration parameters (Table S1 in the Supplement) were assigned individually for the deciduous forest, the coniferous forest in the south-east of the catchment, and the riparian zones including the streambed based on the values of Glaser et al. (2016), who assigned the evapotranspiration parameters according to literature values, estimates from field conditions, and calibration against stream discharge and soil moisture measurements. The simulation was driven with daily sums of precipitation and reference evapotranspiration, which were treated as being spatially uniform. The application of the adaptive time-stepping scheme of HGS ensured simulations with sub-daily resolution (minimum time step < 1 min) for periods with highly dynamic hydrologic conditions and coarser temporal resolution (maximum time step 1 d) for less hydrologically active periods. A critical depth boundary was assigned to the outer edge of the surface domain, allowing water to leave the model domain via surface flow. Side and bottom boundaries of the subsurface domain were no-flow boundaries. A spin-up simulation drained the catchment from full saturation to steady-state conditions (for 1 mm d⁻¹ of precipitation, no evapotranspiration) and subsequently repeated the period from October 2013 to October 2015 3 times to obtain realistic initial conditions. The actual simulation spanned the period from October 2015 to January 2018, which is the period where we mapped surface saturation with TIR imagery.

3.2 Assessment of model performance

We evaluated the model performance with discharge, groundwater level, and soil moisture data from various locations within the catchment (Fig. 1). We calculated the Kling–Gupta efficiency (KGE) as a combined measure for correlation, bias, and relative variability (Gupta et al., 2009) between simulated and observed discharge. We also calculated KGEs as combined evaluation criteria for the simulated groundwater levels. Furthermore, we evaluated the simulated groundwater level dynamics rather than absolute values based on Pearson correlation coefficients. Soil moisture was also evaluated based on its dynamics with Pearson correlation coefficients, while absolute values were only compared visually. Since simulated soil moisture was extracted from model nodes whose depths did not exactly correspond with the measurement depths, we interpolated depth-weighted average values from the model output to determine the correlation with the observations in the respective depths. The interpolated model values of volumetric water content were then correlated with the observations of water content, averaging the measurements of the two depth profiles at each monitoring site.

Simulated surface saturation was extracted from the surface domain of the model based on the simulated surface water depths. We classified the cells of the surface domain as saturated if simulated surface water depths were > 10⁻⁴ m, consistent with the definition used to determine surface saturation with the TIR images (i.e. surface saturation is water standing or flowing on the surface; cf. Sect. 2.2.). The depth of 10⁻⁴ m corresponds to the penetration depth for water columns of the TIR camera used and thus is the minimum depth that could be detected based on the pure water temperature signal with the camera. The applied definition of simulated surface saturation in combination with the explicit consideration of a subsurface and surface domain in the HGS model allows differentiation between all water that is standing or flowing on the surface (i.e. surface saturation) and a fully saturated soil surface (i.e. soil water pressure head is zero, but water is not necessarily ponding or flowing on the surface). This implies that the simulated surface saturation can be the result of different processes, i.e. infiltration excess, saturation excess, subsurface water exfiltration, and overland flow. In order to qualitatively assess the importance of saturation excess and groundwater exfiltration in comparison to infiltration excess and overland flow, we compared the simulated frequency of surface saturation with the simulated frequency of groundwater reaching the surface across the entire catchment. The frequency map of surface saturation was generated based on simulated water depths > 10⁻⁴ m in the surface domain at noon on the days where TIR images were taken. Groundwater reaching the surface was identified based on the saturation characteristics of the subsurface domain of the model at noon on the days where TIR images were taken. We marked a cell of the surface domain as a cell where groundwater reached the surface if the subsurface domain below the surface cell was fully saturated from the bottom to the top. This information was then transformed into a frequency map analogous to the procedure for creating the surface saturation frequency maps.

For comparison of the simulation output with the surface saturation information obtained with the TIR images, it was necessary to convert the model output into a comparable format and perspective. First, we transformed the simulated surface water depths for the days with TIR images into binary saturation maps of the entire catchment following the processing described above. Then, we converted the model output into JPEG images with the same perspective and extent as the TIR panoramic images by turning, bending, and cutting the modelled saturation maps according to each of the seven riparian areas individually. This model output processing allowed us to perform the same calculations for the model output as for the TIR images, i.e. to create time series of normalised surface saturation extent, estimate the Kendall correlation for the relationship between normalised surface saturation extent and catchment discharge, and generate maps of normalised saturation frequencies for the seven riparian areas with comparable perspectives and extents. Since it was not possible to project the model output identically to the perspectives of the TIR images, the calculation of quantitative performance metrics for the evaluation of the simulated time series of saturation and simulated frequency maps would have been biased by differences in image distortions and total area extent. Therefore, we evaluated the simulated surface saturation dynamics and patterns qualitatively only by visually comparing the observed and simulated time series of the normalised percentage of saturated pixels and saturation frequency maps generated from the TIR and model images.

4 Results

4.1 Simulation of discharge, groundwater levels, and soil moisture

The model reproduced the seasonal dynamics of measured discharge very well (Fig. 3, Fig. S1). The best fit was obtained at the outlet (SW1) with a KGE of 0.74. Discharge at SW2, SW3, and SW4 was reproduced reasonably well, with KGE values of 0.49, 0.48, and 0.47. Groundwater levels were captured well with the model at the locations close to the riparian zone (KGE =0.57, r=0.78 for GW2; KGE =0.64, r=0.84 for GW3). At hillslopes and plateau sites, simulated groundwater levels were similar to the observed levels during the wet season, but during dry conditions the groundwater levels did not fall deep enough (Figs. 3, S1). This discrepancy was reflected in low KGE values (0.30 for GW1, 0.21 for GW5, 0.02 for GW7). However, the general dynamics of levels increasing and decreasing were also captured at hillslopes and plateau sites (r=0.66 for GW5, r=0.62 for GW7, and r=0.76 for GW1; note that the value for GW1 only includes data for wet periods, since the piezometer dried up during summer months).

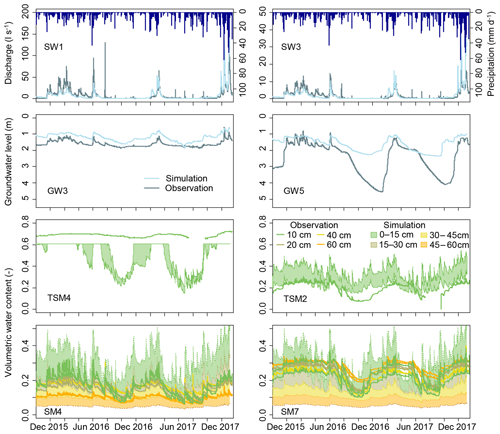
Figure 3 Simulated and observed time series of discharge, groundwater levels below the surface, and volumetric water content. Colour bands indicate the possible span of simulated volumetric water contents in between two model nodes. The time series for the observation locations (cf. Fig. 1) that are not shown here are shown in the Supplement (Fig. S1).

Table 2 Pearson correlation coefficients for the relation between simulated and observed dynamics of volumetric water content of the soil for the different measurement locations and depths (cf. Fig. 1).

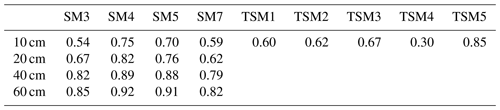
Simulated soil water content generally showed a transition from higher to lower responsiveness from topsoil to subsoil layers, consistent with the monitored soil moisture (Figs. 3, S1). Pearson correlation coefficients indicated overall a good agreement between simulated and observed soil moisture dynamics (Table 2). As for the groundwater levels at the hillslopes and plateau, soil moisture observations showed a distinct decrease in water content during dry periods, which the simulation could not reproduce to the same extent. The observed water content in the riparian zone was always close to saturation, while the simulation showed a decrease in water content during dry periods (TSM4, Fig. 3). Yet the simulation also showed a spatial trend for more permanent soil saturation in the riparian zone (TSM4) and its vicinity (TSM3, Fig. S1) than at the hillslopes and plateau sites. The simulated values of water content were similar to the observed values at some locations (e.g. TSM2, SM4, Fig. 3) and clearly differed at other locations (e.g. SM7, Fig. 3), but the match and mismatch of the volumetric water content did not show any spatial patterns and did not correspond to specific areas or landscape units. Moreover, we think that moisture dynamics and responsiveness are more appropriate for model evaluation than the absolute water content values, since the measured values of volumetric water content also differed within small distances (e.g. measurements of water content in 10 cm depth at profile SM7; Fig. 3).

4.2 Simulated patterns and dynamics of surface saturation versus groundwater reaching the surface at catchment scale

Simulated surface saturation (water depth > 10⁻⁴ m in the surface domain) generally occurred only in the streambed and adjacent riparian zones (Fig. 4a). During the wettest conditions of the study period (winter 2017–2018), surface saturation also extended into the hillslope above the source area R3 of the right tributary (cf. Fig. 1). This simulated occurrence of surface saturation across the catchment is consistent with field evidence, since we observed surface saturation outside of the valley bottom only during very wet conditions or rain-on-snow events (cf. Sect. 2.2). The simulated patterns of where and how frequently groundwater reached the ground surface (full saturation of the subsurface domain, Fig. 4b) were very similar to the simulated surface saturation frequency map of the catchment (Fig. 4a). The only obvious difference occurred in the area above the source area of the right tributary (R3), with a smaller simulated extent of groundwater reaching the surface than the simulated surface saturation extent.

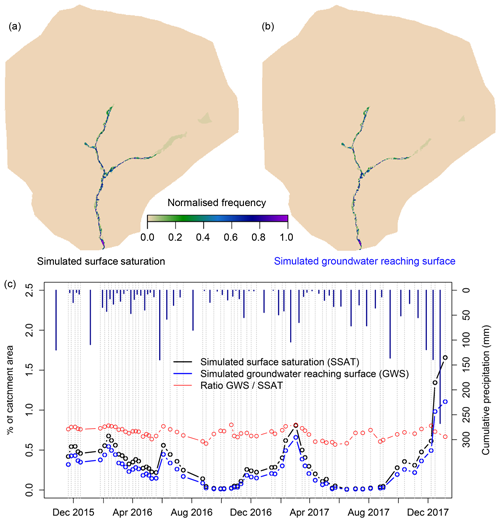
Figure 4 Frequency maps (a, b) and time series of areal percentage (c) of simulated surface saturation and simulated groundwater reaching the surface in the Weierbach catchment. Surface saturation (a, black line in c) corresponds to a simulated water depth > 10⁻⁴ m in the surface domain of the model. Groundwater reaching the surface (b, blue line in c) corresponds to a complete saturation of the subsurface domain of the model, independent of the wetness state of the surface domain. Precipitation is given as cumulative amounts between the observation dates (grey dashed lines).

The time series of simulated percentage of catchment area with surface saturation and groundwater levels reaching the surface revealed that the area where groundwater reached the surface was always smaller in extent than the surface-saturated area, even after dry conditions (Fig. 4c). The biggest absolute difference between the areal extent of surface saturation and groundwater reaching the surface was simulated during winter 2017–2018 (1.7 % vs. 1.1 % of catchment area), when the conditions were very wet with high discharge and high cumulative precipitation. At this time, the difference in areal extent was also visible in the frequency maps (Fig. 4a and b). However, the ratio between the extent of groundwater reaching the surface and the extent of surface saturation was not exceptionally high during winter 2017–2018. Instead, the ratio varied without a clear trend between 0.57 and 0.82 during the entire simulation period, apparently independent from the cumulative amount of precipitation or surface saturation.

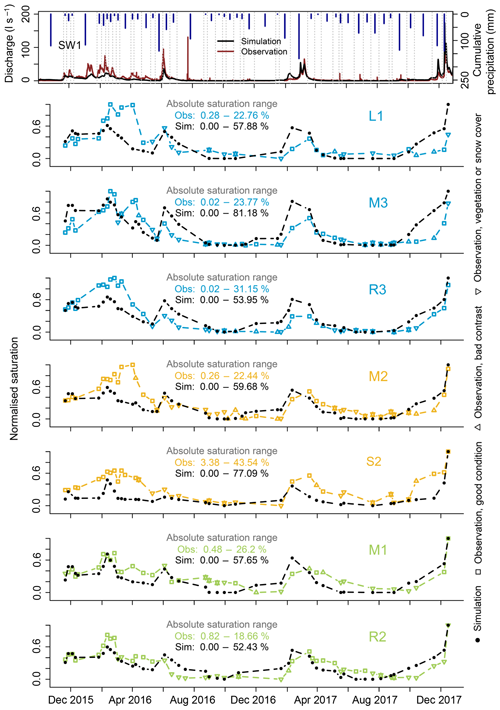
Figure 5 Time series of observed and simulated surface saturation in the seven investigated riparian areas along the left (L1), middle (M1–M3), and right (R2, R3) tributary and the central stream (S2). Colours correspond to the colours of the icons in Fig. 1 and represent the different categories of riparian areas. Surface saturation is normalised to the minimum and maximum amount of saturation that was observed and simulated in the individual areas, respectively. Observations that were derived from TIR images with a poor temperature contrast or with influences of vegetation and snow cover are deemed less reliable and are indicated with triangles (see symbol legend displayed on the right). Cumulative precipitation between the measurement dates (grey dashed lines) and discharge at the catchment outlet SW1 are shown in the top panel to facilitate the comparison to precipitation and flow conditions.

4.3 Temporal dynamics of surface saturation extent within distinct riparian areas

The time series of observed normalised surface saturation extent (Fig. 5, coloured lines) were similar for all seven investigated riparian areas and followed the same seasonal trend as discharge. Yet some differences between the studied areas were discernible. For example, saturation was less persistent between February and April 2016 in the two areas without perennial springs (M1, R2, Fig. 5) than in the other areas. Maximum saturation was reached in December 2017 at M1, R2, and S2, but between February and April 2016 at the other locations (Fig. 5). Similar to the observations, the simulated dynamics of normalised surface saturation (Fig. 5, black lines) followed the trend of the simulated discharge dynamic. The simulation showed a faster decrease and increase in the normalised saturation during dry periods compared to what was observed in most areas. However, simulated discharge also seemed to decrease and increase earlier than the observed discharge (cf. Sect. 4.4). The simulated saturation dynamics did not clearly differ between the different locations and thus were more synchronous than the observations (e.g. maximum simulated saturation in December 2017 in all areas). As a result, the match between simulated and observed dynamics of normalised saturation was better for some areas (e.g. M1, R2, Fig. 5) than for others (e.g. S2, L1, Fig. 5).

The temporal changes of simulated normalised saturation generally matched the observations well, despite under- and overestimation of the minimum and maximum absolute saturation for all areas. The minimum number of saturated pixels in the TIR panoramas ranged between 0.02 % at M3 and R3 and 3.38 % at S2, while the model did not simulate any surface saturation during the driest period (Fig. 5). In addition, simulated normalised saturation remained close to the minimum longer than observed for several areas (L1, S2, M1). These results show that the model simulated a stronger dry-out than observed in the Weierbach. At the same time, the simulation overestimated maximum saturation in the riparian zone (Fig. 5). The overestimation was not the same for the seven investigated areas, and as a result the distinction between areas with higher or lower maximum saturation was not the same for the observations and simulations (e.g. for R3 the second highest maximum saturation was observed compared to the other areas, but the second lowest maximum saturation was simulated).

4.4 Relationship between surface saturation extent and catchment discharge for distinct riparian areas

Kendall correlation between normalised surface saturation and discharge at the outlet (SW1) was > 0.60 for both the observed and simulated for all riparian areas, indicating a monotonic relationship between the weekly to biweekly variation of surface saturation and discharge in all areas (Fig. 6). The simulated relationships between normalised surface saturation and catchment discharge resembled the observed relationships in terms of range and shape (Figs. 6, S2), although the observation data were distinctly more scattered than the simulation data. A power law relationship approximated the observed relationship between discharge and saturation for all seven areas (exponents ranging between 0.29 and 0.69), when data that were taken during rainfall or rising discharge were excluded (cf. Antonelli et al., 2020). For some areas, the simulation matched the trend lines of the observation data closely (e.g. L1, M2). For other areas, the visual fit of the model output to the observations was not as good (e.g. S2, R3) but still described a similar trend.

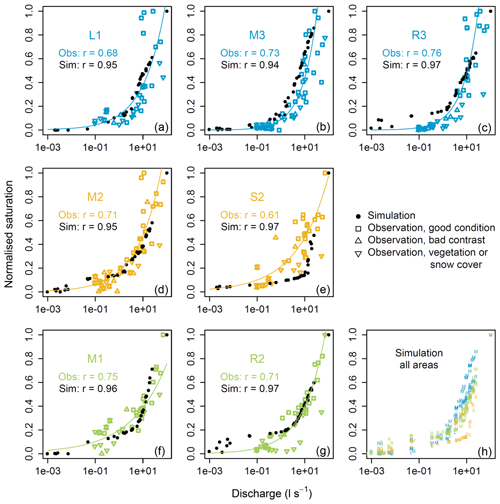
Figure 6 Observed and simulated relationships and Kendall correlations between normalised surface saturation and discharge at the catchment outlet SW1 for the seven investigated riparian areas along (a) left (L1), (b, d, f) middle (M1–M3), and (c, g) right (R2, R3) tributary and (e) the central stream (S2). Colours correspond to the colours of the icons in Fig. 1 and represent the different categories of riparian areas. Observations that were derived from TIR images with a poor temperature contrast or with influences of vegetation and snow cover are deemed less reliable and are indicated with triangles. Simulated data points correspond to the times of observations (cf. Fig. 5); the plotted amount of data points with low and high discharge values differs between the observations and simulations due to mismatches between observed and simulated discharge at these times (cf. Fig. 5). Solid lines are power law curves fitted to the observation data, excluding data taken during rainfall or rising discharge. Note that discharge is plotted in a logarithmic scale, showing relationships of convex shapes although power law exponents are < 1 for all areas. See Fig. S2 for plots with non-logarithmic abscissae and ordinates. To facilitate the comparison between the seven areas, the (h) simulated data points from all seven areas are shown with the different colours and letters of the respective areas in the panel on the bottom right.

Despite the common shape of a power law function, the saturation–discharge relationships were slightly different between the different areas, for both observation and simulation data. For example, the power law functions fitted to the observations indicated that saturation during high-flow conditions (> 5 L s⁻¹) increased most strongly with discharge in the sources areas (especially M3 and R3). During low-flow conditions (< 1 L s⁻¹), the normalised saturation and its change relative to discharge was smallest in the source areas (L1, M3, R3). In the simulated relationships, the increase in saturation for high discharge (> 5 L s⁻¹) was largest for M3 and S2. The simulated relationship between discharge and surface saturation during low flow (< 1 L s⁻¹) was similar for all areas in terms of slope but differed in the extent of normalised saturation, being highest for areas in the right tributary (R2, R3), followed by the areas in the middle tributary (M1, M2, M3) and L1 and S2.

4.5 Spatial patterns of surface saturation: occurrence and frequency within distinct riparian areas

The realism of the simulated patterns of surface saturation was evaluated for each riparian area by visually comparing the surface saturation frequency maps for the simulations and observations (Fig. 7). The model captured the location of the stream and the locations that intermittently became surface saturated well for most of the seven investigated areas. For example, both observations and simulations showed that only the right side of the stream became saturated in M1, that the riparian zone of the right streamside in M2 became saturated only in the upstream part, and that saturation mainly developed on the left streamside in R3, surrounding some permanently dry areas next to the stream (Fig. 7). The only area with a clear mismatch between observed and simulated patterns of surface saturation was area L1, where surface saturation was simulated on the opposite streamside and at a clearly wrong position along the stream (upstream vs. downstream).

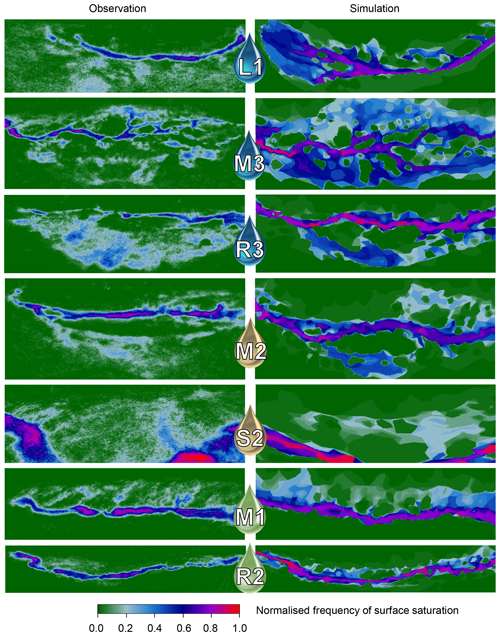
Figure 7 Observed (a) and simulated (b) frequencies of surface saturation in the seven investigated riparian areas along the left (L1), middle (M1–M3), and right (R2, R3) tributary, and the central stream (S2) (cf. Fig. 1). The maps were created by first counting how often the individual pixels were classified as saturated in the individual panoramic images and then normalising the resulting frequency numbers by the total number of images analysed for the respective area.

The simulated surface saturation patterns also reflected the observed saturation frequencies well. The simulation reproduced the general picture of more frequent surface saturation in the streambed than at the streamsides, but – as for the saturation patterns – simulated and observed frequencies corresponded better in some areas (e.g. S2, Fig. 7) than in others (e.g. R3, Fig. 7). For example, the observed frequency of surface saturation in the streambed was generally lower in the source areas (L1, M3, R3) than in the mid- and downstream areas (M2, S2, M1, R2), while the simulated frequency of surface saturation in the streambed was more similar between the areas and particularly overestimated in L1 and R3.

5 Discussion

The aim of this study was to use an ISSHM as a complementary tool to field observations to analyse the spatio-temporal variability of surface saturation in the Weierbach catchment, with a focus on the stream valleys and riparian zones. We found some discrepancies between observed and simulated discharge, groundwater levels, and soil moisture in terms of absolute values. Particularly, the model had some problems to reproduce soil moisture and groundwater levels during the dry conditions at the hillslopes and plateau sites. We nonetheless argue that the match between the observed and simulated time series of discharge, groundwater levels, and soil moisture at different locations was quite good for a model that was not explicitly calibrated against the different time series distributed across the catchment but was set up with uniform parameters. Moreover, the simulated time series of soil moisture and groundwater levels matched the observations especially well in the riparian zone and its vicinity. This gives us confidence that the model set-up was valid for evaluating and analysing the spatio-temporal dynamics of surface saturation and the intra-catchment variability in surface saturation.

5.1 Temporal dynamics of surface saturation extent

The model reproduced the observed dynamics of surface saturation in the seven investigated riparian areas over different seasons and wetness conditions well. Our work goes beyond previous studies that compared the simulation of surface saturation dynamics with observations (e.g. Ali et al., 2014; Birkel et al., 2010; Glaser et al., 2016; Mengistu and Spence, 2016) by relying on a longer study period and a larger number of observations in time. This allowed us to analyse and compare various hydrological conditions and the dynamic transition between them over all seasons with a large number of observations. Moreover, we accounted for spatial variability of saturated area dynamics within the catchment. Unlike the various quasi-dynamic wetness indices presented in Ali et al. (2014), which could not satisfyingly reproduce the spatio-temporal variability of connected saturated surface areas observed in a catchment in the Scottish Highlands, our model reproduced the distributed dynamics of surface saturation well, without clear differences in performance for different wetness conditions.

Simulations and observations both showed that the temporal dynamics of the extent of surface saturation were mostly consistent across the seven different riparian sites of the catchment. Moreover, our simulations showed that the spatio-temporal development of surface saturation was very similar to the spatio-temporal dynamics of groundwater reaching the surface (cf. Fig. 4). This suggests that surface saturation in the Weierbach catchment is largely driven by exfiltration of groundwater into the stream valley and topographic depressions. Note that the high hydraulic conductivities of the upper soil layers that we implemented in the model (cf. Table 1) already implied that surface saturation due to infiltration excess was unlikely to be simulated. This model parameterisation was chosen based on field observations and the previous simulation of the 6 ha headwater around area M3 (cf. Sect. 3.1, Glaser et al., 2016). In addition, the parameterisation is consistent with the common assumption that surface saturation in forested catchments is mainly generated by saturation excess rather than infiltration excess (cf. e.g. Dunne et al., 1975; Hewlett and Hibbert, 1967; Latron and Gallart, 2007; Megahan and King, 1985; Weill et al., 2013). This assumption also proved to be valid for the Weierbach catchment, since the simulations with the chosen parameterisation captured the dynamics of surface saturation extent observed across the catchment. The simulation results furthermore helped to specify that surface saturation in the Weierbach is not the result of saturation excess on any (perched) saturated soil, but is in large parts controlled by a synchronous fluctuation of the groundwater levels across the catchment. Antonelli et al. (2020) drew conclusions that are consistent with our simulation results based on a statistical analysis of the observation data. They analysed the relation between the observed surface saturation dynamics and various hydrometric measurements (i.e. discharge, groundwater levels, soil moisture, field-data-based estimates of catchment storage, precipitation, evapotranspiration) and found that the observed dynamics of surface saturation extent were particularly well correlated to the measured near-stream groundwater level fluctuations. This demonstrates that the simulation could confirm the assumed important role of groundwater exfiltration for surface saturation generation in the Weierbach catchment. We think that future applications of a combined observation and ISSHM simulation approach in other catchments will help to prove whether the identified dominance of groundwater level dynamics in generating saturated soils and subsequent saturation excess surface saturation in the Weierbach is valid for catchments with similar and differing environmental conditions and characteristics.

5.2 Relationship between surface saturation extent and catchment discharge

We found that the observed and simulated relationships between surface saturation and catchment discharge resembled a power law relationship for all areas (cf. Fig. 6). This is consistent with earlier studies that showed power law relationships between contiguous connected saturated surface areas and discharge for events of daily to seasonal timescales (Mengistu and Spence, 2016; Weill et al., 2013). In contrast to these studies that analysed hourly to daily simulation data, we did not observe clear hysteretic loops in the seasonal relationship between saturation and streamflow with our weekly to biweekly data base. The scatter in the observed discharge–surface saturation relationships might indicate that the development of surface saturation in the Weierbach catchment follows hysteretic loops, but that the hysteresis was not resolved with the available temporal resolution of the observations. For example, it is possible that surface saturation evolved in the riparian areas during high-flow conditions and persisted during decreasing streamflow due to restricted infiltration capacities of the riparian soil (cf. Antonelli et al., 2020; Dunne et al., 1975). The HGS model set up for this study might be used in the future to further analyse a possible hysteretic behaviour at the timescale of events. However, there are indications from the weekly to biweekly data that the simulation is currently not able to reproduce possible hysteretic behaviour: (i) the scatter in the simulated discharge–surface saturation relationships identified at seasonal timescale was distinctly lower than in the observed relationships and (ii) the model had a tendency for less persistent and faster contracting surface saturation than observed.

Assuming that the scatter in the observed discharge–surface saturation relationships results from hysteretic extension and contraction of surface saturation, a lack of representation of this phenomenon in the simulation may explain why the simulated saturation dynamics differed less between the different investigated areas than the observed dynamics. It is likely that the observed saturation dynamics were not synchronous between the different areas due to a less persistent generation (and thus less hysteretic behaviour) of surface saturation in the relatively narrow riparian areas without perennial springs (M1 and R2) compared to the wider riparian areas with perennial springs (cf. observation of less persistent saturation in M1 and R2 during February and April 2016, Fig. 5). The model, instead, simulated a non-hysteretic saturation behaviour for all investigated riparian areas, which resulted in a better fit between simulated and observed dynamics in the areas M1 and R2 compared to the other areas. At the same time, it might also be that the simulated relationship between saturation and discharge was correct in all riparian areas and that the scatter of the observations did not result from hysteretic behaviour, but from uncertainties in the TIR methodology. A good argument for a correct simulation of the discharge–surface saturation relationship is that not only simulated saturation but also simulated discharge seemed to be less persistent and to decrease and increase earlier than it was observed. In reality, the scatter of the observation data is likely related to both measurement uncertainties and hysteretic aspects and a future study with higher temporal resolution of field observations and corresponding simulation output could further analyse this.

Independently from the question on hysteretic loops, we found that the discharge–surface saturation relationships somewhat differed between the different areas. We could connect the main differences to different topographical and morphological features, yet we cannot decipher why the main controlling feature for the discharge–surface saturation relationship was different between observations (source areas vs. non-source areas) and simulations (different tributaries; cf. Sect. 4.4). Nonetheless, our findings are in line with experimental studies that showed that the relationships between baseflow discharge and total extent of contributing saturated areas differ between catchments with different physiographic characteristics (e.g. Dunne et al., 1975; Latron and Gallart, 2007).

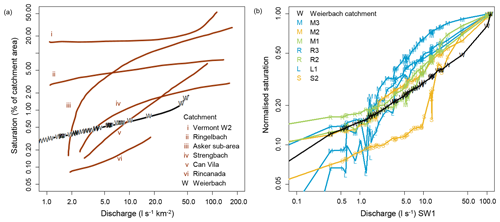
Figure 8 Simulated relationship between discharge and surface saturation of the entire Weierbach catchment (marked with W) in comparison to (a) the relationships observed in other catchments (figure modified from Latron and Gallart, 2007) and (b) the relationships simulated for the seven investigated riparian areas within the catchment (cf. Fig. 6). The data for the relationships from the other catchments are from (i) Dunne et al. (1975), (ii) Ambroise (1986), (iii) Myrabø (Myrabø, 1986), (iv) Latron (Latron, 1990), (v) Latron and Gallart (2007), and (vi) Martínez Fernández et al. (2005).

The variability of shapes of the discharge–surface saturation relationships for the different studied riparian areas within the Weierbach catchment is comparable to the variability of shapes of the discharge–surface saturation relationships for different catchments summarised by Latron and Gallart (2007) (Fig. 8). We cannot compare our results directly with the results shown in Latron and Gallart (2007), since we evaluated absolute discharge and normalised saturation, while they evaluated connected saturated areas in percentage of catchment area but normalised discharge. In order to facilitate the comparison and to connect the two plots (Fig. 8a, b), we show the simulated relationship between discharge and surface saturation of the entire Weierbach catchment in both plots, once with normalised discharge and absolute saturation (Fig. 8a), and once with absolute discharge and normalised saturation (Fig. 8b). The shape of the relationship for the entire Weierbach catchment was nearly linear in double-logarithmic space, similar to the relationship observed in the Can Vila catchment investigated by Latron and Gallart (2007) (Fig. 8a). The relationships of the seven studied riparian areas in the Weierbach differed from the catchment relationship and between each other (Fig. 8b). For example, for area S2 and M1 the shape of the relation in double-logarithmic space was convex and similar to the observations in the Vermont W2 catchment made by Dunne et al. (1975), for area M3 it was rather concave, similar to the relationships found for a sub-catchment of the Asker basin (Myrabø, 1986) and the Strengbach catchment (Latron, 1990), and for area M2 it was rather linear, similar to the Can Vila catchment studied by Latron and Gallart (2007). This clearly shows that differences in the relationship between surface saturation and discharge do not only occur between different catchments, but that they also occur within a catchment, highlighting intra-catchment variability. Different areas within a catchment can behave hydrologically differently due to their location along the stream and differing morphological features. For example, the stream source areas showed a faster increase in surface saturation extent with increasing catchment discharge at low flow but smaller additional increase with increasing catchment discharge at high flow than the riparian areas further downstream (cf. Fig. 8b). This demonstrates that one relationship for the entire catchment is not sufficient to fully resolve the spatially variable relation between discharge and surface saturation since the catchment is internally structured. The impact of this intra-catchment variability on the inter-catchment comparison of landscape controls on the discharge–surface saturation relationships may be a topic for future research.

5.3 Spatial patterns of surface saturation occurrence

The observed spatial patterns of surface saturation occurrence were reproduced well by the simulations for most of the investigated areas. We attribute the successful simulation of the spatial patterns to microtopography (local topographical features with extents of tens of centimetres to few metres) since (i) microtopography described the main spatial variability between the seven investigated areas in the model set-up and (ii) we observed that small changes in the set-up and resolution of the model mesh in the riparian zones changed some details of the simulated surface saturation patterns (Fig. S3, especially area M2, S2). Therefore, we would like to stress that not only major topographic features of the catchment (e.g. hillslope shape, slope angle, valley width) but also its microtopography need to be considered to identify locations where surface saturation may occur. This may sound trivial and several studies have already pointed out the importance of microtopography for the simulation of different hydrological aspects such as hydraulic heads, hyporheic surface–subsurface water exchange, bank storage and overbank flooding, water quality of shallow groundwater systems, and runoff generation (e.g. Aleina et al., 2015; Frei et al., 2010; Käser et al., 2014; Van der Ploeg et al., 2012; Tang et al., 2018), but still microtopography is not often considered in the simulation of surface saturation patterns.

When microtopography is not resolved in sufficient detail, it is more likely that the simulated surface water extends over a large area instead of being confined to topographic depressions and thus the model overpredicts the extent of surface saturation. In this context it is interesting to note that there are studies that simulated maximum extents of surface saturation up to 80 % of the study area (Qu and Duffy, 2007; Weill et al., 2013), while field observations have only shown maximum extents up to 25 %–50 % of catchment area (Ali et al., 2014; Birkel et al., 2010; Dunne et al., 1975; Mengistu and Spence, 2016) and often suggest maximum extents around 10 % (Ambroise, 2016; Grabs et al., 2009; Güntner et al., 2004; Latron and Gallart, 2007; Tanaka et al., 1988). Microtopography might partly explain this discrepancy, even though the maximum extent of surface saturation certainly also depends on the climatic and physiographic conditions of the catchment and on the timing of the observations (e.g. baseflow conditions vs. storm events). Moreover, the importance of microtopography for simulating surface saturation extent likely depends on catchment size. The two mentioned studies that simulated extremely high saturation extent (Qu and Duffy, 2007; Weill et al., 2013) were for small catchments (< 0.1 km²), whereas studies that analysed the extent of surface saturation without considering microtopography in larger catchments (1–100 km²) often simulated similar or smaller maximum extents of surface saturation than observed (e.g. Ali et al., 2014; Birkel et al., 2010; Grabs et al., 2009; Güntner et al., 2004; Mengistu and Spence, 2016).

In our study, the simulated extent of surface saturation reached a maximum of 1.6 % of the catchment area during the very wet conditions in winter 2017–2018 (cf. Fig. 4c). This simulated maximum extent of surface saturation is small compared to the estimates in other simulation studies but is consistent with the observation that surface saturation commonly only occurs within the riparian zone and streambed (extent of 1.2 %) of the Weierbach catchment. Nonetheless, the realistically simulated small maximum extent of surface saturation for the entire catchment did not prevent the maximum saturation within the individual areas from being overestimated compared to the observations (cf. Fig. 5). Besides the effect of microtopography, there are two other possible explanations for this. First, the largest simulated saturation extent occurred during winter 2017–2018, which is the same period in which the model clearly overestimated discharge. This mismatch could partly explain the overestimation of saturation, assuming that the relationship between discharge and saturation was correctly captured with the model (cf. Sect. 5.2). Second, the overestimation of absolute saturation could result from different perspectives and extensions of model output and TIR images (cf. Sect. 3.2, Fig. 7). The TIR images included parts of the hillslopes around the riparian zones, which were not included to the same extent in the extracted model images. Since the hillslopes normally remained unsaturated, the maximum possible number of saturated pixels in the TIR images was thus lower than in the model images, while the minimum possible extent of saturation was not affected. This could also explain why overestimation of total extent of saturation was different between the different areas.

Despite the importance of microtopography, the model results showed that microtopography alone was not sufficient to capture the spatial patterns of surface saturation occurrence correctly. The simulated patterns of surface saturation clearly did not match the observed patterns equally well in all seven investigated areas (cf. Fig. 7), although the topographical information source and mesh resolution was consistent for the simulated riparian areas. This means that there are additional factors that control the spatial patterns of surface saturation occurrence that were not accounted for in the simulations. Such a factor could for example be the structure of the subsurface, which was treated as being homogeneous between all investigated riparian areas in the simulations. In reality, the subsurface structure may locally differ to some degree, for example in the riparian area of the left tributary (L1), where saturation was simulated at the clearly wrong side along the stream. Further field investigations and simulations will be needed to clarify if a varying subsurface structure is sufficient to correct the current mismatch between observed and simulated patterns of surface saturation or if further aspects, such as differing evapotranspiration rates due to varying vegetation cover or exposure to the sun, have a relevant control on the observed saturation patterns as well.

5.4 Spatial patterns of surface saturation frequencies

The frequency maps of surface saturation (cf. Fig. 7) combine information on how often and where surface saturation occurs. We do not think that the exfiltration of subsurface water into the stream valley and local topographic depressions with extents of tens of centimetres to several metres (cf. Sect. 5.1 and 5.2) can fully explain the spatial variability of saturation frequencies that was observed and simulated satisfactorily within the different riparian areas. Instead, we assume that the differences in saturation frequency were controlled by additional water sources than exfiltrating groundwater, such as stream water from upstream or direct precipitation, and that the contribution of these additional water sources to surface saturation varied in space and time. For example, the lower frequencies of surface saturation observed at the streamsides compared to the streambed and the lower frequencies in the streambed of the source areas (L1, M3, R3) compared to the mid- and downstream areas (M2, S2, M1, R2) might reflect a lower and less frequent contribution of upstream water in these areas. The overestimation of simulated saturation frequencies in the streambed of R3 could thus indicate an overestimated upstream contribution due to simulating the stream extent too far upstream from the source area. Moreover, the fact that the simulated extent of groundwater reaching the surface was never as large as the simulated extent of surface saturation in the catchment (cf. Fig. 4) indicates that at least some locations are not exclusively surface saturated due to groundwater exfiltration. It is for example likely that the infrequently surface-saturated area above the source area of the right tributary (R3) (cf. Sect. 4.2) receives water from additional sources such as overland flow or direct precipitation. Future work should analyse potential water sources and surface saturation generation processes in the Weierbach catchment and beyond with a suitable model framework (Partington et al., 2013; Weill et al., 2013) in order to identify the possible mixture of different water sources of surface saturation (e.g. stream water, exfiltrating subsurface water, ponding precipitation), how sources might vary in space and time, and how this might be reflected in surface saturation frequencies.

6 Summary and conclusions

We explored the intra-catchment variability of surface saturation in the 42 ha Weierbach catchment based on observations and physically based simulations. We showed that the model reproduced the observed variability of the different surface saturation characteristics (dynamics, frequencies, patterns) with great detail, although the model set-up was homogeneous and parameters were adopted without re-calibration from the 6 ha headwater model set up previously by Glaser et al. (2016). Our results demonstrated that a spatially distributed, physically based, integrated hydrological model such as HGS is well-suited for reproducing and analysing the generation and development of surface saturation in space and time, if environmental conditions and characteristics are similar to those of the Weierbach catchment. The use of the model as learning tool complementary to the field observations allowed a better understanding of the controls on surface saturation. Based on the identified match and mismatch between the simulation results and observations, we identified groundwater exfiltration and microtopography as key factors controlling the dynamics and patterns of surface saturation. Yet the model results showed that additional factors are needed to explain the full variability of the different characteristics of surface saturation that were observed between the different areas.

The observed and simulated temporal dynamics of surface saturation extent were similar across the catchment, which we inferred – based on the simulation results – to be largely driven by synchronous groundwater level fluctuations across the catchment. Still, we observed differences between the investigated riparian areas with regard to the seasonal dynamics of saturation extension and contraction and the surface saturation – discharge relationship. These differences likely relate to differing morphological characteristics (width, existence of perennial springs) of the riparian areas that induce more or less persistent surface saturation. The model could not fully reproduce the observed variability in persistence of surface saturation. Nonetheless, our simulation results demonstrated that the relationship between surface saturation and discharge for different riparian areas within a catchment can be as variable in shape, as has been observed between different catchments around the globe with different topographical and morphological conditions. Future research should synthesise inter- and intra-catchment landscape controls on dynamic surface saturation extension and contraction and its relation to runoff generation between and within catchments.

The observed spatial occurrence of surface saturation across and within the seven investigated riparian areas was captured well by the simulations, which we related to a large influence of microtopography on the spatial patterns of surface saturation occurrence. However, the model did not reproduce the spatial patterns of surface saturation occurrence equally well in all seven investigated areas. This suggests that some aspects that were not accounted for in the model set-up, such as a spatial variability of subsurface structure, exhibit additional control on the spatial occurrence of surface saturation. Still, the model could satisfactorily reproduce the observed patterns of surface saturation frequencies for most parts of the different riparian areas. We suggest that the spatially varying frequencies of surface saturation might reflect a locally varying importance of different water sources. For locations where the model could reproduce the observed frequencies, the model may be used in a future study to analyse such a potential mixing of different water sources and their variation in space and time.