the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Energy states of soil water – a thermodynamic perspective on soil water dynamics and storage-controlled streamflow generation in different landscapes
Ralf Loritz
Conrad Jackisch
Martijn Westhoff
Axel Kleidon
Theresa Blume
Sibylle K. Hassler
Hubert H. Savenije
The present study confirms that a thermodynamic perspective on soil water is well suited to distinguishing the typical interplay of gravity and capillarity controls on soil water dynamics in different landscapes. To this end, we express the driving matric and gravity potentials by their energetic counterparts and characterize soil water by its free energy state. The latter is the key to defining a new system characteristic determining the possible range of energy states of soil water, reflecting the joint influences of soil physical properties and height over nearest drainage (HAND) in a stratified manner. As this characteristic defines the possible range of energy states of soil water in the root zone, it also allows an instructive comparison of top soil water dynamics observed in two distinctly different landscapes. This is because the local thermodynamic equilibrium at a given HAND and the related equilibrium storage allow a subdivision of the possible free energy states into two different regimes. Wetting of the soil in local equilibrium implies that free energy of soil water becomes positive, which in turn implies that the soil is in a state of storage excess, while further drying of the soil leads to a negative free energy and a state of storage deficit. We show that during 1 hydrological year the energy states of soil water visit distinctly different parts of their respective energy state spaces. The two study areas compared here exhibit furthermore a threshold-like relation between the observed free energy of soil water in the riparian zone and observed streamflow, while the tipping points coincide with the local equilibrium state of zero free energy. We found that the emergence of a potential energy excess/storage excess in the riparian zone coincides with the onset of storage-controlled direct streamflow generation. While such threshold behaviour is not unusual, it is remarkable that the tipping point is consistent with the underlying theoretical basis.
- Article
(5131 KB) - Full-text XML
- BibTeX
- EndNote
1.1 Motivation
Only a minute amount of global water is stored in the root zone of the soil. Yet this tiny storage compartment crucially controls a variety of processes and ecosystem functions. The root zone soil water stock essentially supplies savannah vegetation (e.g. Tietjen et al., 2009, 2010) and more generally ecosystems during severe droughts (Gao et al., 2014). The soil water content controls infiltration, runoff formation and streamflow generation (Graeff et al., 2009; Zehe et al., 2010), it partly determines habitat quality of earthworms (e.g. Schneider et al., 2018) and it is of key importance for soil respiration and emission of greenhouse gases in mountain rainforests (e.g. Koehler et al., 2012). Soil water dynamics are controlled by the triple of infiltration, moisture retention and water release. These processes are driven by the intermittent rainfall and radiative forcing and controlled by multiple forces arising from capillarity, gravity, root water uptake and possibly osmosis. Steady-state hydraulic equilibrium conditions imply that the driving forces act in a balanced manner. In the simple case of absent vegetation and of a flat topography this force balance corresponds to the well-known hydraulic equilibrium, where the matric potential equals the negative of the gravity potential along the entire soil profile. The corresponding equilibrium soil water content profile, which is straightforward to calculate if depth to groundwater and the soil water retention curve are known, reflects thus a balance between the most prominent influences: the local capillary control and the non-local gravitational control. Although these two controls are sensitive to distinctly different systems properties, these properties are not necessarily independent. The climatological and geological setting constrains the co-development or co-evolution of soils, geomorphology and vegetation (as suggested by e.g. Troch et al., 2015; Sivapalan and Bloschl, 2015; Saco and Moreno-de las Heras, 2013). One might hence wonder whether this constrained co-development created a distinctly typical interplay of capillary and gravitational controls on soil moisture. In the present study we show that this interplay manifests through (a) distinct differences in soil water dynamics among different hydrological landscapes and (b) a thermodynamic perspective on soil water dynamics to discriminate typical differences that cannot be inferred from the usual comparison of soil moisture observations.
1.2 Thermodynamic reasoning in hydrology and related Earth sciences
Thermodynamic reasoning has a long tradition in Earth science, ecology and hydrology, and one of its key advantages is a joint treatment of mass fluxes and the related conversions of energy, including dissipation and entropy production. In geomorphology it dates back to the early work of Leopold and Langbein (1962) on the role of entropy in the evolution of landforms. Howard (1971, cited in Howard, 1990) proposed that angles of river junctions are arranged in such a way that they minimize stream power. Bolt and Frissel (1960) related soil water potentials to Gibbs free energy of soil water (referring to the early pioneers Edlefson and Anderson, 1940) and established a link between soil physics and thermodynamics. In ecology Lotka (1922a, b) proposed that organisms that maximize their energy throughput have an advantage within the evolutionary selection process.
Thermodynamics have gained substantial attention in catchment hydrology since the work of Reggiani et al. (1998) and Kleidon and Schymanski (2008). Reggiani et al. (1998) employed thermodynamic reasoning and volume averaging to derive a model framework of intermediate complexity (Sivapalan, 2018). They introduced the idea of a representative elementary watershed, REW, which can be seen as the least spatial entity for building mesoscale hydrological models. This idea has been picked up and advanced by several follow-up studies dealing with the coding and successful application of REW-based hydrological models (Reggiani et al., 1998, 1999, 2000; Reggiani and Schellekens, 2003; Lee et al., 2005, 2007; Zhang et al., 2006; Tian et al., 2006) or the challenge to derive the necessary closure relations (Zehe et al., 2006; Beven, 2006).
Along a different avenue, Kleidon and Schymanski (2008) discussed the opportunity of using maximum entropy production (MEP, originally proposed by Paltridge, 1979) to predict steady-state, close-to-equilibrium functioning of hydrological systems and to infer model parameters based on thermodynamic optimality. This idea has motivated several efforts to predict the catchment water balance using thermodynamic optimality. For instance, Porada et al. (2011) simulated the water balance of the 35 largest basins on Earth using the SIMBA model and inferred parameters controlling root water uptake by maximizing entropy production. They tested the plausibility of their assessment within the Budyko framework (Budyko, 1958). Zehe et al. (2013) showed that a thermodynamic optimum density of macropores created by worm burrows which maximized dissipation of free energy during recharge events allowed an acceptable uncalibrated prediction of the rainfall–runoff response of a lower mesoscale catchment with a physically based hydrological model. While this finding is at least an interesting incidence, the explanation why the worms should create their burrows in such a way is not straightforward. Hildebrandt et al. (2016) proposed that plants optimize their root water uptake by minimizing the necessary energetic investment through a spatially uniform water abstraction from uniform soils. Along similar lines of thought but at much larger scales Gao et al. (2014) proposed that ecosystems optimize their rooting depth. This is deemed to balance the advantage of vegetation to endure droughts of increasing return periods with the necessary energetic investment to expand their root system to enlarge the water holding capacity.
Kleidon et al. (2013) tested whether the topology of connected river networks can be explained through a maximization of kinetic energy transfer to sediment flows. They showed that the depletion of topographic gradients by sediment transport can be linked to a minimization in frictional dissipation in streamflow networks, which in turn implies a maximization of sediment flows against the topographic gradient and thus of power in the sediment flows. The idea that the topology of river networks reflects an energetic optimum – more precisely a minimum – is in fact much older and was already suggested by Howard (1990) and picked up by Rinaldo et al. (1996) as the concept of minimum energy expenditure. Hergarten et al. (2014) transferred this idea to groundwater systems by analysing preferential flow paths that minimize the total energy dissipation at a given recharge under the constraint of a given total porosity and by verifying those against data sets for spring discharge in the Austrian Alps.
Kleidon et al. (2014) and Renner et al. (2016) tested whether a two-layer energy balance model based on maximum power in combination with Carnot efficiency is suited to predicting the partitioning of net shortwave radiation into longwave outgoing radiation and turbulent fluxes of latent and sensible heat. During convective conditions their predictions were in good accordance with flux tower data at three sites with different land use.
While some of us might find the search for thermodynamic optimality exciting and promising, it is certainly not the Philosopher's stone. Westhoff et al. (2013) found for instance that a conceptual model structure which was in accordance with MEP was not suited to predict the water balance in the HJ Andrews experimental watershed. Thermodynamic optimality should thus be seen as a testable and sometimes helpful constraint, but it should not be mixed with a first principle such as the first and second laws of thermodynamics (Westhoff et al., 2019). And thermodynamic optimality is restricted to explaining system steady-state, close-to-equilibrium functioning. The challenge is however to explain operation of hydrological systems under temporarily variable forcing (Westhoff et al., 2014) and far-from-equilibrium conditions.
In summary we think that there are four general arguments why a thermodynamic perspective on soil water dynamics and hydrology in general has much to offer. Firstly, surface runoff and particularly soil water fluxes dissipate a very large amount of their driving energy differences. As the dissipation and related entropy production rates depend on the soil material and on the spatial organization of the material as well (Zehe et al., 2010), one may quantify feedbacks between morphological/structural changes and hydrological processes within the same current (joule). Secondly, energy is an extensive quantity; as such it is additive when different systems are merged, it grows with increasing system size and changes can be described through a balance. One may hence apply volumetric averaging and upscaling to energy for instance to derive macroscale effective constitutive relations and macroscale equations as shown by de Rooij (2009, 2011). By contrast, the related gravity and matric potentials are intensive state variables and as such not additive in the sense specified above, nor can their changes be balanced. Thirdly, it can be used to define and explain hydrological similarity based on a thermodynamically meaningful combination of catchment characteristics (Zehe et al., 2014; Seibert et al., 2017; Loritz et al., 2018). Last but not least, one may test whether thermodynamic optimality provides, despite the fact that it is controversial, a means to test the recent proposition of Savenije and Hrachowitz (2017), stating that “Ecosystems control the hydrological functioning of the root zone in a way that it continuously optimizes the functions of infiltration, moisture retention and drainage of catchments”.
1.3 Objectives
In the following, we show that the free energy state of soil water is well suited for characterizing distinct differences in soil water dynamics among different landscapes. Based on the free energy state we define a system characteristic called energy state function, which jointly accounts for the capillary and gravitational control of soil water dynamics, using height over the nearest drainage (HAND, Renno et al., 2008; Nobre et al., 2011) as a proxy for the gravity potential. These energy state functions are strongly sensitive to differences in topography and soil water characteristics of the study area and allow an instructive visualization of soil water dynamics in energetic terms. By comparing two different catchments we found that the soil water storage dynamics in both landscapes operate distinctly differently with respect to the local thermodynamic equilibrium state of minimum free energy. More specifically we provide evidence that the local thermodynamic equilibrium state separates two regimes of a storage deficit and storage excess. During a 1-year period the observed energy states of the soil water in the study areas operated distinctly differently with respect to these regimes and visited distinctly different ranges of their corresponding energetic state space. Last but not least, we provide evidence that the state of zero free energy not only separates regimes of a storage deficit and a storage excess, it is furthermore also a theoretically motivated threshold, explaining the onset of storage-controlled runoff generation, saturation excess overland flow or subsurface storm flow in our study areas.
In the following we express the matric and gravity potentials by their energetic counterparts, following largely the work of Bolt and Frissel (1960) and de Rooij (2009), to characterize soil water storage by its free energy state and derive the energy state function.
2.1 Free energy of the soil water
Following the micro approach of Bolt and Frissel (1960) we start our derivation with the Gibbs free energy G (J) of a small soil volume V (m−3) that contains a test body of water with mass M (kg). Assuming isotherm conditions while neglecting osmotic forces and the energy of water adsorption leads to
where g (m s−2) is gravitational acceleration, dz (m) denotes a change in position in the gravity field, Pe (N m−2) is the external pressure, p (N m−2) is the capillary pressure, dp is the local pressure increment, which relates to the capillary pressure difference between water and air, and Vw is the volume of the test water body. Please note that Eq. (1) is not a total differential; this is why classical textbooks of thermodynamics use the symbol δ instead of the “d”, and speak of a variation in pressure or elevation.
In the next step, we express Eq. (1) as a change in volumetric energy density. When recalling (a) that Vw equals the product of V and the soil water content θ (m3 m−3) and (b) that the water mass M equals the product of its density ρ (kg m−3), V and θ, we obtain
The first term on the right-hand side is mechanical work per volume due to external pressure changes (for instance compression), the second term relates to changes in Gibbs free energy density related to capillary pressure changes, while the last term relates to changes in the potential energy of the gravity field. In the following the work term is neglected, as we are interested in those changes in Gibbs free energy which relate to dynamic changes in the stored water amount (focusing on the liquid phase only). As capillary pressure is equal to the product of matric potential ψ (m) times the unit weight of water, Eq. (2) can be reformulated as follows:
While we acknowledge that the first term on the right-hand side is often referred to as matric potential energy (see e.g. Hillel, 2004). We nevertheless think that the adjective potential is misleading and shortly explain why we deviate from established terminology here. Potential energy refers to the position of a test body of mass M in the gravity field and remains invariant when the inner state of the test (soil) body changes, for instance through compression, when exchanging the fluid mass in the pore space with the same mass of a different fluid. The Young–Laplace equation tells us that both operations change the matric potential in soil, either through a compaction of the soil pores and a reduced pore radius r (m) or through the change in surface tension σ (N m−1):
where φ is the wetting angle. As this form of energy depends on the inner structure of the soil and on the chemical properties of the fluid, it partly determines the inner energy of the soil body in a thermodynamic sense, and the more precisely it relates to surface energy. We thus refer to term 1 in Eq. (3) as “capillary binding energy”, consistent with Zehe et al. (2013).
When deriving Eq. (3) with respect to time (and neglecting changes in z), we find that a change in soil water content implies a change in its free energy state:
Note that the potential energy density of soil water (the second term on the right-hand side) increases linearly with increasing soil water content. In contrast, capillary binding energy decreases with increasing soil water content, as the absolute value of the matric potential declines non-linearly with increasing soil water content. The change in capillary energy density with a given change in soil water content is determined by the product of the actual soil water and the slope of the water retention curve. We thus state that the product of the well-known soil hydraulic potential, ψ+z, and the soil water content corresponds to the volumetric density of free energy of soil water per unit weight. The free energy of soil water for a larger volume is the volume integral of the total hydraulic potential times the soil water content over the volume of interest (de Rooij, 2009; Zehe et al., 2013):
The latter reflects both the binding state and the amount of water that is stored in a control volume at a given elevation above groundwater and thus reflects the local retention properties and the topographic setting as well. Note that the change in potential energy of soil water at a given elevation scales linearly with the soil water content. One might thus wonder whether the dominance of the one or the other energy form may at least partly influence whether a system behaves in a linear or non-linear fashion.
2.2 Hydraulic equilibrium, thermodynamic equilibrium and related soil water content
The state of minimum Gibbs free energy corresponds to a state of maximum entropy and thus to thermodynamic equilibrium. With respect to Eq. (3) this is the case when gravity and matric potential are equal in absolute terms in the entire profile of the unsaturated zone:
In hydraulic equilibrium the absolute value of Gibbs free energy of soil water is thus equal to zero. And the related soil water content, which balances capillary and gravitational influences, is straightforwardly calculated by substituting the matric potential in the soil water retention curve with the depth above groundwater, when the latter is known.
where θs (m3 m−3) is the saturated soil water content and S (–) is the relative saturation. This is illustrated in Fig. 1 for the retention curves of three distinctly different soils.
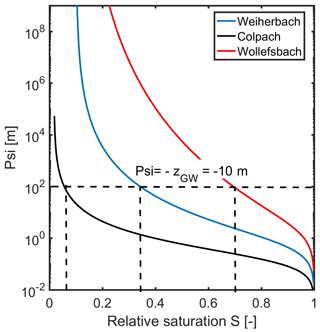
Figure 1Soil water retention curves as a function of relative saturation determined as explained in Sect. 3.1. The dashed black lines mark the relative saturation at hydraulic equilibrium, assuming arbitrarily a depth to groundwater of zGW=10 m. The Wollefsbach and the Colpach are further characterized in Sect. 3; the Weiherbach is used here for purposes of comparison and is briefly described in Sect. 2.2.
Note that the different soils are at the same depth to groundwater, for instance at zGW=10 m in Eq. (7), characterized by very different equilibrium saturation values. The equilibrium saturation of the clay-rich soil in the marl geological setting of the Wollefsbach catchment is at Seq=0.82 rather high, while the young silty soil located in the Colpach has a rather low saturation at equilibrium of Seq=0.13. The loess soil from the Weiherbach is at Seq=0.53 in between these extremes. Note that two of those soils are located in our respective study areas Colpach and Wollefsbach in Luxembourg (compare Sect. 3). We added the Weiherbach soil located in Germany to complete the spectrum of possible endmembers.
2.3 Free energy state as a function of relative saturation
The equilibrium storages shown in Fig. 1 separate ranges of relative saturation where the corresponding free energy of the soil water is either negative or positive. This becomes obvious when plotting the specific free energy per unit volume efree (m) of the soil water content at the same elevation above groundwater as a function of the relative saturation for these soils (Fig. 2).
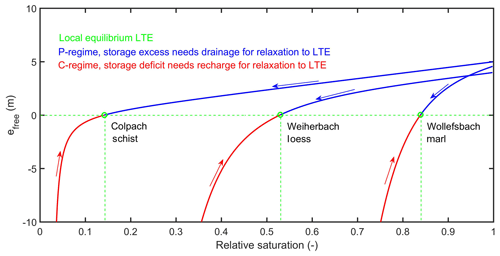
Figure 2Weight-specific free energy state of the soil water storage, as defined in Eq. (8), plotted against the relative saturation of the three different soils, assuming a depth to groundwater of 10 m. The green lines mark the local equilibrium state where the absolute value of the specific free energy is zero and the corresponding equilibrium saturations. Free energy in the P- and C-regimes is plotted in solid blue and red, respectively; the arrows indicate the way back to equilibrium.
Note that efree is, being defined as specific free energy per unit volume, equal to the product of total hydraulic potential and the soil water content. We also assume the soil to be in capillary contact with groundwater (see Sect. 5.2 for further discussion). The horizontal green line in Fig. 2 marks the local equilibrium where the absolute value of the specific free energy at this particular elevation is zero. The vertical lines indicate the corresponding equilibrium saturations at the x axis (corresponding to those in Fig. 1). These equilibrium storages separate the ranges of soil saturation where the corresponding free energy is positive (in blue). This is the case when the potential energy is larger than the capillary binding energy; we call this range the P-regime. In this regime dynamics in soil water content are dominantly driven by differences in potential energy, and gravity dominates. Relaxation back to equilibrium requires the release of water to deplete the excess in potential energy, and the necessary amount is determined by the overshoot of free energy above zero.
Relative saturations smaller than Seq are associated with negative free energy, as the absolute value of the capillary binding energy exceeds potential energy. We call this range the C-regime (in red) because differences in capillary binding energy and thus capillarity act as the dominant driver for soil water dynamics. The system needs to recharge water to restore the “energy deficit” below zero, and the necessary amount depends on the distance to equilibrium. Be aware that particularly small changes in soil water content may, depending on the size of θdψ∕dθ, trigger large changes in free energy.
Figure 2 shows that the three different soils, when arranged at the same geopotential level, are characterized by distinctly different energy state curves as a function of relative saturation. The P-regime is very prominent for the Colpach soil – potential energy dominates over a wide range of saturation, and its efree grows linearly with S for values larger than 0.2. The clay-rich soil of the Wollefsbach has a diametrical pattern, capillarity dominates the energy state for 82 % of the possible saturations and the absolute value of efree grows in a strongly non-linear way with declining saturation. The energy state function of the loess soil (Weiherbach) is in between the other two extremes, with an equilibrium at a saturation of 53 %.
As described in Eq. (8), the energy state functions shown in Fig. 2 depend on the soil water retention curve and the depth above groundwater. While depth to groundwater is usually not exactly known, height over the next drainage (HAND, Renno et al., 2008; Nobre et al., 2011) provides an easy-to-measure surrogate when taking the water level of the closest stream as a reference. While depth to groundwater increases obviously proportionally to HAND, the related proportionality factor c is not straightforward to calculate. For draining rivers, c is less than or equal to 1, the minimum is expected to be of the order of 0.8, and c may increase with increasing distance to the river, reflecting the topography of the groundwater surface. In addition, the proportionality changes dynamically in response to the spatio-temporal pattern of groundwater recharge, the hydraulic properties of the aquifer, the topography of an aquitard, and the water level in the stream. Yet we may characterize the upper limit of free energy states of root zone soil water storages in a stratified manner by a “family” of energy state curves, if we know (a) the retention functions of the soils and (b) the frequency distribution of HAND h(zHAND) in the system of interest.
This family of curves characterizes how HAND and soil physical characteristics jointly control the free energy state of soil water as a function of the relative saturation. The presentation of the energy state functions for our study areas in the following Sect. 3 will reveal that all points in the root zone with the same soil water retention curve and which fall into the same bin of HAND are represented by the same energy state curve.
The derived energy state function introduced in the last section defines the possible energy states of the soil water storage, a thermodynamic state space of the root zone so to say. Due to the intermittent rainfall and radiative forcing, their respective annual cycles, the free energy state of soil water will be pushed and pulled through this state space. It appears thus straightforward to visualize these storage dynamics, either observed or modelled, as pseudo oscillations of the corresponding free energy state in the respective energy state functions. This will teach us (a) which part of the state space is actually visited by the system, and (b) whether the system predominantly operates in one of these regimes or within both of them. In the following, we briefly characterize the study areas and the data set we use for this purpose.
3.1 Study areas
The Colpach and Wollefsbach catchments belong to the Attert experimental basin (Pfister et al., 2002, 2017), and are distinctly different with respect to soils, topography, geology and land use (Fig. 4). Both catchments have been extensively characterized in previous studies with respect to their physiographic characteristics, dominant runoff generation mechanisms and available data (Wrede et al., 2015; Martinez-Carreras et al., 2015; Loritz et al., 2017; Angermann et al., 2017). Hence, we focus here exclusively on those system characteristics which determine their respective energy state functions. The Colpach has an elevation range from 265 to 512 m. Soils are young silty haplic Cambisols that formed on schistose periglacial deposits. Despite their high silt and clay contents they are characterized by a high permeability and high porosity (Jackisch et al., 2017), because the fine silt aggregates embed a fast draining network of coarse inter-aggregate pores. In contrast, the Wollefsbach has a much more gentle topography, from 245 to 306 m a.s.l. Soils in this marl geological setting range from sandy loams to thick clay lenses.
3.2 Storage data, soil water characteristics and energy state functions
For this study, we use data from a distributed network of 45 sensor clusters spread across the entire Attert experimental basin (Fig. 3) collected within the hydrological year 2013/2014. These sensor clusters measure, among other variables, soil moisture and matric potentials within three replicated profiles in 0.1, 0.3 and 0.5 m depths using Decagon 5TE capacitive soil moisture sensors and MPS1 matric potential sensors. In this application we focus on data collected at 0.1 m depth; the distributions of sensors along HAND in the Wollefsbach and the Colpach are shown in Fig. 3b and c, respectively. Note that we use HAND as an estimator for the depth to groundwater here. Soil water retention was in both catchments analysed by Jackisch (2015) using a set of 62 undisturbed soil cores from the Colpach and 25 undisturbed soil cores from the Wollefsbach (Fig. 4a and b).
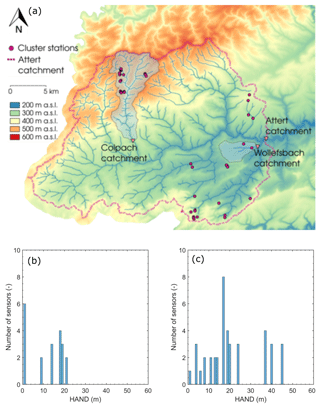
Figure 3Map of the Attert basin with the Colpach and Wollefsbach catchments (a, taken from Loritz et al., 2017). The red dots mark the sensor cluster sites of the CAOS research unit, which collect, besides the standard hydro-meteorological data, soil moisture and the soil water potential. (b) and (c) show the distribution of the sensors with respect to HAND for the Wollefsbach and Colpach, respectively.
Here we do not use these point relations, but representative, macroscale soil water retention functions to derive the energy state function of our study areas (Fig. 4c and d). These were derived by Jackisch (2015) from the raw data of all lab analyses as follows. He pooled the matching pairs of soil water content and matric potential observed in each soil core experiment in the same landscape setting into a single statistical sample (Fig. 5c and d). When using the tension () as an independent variable, we interpret the corresponding soil water contents of the 62 or 25 samples as a conditional random variable. The sample reflects the heterogeneity of the soil and needs to be characterized by a conditional frequency distribution h(θ|ψ). And the latter needs in turn to be characterized by its moments and percentiles. The averaged soil water content at each matric potential/tension-level is an estimator of the expected value of the soil water content at this tension.
We define the representative retention curve as the one that relates the expected soil water storage to the matric potential , and the latter may be obtained by fitting a suitable retention function to the data; we used the van Genuchten model here (Jackisch, 2015). Note that this relation cannot be observed at a single site. It is an effective macroscale retention function characterizing the relation between the expected soil water content in the landscape and the matric potential, reflecting random distribution h(θ|ψ).
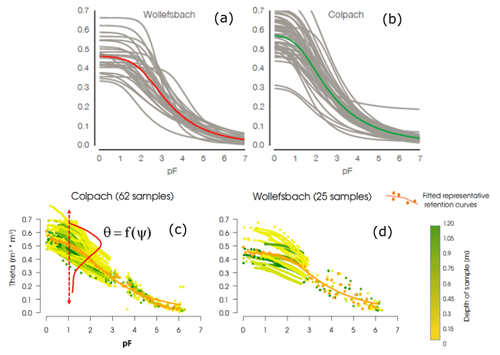
Figure 4(a) and (b) show the retention functions Jackisch (2015) derived from individual soil cores by means of multistep outflow experiments. (c) and (d) illustrate the procedure of pooling the soil water contents observed at a given tension (pF=log 10(ψ)) of all experiments into conditional random samples. The orange points mark the averaged values as a function of the tension and the solid lines are the fitted van Genuchten functions. Note that these representative curves are shown in colour in (a) and (b) as well. The colour code of the individual data points in (c) and (d) relates to the depth of the sample below the surface.
Loritz et al. (2017, 2018) used these effective retention functions for setting up physically based hydrological models for both catchments, which yielded simulations of streamflow and soil moisture dynamics in good accordance with observations. Test simulations with randomly selected retention functions derived from individual soil samples (Fig. 4b) or based on the averages of the van Genuchten parameters of 62 experiments performed clearly worse.
Based on these representative retention functions and the frequency distributions of HAND (Fig. 5b and d), we compiled the energy state functions of both catchments (Fig. 5a and c) according to Eq. (8), using HAND as a surrogate for the depth to groundwater. As stated in the previous section, the energy state function consists of a family of curves, which characterize the free energy state of the soil water as a function of the relative saturation, stratified along the bin centroids of the corresponding frequency distributions of HAND. So each line corresponds to a certain HAND value.
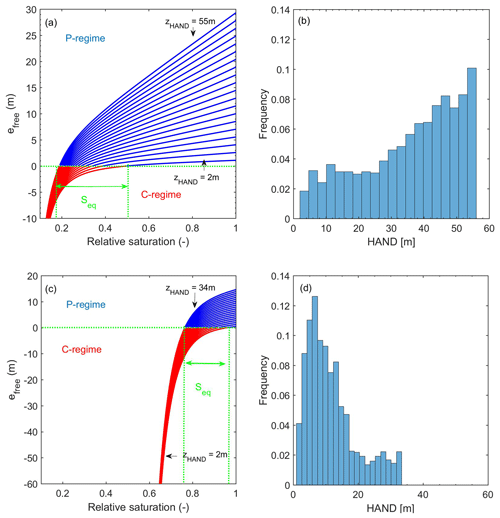
Figure 5Energy state functions of the Colpach (a) and the Wollefsbach (c) derived from the corresponding frequency distribution range of HAND (b and c) and the representative retention functions (note the differences in scales). The horizontal green lines mark the equilibrium of zero free energy, and the vertical green lines mark the corresponding ranges of equilibrium saturations. Please note that efree at a relative saturation of 1 equals the product of HAND and the soil water content at saturation.
Note that the wider HAND range in the Colpach causes a clear dominance of the P-regime over a large saturation range. More importantly, Fig. 5a reveals that for relative saturations larger than ∼0.4 free energy is a multi-linear function of relative saturation. This means that the specific free energy density is at each HAND level a linear function of relative saturation, but the slope of the energy state curves does increase with increasing HAND. The corresponding range of equilibrium saturations is between 0.18 and 0.5. The absolute values of efree are in the corresponding C-regime less than 20 m. In the root zone of the Wollefsbach free energy is by contrast a strongly non-linear function of relative saturation (Fig. 5c). The C-regime is very prominent and efree drops below −100 m for saturations smaller than 0.6. This is mainly due to the high clay content in the soil and to a lesser degree it also reflects the smaller HAND in this landscape. Consistently, we find the range of equilibrium saturations to be between 0.78 and 0.98.
4.1 Soil moisture and its free energy state at two distinct cluster sites
In a first step we inter-compare the free energy states of the soil moisture storage (Fig. 6) which was observed at two arbitrarily selected sites in the respective study catchments. Both sites are located 20 m above their respective streams. The soil water content in the clay-rich top soil of the Wollefsbach site is in the winter and autumn period rather uniform and on average 0.15 m3 m−3 larger than in the Colpach (Fig. 6a), while the soil water content at the Colpach site appears much more variable in these periods. Both sites dry out considerably during the summer period and start to recharge with the beginning of the autumn. Figure 6a shows furthermore that the site in the Colpach operates clearly above the corresponding equilibrium soil water content, θeq=0.139 m3 m−3, while the site in the Wollefsbach drops below its equilibrium soil water content, θeq=0.364 m3 m−3, and operates in the C-regime for almost 3 months.
Figure 6b and c provide the corresponding free energy states of both soil water time series as a function of the soil saturation. Observations are shown as black circles, and the related theoretical energy state curves calculated following Eq. (8) are in blue. The first thing to note is that the observed free energy states for both sites scatter nicely around the theoretical curves. More interestingly one can see that the spreading of the free energy state of the soil water stock is at both sites distinctly different. The free energy state of soil water at the Colpach site is during the entire hydrological year in the P-regime and hence subject to an overshoot in potential energy (Fig. 6b). The site operates in the linear range of the energy state curve and fluctuates around an average weight-specific energy density of 3.2 m, which corresponds to an energy density of 2.9×104 J m−3. While the observations spread across a total range of 3 m (2.9×104 J m−3), their standard deviation is 0.44 m (3.0×103 J m−3). The coefficient of variation of the free energy state of the soil water content is hence at 0.14 rather small.
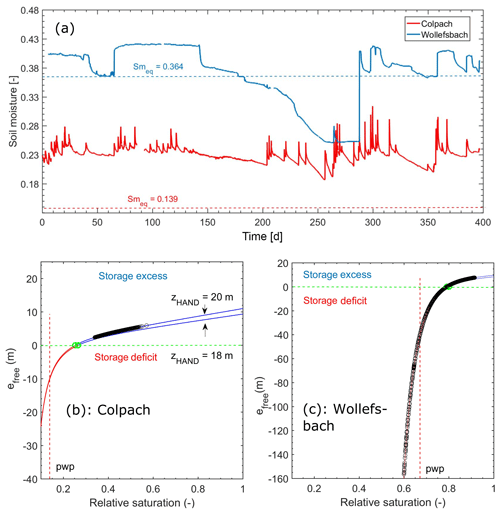
Figure 6Top soil water content observed at cluster sites in the Colpach and Wollefsbach catchments (a) and the corresponding free energy states in their respective energy state curves (b and c show the different scalings of the ordinates). The black circles mark the observations. The vertical dashed line marks the permanent wilting point. (b) and (c) show additionally the energy state curve when contaminating the real value of HAND with an error of −2 m (zHAND=18 m). This is to highlight that an error in the estimated depth to groundwater implies a substantial mismatch between observations and the theoretically predicted curve.
In the Wollefsbach the weight-specific free energy density of soil water spreads across a much wider range of almost 180 m, which corresponds to 1.79×106 J m−3 (Fig. 6c). The average specific free energy density is at −44.3 m ( J m−3) strongly negative, the distribution is highly skewed towards the negative value and the coefficient of variation is at 2.8 much larger. Most importantly the system operates qualitatively differently as it switches to the C-regime during the dry spell in the summer period and stays there for nearly 3 months. Please note that the free energy decreases to values which are clearly below the permanent wilting point pwp. (As specific free energy is the product of the total soil hydraulic potential and the soil water content, its value at the pwp does not simply correspond to −133 m.) To understand this strong decline in soil water content, it is important to recall that drying of the top 0.1 m of the soil is strongly influenced by evaporation and that the water potential of unsaturated air is at a relative humidity of 90 %, clearly below the permanent wilting point (Porada et al., 2011).
We hence state that the free energy state of the soil water stock reveals a distinctly different dynamic behaviour at both sites, which cannot be derived from the comparison of the corresponding soil water moisture time series. The Colpach site is characterized by permanent storage excess, though the corresponding soil water content is always smaller than in the Wollefsbach. Free energy of the soil water storage is in this range a linear function of relative saturation. This implies that the energy difference which predominantly drives soil water dynamics changes linearly with soil water content, or in other words gravity potential dominates against matric potential. The retention function in Fig. 1 shows that the matric potential in the Colpach at the minimum observed saturation of S=0.3 (Fig. 6b) equals −2 m. This implies according to Eq. (8) that 2 m + 0.3×θs 20 m = 2.91 m and that potential energy is 10 times larger than capillary binding energy. For higher saturations the first term remains rather constant, while the second increases linearly with saturation. In contrast, the Wollefsbach shows a strongly non-linear behaviour at this site and it switches to a storage deficit when the soil saturation drops below 0.79 (Fig. 6a). In a further step we contaminated the HAND values of both sites with an error of −2 m and plotted the corresponding energy state curves (zHAND=18 m). This curve does not match the observations (Fig. 6b and c). This proves (a) that HAND is a good estimator of depth to groundwater at these locations and (b) that an error in the estimated depth to groundwater leads to a mismatch between the theoretical energy state curve and the observed values. This implies that the observed energy states will also change with changing groundwater surface, as further detailed in the discussion.
4.2 Soil moisture and its free energy state within the entire observation domain
Figure 7 presents the free energy states of the soil moisture which was observed at all cluster sites in the Colpach (Fig. 7a, N=41) and the Wollefsbach (Fig. 7b, N=20). The respective heights above the channel range from 1 to 45 m in the Colpach and from 1 to 22 m in the Wollefsbach (Fig. 3b and c).
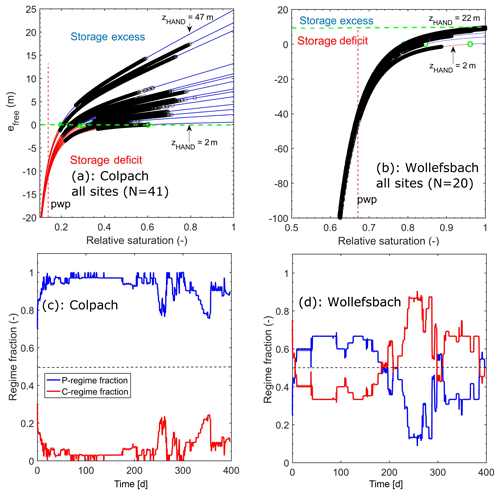
Figure 7Free energy of all observations in the Colpach (a) and Wollefsbach (b) plotted in their corresponding energy state function (note the different scales). The black circles mark the observations. The horizontal green lines mark the equilibrium of zero free energy. (c) and (d) show which fractions of the data set were in the P- or C-regime as a function of time. Note that the corresponding distributions of HAND are shown in Fig. 3b and c.
Generally, the observed free energy states plot nicely around the energy state curves of the corresponding HAND. The Colpach (except for a few sites) operates most of the time in the linear range of the P-regime, indicating that soil moisture dynamics is dominated by potential energy differences. Observations in the Colpach generally spread across a wide range of relative saturations, and the corresponding “amplitudes” of the free energy deviations are clearly larger than at the single site shown in Fig. 6b. This is because sensor clusters with the same HAND were pooled into the same subsample regardless of their separating distance. For instance, at zHAND=1 m the subsample consisted of one cluster with three replicate soil moisture profiles, and at zHAND=17 we had for instance three sensor clusters and thus in total eight soil moisture profiles. The partly large spreading of the observations may hence be explained by a combination of local-scale heterogeneity and large-scale differences in the drivers of soil water dynamics such as rainfall or local characteristics of forest vegetation.
Despite the large spreading, 80 % of the Colpach sites operated permanently in the P-regime (Fig. 7c). During the wet season it is more than 90 % of the sites, between days 250 and 400, and quite a few profiles switch to the C-regime and thus to a storage deficit. These profiles mostly have low HAND values, with only some having large values of 37 and 22 m.
In the Wollefsbach we find, consistent with Fig. 7b, a clear drop in free energy into the C-regime during the dry spell in the summer period. All sites drop clearly below the permanent wilting point, which corroborates the strong evaporative drying of the top soil in this landscape. In contrast to the Colpach, the fractions of profiles which operate in the different regimes are much more variable in time (Fig. 7d). During the observation period, on average 50 % of the profiles operate in the C-regime and thus in a storage deficit. The minimum is 30 % and the C-regime fraction peaks at 90 % at day 250. Note that more than 50 % of the sites are continuously in the C-regime during the second half of the observation period. These differences are consistent with the strongly different runoff generation behaviour of both systems, as further detailed in the next section.
4.3 Free energy state as control of streamflow generation
An interesting question is whether the free energy state of the soil water content and particularly the separation of the C- and P-regimes is helpful for explaining the onset of storage-controlled streamflow generation in both landscapes. As storage-controlled runoff response to rainfall is not generated everywhere in the catchment but mostly in the riparian zone, the energy state of soil water at large values of HAND is unimportant in this respect. We thus plotted for the entire hydrological year the observed streamflow in both catchments against the energy state of soil water for sites at the smallest HAND values of 2 m, which are close to the riparian zone (Fig. 8a and b).
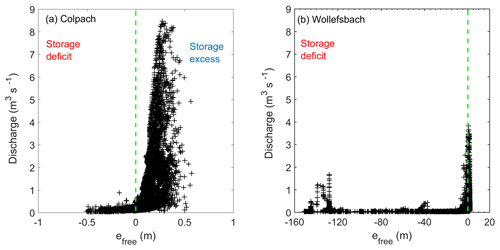
Figure 8Observed streamflow in the Colpach (a, drainage area is 19.2 km2) and the Wollefsbach (b, drainage area is 4.5 km2) plotted against the free energy of sites in their corresponding riparian zones.
Both scatter plots reveal distinct threshold-like dependence of streamflow on the free energy state of soil water and note that the threshold coincides with the state of zero free energy, which separates the C-regime from the P-regime. Streamflow in the Colpach is uniformly low if the riparian zone is in a storage deficit with respect to the local equilibrium (Fig. 8a), while streamflow shows a strong variability when the system switches to a storage excess in the P-regime. The transition to a state of storage excess, which implies that the system needs to release water to relax back to local equilibrium, coincides with the onset of storage-controlled streamflow generation. The variability of streamflow in the P-regime does of course also reflect the variability in the rainfall forcing. Streamflow in the C-regime likely feeds exclusively from groundwater. This behaviour is in line with our theoretical expectation.
In the Wollefsbach we observe a slightly different pattern. On the one hand there is a similar sharp increase in streamflow when free energy of soil water in the riparian zone switches from the C- to the P-regime. On the other hand one can observe distinct values of streamflow for specific free energy densities in the range between −1 and 10 m, at −40 m and below −120 m. This reflects infiltration excess runoff generation, which is frequently observed in this marl setting, as these states correspond to unsaturated hydraulic conductivities of either or m s−1 or even smaller values. Although overland flow also occurs in the Colpach, it only occurs on compacted forest roads, but not in the riparian zone or in upslope pristine areas.
The presented results provide evidence that a thermodynamic perspective on soil water storage offers holistic information for judging and inter-comparing soil water dynamics, which cannot be inferred from soil moisture observations alone. In the following we reflect on the general idea of using free energy as a state measure, and discuss its promises as well as its limiting assumptions. We then move on to the more specific differences in the storage dynamics in both studied catchments. And we close by reflecting on the apparent paradox between the known local non-linearity of soil physical characteristics and the frequent argumentation that hydrological systems often behave much more linearly.
5.1 Free energy and the energy state function – options and limitations
Our results show that free energy as a function of relative soil saturation holds the key to defining a meaningful state space of the root zone of a hydrological landscape. This space of possible energy states consists of a family of energy state curves, where each of those characterizes how free energy density evolves at a specific height above groundwater, depending on the triad of the matric potential, HAND (as a surrogate for the unknown gravity potential) and soil water content. The free energy state of soil water reflects in fact the balance between its capillary binding energy and geo-potential energy densities, and we showed that this balance determines
-
whether a system is at a given elevation above groundwater locally in its equilibrium storage state (efree=0), in a state of storage deficit (efree<0) or in a state of storage excess (efree>0), and
-
the regime of storage dynamics. Soil water dynamics in the C-regime (efree<0) are dominated by capillarity; i.e. differences in local matric potentials act as the dominant driver. The soil needs to recharge to relax to its local equilibrium, or it is in the P-regime (efree>0) dominated by potential energy; i.e. the non-local linear gravitational control dominates soil water dynamics, and the system needs to release water to relax to local equilibrium.
The energy level function turned out to be useful for inter-comparing distributed soil moisture observations among different hydrological landscapes, as it shows the trajectory of single sites or of the complete set of observations in its energy state space. This teaches us which part of the state space is actually “visited” by the system during the course of the year, whether the system operates predominantly in a single regime, whether it switches between both regimes during dry spells and how much water needs to be released or recharged locally for relaxing back to local equilibrium and how often it actually reaches its equilibrium.
Note that the usual comparison of soil water contents alone did not yield this information. On the contrary, from this we would conclude that the site in the Wollefsbach is, due to the higher soil water content, always “wetter” than the corresponding site in the Colpach. The free energy state reveals, however, the exact opposite: we have a storage excess at the Colpach site for the entire year, while the Wollefsbach site is in summer in a storage deficit. We thus propose that the terms “wet” and “dry” should only be used with respect to the equilibrium storage as a meaningful reference point.
The free energy state of soil water in the riparian zone of both study catchments has furthermore been proven to be rather helpful in explaining streamflow generation. We found a distinct threshold behaviour for storage-controlled runoff production in both catchments, and clear hints at overland flow contributions in the Wollefsbach. While we admit that a threshold-like dependence of runoff generation is frequently reported (Tromp-van and McDonnell, 2006a, b), we would like to stress that the tipping point we found here has a theoretical basis. In both catchments it coincides with the local equilibrium state of zero free energy – the onset of a potential energy excess of soil water in the riparian zone coincides with the onset of a strongly enlarged streamflow generation.
The apparent strong sensitivity of the free energy state of soil water to the estimated depth to groundwater offers new opportunities for data-based learning and an improved design of measurement campaigns, but it also determines the limits of the proposed approach. With respect to the first aspect, we could show that an underestimation of 2 m in the assumed depth to groundwater leads to a clear deviation of the observed free energy states from the theoretical energy level curve. This offers the opportunity to estimate depth to groundwater from joint observations of soil moisture and matric potential, in case the local retention function is known. This can, for instance, be done by minimizing the residuals between the observation and the theoretical curve as a function of depth to groundwater, or it allows for the derivation of a retention function based on the joint observations of soil moisture, matric potential and depth to groundwater. Here, we need to minimize the residuals between the observation and the theoretical curve, but this time as a function of the parameters of the soil water retention curve. Due to this strong sensitivity it is furthermore important to stratify soil moisture observations both according to the installed depth of the sensor and according to the elevation of the site above groundwater, or the height over the next stream. The latter is important because depth to groundwater determines the equilibrium storage the site will approach when relaxing from external forcing.
Despite all these opportunities for learning, the sensitivity of free energy to the estimated depth to groundwater implies that the site of the system is still in hydraulic contact with the aquifer. This key assumption is certainly violated if the soil gets so dry that the water phase becomes immobile while the air phase becomes the mobile phase. And it might get violated if depth to groundwater becomes too large. Last but not least, the groundwater surface may change either seasonally or in some systems more rapidly, and this might imply step changes in the energy state function and the storage equilibrium.
We nevertheless conclude that it is worth collecting joint data sets either of the triple of soil moisture, matric potential and the retention function at distributed locations (as we did in the CAOS research unit as explained in Zehe et al., 2014) or even preferably of the quadruple of soil moisture, matric potential, retention function and depth to groundwater. Soil moisture observations alone appear to be not very informative about the system state. This is because they neither tell anything about the binding state of water nor about how the system deviates from its equilibrium and which process is “needed” to relax.
5.2 Storage dynamics in different landscapes – local versus non local controls
In line with our proposition, we found a distinctly typical interplay between capillary and gravitational controls on soil water in our study areas, which were in the Colpach were substantially different compared to the Wollefsbach. The observations clearly revealed that the topsoil in the Colpach operates the entire hydrological year largely in a state of storage excess due to an overshoot in potential energy. Soil water dynamics is mainly driven by differences in potential energy, which means that the linear and non-local gravitational control dominates. Most interestingly we found that the free energy state of the soil operated for a considerable time of the year in the linear range of the P-regime, which implies that the storage dynamics is (multi-)linear. This means that the specific free energy density is at each HAND level a linear function of relative saturation, but the slope of the energy state curves does increase with increasing geopotential. We found furthermore that the annual variation of the averaged free energy of the soil water storage was rather small. Zehe et al. (2013) found a similar, almost steady-state behaviour for the averaged free energy of the soil water storage in the Mallalcahuello catchment in Chile, which also operated in the P-regime the entire year. Note that both landscapes are characterized by a pronounced topography, by well-drained highly porous soils (Blume et al., 2008a, b, 2009), and that both are predominantly forested. In both landscapes, subsurface storm flow and thus storage-controlled runoff generation are the dominant mechanisms of streamflow generation. This is consistent with our finding that gravity is the dominant control of soil water dynamics.
In contrast, the Wollefsbach was characterized by a seasonal change between both regimes: operation in the P-regime during the wet season and a drop to a C-regime and a storage deficit during the dry summer period. Free energy was at all sites on average negative, and a non-linear function of the relative saturation. Interestingly we found the same seasonality for the Weiherbach catchment in Germany, a dominance of potential energy during the wet season and a strong dominance of capillary surface energy in summer (Zehe et al., 2013). Note that both landscapes are characterized by cohesive soils, more silty in the Weiherbach and more clay-rich in the Wollefsbach, and a gentle topography. And both are used for agriculture. In both areas Hortonian overland flow would play the dominant role, but this process is actually strongly reduced due to a large number of worm burrows acting as macropores (Zehe and Blöschl, 2004; Schneider et al., 2018). Both landscapes are also controlled by tile drains. In both areas the soil water dynamics is dominated by capillarity during the summer period, which means that the local soil physical control dominates root zone soil moisture dynamics.
5.3 Concluding remarks
Overall we conclude that a thermodynamic perspective on hydrological systems provides valuable insights, helping us to better understand and characterize different landscapes. Given the strong relation between a potential energy excess of soil water in the riparian zone and strongly enlarged streamflow production, we found in our study areas that it seems promising to further explore the value of free energy for hydrological predictions. We also conclude that it makes sense to use the terms “wet” and “dry” only with respect to the equilibrium storage as a meaningful reference point, because the latter determines whether the soil is in a state of storage excess or a storage deficit with respect to the free energy state. Another key finding is that the energy level function, which can be seen as a straightforward generalization of the soil retention function, accounts jointly for capillary and gravitational control on soil moisture dynamics. With this we link the non-linear soil physical control and the topographical control on storage dynamics in a stratified manner and use HAND as a surrogate for the gravitational potential. A nice additional finding is that a linear dependence of free energy on soil saturation does not compromise the non-linearity of soil water characteristics. On the contrary, it may be explained by the dominance of potential energy in catchments with pronounced topography and during not too dry conditions, and this implies that at least the energy difference driving soil water dynamics is a linear function of the stored water amount. The latter is the basis of the linear reservoir, which is frequently used in conceptual modelling. The option for linear behaviour of the subsurface is hence inherent not only to Darcy's law of the saturated zone, as has been shown by de Rooij (2013) by deriving aquifer-scale flow equations for strip aquifers. Even in the top of the unsaturated zone a linear relation between storage and driving potential energy differences might emerge. This inherent option for linear behaviour is likely the reason why conceptual models, which usually do not account for soil physical characteristics, work very well in some catchments, while in others they do not. Based on the presented findings one could speculate that conceptual models work well in systems which are dominated by potential energy.
The code and the data underlying this study are freely available by email request to the contact author.
EZ wrote the paper, had the main idea for the underlying theoretical framework and carried out most of the analysis. RL and CJ contributed both to the theoretical framework, derived the distribution functions of HAND in both study catchments and measured the effective soil water retention curves. MW, AK and HHS contributed strongly to the idea of the energy state functions and their thermodynamic interpretation. SKH and TB collected the soil water content and matric potential data in the field and provided quality controlled data for the analysis.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Thermodynamics and optimality in the Earth system and its subsystems (ESD/HESS inter-journal SI)”. It is not associated with a conference.
We sincerely thank both reviewers, particularly Gerrit de Rooij, for their
thoughtful and valuable feedback. This study contributes to and greatly
benefited from the “Catchments as Organized Systems” (CAOS) research unit.
We thank the German Research Foundation (DFG) for funding (FOR 1598,
ZE 533/11-1, ZE 533/12-1). The authors acknowledge support by the Deutsche
Forschungsgemeinschaft and the Open Access Publishing Fund of the Karlsruhe
Institute of Technology (KIT). The service charges for this open-access
publication have been covered by a Research Centre of the Helmholtz
Association.
The article processing charges for this open-access
publication
were covered by a Research
Centre of the Helmholtz Association.
Edited by: Stefan Hergarten
Reviewed by: Gerrit H. de Rooij and one anonymous referee
Angermann, L., Jackisch, C., Allroggen, N., Sprenger, M., Zehe, E., Tronicke, J., Weiler, M., and Blume, T.: Form and function in hillslope hydrology: Characterization of subsurface flow based on response observations, Hydrol. Earth Syst. Sci., 21, 3727–3748, https://doi.org/10.5194/hess-21-3727-2017, 2017.
Beven, K.: Searching for the Holy Grail of scientific hydrology: Qt=(S, R, Δt)A as closure, Hydrol. Earth Syst. Sci., 10, 609–618, https://doi.org/10.5194/hess-10-609-2006, 2006.
Blume, T., Zehe, E., and Bronstert, A.: Investigation of runoff generation in a pristine, poorly gauged catchment in the chilean andes ii: Qualitative and quantitative use of tracers at three spatial scales, Hydrol. Process., 22, 3676–3688, https://doi.org/10.1002/hyp.6970, 2008a.
Blume, T., Zehe, E., Reusser, D. E., Iroume, A., and Bronstert, A.: Investigation of runoff generation in a pristine, poorly gauged catchment in the chilean andes i: A multi-method experimental study, Hydrol. Process., 22, 3661–3675, https://doi.org/10.1002/hyp.6971, 2008b.
Blume, T., Zehe, E., and Bronstert, A.: Use of soil moisture dynamics and patterns at different spatio-temporal scales for the investigation of subsurface flow processes, Hydrol. Earth Syst. Sci., 13, 1215–1233, https://doi.org/10.5194/hess-13-1215-2009, 2009.
Bolt, G. H. and Frissel, M. J.: Thermodynamics of soil moisture, Neth. J. Agricult. Sci., 8, 57–78, 1960.
Budyko, M. I.: The heat balance of the earth's surface, US Dept. of Commerce, Washington, 1958.
de Rooij, G. H.: Averaging hydraulic head, pressure head, and gravitational head in subsurface hydrology, and implications for averaged fluxes, and hydraulic conductivity, Hydrol. Earth Syst. Sci., 13, 1123–1132, https://doi.org/10.5194/hess-13-1123-2009, 2009.
de Rooij, G. H.: Averaged water potentials in soil water and groundwater, and their connection to menisci in soil pores, field-scale flow phenomena, and simple groundwater flows, Hydrol. Earth Syst. Sci., 15, 1601–1614, https://doi.org/10.5194/hess-15-1601-2011, 2011.
de Rooij, G. H.: Aquifer-scale flow equations as generalized linear reservoir models for strip and circular aquifers: Links between the Darcian and the aquifer scale, Water Resour. Res., 49, 8605–8615, https://doi.org/10.1002/2013WR014873, 2013.
Edlefson, N. E. and Anderson, A. B. C.: Thermodynamics of soil moisture, Hilgardia, 15, 31, 1940.
Gao, H., Hrachowitz, M., Schymanski, S. J., Fenicia, F., Sriwongsitanon, N., and Savenije, H. H. G.: Climate controls how ecosystems size the root zone storage capacity at catchment scale, Geophys. Res. Lett., 41, 7916–7923, https://doi.org/10.1002/2014gl061668, 2014.
Graeff, T., Zehe, E., Reusser, D., Lück, E., Schröder, B., Wenk, G., John, H., and Bronstert, A.: Process identification through rejection of model structures in a mid-mountainous rural catchment: Observations of rainfall-runoff response, geophysical conditions and model inter-comparison, Hydrol. Process., 23, 702–718, https://doi.org/10.1002/hyp.7171, 2009.
Hergarten, S., Winkler, G., and Birk, S.: Transferring the concept of minimum energy dissipation from river networks to subsurface flow patterns, Hydrol. Earth Syst. Sci., 18, 4277–4288, https://doi.org/10.5194/hess-18-4277-2014, 2014.
Hildebrandt, A., Kleidon, A., and Bechmann, M.: A thermodynamic formulation of root water uptake, Hydrol. Earth Syst. Sci., 20, 3441–3454, https://doi.org/10.5194/hess-20-3441-2016, 2016.
Hillel, D.: Introduction to Environmental Soil Physics, Elsevier Acacemic Press, Amsterdam, Boston, Heidelberg, London, ISBN-13:978-0-12-348655-4, p. 494, 2004.
Howard, A. D.: Optimal angles of stream junctions: geometric stability to capture and minimum power criteria, Water Resourc. Res., 7, 863–873, 1971.
Howard, A. D.: Theoretical model of optimal drainage networks, Water Resour. Res., 26, 2107–2117, 1990.
Jackisch, C.: Linking structure and functioning of hydrological systems – How to achieve necessary experimental and model complexity with adequate effort, PhD thesis, KIT Karlsruhe Institute of Technology, Karlsruhe, https://doi.org/10.5445/IR/1000051494, 2015.
Jackisch, C., Angermann, L., Allroggen, N., Sprenger, M., Blume, T., Tronicke, J., and Zehe, E.: Form and function in hillslope hydrology: In situ imaging and characterization of flow-relevant structures, Hydrol. Earth Syst. Sci., 21, 3749–3775, https://doi.org/10.5194/hess-21-3749-2017, 2017.
Kleidon, A., and Schymanski, S.: Thermodynamics and optimality of the water budget on land: A review, Geophys. Res. Lett., 35, L20404, https://doi.org/10.1029/2008gl035393, 2008.
Kleidon, A., Zehe, E., Ehret, U., and Scherer, U.: Thermodynamics, maximum power, and the dynamics of preferential river flow structures at the continental scale, Hydrol. Earth Syst. Sci., 17, 225–251, https://doi.org/10.5194/hess-17-225-2013, 2013.
Kleidon, A., Renner, M., and Porada, P.: Estimates of the climatological land surface energy and water balance derived from maximum convective power, Hydrol. Earth Syst. Sci., 18, 2201–2218, https://doi.org/10.5194/hess-18-2201-2014, 2014.
Koehler, B., Corre, M. D., Steger, K., Well, R., Zehe, E., Sueta, J. P., and Veldkamp, E.: An in-depth look into a tropical lowland forest soil: Nitrogen-addition effects on the contents of N2O, CO2 and CH4 and N2O isotopic signatures down to 2-m depth, Biogeochemistry, 111, 695–713, https://doi.org/10.1007/s10533-012-9711-6, 2012.
Lee, H., Sivapalan, M., and Zehe, E.: Representative elementary watershed (rew) approach, a new blueprint for distributed hydrologic modelling at the catchment scale: The development of closure relations, in: Predicting ungauged streamflow in the mackenzie river basin: Today's techniques and tomorrow's solutions, edited by: Spence, C., Pomeroy, J., and Pietroniro, A., Canadian Water Resources Association (CWRA), Ottawa, 165–218, 2005.
Lee, H., Zehe, E., and Sivapalan, M.: Predictions of rainfall-runoff response and soil moisture dynamics in a microscale catchment using the CREW model, Hydrol. Earth Syst. Sci., 11, 819–849, https://doi.org/10.5194/hess-11-819-2007, 2007.
Leopold, L. B. and Langbein, W. L.: The concept of entropy in landscape evolution, US Geol. Surv. Prof. Pap. 500-A, United States Govermental Printing Office, Washington, 1962.
Loritz, R., Hassler, S. K., Jackisch, C., Allroggen, N., van Schaik, L., Wienhöfer, J., and Zehe, E.: Picturing and modeling catchments by representative hillslopes, Hydrol. Earth Syst. Sci., 21, 1225–1249, https://doi.org/10.5194/hess-21-1225-2017, 2017.
Loritz, R., Gupta, H., Jackisch, C., Westhoff, M., Kleidon, A., Ehret, U., and Zehe, E.: On the dynamic nature of hydrological similarity, Hydrol. Earth Syst. Sci., 22, 3663–3684, https://doi.org/10.5194/hess-22-3663-2018, 2018.
Lotka, A. J.: Contribution to the energetics of evolution, P. Natl. Acad. Sci. USA, 8, 147–151, 1922a.
Lotka, A. J.: Natural selection as a physical principle, P. Natl. Acad. Sci. USA, 8, 151–154, 1922b.
Martinez-Carreras, N., Wetzel, C. E., Frentress, J., Ector, L., McDonnell, J. J., Hoffmann, L., and Pfister, L.: Hydrological connectivity inferred from diatom transport through the riparian-stream system, Hydrol. Earth Syst. Sci., 19, 3133–3151, https://doi.org/10.5194/hess-19-3133-2015, 2015.
Nobre, A. D., Cuartas, L. A., Hodnett, M., Renno, C. D., Rodrigues, G., Silveira, A., Waterloo, M., and Saleska, S.: Height above the nearest drainage – a hydrologically relevant new terrain model, J. Hydrol., 404, 13–29, https://doi.org/10.1016/j.jhydrol.2011.03.051, 2011.
Paltridge, G. W.: Climate and thermodynamic systems of maximum dissipation, Nature, 279, 630–631, https://doi.org/10.1038/279630a0, 1979.
Pfister, L., Iffly, J., and Hoffmann, L.: Use of regionalized stormflow coefficients with a view to hydroclimatological hazard mapping, Hydrolog. Sci. J. – Journal Des Sciences Hydrologiques, 47, 479–491, 2002.
Pfister, L., Martinez-Carreras, N., Hissler, C., Klaus, J., Carrer, G. E., Stewart, M. K., and McDonnell, J. J.: Bedrock geology controls on catchment storage, mixing, and release: A comparative analysis of 16 nested catchments, Hydrol. Process., 31, 1828–1845, https://doi.org/10.1002/hyp.11134, 2017.
Porada, P., Kleidon, A., and Schymanski, S. J.: Entropy production of soil hydrological processes and its maximisation, Earth Syst. Dynam., 2, 179–190, https://doi.org/10.5194/esd-2-179-2011, 2011.
Reggiani, P., Hassanizadeh, S. M., and Sivapalan, M.: A unifying framework for watershed thermodynamics: Balance equations for mass, momentum, energy and entropy, and the second law of thermodynamics, Adv. Water Resour., 22, 367–398, 1998.
Reggiani, P., Hassanizadeh, S. M., Sivapalan, M., and Gray, W. G.: A unifying framework for watershed thermodynamics: Constitutive relationships, Adv. Water Resour., 23, 15–39, 1999.
Reggiani, P., Sivapalan, M., and Hassanizadeh, S. M.: Conservation equations governing hillslope responses: Exploring the physical basis of water balance, Water Resour. Res., 36, 1845–1863, 2000.
Reggiani, P. and Schellekens, J.: Modelling of hydrological responses: The representative elementary watershed approach as an alternative blueprint for watershed modelling, Hydrol. Process., 17, 3785–3789, 2003.
Renner, M., Hassler, S. K., Blume, T., Weiler, M., Hildebrandt, A., Guderle, M., Schymanski, S. J., and Kleidon, A.: Dominant controls of transpiration along a hillslope transect inferred from ecohydrological measurements and thermodynamic limits, Hydrol. Earth Syst. Sci., 20, 2063–2083, https://doi.org/10.5194/hess-20-2063-2016, 2016.
Renno, C. D., Nobre, A. D., Cuartas, L. A., Soares, J. V., Hodnett, M. G., Tomasella, J., and Waterloo, M. J.: Hand, a new terrain descriptor using srtm-dem: Mapping terra-firme rainforest environments in amazonia, Remote Sens. Environ., 112, 3469–3481, https://doi.org/10.1016/j.rse.2008.03.018, 2008.
Rinaldo, A., Maritan, A., Colaiori, F., Flammini, A., and Rigon, R.: Thermodynamics of fractal networks, Phys. Rev. Lett., 76, 3364–3367, 1996.
Saco, P. M., and Moreno-de las Heras, M.: Ecogeomorphic coevolution of semiarid hillslopes: Emergence of banded and striped vegetation patterns through interaction of biotic and abiotic processes, Water Resour. Res., 49, 115–126, https://doi.org/10.1029/2012wr012001, 2013.
Savenije, H. H. G. and Hrachowitz, M.: Hess opinions “catchments as meta-organisms – a new blueprint for hydrological modelling”, Hydrol. Earth Syst. Sci., 21, 1107–1116, https://doi.org/10.5194/hess-21-1107-2017, 2017.
Schneider, A. K., Hohenbrink, T. L., Reck, A., Zangerle, A., Schroder, B., Zehe, E., and van Schaik, L.: Variability of earthworm-induced biopores and their hydrological effectiveness in space and time, Pedobiologia, 71, 8–19, https://doi.org/10.1016/j.pedobi.2018.09.001, 2018.
Seibert, S. P., Jackisch, C., Ehret, U., Pfister, L., and Zehe, E.: Unravelling abiotic and biotic controls on the seasonal water balance using data-driven dimensionless diagnostics, Hydrol. Earth Syst. Sci., 21, 2817–2841, https://doi.org/10.5194/hess-21-2817-2017, 2017.
Sivapalan, M.: From engineering hydrology to earth system science: Milestones in the transformation of hydrologic science, Hydrol. Earth Syst. Sci., 22, 1665–1693, https://doi.org/10.5194/hess-22-1665-2018, 2018.
Sivapalan, M. and Bloschl, G.: Time scale interactions and the coevolution of humans and water, Water Resour. Res., 51, 6988–7022, https://doi.org/10.1002/2015wr017896, 2015.
Tian, F., Hu, H., Lei, Z., and Sivapalan, M.: Extension of the Representative Elementary Watershed approach for cold regions via explicit treatment of energy related processes, Hydrol. Earth Syst. Sci., 10, 619–644, https://doi.org/10.5194/hess-10-619-2006, 2006.
Tietjen, B., Zehe, E., and Jeltsch, F.: Simulating plant water availability in dry lands under climate change: A generic model of two soil layers, Water Resour. Res., 45, W01418, https://doi.org/10.1029/2007wr006589, 2009.
Tietjen, B., Jeltsch, F., Zehe, E., Classen, N., Groengroeft, A., Schiffers, K., and Oldeland, J.: Effects of climate change on the coupled dynamics of water and vegetation in drylands, Ecohydrology, 3, 226–237, https://doi.org/10.1002/eco.70, 2010.
Troch, P. A., Lahmers, T., Meira, A., Mukherjee, R., Pedersen, J. W., Roy, T., and Valdes-Pineda, R.: Catchment coevolution: A useful framework for improving predictions of hydrological change?, Water Resour. Res., 51, 4903–4922, https://doi.org/10.1002/2015wr017032, 2015.
Tromp-van Meerveld, H. J. and McDonnell, J. J.: Threshold relations in subsurface stormflow 1. A storm analysis of the panola hillslope, Water Resour. Res., 42, W02410, https://doi.org/10.01029/02004WR003778, 2006a.
Tromp-van Meerveld, H. J. and McDonnell, J. J.: Threshold relations in subsurface stormflow: 2. The fill and spill hypothesis, Water Resour. Res., 42, W02411, https://doi.org/10.1029/2004wr003800, 2006b.
Westhoff, M., Kleidon, A., Schymanski, S., Dewals, B., Nijsse, F., Renner, M., Dijkstra, H., Ozawa, H., Savenije, H., Dolman, H., Meesters, A., and Zehe, E.: ESD Reviews: Thermodynamic optimality in Earth sciences. The missing constraints in modeling Earth system dynamics?, Earth Syst. Dynam. Discuss., https://doi.org/10.5194/esd-2019-6, in review, 2019.
Westhoff, M. C. and Zehe, E.: Maximum entropy production: Can it be used to constrain conceptual hydrological models?, Hydrol. Earth Syst. Sci., 17, 3141–3157, https://doi.org/10.5194/hess-17-3141-2013, 2013.
Westhoff, M. C., Zehe, E., and Schymanski, S. J.: Importance of temporal variability for hydrological predictions based on themaximum entropy production principle, Geophys. Res. Lett., 41, 67–73, https://doi.org/10.1002/2013gl058533, 2014.
Wrede, S., Fenicia, F., Martinez-Carreras, N., Juilleret, J., Hissler, C., Krein, A., Savenije, H. H. G., Uhlenbrook, S., Kavetski, D., and Pfister, L.: Towards more systematic perceptual model development: A case study using 3 luxembourgish catchments, Hydrol. Process., 29, 2731–2750, https://doi.org/10.1002/hyp.10393, 2015.
Zehe, E., and Blöschl, G.: Predictability of hydrologic response at the plot and catchment scales: Role of initial conditions, Water Resour. Res., 40, W10202, https://doi.org/10.1029/2003wr002869, 2004.
Zehe, E., Lee, H., and Sivapalan, M.: Dynamical process upscaling for deriving catchment scale state variables and constitutive relations for meso-scale process models, Hydrol. Earth Syst. Sci., 10, 981–996, https://doi.org/10.5194/hess-10-981-2006, 2006.
Zehe, E., Blume, T., and Bloschl, G.: The principle of `maximum energy dissipation': A novel thermodynamic perspective on rapid water flow in connected soil structures, Philos. T. Roy. Soc. B, 365, 1377–1386, https://doi.org/10.1098/rstb.2009.0308, 2010a.
Zehe, E., Graeff, T., Morgner, M., Bauer, A., and Bronstert, A.: Plot and field scale soil moisture dynamics and subsurface wetness control on runoff generation in a headwater in the Ore Mountains, Hydrol. Earth Syst. Sci., 14, 873–889, https://doi.org/10.5194/hess-14-873-2010, 2010b.
Zehe, E., Ehret, U., Blume, T., Kleidon, A., Scherer, U., and Westhoff, M.: A thermodynamic approach to link self-organization, preferential flow and rainfall-runoff behaviour, Hydrol. Earth Syst. Sci., 17, 4297–4322, https://doi.org/10.5194/hess-17-4297-2013, 2013.
Zehe, E., Ehret, U., Pfister, L., Blume, T., Schroder, B., Westhoff, M., Jackisch, C., Schymanski, S. J., Weiler, M., Schulz, K., Allroggen, N., Tronicke, J., van Schaik, L., Dietrich, P., Scherer, U., Eccard, J., Wulfmeyer, V., and Kleidon, A.: Hess opinions: From response units to functional units: A thermodynamic reinterpretation of the hru concept to link spatial organization and functioning of intermediate scale catchments, Hydrol. Earth Syst. Sci., 18, 4635–4655, https://doi.org/10.5194/hess-18-4635-2014, 2014.
Zhang, G. P., Savenije, H. H. G., Fenicia, F., and Pfister, L.: Modelling subsurface storm flow with the Representative Elementary Watershed (REW) approach: application to the Alzette River Basin, Hydrol. Earth Syst. Sci., 10, 937–955, https://doi.org/10.5194/hess-10-937-2006, 2006.





