A review of methods for measuring groundwater–surface water exchange in braided rivers

Braided rivers, while uncommon internationally, are significant in terms of their unique ecosystems and as vital freshwater resources at locations where they occur. With an increasing awareness of the connected nature of surface water and groundwater, there have been many studies examining groundwater–surface water exchange in various types of waterbodies, but significantly less research has been conducted in braided rivers. Thus, there is currently limited understanding of how characteristics unique to braided rivers, such as channel shifting, expanding and narrowing margins, and a high degree of heterogeneity affect groundwater–surface water flow paths. This article provides an overview of characteristics specific to braided rivers, including a map showing the regions where braided rivers are mainly found at the global scale: Alaska, Canada, the Japanese and European Alps, the Himalayas, Russia, and New Zealand. To the authors' knowledge, this is the first map of its kind. This is followed by a review of prior studies that have investigated groundwater–surface water interactions in braided rivers and their associated aquifers. The various methods used to characterise these processes are discussed with emphasis on their effectiveness in achieving the studies' objectives and their applicability in braided rivers. We also discuss additional methods that appear promising to apply in braided river settings. The aim is to provide guidance on methodologies most suitable for future work in braided rivers. In many cases, previous studies found a multi-method approach useful to produce more robust results and compare data collected at various scales. Given the challenges of working directly in braided rivers, there is considerable scope for the increased use of remote sensing techniques. There is also opportunity for new approaches to modelling braided rivers using integrated techniques that incorporate the complex river bed terrain and geomorphology of braided rivers explicitly. We also identify a critical need to improve the conceptual understanding of hyporheic exchange in braided rivers, rates of recharge to and from braided rivers, and historical patterns of dry and low-flow periods in these rivers.

1 Introduction

Until recently, groundwater and surface water systems were often considered separately both in research and in the way they were managed as resources (Kalbus et al., 2006; Winter et al., 1998). However, understanding the interactions between groundwater and surface water is now recognised as crucial to effective water resource management (Brodie et al., 2007). These systems are connected, so the development or contamination of either groundwater or surface water will often affect the other (Rosenberry and LaBaugh, 2008). Pumping from wells that are hydraulically connected to surface water bodies can result in, for example, reduced flows in rivers or diminished lake levels, or cause surface water inflow to groundwater (Stefania et al., 2018). Locations where groundwater and surface water interact can serve as contaminant transport pathways (Chadwick et al., 2002). Groundwater seepage into surface water can provide important nutrients and temperature regulation for aquatic organisms (Hayashi and Rosenberry, 2002). Key questions in groundwater–surface water investigations are the location and flux of groundwater discharge to surface water bodies and, conversely, surface water recharge to groundwater. These questions can be considered at various spatial and temporal scales (Fleckenstein et al., 2010; González-Pinzón et al., 2015; Magliozzi et al., 2018).

This paper often refers to groundwater–surface water exchange, which in this context may include regional groundwater exchange with river water, as well as hyporheic zone exchange. The hyporheic zone consists of the sediments surrounding a river that are permeated by stream water (Boano et al., 2014). Hyporheic flow consists of river water that enters the hyporheic zone and re-emerges at the surface at some location downstream (Boano et al., 2014). Groundwater may also mix with surface water in the hyporheic zone (Boano et al., 2014). Hyporheic zone flow is multi-directional and may occur at multiple temporal and spatial scales (Cardenas, 2015). It is critical to note that there have been very few studies examining the hydrology and conceptualisation of the hyporheic zone in braided rivers. This is a crucial gap in knowledge, as this often limits our ability to interpret data collected from braided rivers relating to groundwater–surface water exchange.

This article investigates the methods that have previously been used for examining groundwater–surface water exchange in braided rivers and discusses scope for new methods to be applied. Braided rivers are a highly dynamic type of river with meandering channels, wide bars and variable flow levels. Globally, braided rivers are relatively rare; they are mainly found in the Canadian Rockies, Alaska, the Himalayas, New Zealand, Russia, and the European and Japanese Alps (Fig. 1) (Tockner et al., 2006; Alexeevsky et al., 2013). There are instances of braided rivers at locations outside of these regions (e.g. the US, Scotland, Iceland, China, Poland, Belarus, Colombia, Congo, Brazil, Paraguay, Argentina, and the Touat Valley in Africa); however, these locations are not shown in Fig. 1 because, at a global scale, they are not where braided rivers are mainly found. The regions displayed in Fig. 1 are regularly cited in literature on braided rivers as the main regions where this river type can be found (Hibbert and Brown, 2001; Tockner et al., 2006). Braided rivers generally occur in mountainous areas with a large sediment source (such as glacial outwash), high river discharge rates and a steep topographic gradient (Charlton, 2008). These high-energy environments enable the rivers to carry large sediment loads. When these rivers reach their capacity to carry sediment, they form gravel braids, which branch out and re-join, creating gravel islands and shallow bars (Figs. 2 and 3). Bars and islands are often referred to as distinct features, with bars existing at periods of low flow, while islands are generally more permanent features that may be vegetated (Charlton, 2008). Braided rivers can completely change their geometry over a few decades. They undergo expansion and contraction phases in which their channels widen or narrow, depending on sediment supply and river flows (Piégay et al., 2006). The wetted channels of the river can shift, abandoning channels and re-occupying old channels (Charlton, 2008). Relatively erodible streambanks, which allow for wide channels to form and meander, are a key characteristic of braided rivers. These rivers generally have gravel beds but sand-bed rivers such as the Brahmaputra–Jamuna, which begins in the Himalayas and flows through India and Bangladesh (and is the world's largest braided river), can also form braided patterns (Sarker et al., 2014). The Brahmaputra–Jamuna is the only braided river in this review that is not a gravel-bed braided river. Also, it is important to note, the specific rivers discussed in this article are all braided rivers unless otherwise mentioned.

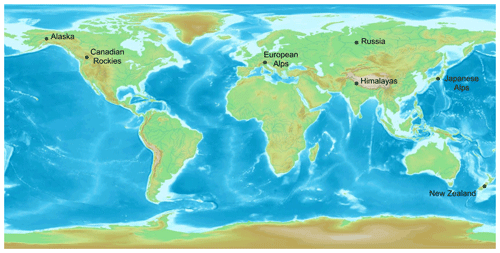
Figure 1 Locations where most braided rivers occur globally. Map base layer image attribution: “World Map-A non-Frame” is licensed under CC BY-SA 3.0.

Figure 2 Rakaia River in New Zealand displaying a classic braided pattern. Image reproduced with permission by Andrew Cooper.

Figure 3 The Rakahuri/Ashley River in New Zealand displaying a typical braided river consisting of multiple channels, gravel bars and vegetated islands. Photo: Katie Coluccio.

Braided river deposits have formed extensive aquifers throughout the world including many in the regions shown in Fig. 1 (Brown, 2001; Huggenberger and Regli, 2006). The complex depositional processes of braided rivers create heterogeneous aquifer properties (Huggenberger and Regli, 2006), and a significant portion of flow occurs at varying scales in preferential flow paths formed by previous river flow channels (Close et al., 2014; Dann et al., 2008; White, 2009). The complexity of braided rivers and their underlying heterogeneous aquifers makes managing these systems in an integrated manner, that accounts for surface water-groundwater interaction, challenging. For example, there is significant uncertainty surrounding rates of groundwater recharge from large braided rivers in New Zealand, which complicates the sustainable allocation of water extraction rights from surface water and groundwater sources (Close et al., 2014). There is also limited knowledge of how hyporheic flow processes operate and how they impact river flow levels and water quality in braided rivers. Braided rivers also often have reaches that become dry or have very low flows at the surface. The historical patterns of these drying and low-flow periods, and the impact of groundwater–surface water exchange on this, is an area of research where improved knowledge is needed. For example, many irrigation schemes have artificially raised groundwater levels due to land surface recharge, or lowered groundwater levels due to abstraction in comparison to their pre-irrigation states. In some rivers this has affected their losing/gaining patterns (Burbery and Ritson, 2010; Riegler, 2012).

Braided rivers around the world have ecological, cultural, social, economic and recreational importance. They provide habitat for many plant and animal species specifically adapted to survive in the dynamic, nutrient-poor environment of the rivers' gravel bars and their margins (Kilroy et al., 2004; Tockner et al., 2006). In New Zealand, the rivers are some of the last remaining native habitat on the heavily modified Canterbury Plains of the South Island, thus serving a vital ecological purpose for plant and animal species, many of which are critically endangered (Caruso, 2006; Williams and Wiser, 2004). Braided rivers and their associated aquifers are also important freshwater resources used for drinking water supplies, irrigation, stock water and hydropower. In many areas, these rivers hold significant cultural, social and recreational value for their importance for food gathering, boating and swimming, and as places of outstanding natural character.

However, braided rivers face pressure from many angles. In many places they are subject to damage from vehicles, gravel extraction, invasive plant species, development on river margins, damming, land encroachment, containment through flood engineering, low-flow levels and poor water quality (Caruso, 2006; Larned et al., 2008; Tockner and Stanford, 2002). These factors can influence river processes in many ways, including altering the rate of sedimentation or changing the flow regime, which may impact various uses of these rivers, as well as riparian ecosystems (Piégay et al., 2006).

Much braided river research has focused on understanding their geomorphological structures and processes, such as sediment transport (e.g. Ashmore, 1993; Chalov and Alexeevsky, 2015; Huggenberger and Regli, 2006; Nicholas et al., 2006). The majority of studies up to the early 1990s consisted of laboratory-based modelling of the braiding process (e.g. Ashmore, 1982; Young and Davies, 1991) and field studies of small reaches of valley-confined systems (Ferguson et al., 1992). Beginning in the mid-1990s, there were advances in numerical models to estimate the braiding process in reaches, remote sensing, and the quantification of river morphology and morphological change using digital elevation models (e.g. Bernini et al., 2006; Copley and Moore, 1993; Doeschl et al., 2006; Huggenberger, 1993). This allowed, for the first time, the visualisation and analysis of the morphology of large braided rivers (e.g. Hicks et al., 2006; Huggenberger, 1993; Lane, 2006). A number of studies have looked at the surface water features of braided rivers (e.g. Davies et al., 1996; Meunier et al., 2006; Young and Warburton, 1996), as well as aquifers created by braided river deposits (e.g. Huber and Huggenberger, 2016; Pirot et al., 2015; Vienken et al., 2017). However, the connections between the two have been less explored, particularly in regard to hydrology and conceptualisation of the hyporheic zone.

This article addresses this gap in the literature by reviewing methods previously used in braided rivers internationally to characterise groundwater–surface water interactions, as well as recommendations for new methods that can be applied in this type of river environment. The objective is to provide guidance for future braided river studies. As described in this section, braided rivers have many features that may make it difficult to apply techniques used in different river environments. While many of these features are found in other river types, they exist in a particular combination in braided rivers, which makes it problematic to investigate groundwater–surface water exchange. The rapidly shifting channels of braided rivers make it difficult to establish, maintain and access study sites. The typical coarse gravel substrate makes it challenging to install instruments in the riverbed. Large braided rivers can be several kilometres wide, resulting in data collection across the width of the river being difficult or impossible. The very permeable gravel streambeds are often highly gaining or losing in respect to groundwater, and these interactions can have large temporal variability. The mixed sand and gravel substrate makes it nearly impossible to take undisturbed samples for sediment structure analysis. The heterogeneous nature of the river substrate and structures – largely mixed sand and gravel, with some clay and silt layers, and open framework gravels – make upscaling point-scale data difficult. A significant portion of river flow occurs within the streambed; and in aquifers, the open framework gravels (i.e. paleo river channels) serve as preferential flow paths. In relation to the methods used in previous studies, this article examines the equipment and study design, cost, issues of temporal and spatial scales, and ultimately the techniques' effectiveness. For general overviews of methodologies not specific to braided river applications, refer to Kalbus et al. (2006); Brodie et al. (2007); Rosenberry and LaBaugh (2008); Lovett (2015); Rosenberry et al. (2015); and Brunner et al. (2017).

2 Methodologies for assessing groundwater–surface water interactions in braided rivers

Various types of methods have been used to investigate groundwater–surface water exchange in braided rivers such as mass balance approaches; hydrochemical tracers; direct measurement of hydraulic properties; and modelling. Many of these studies employed multiple methods to meet their objectives. To thoroughly and clearly assess each method, the techniques, and their advantages and limitations will be discussed individually in the following section, and the discussion section will review the merits and limitations of multi-method studies. This information is then summarised in Sect. 3.

2.1 Water budgets

Some of the most commonly used methods for identifying gains and losses to braided rivers have been based on a mass balance approach. The underlying principle of this method is that any gain or loss of surface water can be related to the water source, and therefore the groundwater component can be identified and quantified (Kalbus et al., 2006). Many of these mass balance approaches have used water budgets to separate groundwater and surface water components both on river-reach and catchment-wide scales.

River-reach water budgets involve estimating the net flux of seepage in a defined river reach by measuring stream discharge in cross sections and then calculating the difference in flow between the cross sections (Kalbus et al., 2006). If there is an increase or decrease in discharge, this can be considered as a gaining or losing reach, respectively, provided any surface inflows or outflows (e.g. tributary inflows, abstractions) are accurately quantified. Measurements should generally be taken in low flow conditions to avoid errors caused by river flow recession after rainfall or snowmelt (Brodie et al., 2007).

Several studies have used river-reach water budgets to identify gaining and losing reaches of braided rivers. The Selwyn River in New Zealand, which has losing and gaining reaches, and annually dries in parts, has been the focus of several studies (Larned et al., 2008, 2015; Vincent, 2005). Both Larned et al. (2008) and Vincent (2005) used flow gauging data to classify gaining and losing reaches of the river. Larned et al. (2015) used a 30-year gauging record from two flow recorder sites on the river to calculate groundwater level lag times. In another study, Farrow (2016) characterised gaining and losing reaches of the four major rivers in the Ashley–Waimakariri zone in New Zealand using historic flow gauge records; however, they cited the need for additional concurrent flow gauging under mean flow conditions to more accurately characterise long-term gaining and losing reaches. In an attempt to determine the causes of the perennial drying of the Ashburton River in New Zealand, Riegler (2012) conducted flow gauging along the river in conjunction with groundwater well measurements, mapping of dry reaches and regression analysis. White et al. (2012) used a steady-state groundwater budget to estimate groundwater outflow from the riverbed based on the mean daily flow at a recorder site on the Waimakariri River and groundwater level observations in a monitoring well array beside the river. The authors found that river channel area rather than channel position was most important in their calculations; however, they recommended that future research examine the effects of channel position and area on groundwater outflow. This is particularly relevant in braided rivers, as their channel positions often change. Both Simonds and Sinclair (2002) and Doering et al. (2013) used flow gauging as part of multi-method studies for estimating groundwater–surface water interactions in the Dungeness River (Washington State, US) and Tagliamento River (northeastern Italy), respectively. These authors conducted concurrent gauging to calculate the net loss or gain of flow along river reaches and compare to data collected from other methods.

A smaller number of braided river studies (e.g. Burbery and Ritson, 2010) have used catchment-scale water budget calculations to estimate the inflow and outflow from braided river catchments and distinguish groundwater from surface water sources. The underlying relationship is provided below (modified from Scanlon et al., 2002):

$$\begin{array}{}\text{(1)}& \mathrm{inflow}=\mathrm{outflow}\pm \mathrm{\Delta }S.\end{array}$$

Here, inflow is the sum of precipitation, surface water inflow and groundwater inflow. Outflow is comprised of actual evapotranspiration, surface water outflow and groundwater outflow. ΔS is the change in water storage in the catchment. This also considers artificial changes to water levels in the catchment such as industrial discharges to surface water or water abstraction. Burbery and Ritson (2010) calculated a water budget for the Orari River catchment in Canterbury, New Zealand, which was based on field observations from various methods including flow gauging and groundwater well observations, climate data, and water use data. The authors used the flow gauging data to classify gaining and losing reaches in four of the rivers in the catchment. They noted that in order to obtain a greater level of detail about groundwater–surface water connectivity at the local scale, shorter-spaced flow gauging coupled with high-resolution piezometric surveys and aquifer pumping tests should be carried out (Burbery and Ritson, 2010).

Advantages and limitations

River-reach water budgets are useful for identifying hotspots of river gains and losses at a broad scale. However, there are several issues regarding their effectiveness in braided rivers. As detailed in Section 1, these types of rivers are typically comprised of heterogeneous materials and thus there may be small-scale interactions of groundwater and surface water within reaches, which flow gauging is poor at identifying (Hughes, 2006). For example, Larned et al. (2015) noted that lag time calculations can only highlight generalised flow paths, whereas predicting more specific groundwater flow paths or residence times would require studies using additional techniques such as tracers or potentiometric data. Also, accurate measurements of flow rates can be compromised by several factors including interference of macrophytes in the streambed, low flow, imprecise or shifting river margins, high sediment load, or unstable streambeds that permit parafluvial flow (i.e. flow in the area of riverbed that is to some extent annually scoured by flooding; Stanford, 2007). As noted by Close et al. (2014), there is significant uncertainty around estimates of river to groundwater flows solely based on hydraulic measurements, particularly for large braided rivers, as these environments provide various challenges for accurate flow measurements. These systems are difficult to measure because precise flow gauging can only be carried out during low flows and measurement errors can be considerable (Close et al., 2014). Often the measurement error is greater than the net exchange of groundwater and surface water (LaBaugh and Rosenberry, 2008).

Catchment water budgets can be a useful method at a larger scale but are generally not appropriate for assessing small-scale groundwater–surface water interactions, as the accuracy of recharge rates to or from rivers is limited by the accuracy of the measurement of the other components in the budget (Scanlon et al., 2002). They can be simple and quick to calculate, but this depends on how time consuming or expensive the data collection is. Also, this method can have low resolution because of the limited number of flow gauging stations on rivers (Kalbus et al., 2006). Thus, when calculating budgets for large catchments, the errors can be significant.

2.2 Hydrochemistry

There are various natural physical and chemical properties of groundwater and surface water that can serve as indications of interaction between the two systems. A variety of tracers have been used in braided rivers to investigate groundwater–surface water exchange including geochemical tracers such as conductivity, chloride or alkalinity; stable isotopes; and radioactive isotopes such as radon. At sites where there is a discernible difference between the groundwater and surface water concentrations of one of these parameters, the influence of groundwater or surface water may be able to be detected. This type of analysis assumes there is an evenly distributed groundwater concentration between sampling locations and that there is complete mixing of water sources (Lovett, 2015). To separate surface water or groundwater components, mixing models based on conservation of mass are used (Kalbus et al., 2006), such as end-member mixing analysis (EMMA) or hydrograph separation. The methods presented below represent the majority of known braided river applications to date, and thus this is not a complete list of all tracers used in previous studies. Some additional tracers applied in braided river settings not discussed in detail here include dissolved oxygen (e.g. Larned et al., 2015; Rodgers et al., 2004), silica (e.g. Botting, 2010; Rodgers et al., 2004; Soulsby et al., 2004), nitrate (e.g. Burbery and Ritson, 2010; Larned et al., 2015; White et al., 2012) and sulfate (e.g. Acuña and Tockner, 2009; Botting, 2010).

2.2.1 Stable isotopes

Oxygen, which is a key component of water, naturally occurs in three stable isotopic forms: mainly as oxygen-16 (¹⁶O), and in smaller proportions as oxygen-17 (¹⁷O) and oxygen-18 (¹⁸O) (Sharp, 2007). Due to the difference in mass between these isotopes, they undergo fractionation during evaporation and condensation (Taylor et al., 1989). The process is largely driven by temperature, humidity and salinity, whereby precipitation is increasingly depleted in ¹⁸O at colder temperatures (which tend to occur at higher elevations) (Sharp, 2007). The ratio of ¹⁶O to ¹⁸O (referred to as δ¹⁸O) is used to identify the relative concentrations of the two most abundant stable oxygen isotopes. This allows for the identification of groundwater recharged by alpine sources and lowland rainfall (Burbery and Ritson, 2010) and can shed light on groundwater flow paths in aquifers.

Several studies have used δ¹⁸O to characterise groundwater–surface water exchange in braided rivers and their associated aquifers. Blackstock (2011) found their isotopic model for the Christchurch, New Zealand, groundwater system matched well with previous physical mass balance calculations and that stable isotope analysis was useful, especially in shallow groundwater. Botting (2010) found that stable isotope analysis was the most effective technique for distinguishing surface water from groundwater amongst the multiple methods that they used (including hydrochemical sampling, pumping tests, and groundwater well observations) in a study of the north bank of the braided Wairau River in New Zealand. In addition, Vincent (2005) successfully used δ¹⁸O analysis to identify groundwater recharge sources in the upper Selwyn River catchment. Burbery and Ritson (2010) used δ¹⁸O analysis to determine alpine versus lowland recharge sources for groundwater in the Orari River catchment. Of the various methods used in the study (which also included flow gauging, a catchment-scale water budget, chemical tracers and groundwater level observations), the authors found δ¹⁸O analysis to be highly effective for understanding groundwater–surface water interactions in the catchment. Given δ¹⁸O varies seasonally, they recommended sampling be carried out at various times during the year to obtain better temporal resolution, as well as on a long-term basis to consider climatic variations. Hanson and Abraham (2009) carried out δ¹⁸O and other hydrochemical analyses along two transects across New Zealand's Canterbury Plains. The authors found δ¹⁸O to be the most reliable tracer to differentiate between land surface recharge and alpine river water. However, they pointed out that a suite of tracers would be needed to characterise groundwater flow paths and groundwater recharge sources. They also noted that δ¹⁸O can be significantly altered where alpine water is used for irrigation.

2.2.2 Radon

Radon-222 (Rn-222) is another useful tracer for identifying groundwater–surface water interactions. It is a chemically and biologically inert radioactive gas part of the uranium-238 decay process and is present in nearly all rocks and soils (LaBaugh and Rosenberry, 2008). As water flows through rocks and soils it becomes enriched in Rn-222. In surface waters, radon quickly degasses, so groundwater generally has Rn-222 concentrations 3 to 4 orders of magnitude higher than surface waters, thus making it an effective tracer in many environments (Burnett et al., 2001). For example, an area of high radon concentrations in surface water would suggest groundwater inflow. It is a cost-effective, simple technique that is suitable for study areas ranging in size (Martindale, 2015).

Rn-222 analysis can address many questions related to groundwater and surface water interactions. In a multi-method study in the braided Tagliamento River in northeastern Italy, Acuña and Tockner (2009) used Rn-222 to assess the residence time of upwelling groundwater in the hyporheic zone. Moore (1997) analysed Rn-222 to estimate groundwater inflow to the Brahmaputra River in the Bay of Bengal. Close et al. (2014) used Rn-222 sampling to calculate the velocity of groundwater recharge from the Waimakariri River to groundwater in the Canterbury Plains in New Zealand using the ingrowth (i.e. the rate of build-up in a closed system) equation for Rn-222. The authors recommended that a high-resolution study with closely spaced sampling sites could be useful for highlighting preferential flow paths in the riparian zone. In addition, Close (2014) sampled Rn-222 amongst other hydrochemical parameters in the Wairau River in Marlborough and in groundwater wells within 5 km of the river to better understand the groundwater–surface water interactions in the river and the amount and variability of recharge to the groundwater system. Close (2014) found that temperature correlated well with the spatial distribution of the radon but added that there could be significant errors with estimating groundwater flow paths due to local heterogeneity and the meandering nature of the alluvial deposition process in the area. Close (2014) recommended analysing temperature and data collected from piezometers in conjunction with radon to resolve these uncertainties.

There are some limitations of Rn-222 analysis, as it requires several assumptions, including that stream water is well mixed downstream of groundwater discharge areas, water fluxes are constant, the radon activity in the stream water and groundwater are known and constant, and there is no additional surface recharge from sources such as streams or stock water races (Kraemer and Genereux, 1998). It also may be difficult to distinguish between regional groundwater discharge and hyporheic zone exchange using radon analysis (Lovett, 2015; Martindale, 2015). Rn-222 concentrations will also vary with different mineral compositions in the rocks present (Close et al., 2014).

2.2.3 Chloride

The chloride ion (Cl⁻) can be used as an indicator for groundwater and surface water mixing in locations with sufficiently distinct chloride concentrations in groundwater and surface waters. For example, the groundwater surrounding the Bow River in the Canadian province of Alberta has elevated levels of chloride from road salting. This allowed Cantafio and Ryan (2014) to measure chloride levels in an urban reach of the river and assess water quality impacts and baseflow sources. They found that nearly all river flow originates in the Rocky Mountains and there is little contribution from groundwater.

Chloride is frequently sampled amongst a suite of hydrochemical parameters to investigate groundwater and surface water interactions, as groundwater often becomes enriched in chloride as it passes through soil and rocks (Dommisse, 2006). Burbery and Ritson (2010) measured chloride concentrations in the Orari River catchment in New Zealand, specifically looking at chloride-to-sulfate ratios to delineate groundwater–surface water interactions and examine recharge sources in the catchment. They found that basic ion chemistry was useful for determining the extent of the Orari River water but noted that results can be complicated by hydrochemical changes due to land use activities. Several other studies measured chloride to determine recharge sources and quantities in braided rivers and their associated aquifers including Acuña and Tockner (2009), Larned et al. (2015), Botting (2010) and Domisse (2006).

2.2.4 Alkalinity

Alkalinity can serve as an effective indicator for determining catchment water sources. In a study of the braided River Feshie, in the Cairngorms in Scotland, Rodgers et al. (2004) used alkalinity as a tracer to investigate temporal changes in stream water hydrochemistry and characterise sources of river flow. The authors noted that Gran alkalinity is particularly useful as it serves as a directly measurable, close approximation to the acid neutralising capacity, which is considered a conservative chemical tracer. Gran plots are commonly used to determine alkalinity and acid neutralising capacity in water with low alkalinity or low conductivity. A Gran function plot identifies the point at which all alkalinity has been titrated in a strong-acid–strong-base titration (Rounds and Wilde, 2002). Rodgers et al. (2004) used EMMA to estimate different hydrological sources of River Feshie water. The authors were reasonably confident of their estimates because of the extensive temporal and spatial components of their study. Because of the relative simplicity and low cost of the Gran alkalinity method, these types of longer-term and detailed spatial surveys are becoming increasingly feasible (Rodgers et al., 2004), though may be costly in terms of human resources required. In another study in the Feshie catchment, Soulsby et al. (2004) conducted a geochemical tracer study to improve large-scale flow path understanding. The authors carried out chemical-based hydrograph separations to separate baseflow from storm event sources. They analysed for Gran alkalinity, which they noted was simple and inexpensive to measure. Alkalinity has proven to be a useful parameter in the United Kingdom (UK) to distinguish between water sourced from acidic, organic soils (which are common in the UK at shallow depths) and deep, older groundwater. Soulsby et al. (2004) found their study provided valuable information at the sub-catchment scale, but more information was needed at finer spatial scales.

Advantages and limitations

Hydrochemistry can provide significant insight into catchment-wide hydrology, as well as provide estimations of seepage flux on the point scale (Close, 2014; Dommisse, 2006; Lovett, 2015). Even considering catchment heterogeneity, some tracers can behave predictably enough to serve as effective tracers for studies of braided rivers (Soulsby et al., 2004). Environmental tracers are useful in settings where there is a sufficient difference between tracer concentrations in the groundwater and surface water, and some parameters can be easily incorporated in long-term routine monitoring programs. Disadvantages of these methods include that hydrochemistry of the baseflow and storm event water composition may be too similar, or that hydrochemistry may not be constant in time or space (Genereux and Hooper, 1998). Importantly, various tracers such as dissolved oxygen, pH, nitrate and sulfate may be affected by biogeochemical processes, so to be effective, the tracers must be conservative at the scale of the investigation. Also, land use activities may alter hydrochemistry in catchments, for example from fertiliser application or mixing of water sources through irrigation (Soulsby et al., 2004). Additionally, some low tracer concentrations may cause analysis errors (e.g. in the case of radon) (Close, 2014).

2.3 Temperature studies

Temperature has been used in a number of studies to characterise groundwater–surface water interactions in braided rivers. In most locations, during winter and summer months, there is a discernible difference in groundwater and surface water temperatures. In general, groundwater temperature is more stable, whereas surface water temperatures change diurnally and seasonally (Kalbus et al., 2006). In summer, groundwater is typically colder than surface water, whereas in winter, groundwater is generally warmer. Heat tracer methods can be used to identify discharge and recharge zones as well as quantify the flux of water moving between groundwater and surface water systems (Andersen, 2005). There are various methods involving temperature sensing that range in complexity, scale and cost. One-off temperature readings can be taken using probes, or sensors and data loggers can gather time-series data either in-stream or in groundwater wells. Vertical and horizontal temperature profiles can also be measured by arranging sensors in a series either in-stream or in wells on river margins. Temperature profiles can be analysed using various methods such as VFLUX (Gordon et al., 2012) or the steady-state approach (Schmidt et al., 2006). Some temperature methods, such as thermal infrared imaging and fibre-optic temperature sensing (both of which are discussed further in Sect. 4), are best suited for identifying patterns, such as temperature differences in surface water that may indicate areas of recharge or discharge. Other methods such as temperature depth profiles can be used to quantify the flux of water through the streambed.

The following studies demonstrate various applications of temperature measurement that have been used to characterise groundwater–surface water exchange in braided rivers. Passadore et al. (2015) conducted thermal monitoring to characterise the temporal and spatial variability of streambed water fluxes in the Brenta River in Italy. They used heat as a tracer in conjunction with water level measurements and found this combination of methods to be effective in estimating groundwater–surface water interactions. Two studies of the Wairau River in Marlborough, New Zealand, analysed temperature (Close, 2014; Close et al., 2016). Close (2014) measured temperature in the river and in groundwater wells located near the river to characterise river recharge to the aquifer. The author compared the data to Rn-222 analysis and found that the temperatures correlated well with the spatial distribution of radon. Close et al. (2016) used the daily mean temperatures in groundwater wells to estimate the lag time between the river and the observation wells. Lastly, Coluccio (2018) used VFLUX to analyse diurnal temperature signals to characterise seepage through the streambed of a braided river. The study determined the direction and magnitude of vertical seepage through the streambed using temperature probes in the Ashburton River in New Zealand. The results were compared with hydrochemistry and water level measurements in the river and shallow groundwater to better inform the interpretation of the temperature data. Coluccio (2018) found that it was difficult to distinguish between shallow groundwater and hyporheic flow and also noted that further studies would benefit from combining a point-scale method like temperature probe analysis with broader-scale techniques.

Advantages and limitations

Heat tracers offer many techniques at varying spatial and temporal scales. Broad-scale methods like aerial thermal infrared imaging can be used to obtain large-scale data, and they can offer the advantage of remote collection of data in areas that are difficult to access. Point-scale techniques using temperature sensors can indicate surface water-groundwater interactions at a specific location. Some methods of temperature analysis can also quantify seepage flux (e.g. using diurnal signal analysis). The methods range in cost and complexity, and thus can be tailored to suit a study's needs. There are some limitations including that a temperature gradient between groundwater and surface water might not always be present (e.g. this may be affected by environmental conditions such as season, wind, shade from vegetation or rapidly changing river levels) (Johnson, 2003). Also, for certain types of analysis, temperature needs to be measured continuously (Irvine et al., 2017). In addition, due to the dynamic nature of braided rivers and their associated sediments, heat transfer within the heterogeneous materials may be non-linear.

2.4 Darcy approach

2.4.1 Hydraulic gradient

Groundwater levels are often used to aid in the understanding of groundwater–surface water interactions, and there have been several studies conducted in braided rivers using this technique. Groundwater level data can be used to identify the hydraulic gradient (i.e. the difference in hydraulic head over a given distance) at a location, which can reveal groundwater discharge to a river or river recharge into an aquifer. The underlying principle is that if groundwater levels in a well are higher than the river level, the river is gaining (i.e. groundwater is flowing into the river). Conversely, where river levels are higher than the groundwater level in a nearby well, the river is losing (i.e. river water is flowing into groundwater). It is worthwhile to note that it is important to obtain a conceptual understanding of the relationship of the river to the water table, as the river might be connected, disconnected or in a transitional state between the two (Brunner et al., 2009). Groundwater levels are most typically measured using pressure transducers or electronic water level indicators.

The hydraulic gradient is calculated as Δh∕Δl, where Δh [L] is the difference in hydraulic head [L] and Δl is the distance between the points where the hydraulic head was measured. Hydraulic gradient can be measured in the horizontal direction to characterise flows into or out of a river through the sides of the river. Here, Δh [L] is the difference between the groundwater level in a well at the edge of the river and a well a distance Δl [L] away from the edge of the river. Hydraulic gradient can also be measured in the vertical direction to characterise vertical flows into or out of the river through the streambed. In this case, Δh [L] is the difference between the groundwater level in an in-river piezometer and the river level at that location; and Δl [L] is the distance from the riverbed to the top of the well screen (Doering et al., 2013).

Once the hydraulic gradient has been measured, the magnitude of groundwater flow into or out of a river can be estimated using the Darcy equation:

$$\begin{array}{}\text{(2)}& Q=-KA{\displaystyle \frac{\mathrm{\Delta }h}{\mathrm{\Delta }l}},\end{array}$$

where Q [L³ T⁻¹] is the volume of flow, A [L²] is the cross-sectional area perpendicular to flow through which the water passes, and K [L T⁻¹] is hydraulic conductivity (Schwartz and Zhang, 2003). For calculating the horizontal flow magnitude, a horizontal hydraulic conductivity of the surrounding aquifer is generally used. To calculate the vertical magnitude of flow, the vertical hydraulic conductivity of the streambed needs to be determined, as does the streambed area over which the water exchange occurs (Simonds and Sinclair, 2002).

In terms of specific methods that can be used for measurements, existing piezometers (i.e. monitoring wells) near rivers can be useful for conducting these types of studies, particularly given the often high cost of drilling new wells. Please refer to a standard text such as Fetter (2001) for a definition of piezometers. Mini-piezometers, which are scaled-down versions of piezometers and typically installed no deeper than about 2 m (Figs. 4 and 5), have been previously used in studies of braided rivers (Acuña and Tockner, 2009; Doering et al., 2013; Malard et al., 2001). We recommend referring to the studies mentioned in this section for piezometer designs for braided river applications, as feasibility of installation into coarse gravel is one of the significant limitations of this technique, and not all designs would be effective in braided rivers for this reason.

Figure 4 Conceptual diagram of a mini-piezometer (Coluccio, 2018).

Figure 5 Mini-piezometer installed on the bank of a braided river (Coluccio, 2018).

Previous studies have examined the correlations between groundwater levels and river levels to establish the degree of connectedness of groundwater systems and braided rivers, for example, attempting to identify the causes of drying reaches and changes in long-term river flows. Prior studies have been carried out in catchments with substantial agricultural surface and/or groundwater abstraction for irrigation. Thus, the questions here are often whether abstraction has caused drying in rivers or decreases in river flows, and what effect future abstraction will have. These studies have often coupled groundwater level measurements with streamflow gauging and physicochemical sampling of river water and groundwater. Riegler (2012) examined groundwater levels, in conjunction with flow gauging, in the North Branch of the Ashburton River in Canterbury, New Zealand, to attempt to correlate groundwater levels and decreased flow levels in the river. The study concluded that there were too many uncertainties, particularly around the complex behaviour of the groundwater system, to draw strong conclusions on the causes of the drying riverbed. Several other studies also investigated New Zealand braided rivers that are highly connected to groundwater using these methods (Larned et al., 2008, 2015; Vincent, 2005; Coluccio, 2018).

A multi-method study was carried out on the Dungeness River in Washington State in the US to characterise groundwater–surface water interactions. Simonds and Sinclair (2002) installed mini-piezometers in the river in which they measured the vertical hydraulic gradient between the stream and water table. They also continuously monitored water levels and temperature in two well transects, providing data on the horizontal hydraulic gradient and temporal changes in groundwater–surface water flows. The authors also conducted flow gauging along “seepage runs” in the river to quantify the net gain or loss of flow over a reach.

Groundwater level measurements in mini-piezometers have also been applied in studies of European braided rivers. Malard et al. (2001) calculated the difference in hydraulic head between hyporheic water and surface water and between the parafluvial hyporheic zone and the river using mini-piezometers in the Roseg River in Switzerland. Acuña and Tockner (2009) also incorporated groundwater level observations into their multi-method study of the Tagliamento River in Italy. The used PVC mini-piezometers installed to a depth of 50 cm in four reaches of the river. They calculated vertical hydraulic gradient to determine the direction and intensity of surface and subsurface (i.e. hyporheic flow or groundwater) exchange in the streambed. In another study of the Tagliamento River, Doering et al. (2013) installed mini-piezometers along 10 transects in losing and gaining reaches of the river. Five mini-piezometers were installed horizontally across the river at each location and were used to calculate the vertical hydraulic gradient where the piezometers were installed.

2.4.2 Hydraulic conductivity

As detailed above, the hydraulic conductivity of riverbeds is needed to calculate the magnitude of flow through the riverbed. There have been a number of studies investigating the hydraulic conductivity of streambeds (e.g. Landon et al., 2001; Kelly and Murdoch, 2003), though few studies have been conducted in braided rivers. There are many well-established methods for calculating hydraulic conductivity of a porous medium, including grain size analysis, permeameter tests, slug and bail tests, and pumping tests (see Fetter, 2001).

In an early investigation of the permeability of gravel streambeds, Van't Woudt and Nicolle (1978) extracted gravel from the bed of the braided Waimakariri River in Canterbury, New Zealand. They conducted lab-based tests to determine hydraulic properties of the bed substrate such as porosity and infiltration rates. This study resulted in several conclusions about subsurface flow in gravel-bed rivers, including that fine sediments flowing through the gravels tend to create a low-permeability clogging layer along the margin of and below the riverbed. The authors also found horizontal permeability to be far higher than vertical permeability (30:1), but it is difficult, if not impossible, to draw conclusions about horizontal and vertical conductivities once the sediment is disturbed.

Cheng et al. (2010) carried out a study to determine the statistical distribution of streambed vertical hydraulic conductivity at 18 sites along a 300 km reach of the Platte River in Nebraska. They conducted in situ permeameter tests using falling head tests and found that vertical hydraulic conductivity was normally distributed at all but one of their study sites.

In a study on the north bank of the Wairau River in Marlborough, New Zealand, Botting (2010) conducted pumping tests to determine groundwater flow paths and origins. The pumping tests were of limited use, however, because the pumping did not successfully lower the groundwater levels, most likely due to the high transmissivity of the aquifer.

On the Ashburton River in New Zealand, Coluccio (2018) conducted slug tests in mini-piezometers installed on the margins of the river. The hydraulic conductivity values calculated from the slug tests were on the low end of the range for expected hydraulic conductivity values in this area, which may have been a reflection of the tests being conducted in localised areas of finer sediments, highlighting the limits of using this point-scale method in heterogeneous environments (Coluccio, 2018).

Advantages and limitations

There are various benefits and drawbacks of the methods described in this section. The use of existing groundwater wells may be very convenient in a study, but the installation of new deep wells generally comes at a high cost. Mini-piezometers offer an inexpensive and simple method for obtaining groundwater level and pressure data (Lee and Cherry, 1978). They are easy and quick to install in most locations, and the analysis of their measurements is generally straightforward (Brodie et al., 2007). They can be used in small-scale applications and in detailed surveys in heterogeneous environments (Fritz et al., 2016). However, measurements at a study site must be taken at the same time to be representative of similar flow conditions (Kalbus et al., 2006). Another important factor to consider is that many data loggers require a certain diameter well. In previous studies, groundwater level observations have rarely been used in isolation and typically have been coupled with other methods.

The heterogeneous composition of braided rivers complicates the estimation of the hydraulic conductivity of streambeds on a reach or catchment scale. Hydraulic conductivity can vary significantly across an area, even with small changes in sediment composition, and thus it is difficult to extrapolate values to represent a large area (Brodie et al., 2007). With grain size analysis, the structure and stratification of the sediment are destroyed during analysis, so the conductivity value does not represent the vertical or horizontal conductivity (Cheng and Chen, 2007) and does not provide any information on preferential pathways (Brunner et al., 2017). This issue is particularly problematic in gravel-bed braided rivers where there is high anisotropy and a large portion of subsurface flow occurs in preferential channels (Dann et al., 2008). Similarly, when conducting permeameter tests it is difficult to transport sediment samples without disturbing their structure (Kalbus et al., 2006). In particular, taking undisturbed cores of sediments containing unconsolidated gravel, as most braided rivers do, is nearly impossible. However, these tests can be used as a preliminary estimation before conducting further tests. Also, there is the potential for freeze coring, which allows for an intact sediment sample, but there are limitations, such as in rivers with warm water or compacted cobbles (Brunner et al., 2017). Slug tests are quick and simple to carry out and a significant advantage is that they only require one well. Pumping tests on the other hand require a pumping well and an observation well, which can be cost prohibitive. Pumping test results provide average hydraulic conductivity values across a larger area than for slug tests, and thus their results may be less sensitive to heterogeneous conditions (Kalbus et al., 2006), whereas slug tests provide information only about the location where the well is installed. Arguably, as vertical hydraulic conductivity is the controlling factor for river losses, there should be more focus on estimating anisotropy values of the braided river substrate. Methods for estimating anisotropy have been demonstrated using aquifer tests (Neuman et al., 1984; Mutch, 2005; Mathias and Butler, 2007) and more recently geophysics (Al-Hazaimay et al., 2016; Fernández-Álvarez et al., 2016).

2.5 Modelling

Computer modelling is often used for the estimation of exchange between surface water and groundwater as a complement to field measurements. Such computer models have become irreplaceable tools to gain insight into real-world surface water-groundwater issues ranging from system understanding at the local or regional scale to future projections for management purposes. The complexity of numerical hydrological models used for this purpose range from simple conceptual models that treat subsurface compartments (i.e. groundwater) as reservoirs where inflows or outflows are specified, to highly complex integrated models that have a more realistic physical coupling between surface water and groundwater. MODFLOW (Harbaugh, 2005) is the most commonly used numerical model to simulate surface water-groundwater interactions (Furman, 2008; Barlow and Harbaugh, 2006). As pointed out by Wohling et al. (2018), MODFLOW is considered to be a good compromise between integrated and conceptual modelling approaches. Several packages are available in MODFLOW for simulating surface water-groundwater interaction and further details about the application and limitations of these can be found in Brunner et al. (2009, 2010).

While the modelling of braided rivers is not new, it has been done more often from a geomorphological perspective (e.g. Ashmore, 1993; Copley and Moore, 1993; Meunier et al., 2006; Williams et al., 2016). Nevertheless, a number of published studies detail modelling of braided rivers for the purposes of understanding groundwater–surface water interactions (e.g. Baalousha, 2012; Chen, 2007; Passadore et al., 2015; Scott and Thorley, 2009; Shu and Chen, 2002; Wilson and Wohling, 2015; Wohling et al., 2018).

Wilson and Wohling (2015) attempted to improve the understanding of Wairau River recharge into the Wairau aquifer in Marlborough, New Zealand, using a steady-state MODFLOW model and the SFR2 package. The authors noted groundwater monitoring records and pump testing showed the aquifer to be more complex and stratified than previously thought, indicating that groundwater monitoring sites were likely only representative of local conditions. This finding underscores the difficulties of modelling highly heterogeneous, complex river systems and their associated aquifers. This was further highlighted by Close et al. (2016), who used the Wilson and Wohling (2015) MODFLOW model as a basis for a study using heat as a tracer in the Wairau aquifer. Close et al. (2016) found that including heterogeneity was important when calibrating the model to observed temperature data.

In a subsequent study of the Wairau Plain aquifer and the Wairau River, Wohling et al. (2018) developed a transient MODFLOW model that was calibrated using targeted field observations as well as “soft” information from experts of the local water authority. The uncertainty of simulated river-aquifer exchange flows was evaluated using null space Monte Carlo methods. The study suggested that the river is hydraulically perched (losing) above the regional water table in its upper reaches and is gaining in the downstream section. It was found that despite large river discharge rates (i.e. regularly reaching 1000 m³ s⁻¹), the net exchange of flow rarely exceeded 12 m³ s⁻¹ and seemed to be limited by the physical constraints of unit-gradient flux under disconnected rivers. An important finding for the management of the aquifer was that changes in aquifer storage are mainly affected by the frequency and duration of low-flow periods in the river.

Advantages and limitations

Field methods are often time consuming and expensive, and they may not be at the targeted spatial or temporal scale. Therefore, the estimation of exchange between braided rivers and groundwater is often complemented by hydrological modelling. It is also possible to integrate a range of data types at varying spatial and temporal scales with modelling. MODFLOW is commonly used to model surface water-groundwater interaction, including in braided rivers. Complex flow channel geometry, which changes over time, is not explicitly incorporated into modelling efforts, at least in the studies identified by the authors listed above. As such, the impact of complex and temporally variable flow channel geometry on surface water-groundwater exchange is not well understood. More complex integrated modelling approaches than that possible using the MODFLOW suite of packages is likely required to incorporate this level of detail. A future integrated approach that considers channel geometry in a more physically realistic manner may be facilitated by the recent development of braided river terrain models (e.g. Williams et al., 2016) and methods for simulating the heterogeneity of braided river sediments (e.g. Ramanathan et al., 2010).

3 Discussion

There are many factors to consider when selecting the appropriate method(s) for studying groundwater–surface water interactions, and there are special considerations relevant to braided river environments. The most appropriate method will depend on physical and hydrological conditions in the setting and scale of interaction to be measured (LaBaugh and Rosenberry, 2008). As a result of this review of studies investigating groundwater–surface water exchange in braided rivers, a summary table has been developed (Table 1) that summarises the literature discussed in this paper and the advantages and disadvantages of the various methods used in these studies.

Table 1 Advantages and disadvantages of various methodologies for measuring groundwater–surface water interactions in braided rivers.

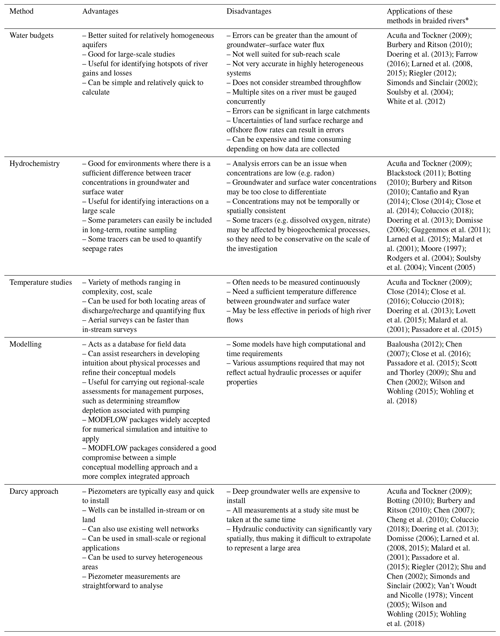
^* Note: some studies referenced in this table were not discussed in the text.

The objectives of a study will influence which methods are most applicable. If only qualitative information about groundwater–surface water exchange is required, this could be obtained by methods such as mapping the locations of wet and dry reaches of a river, or identifying where there is mixing between groundwater and surface water based on chemical or heat tracers. Qualitative data will often assist in developing a conceptual understanding of the study site, which is a critical first step in data gathering. Alternatively, if quantitative data are needed, such as the rate of groundwater seepage into a surface water body, this may be obtained by measuring Rn-222, analysing temperature signals, or by calculating the hydraulic gradient. Researchers have developed flux quantification techniques for some of the methods discussed in this paper (e.g. for temperature analysis see Gordon et al., 2012), but it is important to consider inputs required to calculate seepage through a streambed, such as streambed hydraulic conductivity (see Sect. 2.4). If direct water samples are needed, tools to consider could include groundwater wells or mini-piezometers. Water samples and flux rates can also be obtained using seepage meters, a common method used for estimating groundwater–surface water interactions typically based on the design proposed by Lee (1977). However, it does not appear that these devices have been previously used in gravel-bed braided rivers. Seepage meters have various limitations as discussed in previous studies (e.g. Kelly and Murdoch, 2003; Brodie et al., 2009; Cey et al., 1998), which indicate their application in braided rivers would be difficult and less effective than other methods.

It is important to match the scale of the data required with the methods being used. This should include the consideration of both spatial and temporal scales. Remote sensing techniques such as airborne thermal infrared imaging and geophysics may prove useful to apply in braided river settings for gathering data on a large scale, as these methods have been used in braided rivers for geomorphological studies (e.g. Huber and Huggenberger, 2016) and for investigating groundwater–surface water exchange in other settings (McLachlan et al., 2017). We discuss these approaches further in Sect. 4. It is important to recognise that it may be difficult to accurately characterise smaller-scale groundwater–surface water interactions in highly heterogeneous braided river environments based on broad-scale methods. However, obtaining a broad snapshot of conditions or processes in a location may provide sufficient information to satisfy the study's objectives. Also, using a combination of broad and point-scale techniques at a single study site may help overcome the limitations of the individual techniques, particularly in heterogeneous environments (Kalbus et al., 2006).

Site-specific characteristics will largely determine the most appropriate methods to use relating to the geology, topography, hydrochemistry, hydrology and hydrogeology of the study site. Large braided rivers with high flows and deep channels may prove difficult to access directly. There is also a reasonable risk of the loss or damage of equipment installed in braided riverbeds due to floodwaters and sediment movement. These practical considerations underline the potential benefits of remote techniques to collect data in this type of river.

4 Key gaps and possibilities

This paper has highlighted that there are currently gaps in the knowledge of how groundwater and surface water interact in braided rivers. There is limited conceptual understanding of hyporheic flow processes, and how they impact river flow levels and water quality in braided rivers. The hyporheic zone has been highlighted as a significant area for ecological processes in rivers (Febria et al., 2011; Krause et al., 2011; Malard et al., 2001), but as Kalbus et al. (2006) note, it can be difficult to differentiate between hyporheic exchange and groundwater discharge. In addition, despite the contributions of the studies discussed here, the recharge rates to and from braided rivers continue to be an open question for water scientists and managers, as this has implications for both water quality and quantity. Measuring seepage rates is still difficult in many gravel-bed braided rivers, and often there is significant uncertainty in the data collected. Lastly, there is still much scope for research on identifying historical patterns of dry and low-flow periods in braided river reaches. This is often an area of significant concern for communities that are seeking answers on the correlations between dry or low-flow periods, and current and historical water use practices and climate.

There is also room for improvement in the methods available to carry out these investigations. Refinement of techniques that allow for direct measurements of physical or chemical properties in braided rivers would be helpful. While the studies presented here have employed some direct methods, there is still a need for techniques that can be used in braided rivers with coarse gravel substrate, wide active riverbeds, and shifting channels and gravel bars. Methods that can better capture the heterogeneous properties of braided rivers would be ideal. The present paper has shown the promise of using environmental tracers such as Rn-222 and stable isotopes, as well as heat tracers in these settings. Additional techniques that allow for indirect measurements would also be beneficial, given the difficulty of working directly in braided rivers. Geophysical methods (discussed in more detail below) have been used in many other river environments to gather information about hydrogeologic systems that can then be inferred to better conceptually understand groundwater–surface water exchange. There is also scope for more remote collection of data, and Carbonneau and Piégay (2012) review a range of techniques for use in rivers, while Marcus (2012) provides an overview of remote sensing specifically in gravel-bed rivers. There is a significant amount of freely available satellite data (e.g. via the Sentinel satellites, https://sentinel.esa.int/web/sentinel/home, last access: 22 October 2019) that may be useful in braided river studies. Unmanned aerial vehicles have become more affordable and advanced in recent years, allowing for remote collection of a range of data on rivers such as thermal infrared, multispectral and hyperspectral imaging, and photogrammetry (Pai et al., 2017).

Artificial dye, chemical (e.g. salt) or bacterial tracers are often useful for shedding light on processes such as groundwater velocity and flow paths or hyporheic zone flow (Flury and Wai, 2003). They have been used in other types of rivers to investigate groundwater–surface water exchange (e.g. Binley et al., 2013; Ferreira et al., 2018; Stoner et al., 2013; Knöll and Scheytt, 2018; González-Pinzón et al., 2015). Several studies have used rhodamine dye in a New Zealand well array installed in an alluvial aquifer deposited by braided rivers to estimate hydraulic properties and examine groundwater flow paths (e.g. Close et al., 2002; Dann et al., 2008; Sarris et al., 2018). For artificial tracer tests to be time and cost effective, some prior knowledge of water flow paths and velocities is necessary (Close et al., 2002).

There is scope to use other temperature methods than those described in Sect. 2.3, such as fibre-optic distributed temperature sensing (FODTS) (Busato et al., 2019; Klinkenberg, 2015; Lovett et al., 2015; Meijer, 2015; Rosenberry et al., 2016; Mwakanyamale et al., 2012) or active heat pulse methods (see Briggs et al., 2016; Banks et al., 2018). Collection of temperature profiles was briefly mentioned in Sect. 2.3 in the study conducted by Coluccio (2018), which used 1-D temperature profiles. However, there are several ways temperature profiles can be collected (1-D, 2-D, 3-D), as well as a range of analysis methods that can be used, as demonstrated in several previous studies in non-braided river settings (Briggs et al., 2014; Gordon et al., 2013; Naranjo and Turcotte, 2015; Rosenberry et al., 2016). There is also considerable scope for applying thermal infrared (TIR) imaging in braided rivers. Handcock et al. (2012) provide a comprehensive review of the use of TIR imaging in rivers. Using TIR imaging to highlight temperature differences in a braided streambed may be particularly useful for qualitatively identifying locations of groundwater inflow to rivers. TIR data can be collected remotely (by UAV, helicopter or fixed-wing plane), on the ground or by satellite, and there are important considerations with each category (e.g. cost, scale of data collected). TIR imaging has been used in several river environments to identify groundwater–surface water interactions (Culbertson et al., 2013; Eschbach et al., 2017; Hare et al., 2015; Liu et al., 2016; Lovett et al., 2015; Rautio et al., 2018) but does not appear to have been applied in braided rivers to any great extent for this purpose.

There have been many advances in geophysical techniques in recent years, and these methods do not appear to have been applied in braided river settings for investigations of groundwater–surface water exchange. McLachlan et al. (2017) provide a thorough recent review of geophysical methods for characterising the groundwater–surface water interface, such as electrical resistivity tomography (ERT), ground penetrating radar (GPR), seismic methods, and forward and inverse geophysical modelling. These methods allow for river systems to be characterised where factors such as geological, hydrological and biogeochemical heterogeneity make it difficult to make direct measurements (McLachlan et al., 2017). Geophysical methods may be particularly useful for characterising subsurface structures in braided rivers, which are poorly understood. A recent study by Busato et al. (2019) demonstrates the use of ERT and FODTS in a rocky stream with poorly sorted substrate, the results of which may provide useful insight for braided river applications. Examples of studies in other types of river environments that used geophysics to characterise the groundwater–surface water interface include Singha et al. (2008), Binley et al. (2013) and Steelman et al. (2017). Geophysical data can also be collected remotely in airborne electromagnetic surveys such as in Harrington et al. (2014). As McLachlan et al. (2017) note, geophysical techniques should be used to complement data collected by other hydrological and biogeochemical methods.

As discussed in the modelling section of this paper, there is also opportunity for new approaches to modelling of braided rivers. Brunner et al. (2017) note that there have been recent advances in hydrologic modelling that incorporate both surface and subsurface water flow, and there is certainly room to apply some of these techniques to braided river settings. Given the dynamic nature of braided river subsurface hydrology, models needed to fully couple surface and subsurface flow. There are software packages that have been applied elsewhere such as HydroGeoSphere (e.g. Gilfedder et al., 2019; Goderniaux et al., 2009; Tang et al., 2017) and MIKE-SHE (e.g. Butts et al., 2019; House et al., 2016; Bandini et al., 2017) that appear promising to try in addition to MODFLOW, which has been traditionally used in braided river modelling of the groundwater–surface water interface. As the braided river bedform cannot be sufficiently characterised using the existing MODFLOW SFR functions, there is a need to address this gap. Also, current groundwater models do not allow for changes to bed morphology, which is a key feature of braided rivers, but using script-based models (e.g. FloPy; Bakker et al., 2016) may allow for this to be achieved.

5 Summary

Braided rivers are unique and dynamic river environments that perform important ecological, cultural, recreational and freshwater resource functions. A critical aspect of their effective management is understanding groundwater and surface water interactions in these rivers and their associated aquifers. This article provides an overview of characteristics specific to braided rivers, which include multiple meandering channels that often shift, temporary and semi-permanent bars and islands, wide active riverbed areas, heterogeneous and (typically) mixed sand and gravel streambeds, and a significant portion of river flow that occurs within the streambed. We present a map showing the regions where braided rivers are mainly found at the global scale: Alaska, Canada, the Japanese and European Alps, the Himalayas, Russia, and New Zealand. To the authors' knowledge, this is the first map of its kind. Our review of prior studies of surface water-groundwater interactions in braided rivers showed that most studies have been recent (in the past 10–20 years), and they have investigated a range of questions including calculating seepage rates to and from braided rivers, estimating time lags between rivers and groundwater, and looking at the implications of groundwater–surface water exchange on ecological processes. We also investigated the effectiveness of the various methods used in the studies identified in this review in terms of achieving the studies' objectives and their applicability in braided rivers. A table has been produced summarising these findings and shows that there is a variety of available methods ranging in cost and scale.

Lastly, this article explored the various considerations one may make when choosing appropriate techniques for investigating groundwater–surface water exchange in braided rivers. The use of multiple methods at varying spatial scales at a single study site may help overcome the uncertainties associated with data gathered in heterogeneous, dynamic braided river environments. Given the challenges of working directly in braided rivers, there is considerable scope for the increased use of remote sensing techniques and geophysics. There is also scope for new approaches to modelling braided rivers using integrated techniques that incorporate the often-complex river bed terrain and geomorphology of braided rivers explicitly. There is presently limited understanding of how hyporheic zone processes operate and impact braided rivers, recharge rates to and from braided rivers, and historic drying and low-flow trends in braided rivers, and thus future research is needed in these areas. While only some of the methods discussed here allow for quantification of groundwater–surface water flux, many of these techniques can improve our conceptual understanding of these systems and processes.