the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantitative precipitation estimation with weather radar using a data- and information-based approach
Malte Neuper
In this study we propose and demonstrate a data-driven approach in an “information-theoretic” framework to quantitatively estimate precipitation. In this context, predictive relations are expressed by empirical discrete probability distributions directly derived from data instead of fitting and applying deterministic functions, as is standard operational practice. Applying a probabilistic relation has the benefit of providing joint statements about rain rate and the related estimation uncertainty. The information-theoretic framework furthermore allows for the integration of any kind of data considered useful and explicitly considers the uncertain nature of quantitative precipitation estimation (QPE). With this framework we investigate the information gains and losses associated with various data and practices typically applied in QPE. To this end, we conduct six experiments using 4 years of data from six laser optical disdrometers, two micro rain radars (MRRs), regular rain gauges, weather radar reflectivity and other operationally available meteorological data from existing stations. Each experiment addresses a typical question related to QPE. First, we measure the information about ground rainfall contained in various operationally available predictors. Here weather radar proves to be the single most important source of information, which can be further improved when distinguishing radar reflectivity–ground rainfall relationships (Z–R relations) by season and prevailing synoptic circulation pattern. Second, we investigate the effect of data sample size on QPE uncertainty using different data-based predictive models. This shows that the combination of reflectivity and month of the year as a two-predictor model is the best trade-off between robustness of the model and information gain. Third, we investigate the information content in spatial position by learning and applying site-specific Z–R relations. The related information gains are only moderate; specifically, they are lower than when distinguishing Z–R relations according to time of the year or synoptic circulation pattern. Fourth, we measure the information loss when fitting and using a deterministic Z–R relation, as is standard practice in operational radar-based QPE applying, e.g., the standard Marshall–Palmer relation, instead of using the empirical relation derived directly from the data. It shows that while the deterministic function captures the overall shape of the empirical relation quite well, it introduces an additional 60 % uncertainty when estimating rain rate. Fifth, we investigate how much information is gained along the radar observation path, starting with reflectivity measured by radar at height, continuing with the reflectivity measured by a MRR along a vertical profile in the atmosphere and ending with the reflectivity observed by a disdrometer directly at the ground. The results reveal that considerable additional information is gained by using observations from lower elevations due to the avoidance of information losses caused by ongoing microphysical precipitation processes from cloud height to ground. This emphasizes both the importance of vertical corrections for accurate QPE and of the required MRR observations. In the sixth experiment we evaluate the information content of radar data only, rain gauge data only and a combination of both as a function of the distance between the target and predictor rain gauge. The results show that station-only QPE outperforms radar-only QPE up to a distance of 7 to 8 km from the nearest station and that radar–gauge QPE performs best, even compared with radar-based models applying season or circulation pattern.
- Article
(5889 KB) - Full-text XML
- BibTeX
- EndNote
1.1 Approaches to quantitative precipitation estimation (QPE)
Quantitative precipitation estimation at high temporal and spatial resolution and in high quality are important prerequisites for many hydrometeorological design and management purposes. Besides rain gauges that have their own limitations (Huff, 1970; Nešpor and Sevruk, 1999; Nystuen, 1999; Yang et al., 1999), weather radar plays an increasingly important role in QPE: among other data sources, radar data have been used for urban hydrology (Thorndahl et al., 2017; Cecinati et al., 2017a; Wang et al., 2015), hydrological analysis and modeling (Bronstert et al., 2017; Rossa et al., 2005), real-time QPE (Germann et al., 2006), rainfall climatology (Overeem et al., 2009), rainfall pattern analysis (Kronenberg et al., 2012; Ruiz-Villanueva et al., 2012) and rainfall frequency analysis (Goudenhoofdt et al., 2017). For a comprehensive overview of radar theory and applications, see Battan (1959a, b), Sauvageot (1992), Doviak and Zrnic (1993), Rinehart (1991), Fabry (2015) or Rauber and Nesbitt (2018).
While the advantage of weather radar is that it provides 3-D observations at a high spatial and temporal resolution and with large coverage, unfortunately its use relies on some assumptions, which are sometimes justified and sometimes not. It is further hampered by considerable error and uncertainty arising from measuring the radar reflectivity factor Z (hereinafter referred to as reflectivity) instead of rain rate R, measuring at height instead of at the ground, and many other factors such as ground clutter, beam blockage, attenuation, second-trip echoes, anomalous beam propagation and bright-band effects. For a good overview on sources of errors, see Zawadzki (1984) or Villarini and Krajewski (2010).
In this paper we will focus on the first two aspects, namely the Z–R relation and the vertical profile of reflectivity. Typically, the Z–R relation is expressed by a deterministic exponential function of the form fitted to simultaneous observations of Z at height and R at the ground, the most common being the Marshall–Palmer relation (Marshall and Palmer, 1948). Much work has since been carried out to acknowledge the strongly nonlinear and time-variant nature of this relation (Lee and Zawadzki, 2005; Cao et al., 2010; Adirosi et al., 2016), the variability of reflectivity from high altitude to the ground (Joss et al., 1990) and correcting for the vertical profile of reflectivity (Vignal et al., 1999, 2000). The transition of the Z–R relations from at height to the ground was investigated by Peters et al. (2005). Much effort has also been spent on ways to improve QPE by combining radar with other sources of information such as rain gauges (Goudenhoofdt and Delobbe, 2009; Wang et al., 2015) or numerical weather prediction (Bauer et al., 2015) and to quantify the uncertainty of radar-based QPE (Cecinati et al., 2017b).
In this context, it is the aim of this paper to suggest and apply a framework which would use relationships between data expressed as empirical discrete probability distributions (dpd's), and would measure the strength of relations and remaining uncertainties with measures from information theory. Comparable approaches have been suggested by Sharma and Mehrotra (2014) and Thiesen et al. (2019): the former use an information-theoretic approach to formulate prediction models for cases where physical relationships are only weakly known but observational records are abundant; the latter emulate expert-based classification of rainfall–runoff events in hydrological time series by constructing dpd's from large sets of training data.
In particular, we investigate the effect of applying a purely data-based, probabilistic Z–R relation instead of a deterministic function fitted to the data. A similar probabilistic QPE approach was conducted, for example, by Kirstetter et al. (2015), by computing probability distributions of precipitation rates modeled from the conditional distribution of the precipitation rate for a given precipitation type and radar reflectivity factors on the basis of a 1-year data sample in the United States. However, in contrast to their approach using a simple theoretical model we utilize an information-theoretic framework. Similar work was also done by Yang et al. (2017), who developed a new relationship converting the vertical profile of reflectivity (VPR) to rain rates using a terrain-based weighted random forest method. The potential advantage of applying a probabilistic relation is that it yields joint statements of both the value of R and the related estimation uncertainty. That is to say, with our approach we do not want to provide a deterministic, single-valued rain rate, but promote the use of probabilistic QPE, which adequately reflects the (considerable) intrinsic uncertainties related to radar-based QPE. The history of radar meteorology shows that the most important part is quality control and error handling. With our approach we want to provide a probable rain rate value range and distribution, which for users has the added value of knowing intrinsic uncertainties (included in the systematic and random parts of the error; Kirstetter et al., 2015) compared with a single-valued QPE value. This is similar to ensemble approaches in operational weather forecasting. By knowing a predictive distribution, rather than a single value, the user will make better-informed decisions, especially in the case of extreme events such as flash flood forecasting. And if the user requires a single-valued statement, a distribution can always be collapsed to a single value, e.g., by calculating the mean or mode, whereas this is not possible in the opposite direction. We further test the potential of various operationally available observables such as synoptic circulation patterns (CP), convective and other meteorological indices (retrieved from rawinsonde data), meteorological ground variables and season indicators to distinguish typical Z–R relationships. The idea is to improve QPE by applying Z–R relationships tailored to the prevailing hydrometeorological situation as expressed by the predictors. Lastly, we use a comprehensive data set from 4 years of 1 h data available from one C-band weather radar, two vertical micro rain radars (MRR), six laser beam disdrometers and six rain gauges set up in the 288 km2 catchment of the Attert, Luxembourg, (Fig. 2) to evaluate the information gains with respect to ground rainfall when moving from measuring at height to measuring closer to the ground.
The remainder of the paper is structured as follows: in the next section, we briefly present the experiments carried out in the paper; in Sect. 2, we give a short overview on concepts and measures from information theory (Sect. 2.1) and on the methods (Sect. 2.2) and data (Sect. 2.3) used in the study; in Sect. 3, we present and discuss the results of all experiments; and our conclusions are presented in Sect. 4.
1.2 Design of experiments
We conduct a total of six experiments. In Experiment 1, we investigate the information on ground rainfall contained in various predictors, such as weather radar observations alone or in combination with additional, operationally available hydrometeorological predictors. In Experiment 2, we investigate the effect of limited data on the uncertainty of ground rainfall estimation for various data-based models. In Experiment 3, we examine the degree to which the empirical Z–R relationship in the 288 km2 test domain varies in space, and the minimum data sets that are required to support the use of site-specific Z–R relations. In Experiment 4, we evaluate the effect of functional compression by measuring the information loss when using the deterministic Marshall–Palmer relationship instead of the empirical, “scattered” relationship between Z and R as contained in the data. In Experiment 5, we investigate information gains along the radar path, i.e., when we use observations of the reflectivity measured increasingly close to the ground. We start with observations from weather radar at height, continue with observations from MRR along a vertical profile and finally use disdrometer observations of the reflectivity at the ground. In the last experiment, Experiment 6, we compare two methods of QPE, radar-based and rain-gauge-based, using information measures and explore the benefits of merging them.
2.1 Concepts and measures from information theory
Since its beginnings in communication theory and the seminal paper of Claude Shannon (Shannon, 1948), information theory (IT) has developed into a scientific discipline of its own, with applications ranging from meteorology (Brunsell, 2010) and hydrology (Pechlivanidis et al., 2016; Gong et al., 2014; Loritz et al., 2018) to geology (Wellmann and Regenauer-Lieb, 2012) any many others. Information theory has been proposed as one important approach to advance catchment hydrology to deal with predictions under change (Ehret et al., 2014). A good overview on applications in environmental and water engineering is given in Singh (2013), and Cover and Thomas (1991) provide a very accessible yet comprehensive introduction to the topic.
Please note that while the concepts of IT are universal and apply to both continuous and discrete data and distributions, we will, for the sake of clarity and brevity, restrict ourselves to the latter case and work with discrete (binned) probability distributions throughout all experiments.
2.1.1 Information
The most fundamental quantity of IT, information I(x), is defined as the negative logarithm of the probability p of an event or signal x (see Eq. 1). In this context the terms “event” and “signal” can be used interchangeably to refer to the outcome of a random experiment, i.e., a random draw from a known distribution.
Depending on the base of the logarithm, information is measured in (nat) for base e, (hartley) for base 10 or (bit) for base 2. We will stick to the unit bits here as it is the most commonly used (especially in the computer sciences) and because it offers some intuitive interpretations. Information in the context of IT has a fundamentally different meaning than in colloquial use, where it is often used synonymously with “data”.
Information can be described as the property of a signal that effects a change in our state of belief about some hypothesis (Nearing et al., 2016, Sect. 2.2). This definition has important implications: firstly, in order to quantify the information content of a signal, we have to know (or at least have an estimate) its occurrence probability a priori. Secondly, missing information can be seen as the distance between our current state of belief about something and knowledge, which establishes a link between the concepts of uncertainty and information. Information is carried by data, and, interestingly, the information content of the same data reaching us can be different depending on our prior state of belief: if we already have knowledge prior to receiving these data, its information content can only be zero and in all other cases it can only be as large as our prior state of belief. Therefore, information can be interpreted as a measure of surprise: the less probable an event is, the more surprised we are when it occurs, and the more informative the data are in revealing this to us. The dependency of information content on our prior state of belief is expressed by the prior probability p that we assign to the particular event.
Compared to working with probabilities, using its log-transforms – information – has the welcome effect that counting the total information provided by a sequence of events is additive, which is computationally more convenient than the multiplicative treatment of probabilities.
2.1.2 Information entropy
Information entropy H(X), or simply entropy is defined as the expected or average value of information (see Eq. 2) of a specific value or bin of a data set X=x1, x2, …, xn. This means that if information is the additional insight gained from the disclosure of the outcome of a single random experiment, then entropy is the average additional insight if the experiment is repeated many times. Thus, it is independent, identically distributed (iid) sampling of the entire underlying probability density function (pdf). Again, we can use the terms “expected information” and “expected uncertainty” as flip-side expressions of the same thing (more details on the interpretation of entropy as uncertainty are presented by Weijs, 2011, chap. 3).
In Eq. (2), I(x) indicates information and E is the expected value.
While information is a function of the occurrence probability of a particular outcome only, entropy is influenced by and is a measure of the shape of the entire pdf. Therefore, a pdf with only a single possible state of probability p=1 has an entropy of zero: there will be no surprise from the disclosure of any random draw, as we already know the result in advance. If, in contrast, the probability mass is spread evenly over the entire value range, entropy will be maximized. Therefore, uniform distributions serve as maximum entropy (minimum artificially added information) estimates of unknown pdfs.
Like the variance of a distribution, entropy is a measure of spread, but there are some important differences: while variance takes the values of the data into account and is expressed in (squared) units of the underlying data, entropy takes the probabilities of the data into account and is measured in bit. Variance is influenced by the relative position of the data on the measure scale and dominated by values far from the mean; entropy is influenced by the distribution of probability mass and is dominated by large probabilities. Some welcome properties of entropy are that it is applicable to data that cannot be placed on a measure scale (categorical data), and that it allows comparison of distributions from different data due to its generalized expression in bit.
2.1.3 Conditional entropy
So far, we know that entropy is as a measure of the expected information of a single distribution. We could also refer to this as a measure of self-information, or information we have about individual data items when the data distribution is known. If we do not only have a data set X=x1, x2, …, xn of single data items available, but joint data sets of paired data items X, Y=x1 y1, x2 y2, …, xn yn, then an obvious question to ask is “What is the benefit of a priori knowledge of a realization y coming from Y when we want to guess a particular realization x coming from X?”. In practice, this situation appears each time we want to make predictions about a quantity of interest x by exploiting available, related data, with the prerequisite that we know the general relation between the two data sets. Expanding the definition of entropy, conditional entropy H(X|Y) is defined as the probability-weighted (expected) entropy of all distributions of X conditional on the prior knowledge of Y=y (see Eq. 3).
For example, suppose we want to predict ground rainfall (our target X) based on radar reflectivity measurements (our predictor Y). The general relation between the two can be derived from a time series of joint observations and can be expressed by their joint distribution. This empirical relation is assumed to be both invariant, i.e., valid also for predictive situations, and representative, i.e., a good approximation of the “true” relation constructed from a hypothetical, infinitely long data set. Now, if in a particular predictive situation (i.e., at a particular point in time) we know the particular reflectivity value, then our best prediction of the corresponding rainfall value is the distribution of all past rainfall observations measured in combination with this particular reflectivity value.
If X and Y are completely independent, then prior knowledge of y when guessing x from a data pair (x.y) does not help at all. In this case each conditional distribution equals the marginal distribution p(X|Y), and the conditional entropy H(X|Y) is exactly equal to the unconditional entropy H(X). While such a situation is clearly not desirable, it also provides us with the useful insight that even if we apply a completely useless predictor, we can never make worse guesses than if we ignored it altogether. This is called the “information inequality” (Eq. 4), or simply “information can't hurt”. For the complete proof, see Cover and Thomas (1991) (p. 28).
2.1.4 Cross entropy
Entropy and conditional entropy measure information contained in the shape of distributions and the underlying data. Their calculation depends on prior knowledge of a pdf of these data and implies the assumption that this pdf is invariant and representative. In practice, this condition is not always fulfilled, either because we construct the pdf from limited data or because the system generating the data is not invariant. In these cases we work with approximations, or models, of the pdf, which means we estimate the information attached to a signal based on imperfect premises, which we in turn pay for with increased uncertainty. Cross entropy as defined in Eq. (5) quantifies exactly this.
In Eq. (5), p is the true probability distribution of the data, and q is the distribution that is assumed to be true. This means we calculate the information content of a particular signal based on its a priori known but only approximately true occurrence probability q(x). However, as we draw from the real distribution p, this particular signal really occurs with probability p(x). The larger the mismatch between p and q, the more additional questions we have to ask. In the best case, if premises are correct and q is identical to p, Hpq will be equal to H. In the worst case Hpq will go to infinity. An accessible and comprehensive treatment of this topic can be found in Weijs (2011), chap. 3.5.
2.1.5 Kullback–Leibler divergence
If both the entropy of a distribution and the cross entropy between the true distribution and an approximation (a model) thereof are known, we can separate these two components of total uncertainty: uncertainty due to the shape of the true distribution, and uncertainty because we do not know it exactly. The latter is measured by the Kullback–Leibler divergence (see Eq. 6 and Kullback and Leibler, 1951). It can either be calculated by the probability-weighted difference of the true and assumed-to-be-true occurrence probabilities, or by subtracting the entropy from the cross entropy.
2.2 Modeling and evaluation strategy
2.2.1 Data-based models and predictions, information-based model evaluation
Suppose we have a data set of many repeated, joint observations of several variates (data tuples), e.g., a time series of joint observations of R and Z. For each data tuple we can consider their values as coordinates in a multidimensional space, for which the number of dimensions equals the number of variates. Let us further suppose we choose, separately for each variate, a value range and a strategy to subdivide it into a finite set of bins. The first can be based on the observed range of data or on physical considerations, the latter on the resolution of the raw data or on user requirements about the resolution at which the data should be evaluated or at which predictions should be made. In this context, many methods for choosing an optimal binning strategy have been suggested (e.g., Knuth, 2013), but the most popular and straightforward method that concurrently introduces minimal side information is still uniform binning, i.e., splitting of the value range into a finite number of equal-width bins. Throughout this paper, we will stick to uniform binning.
With range and binning chosen, we can map the data set into a multivariate, discrete frequency distribution as shown in Fig. 1a. Normalization with the total number of data tuples yields the corresponding multivariate, discrete probability distribution (dpd). Note that the mapping comes at the price of a certain information loss: firstly, we lose the information about the absolute and relative position of the data tuples in the data set (e.g., for time series data, we discard the time stamp and the time order of the data), secondly we lose any information about the data tuple values at resolutions higher than the bin width. Nevertheless, the way that the probability mass is spread within the coordinate space is an indication of its structuredness, and its entropy is a direct measure thereof. High values of entropy indicate that the probability mass is widespread, which also means that we are highly uncertain when guessing a particular data tuple randomly drawn from the dpd. Conversely, if all probability mass is concentrated in a single bin, entropy will be zero and we can predict the values of a data tuple randomly drawn from the dpd with zero uncertainty.
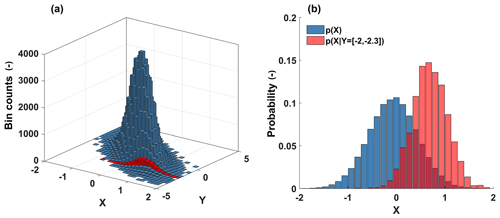
Figure 1Illustration of a bivariate conditional probability distribution as a simple data-based predictive model. (a) Joint histogram of target X and predictor Y (blue). Conditional histogram of target X given predictor values from the interval [−2, −2.3] (red). (b) Marginal (unconditional) probability distribution of target X (blue) and conditional probability distribution of target X given predictor values from the interval [−2, −2.3] (red).
So far we have used entropy to measure uncertainty as if we have had to guess all values of a data tuple randomly drawn from an a priori known distribution. However, often we do not only know the distribution a priori, but we also have knowledge of the values of parts of the data tuples (e.g., we know Z and the empirical Z–R relation and want to predict R). In this case, our uncertainty regarding the target variate R given the predictor variate Z and the relation among the two can be measured by conditional entropy, which we know from Eq. (4) is always smaller than or equal to the unconditional entropy of the target. In Fig. 1a, the conditional frequency distribution of the target X given predictor Y is shown in red; in Fig. 1b, the related conditional probability distribution,also in red, and the unconditional probability distribution of the target, in blue, are shown.
In short, we can consider a dpd constructed from a data set as a “minimalistic predictive model”, which, given some values for the predictor variates, provides a probabilistic prediction of the target variate. It is minimalistic in the sense that it involves only a small number of assumptions (representativeness of the dpd) and user decisions (choice of the binning scheme). Compared with more common modeling approaches, where relations among data are expressed by deterministic equations, the advantage of a dpd-based model is that it yields probabilistic predictions in the form of conditional dpd's, which include a statement about the target value and the uncertainty associated with that statement. Also, as dpd-based modeling does not involve strong regularizations, it reduces the risk of introducing incorrect information. When building a standard model, choosing a particular deterministic equation to represent a data relation, which is a common form of regularization, involves the risk of introducing bias, and it ignores predictive uncertainty. In this context, Todini (2007) provides a very comprehensive discussion on the relative merits and problems of data-based models and models relying on additional information in the form of physical knowledge, as well as the role and treatment of predictive uncertainty.
Things are different, however, if we apply the model to a new situation, i.e., if we construct the model from one data set and use it with predictor data of another under the assumption that the predictor–target relation expressed by the model also holds for the new situation. This is clearly only the case if the learning and the application situation are identical; however, in most cases the situations will differ and we will pay for this inconsistency with additional uncertainty. We can measure this uncertainty using the Kullback–Leibler divergence (Eq. 6) between the dpd we use as a model and the true dpd of the application situation. Total predictive uncertainty is then expressed by cross entropy (Eq. 5) and can be calculated as the sum of the predictive uncertainty given a perfect model (expressed by conditional entropy), which is limited by the amount of information the predictors contain about the target and by the inadequacy of the model (expressed by Kullback–Leibler divergence).
We will apply this approach to construct and analyze predictive models throughout the paper, and use it to learn about the information content of various predictors about our target, ground rainfall R, and learn about the information losses when applying predictive models that were, e.g., constructed from limited data sets, constructed at different places, or simplified by functional compression. Note that expressing relations among predictor and target data by dpd's is not limited to data-based models, in fact functional relationships of any kind (e.g., the Marshall–Palmer Z–R relation) can be expressed in a dpd. In that sense, the framework for model building and testing as well as the measures to quantify uncertainty that we use here are universally applicable.
2.2.2 Benchmark models and minimum model requirements
Expressing predictions by probability distributions, and expressing uncertainty as “information missing” as described in the previous sections has the advantage that we can build default models providing lower and upper bounds of uncertainty, which we can then use as benchmarks to compare other models against. The smallest possible uncertainty occurs if the predictive distribution of the target is a Dirac, i.e., the entire probability mass is concentrated in a single bin. In such a case, irrespective of the number of bins covering the value range, the entropy of the distribution is zero: HDirac=0. If such a case occurs, we know that we have applied fully informative predictors and a fully consistent model. Things are more interesting when we want to formulate upper bounds: the worst case occurs if we use a model which is unable to provide a prediction for a set of predictors in the application case. This happens when the particular situation was never encountered in the learning data set, but appears during application. In this case, p(x) in Eq. (6) will be nonzero, q(x) will be zero and Kullback–Leibler divergence will be infinite, indicating that the model is completely inadequate for the application situation. In this case total uncertainty will also be infinite, no matter how informative the predictors are. However, infinity as an upper bound for uncertainty is not very helpful, and we can do better than that: if the above case occurs, we can argue that the model is inadequate just because it learned from a limited data set, and as we require the model to provide a prediction for all predictive situations, we can allocate a small but nonzero probability to all bins of the model. In this paper, we did so using the minimally invasive maximum entropy approach suggested by Darscheid et al. (2018). Note that this was only required in experiments 2–4, when we calculated Kullback–Leibler divergence between a reference and models based either on very small samples (experiments 2 and 3) or deterministic relations (Experiment 4).
Given that we successfully avoid infinite Kullback–Leibler divergence, the worst thing that can happen is that our predictions are completely uninformative, i.e., we provide a uniform distribution across the entire value range of the target. In this case, the entropy of the distribution is equal to the logarithm of the number of bins: Huniform=log 2 (number of bins). This means that for all cases where we are sure that infinite Kullback–Leibler divergences will not occur, we can provide an upper limit of total uncertainty which is dependent on the required resolution of our predictions.
Finally, for the special cases where we know that the model we use is perfect (typically because we apply it to the same situation it was constructed from), we know that Kullback–Leibler divergence is zero, and total uncertainty equals conditional entropy. In this case, we can state another upper bound for uncertainty: if at worst the predictors we use are completely uninformative, conditional entropy will be equal to the unconditional entropy of the target distribution (see Eq. 4).
We will use these lower and upper bounds for total uncertainty throughout the experiments to put the performance of the tested models into perspective.
2.2.3 Sampling strategy
In experiments 2 and 3 we investigate the effect of limited sample size, i.e., the information loss (or uncertainty increase) if we do not construct a model from a full data set, but from subsets drawn thereof. This corresponds to the real-world situation of building models from available, limited data. For the sake of demonstration, we assume in the experiments that a long and representative reference data set is available for evaluation. While this is clearly not the case in real-world situations, we can get answers from such experiments for practically relevant questions such as “what is a representative sample, i.e., how many observations are required until a model built from the data does not change further with the addition of observations?” or “should we build a model from locally available but limited data, or should we use a model learned elsewhere, but from a large data set?”.
Throughout the experiments, we apply simple random sampling without replacement to take samples from data sets. In order to reduce effects of chance, we repeat each sampling 500 times, calculate the results for each sample and then take the average.
2.3 Data
This study uses data from various sources collected during a 4-year period (1 October 2012–30 September 2016) within the CAOS (Catchments As Organised Systems) research project. For more detail on project goals and partners see Zehe et al. (2014). QPE was an important component of CAOS, and to this end special focus was on measuring rain rates and drop size distributions (DSD) using six laser optical disdrometers, two vertical pointing K-band micro rain radars, standard rain gauges and weather radar. Table 1 provides an overview of these and additionally used data.
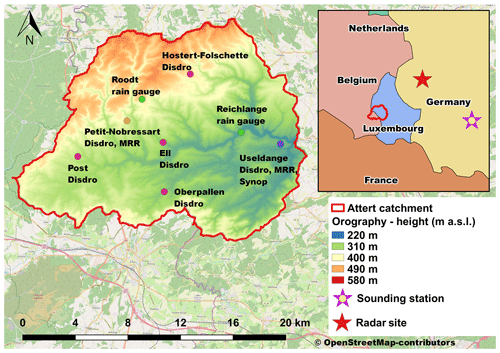
Figure 2The position of the Attert catchment in Luxembourg and Belgium with superimposed orography (in m a.s.l.) and the locations of the MRR's, disdrometers, rain gauges, the synoptic station (ASTA) and radar site (Neuheilenbach), and the rawinsonde launching (sounding) station (Idar-Oberstein – WMO-ID 10618) as well as the scale and orientation of the small-scale map. © OpenStreetMap contributors 2019. Distributed under a Creative Commons BY-SA License.
Table 1Summary of the raw data used in the experiments: description, summary statistics and binning.
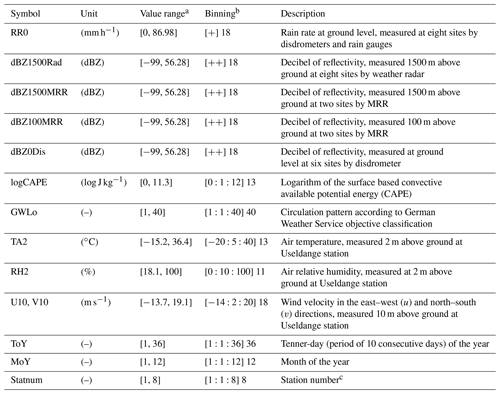
a [min, max]; b [center of first bin, uniform bin width, center of last bin] number of bins; c 1: Ell, 2: Hostert–Folschette, 3: Oberpallen, 4: Petit-Nobressart, 5: Post, 6: Useldange, 7: Reichlange, 8: Roodt; + irregular binning with edges [−0.1 0.19 1 2 4 6 8 10 15 20 25 30 40 50 60 70 90 110 130]; irregular binning with edges [−100 11.5 23 27.8 32.6 35.5 37.5 39 41.8 43.8 45.4 46.6 48.6 50.2 51.5 52.5 54.3 55.7 56.8].
2.3.1 Study area and hydroclimate
The project was conducted in the Attert Basin, which is located in the central western part of the Grand Duchy of Luxembourg and partially in eastern Belgium (see Fig. 2) with a total catchment area of 288 km2. The landscape is orographically slightly structured, with a small area underlain by sandstones in the south, with heights up to 380 m a.s.l, a wide area of sandy marls in the center part, in which the main Attert River flows from west to east, and an elevated region in the north which is part of the Ardennes Massif and reaches elevations up to 539 m a.s.l.
The study area is situated in the temperate oceanic climate zone (Cfb according to the Köppen–Geiger classification; Köppen and Geiger, 1930). Precipitation is mainly associated with synoptic flow regimes with a westerly wind component and amounts to around 850 mm (Pfister et al., 2005, 2000), ranging from 760 mm in the center to about 980 mm in the northwestern region (Faber, 1971) due to orography and luv-lee effects. Especially during intensive rain events within a synoptic northwesterly flow regime, the main part of the Attert region lies in the rain shadow of the Ardennes, whereas the outermost northwestern part is excluded from this lee effect and is still within the region of local rain enhancement by upward orographic lift (Schmithüsen, 1940). This also partly explains local differences in the annual precipitation regime: while in the elevated regions of the northwest, the main rain season is (early) winter, in the central lowlands convective summer rainfall also provides a substantial contribution. Interestingly, the latter mainly occurs along two main storm tracks: one northeastern starting in the southwest corner of Luxembourg and touching the study area in the east; one northeastern starting in Belgium and touching the study area in the west.
In our study, we investigated both the effects of location and season on drop-size distributions and ultimately on QPE.
2.3.2 Radar data
We used 10 min reflectivity data from a single polarization C-band Doppler radar located in Neuheilenbach (see Fig. 2), and operated by the German Weather Service (DWD). The raw volume data set has an azimuthal resolution of 1∘ and a 500 m radial resolution. The antenna's −3 dB-beamwidth is 1∘. The distance of the study area from the radar site is between 40 and 70 km, which renders high-resolution data and avoids cone of silence issues. The raw data were filtered by static and Doppler clutter filters and bright-band correction (Hannesen, 1998), but no attenuation corrections were applied. Second trip echoes (Bückle, 2009) as well as obvious anomalous propagation (anaprop) echoes were also removed, especially as the latter are prominent in this area during fall and spring (Neuper, 2009). From the corrected data we constructed a pseudo PPI (plan position indicator) data set at 1500 m above ground and, to make the data comparable to and combinable with all of the other data used, we took hourly averages.
2.3.3 MRR data
We also used drop size spectra measured at 1500 and 100 m above ground by two vertical pointing K-band METEK micro rain radars (MRR) (Löffler-Mang et al., 1999; Peters et al., 2002) located at the Useldange and Petit-Nobressart sites (Fig. 2). We operated the MRRs at 100 vertical meters and a 10 s temporal resolution, but for reasons of storage and processing efficiency did all further processing on 1 min aggregations thereof. The raw Doppler spectra were transformed to drop size distributions via the drop size–fall velocity relation given in Atlas et al. (1973). From the drop size distributions the rain rate and the reflectivity were calculated using the 3.67th and the 6th statistical moments of the drop size distributions (as in Doviak and Zrnic, 1993; Ulbrich and Atlas, 1998; Zhang et al., 2001). In doing so, we assumed the vertical velocity of the air to be negligible, although this may sometimes play a significant role (Dotzek and Beheng, 2001). Furthermore, the intensity of the electromagnetic waves of the MRR is attenuated on the propagation path by different processes. Due to the short wavelength, the attenuation by water vapor is relatively strong. This process is neglected in this study. Attenuation due to rain can also be significant, especially at moderate and higher rain rates, if higher altitudes (with a long beam propagation path) are considered. Without considering the attenuation by rain, a height dependent underestimation of the rain rates would be retrieved. Therefore, we corrected for attenuation assuming liquid rain by applying a stepwise path-integrated rain attenuation following the manufacturer indications. As previously undertaken, we converted the data to 1 h values by averaging (reflectivity) and summation (rain sum).
2.3.4 Disdrometer data
We also deployed six second-generation OTT particle size and velocity (Parsivel2, Löffler-Mang and Joss, 2000) optical disdrometers in the study area to measure drop size distributions at ground level (Fig. 2) at a 1 min resolution. Two were located at the same sites as the MRRs (Useldange and Petit-Nobressart); the others were placed such as to both capture the hydroclimatic variations in the study area and to cover it as uniformly as possible. We applied a quality control to the raw data as described by Friedrich et al. (2013a, b), converted the filtered data to drop size concentrations per unit air volume to make them comparable to the weather radar and MRR data, converted them to reflectivity and rain rate using the 3.67th and 6th statistical moments of the drop size distributions and finally took 1 h averages and sums thereof.
2.3.5 Rain gauge data
Next to the rain rate retrieved from the disdrometer data, we also used additional observations from standard tipping-bucket rain gauges at the Useldange, Roodt and Reichlange sites (Fig. 2). Quality-controlled rain gauge data from Useldange and Roodt were provided by the Administration des services techniques de l'agriculture (ASTA), which operates a nationwide network of surface weather stations for agricultural guidance. Raw rain gauge data at Reichlange were provided by the Hydrometry Service Luxembourg. We applied plausibility checks to all of these data, eliminated questionable data, cases with solid precipitation (based on the output of the hydrometeor classification algorithm of the disdrometers) and finally took 1 h sums.
2.3.6 Additional predictors
In addition to direct observations of precipitation and drop size spectra, we collected a number of operationally available data to test their value as additional predictors for QPE. We selected standard meteorological in situ observations such as 2 m temperature, relative humidity, zonal and meridional wind speeds, season indicators such as month and tenner-day of the year as well as synoptic indices such as convective available potential energy (CAPE) and classified circulation pattern. The latter two are operationally provided by the German Weather Service. All predictors are listed in Table 1.
The in situ observations were taken from ASTA station Useldange (Fig. 2), and like all other observations underwent additional quality filtering and 1 h aggregation. The CAPE values are based on rawinsonde data obtained from Idar-Oberstein station (WMO-ID: 10618) located about 90 km east of the study area with a temporal resolution of 6h. The soundings were downloaded from the University of Wyoming home page (see data availability) and checked for contamination by convection as described in Bunkers et al. (2006). The CAPE values were calculated as surface-based CAPE using the virtual temperature (Vasquez, 2017). Selecting CAPE as a descriptor for raindrop size distribution followed the reasoning that updraft strength has an influence on the size of the raindrops (Seifert and Beheng, 2006). We used a base-10 logarithmic transform of CAPE to assure high resolution at lower CAPE values in addition to the sufficient population of the higher classes.
With respect to classified circulation patterns, the German Weather Service provides a daily objective classification of the prevailing circulation pattern over Europe into one of 40 classes (Dittmann et al., 1995). It is based on numerical weather analysis from one of the operational forecast models of the German Weather Service at 12:00 UTC and considers wind direction, cyclonality (high- or low-pressure influence) and atmospheric humidity. Selecting the circulation as a predictor was based on the perception that it should contain information about both the prevailing precipitation process (stratiform or convective) and the presence and origin of air masses, which could influence drop size spectra due to the presence or absence of characteristic cloud condensation nuclei and ice nucleation nuclei.
2.3.7 Binning choices
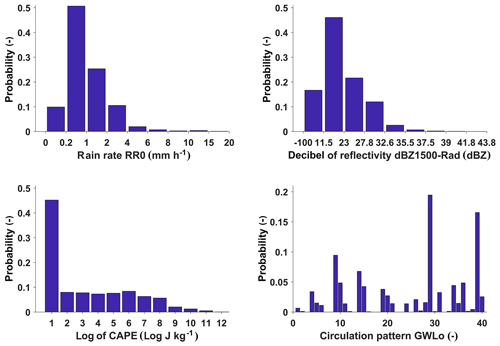
Using all of these data in the methods as described in Sect. 2.2 requires binning. Our general binning strategy was to cover the entire data range, divide it into as few bins as possible to keep bin populations high, but at the same time use enough bins to resolve the shape of the data distributions. We used uniform binning whenever possible, but for strongly skewed data such as reflectivity and rain rate we applied irregular binning. For the latter, we defined the edges of the first bin so as to cover the range from the smallest possible value (0 mm) and 0.2 mm, which is the detection limit of most tipping-bucket rain collectors. Therefore, this bin essentially covers all cases of nonzero but irrelevant rain. For the last bin, we set the upper edge so that it still covered rainfall based on the largest observed reflectivity value transformed to rain rate by the standard Marshall–Palmer Z–R relation (Z=200R1.6), which was 119.9 mm h−1. For the bins in between, we increased the bin width with rain rate (see footnote to Table 1) to acknowledge both the increasing uncertainty and sparsity of high-rainfall observations. With the binning for rain rate fixed, we applied the Marshall–Palmer relation in reverse to get the corresponding bin edges for reflectivity.
2.3.8 Data filter
Rainfall is an intermittent process, and quite expectedly most of our 4-year series contained zeroes for rainfall. If we had used this complete data set for analysis, the results would have been dominated by these dry cases; however, these cases were not what we were interested in. Therefore, we applied a data filter to select only the hydro-meteorologically relevant cases with measurements from all available stations and at least two rain gauges showing rainfall ≥ 0.5 mm h−1. Additionally, cases with solid precipitation were excluded using the output from the disdrometers' present weather sensor software. In total, 11 984 data sets passed this “minimum precipitation” filter, which amounts to almost 17 months of hourly data.
In Fig. 3, for the filtered data binned probability distributions of the most important variables are shown.
3.1 Experiment 1: information in various predictors
In this experiment we explore the information content regarding ground rainfall R in various predictors (see Table 1). We selected the predictors with the constraint that they are operationally available at any potential point of interest, which applies most importantly to reflectivity measured by weather radar, but also to the predictors we assumed to be spatially invariant within the test domain: convective available potential energy (as surface based CAPE), circulation pattern, air temperature and humidity, wind, and season. We excluded reflectivity measurements by MRR and disdrometer, as these are usually only available at a few locations.
We used ground rainfall observations from the eight rain gauges in the test domain as target data, filtered the raw data with the “minimum precipitation” filter and created models using various predictor combinations. We measured the usefulness of the predictors with entropy and conditional entropy (Eqs. 2 and 3). The results are shown in Table 2.
Table 2Entropy of the target (RR0) and the benchmark distribution (RR0 uniform), conditional entropies of the target given one or several predictors, non-normalized and normalized. Underlying data are from the filtered data set. Predictors are ordered by descending conditional entropy.
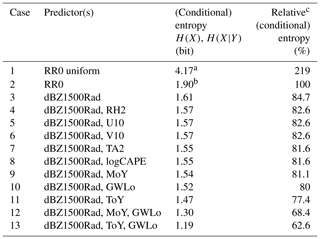
a Unconditional entropy of the benchmark uniform distribution; b Unconditional entropy of the target; c H(RR0|predictor(s))∕H(RR0) ⋅ 100.
There are two upper benchmarks we can use to compare the different QPE models against: unconditional entropy if we know nothing but the binning of the target and use a uniform (maximum entropy) distribution for prediction (case 1 in Table 2), and the unconditional entropy of the observed distribution of the target (case 2 in Table 2), which we used as a reference here. The difference between the two is considerable (119 %), which means that merely knowing the true distribution of RR0 is already a valuable source of information.
The next important source of information is radar reflectivities: if we use it as a single predictor (case 3), uncertainty is reduced by 0.28 bit or 15.3 % compared with RR0. Note that this approach directly applies the reflectivity data provided by the radar, no side information was added nor existing information in the data destroyed by applying an additional Z–R relation. This result shows, on the one hand, that radar reflectivity is one of the most important sources of information. On the other hand – as the reduction in uncertainty is quite low when RR0 is conditioned by dBZ1500Rad – the high variability in the Z–R relationship limits entropy reduction. The may be due in part to the effects of the vertical profile of reflectivity and attenuation at high rain rates.
Using each of the other predictors separately did not reduce uncertainty much (not shown); therefore, we only show results for the cases where they were applied as two-predictor models in combination with radar reflectivity (cases 4 to 11). If we compare the relative conditional entropies of their predictions to those of the radar-only model, we can see that neither the ground meteorological observations nor CAPE contained much additional information (cases 4 to 8). Instead, the three most informative models (cases 9 to 11) either distinguish the relation between R and Z by circulation pattern or by season, which corresponds to the operational practice of many weather services to use one Z–R relation for summer and one for winter.
Based on these results, we built and evaluated three-predictor models only with combinations of these relatively informative predictors (cases 12 and 13). The information gain from using three predictors in combination is considerable, and it reduced uncertainty to 68.4 % (case 12) and 62.6 % (case 13) compared with the “target-distribution-only case” (case 2). The benefit of applying a season-dependent and circulation-pattern-dependent relation between R and Z also becomes obvious if we compare case 3 (the radar-only model) with cases 12 and 13: in the first case, uncertainty is reduced by 16.3 %, in the latter by 22.1 %.
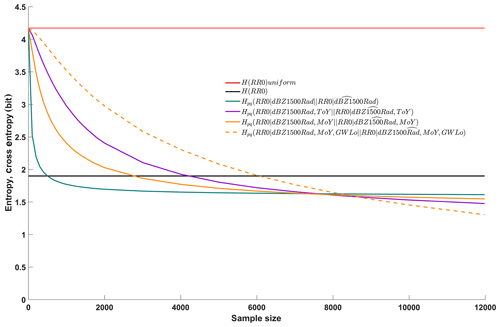
Figure 4Entropy of the unconditional target distribution (filtered data set, black line), entropy of the benchmark uniform distribution (filtered data set, red line), cross entropies between conditional distributions of the target given one, two and three predictors of the filtered data set and samples thereof (green, purple, yellow and dashed yellow lines, respectively). The “∧” symbol indicates a sample.
An obvious conclusion from these findings would be to build better models by simply adding more predictors, which according to the information inequality equation (Eq. 4) never hurts. In fact, when learning from limited data sets, adding enough predictors will, in the end, result in perfect models with zero predictive uncertainty. However, there is a catch to this, which is known as overfitting: in order for a model to be robust in the sense of “being only weakly sensitive to the presence or absence of particular observations in the learning data set” and “performing well not only within the training data set, but also on data unseen during training”, it must be supported by an adequate number of learning data, and this number grows exponentially with the number of predictors included in the model. So instead of adding more predictors, we will explore the robustness of our models in the next experiment.
3.2 Experiment 2: the effect of sample size
The data base and filter used here are identical to the previous experiment, so a set of 11 984 joint observations of the target (rain rate at the ground) and predictors (radar reflectivity, circulation pattern, tenner-day and month of the year) were available. From these data we built and tested a total of four predictive models, as described in Experiment 1: a one-predictor model applying radar reflectivity only, two two-predictor models applying radar reflectivity and tenner-day or month of the year, and a three-predictor model using radar reflectivity, month of the year and circulation pattern. The difference to Experiment 1 is that we now do not only apply the entire data set but also randomly drawn samples thereof to build the model (see Sect. 2.2 for an explanation of the sampling strategy). Each model is then applied to and evaluated against the full data set. In this case, total predictive uncertainty is measured by cross entropy (Eq. 5), which is the sum of conditional entropy of the target given the predictors for the full data set and Kullback–Leibler divergence of the sample-based model and the model built from the full data set (see Sect. 2.2).
The results are shown in Fig. 4 as a function of sample size. As in Experiment 1, we included the benchmark uncertainties for applying a maximum entropy model (red horizontal line, case 1 in Table 2) and a zero-predictor model (black horizontal line, case 2 in Table 2) to put the other models into perspective.
On the right margin of Fig. 4, cross entropies are shown for the case where the sample comprises the entire data set. In this case, Kullback–Leibler divergence is zero, and total uncertainty equals conditional entropy. This is the same situation as in Experiment 1, and the values correspond to those in Table 2 for cases 3, 9, 10 and 12. The three-predictor model (dashed yellow line) quite expectedly outperforms the two-predictor models (solid purple and yellow lines), which in turn outperform the one-predictor model (solid green line). However, things look different if only samples are used for learning. With respect to the one-predictor model, for very small sample sizes close to zero, the information content of the sample is close to zero; hence, the predictive uncertainty is close to that of the ignorant maximum entropy model (red line) and considerably higher than that of the zero-predictor model. However, when increasing the size of the sample just a little, its information content quickly rises and cross entropy drops. In fact, when learning the relation between radar reflectivity and ground rainfall from only about 2000 joint observations, the model is almost identical to a model learned from the full data set of 11 984 joint observations: Kullback–Leibler divergence is almost zero and cross entropy is almost as low as for the model built from the full data set. From this we can conclude that the full data set contains considerable redundancy, which in turn implies that we can build robust one-predictor models from the available data.
We can interpret the lines in Fig. 4 as learning curves, or more specifically they represent the information about the target contained in samples of different sizes. If we now consider the two two-predictor models and the three-predictor model and compare them to the one-predictor model, we can see that the more predictors we add, the slower the learning rates become and the longer learning takes (the curve inclinations are lower for small sample sizes, but remain nonzero for larger samples). For the two two-predictor models this means that samples larger than about 8000 (about two-thirds of the data set) are required before their total predictive uncertainties fall below that of the one-predictor model. For the three-predictor model, even samples larger than about 8500 are required, and the model interestingly continues to learn even for very large sample sizes (the yellow dashed line is still inclined, even for large samples).
The learning behavior of the models, which differs with the number of predictors used, is a manifestation of the “curse of dimensionality”, and visual examination of learning curves of different models as plotted in Fig. 4 allows two choices: for a given sample size, we can choose the best (least uncertain) model; for a given size data set, we can choose the model with the best trade-off between performance and robustness. For the latter choice, we can establish selection criteria such as “a model qualifies as robust if it learns from at maximum of two-thirds of the available data at least 95 % of what it can learn from the entire data set” and then choose the best model satisfying this criterion. From the models displayed here, according to our subjective choice, the two-predictor model using a month-specific relation between radar reflectivity and ground rainfall provides the best trade-off between performance and robustness.
3.3 Experiment 3: site-specific Z–R relations
In this experiment we investigate the information content in spatial position by learning and applying site-specific relations between radar reflectivity and ground rain rate (in the previous experiments we applied them in a spatially pooled manner). We used data filtered with the “minimum precipitation” filter again, so a set of 11 984 joint observations of ground rain rate and radar reflectivity were available. We included spatial information by simply using the ID number of each station (“Statnum” in Table 1) as an additional predictor, which means that we built and applied relations between reflectivity and rain rate at the ground specifically for each station in the test domain (see Fig. 2). As in the previous experiment, we evaluated the predictive performance of these models as a function of sample size with cross entropy. The results are shown in Fig. 5.
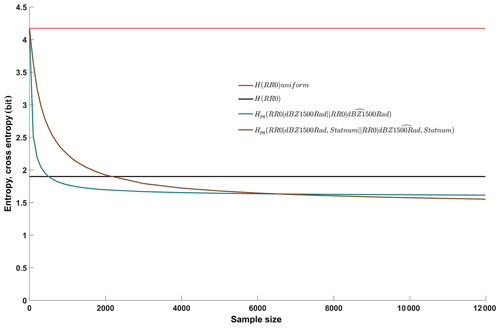
Figure 5Entropy of the unconditional, target distribution (filtered data set, black line, same as in Fig. 4), entropy of the benchmark uniform distribution (filtered data set, red line, same as in Fig. 4), cross entropies between conditional distributions of the target of the filtered data set and samples thereof: one-predictor model applying dBZ1500Rad (green line, same as in Fig. 4), two-predictor model applying dBZ1500Rad and station number (brown line). The “∧” symbol indicates a sample.
The red and black horizontal lines are the same as in Fig. 4 and (as previously) represent the benchmark unconditional entropies of the target for a maximum entropy uniform distribution and the observed distribution. A green line was also included in Fig. 4 and represents the conditional entropy of the one-predictor model applying radar reflectivity only. The brown line shows the performance of the two-predictor model including the station ID. The overall pattern is similar to Experiment 2: adding a predictor reduces the total uncertainty if the full data set is used for learning (at the right margin, the brown line lies below the green), but higher-predictor models require more data for learning (the green line descends more slowly and over a longer period than the brown). Here, the two-predictor model outperforms the zero-predictor model only for samples larger than 2200, and the one-predictor model only for samples larger than 6500.
Overall, the information gain of using site-specific Z–R relations is moderate (cross entropy of the radar-only model for the full data set is 1.61 bit, whereas it is 1.55 bit for the site-specific model) and lower than when distinguishing Z–R relations according to time or circulation pattern (cases 9, 10 and 11 in Table 2). This is not very surprising if we consider the extent of the test domain: the largest distance between two stations is 9.5 km (between Oberpallen and Useldange stations), and the largest elevation difference is 182 m (between Reichlange and Roodt stations). Across these relatively small distances, it appears reasonable that Z–R relations do not differ substantially. However, this could be different when working in larger domains or in domains with hydro-meteorologically distinctly different subdomains, such as lowlands and mountain areas or different climate zones (as shown, for example, in Diem, 1968).
3.4 Experiment 4: the effect of functional compression
In this experiment we evaluate the effect of functional compression by measuring the information loss when using a deterministic function to express the relation between radar reflectivity and ground rain rate instead of the empirical relation derived from the data. As before, we used all joint observations of radar reflectivity and ground rainfall passing the “minimum precipitation” filter. Each data pair is shown as a blue dot in Fig. 6, and we can see that a strong, positive and nonlinear relation exists between them. We already made use of this relation in Experiment 1 when we built a one-predictor model using reflectivity to estimate ground rainfall. Comparing cases 2 and 3 in Table 2 we can see that prior knowledge of reflectivity indeed contains valuable information, reducing total uncertainty by 15.3 % (100 % to 84.7 %).
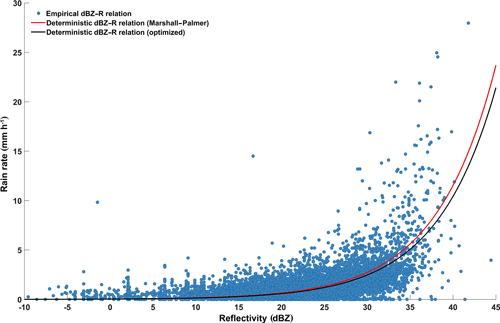
Figure 6Relation between target RR0 and predictor dBZ1500Rad. Empirical relation as given by the filtered data set (blue dots). Deterministic power-law relation according to Marshall and Palmer (1948) (red line); deterministic power-law relation with optimized parameters a=235 and b=1.6 (black line).
Let us suppose we would not have been in the comfortable situation of having joint observations of target and predictor to construct a data-based model, or suppose it would take too much storage or computational resources to either store or apply such a model. In these cases, it could be reasonable to approximate the “scattered” relation as contained in the data either using a deterministic function gained from other data or a deterministic function fitted to the data. In fact, this is standard practice. Expressing a data relation by a function drastically reduces storage space, is easy to apply and preserves the overall relation among the data. However, what we lose is information about the strength of that relation as expressed by the scatter of the data. Instead, when applying a deterministic function we claim that the predictive uncertainty of the target is zero.
Our aim here is to quantify the information loss associated with such deterministic functional compression. Applying a deterministic model is in principle no different than using a model learned from a subset of the data, as we did in Experiment 2: we use an imperfect model, which results in additional uncertainty which we can measure via Kullback–Leibler divergence between the true data relation and the model we apply (see Eq. 6). Total predictive uncertainty is then measured by cross entropy (Eq. 5) as the sum of conditional entropy (the uncertainty due to incomplete information of the predictor about the target) and Kullback–Leibler divergence (see Sect. 2.2).
For demonstration purposes we applied two typical deterministic Z–R relations of the form . The first is the widely used Marshall–Palmer relation (mostly attributed to Marshall and Palmer (1948) as, for example, in Battan (1959b) and Sauvageot (1992); however, the origin of this particular formula is unknown to the authors) with parameters a=200 and b=1.6. The Marshall–Palmer relation is often used as a default model if no better options or local data are available. For the second, we assumed the local reflectivity and rain rate observations to be available and used them to optimize parameter a by minimizing the root mean square error (RMSE) between the observed rain rate and the modeled rain rate using reflectivity observations. Following the recommendations by Hagen and Yuter (2003), we only varied a and kept b constant at 1.6. In the end, the optimized a=235 was not far from its Marshall–Palmer pendant and only reduced the RMSE slightly from 1.18 mm h−1 (Marshall–Palmer relation) to 1.17 mm h−1. Apparently, the default Marshall–Palmer relation already nicely fit our data. In Fig. 6, the two deterministic Z–R functions are plotted using red (Marshall–Palmer) and black (optimized Z–R relation) lines. Both capture the overall shape of the empirical Z–R relation quite well, except for high reflectivities where they tend to underestimate the observed rain rates. Applying such a deterministic Z–R relation to a given reflectivity observation is straightforward and yields a prediction of the related rain rate. However, from such a single-valued prediction we cannot infer the related predictive uncertainty, and the best we can do is to additionally provide the model's RMSE as a proxy.
As described above, we additionally used our information-based approach and calculated the conditional Kullback–Leibler divergence between the predictive distributions given by the empirical (perfect) and the deterministic (imperfect) models for all available data. From Eq. (6) we see that when comparing a reference distribution p to a model distribution q, a situation can occur where the latter is zero but the former is not, which means that an event is contained in the reference data that, according to the model, can never occur. In such a case the Kullback–Leibler divergence will be infinite, branding the model as completely inadequate. However, this verdict may seem too strict, e.g., if the model shows otherwise good agreement with reality, if we have reason to believe that the mismatch only occurred from a lack of opportunity due to a small data set rather than due to a principal mismatch of model and reference or, as in our case, if we know that we are using a deterministic approximation instead of the real data relation. In such cases, infinite divergence can be avoided by padding empty bins of the model distribution with small but nonzero probabilities, which we did by applying the minimally invasive maximum entropy approach suggested by Darscheid et al. (2018).
For our data, conditional Kullback–Leibler divergence for the Marshall–Palmer model was 3.43 bit, and it was 2.69 bit for the optimized model. Added to the conditional entropy of the empirical Z–R relation, this resulted in total predictive uncertainties of 5.04 and 4.30 bit, respectively. In terms of relative contributions, this means that 68 % (Marshall–Palmer) and 62.5 % (optimized model) of total uncertainty are due to deterministic functional compression. This is quite considerable, and even more so if we compare these results to the two benchmark cases in Table 2 (cases 1 and 2): even the default and safe-side model of applying a uniform distribution (case 1) involves smaller predictive uncertainty than the deterministic models. This seems counterintuitive at first when recalling the good visual agreement of the empirical and deterministic Z–R relations in Fig. 6. The reason for such large Kullback–Leibler divergences is the relatively high binning resolution for rain rate (Table 1) in combination with the way Kullback–Leibler divergence is computed: probability differences are calculated bin by bin and irrespective of probabilities in neighboring bins. This means that even a small over- or underestimation of a model, with an offset of the main probability mass by just one bin compared with observations can result in large divergence, which can, in the end, even exceed that of a prudent model spreading probability mass evenly over the data range. For the data used in this experiment, we assume that the agreement between deterministic model predictions and observations would quickly increase when coarse-graining the binning. This would be an interesting question to pursue in a future study, but for now we restrict ourselves to the main conclusion of this experiment: as long as learning about and application of data relations is carried out in the same data set, compression of probabilistic data relationships to deterministic functions will invariably increase uncertainty about the target. However, for the forward case, i.e., cases where there are no data available for learning but predictions are nevertheless required, application of robust deterministic relations capturing the essential relation between available predictors and the target is useful.
3.5 Experiment 5: information gains along the radar path
In this experiment we explore how the information content about ground rainfall in reflectivity observations is related to the measurement position along a vertical profile above the rain gauge, and how it is related to the measurement device. To this end, we used data from two sites, Petit-Nobressart and Useldange (see Fig. 2), where a range of reflectivity observations along a 1500 m vertical profile starting at ground level was available: disdrometer observations of reflectivity and rain rate at ground level, MRR reflectivity observations at a 100 m resolution between 100 and 1500 m above ground, and observations from C-band weather radar at 1500 m. With the goal in mind of providing guidance for the layout of future QPE sensor networks, we addressed the following questions: “are MRR observations at 1500 m more informative than weather radar observations taken at the same height?”; “how much information is gained if we use near-surface instead of elevated MRR observations, thus omitting the influence of the vertical profile of reflectivity?”; and finally “how much information is lost if we measure reflectivity instead of rainfall at ground level?”.
In contrast to the previous experiments, we were restricted to two (instead of eight) sites with MRR's installed. This made the application of the standard “minimum precipitation” filter (see Sect. 2.3) inappropriate. Thus, instead of filtering the raw data by at least two rain gauges showing rainfall ≥ 0.5 mm h−1, we now applied this threshold separately to each of the sites. At Petit-Nobressart a total of 1241 data tuples passed the filter, at Useldange 612 data tuples passed the filter (Useldange began operation a year after Petit-Nobressart).
As in Experiment 1, we used entropy and conditional entropy to measure the information content of the available predictors and added the entropy of both a uniform and the observed distribution of ground rainfall as benchmarks. The results are shown in Table 3. As the results for the two stations are similar, we mainly discuss Petit-Nobressart in the following, moving from the remotest and presumably least informative predictor to the closest.
Table 3Entropy of the target (RR0) and the benchmark distribution (RR0 uniform), conditional entropies of the target given various predictors along the radar path, non-normalized and normalized, for Petit-Nobressart and Useldange, respectively. Underlying data are from the filtered data set. Predictors are ordered by decreasing distance to the target.
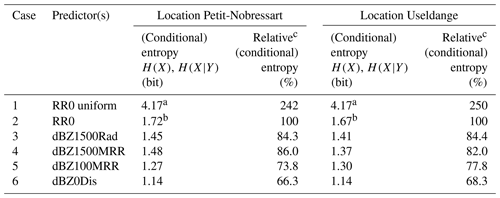
a Unconditional entropy of the benchmark uniform distribution; b Unconditional entropy of the target; c H(RR0|predictor)∕(RR0) ⋅ 100.
Weather radar data, even if they are measured at distance and at height contain considerable information about ground rainfall: using them as predictors reduced uncertainty by 15.7 % (100 % to 84.3 %) compared with the benchmark entropy of the target distribution (Table 3, cases 2 and 3). This is comparable to the outcomes of Experiment 1 based on all sites (15.3 %, Table 2, same cases). We expected MRR observations taken at the same site and elevation to be more informative than their weather radar pendant, because the MRR signal path, and with it the potential for signal corruption, is considerably shorter. However, this is not clearly evident from the results: at Useldange the use of MRR instead of weather radar data additionally reduced uncertainty by only 2.4 % (84.4 % to 82.0 %, Table 3, cases 3 and 4), and at Petit-Nobressart they were even less informative (86.0 % instead of 84.4 %, Table 3, same cases). These results should be interpreted with some care due to the relatively limited data base; however, it seems safe to conclude that there is no large difference in the information content of MRR and weather radar observations taken at height.
So why go to the extra trouble of operating an MRR? The advantages of this instrument are evident when moving down to elevations inaccessible by weather radar. Changes in drop size distribution along the pathway of rainfall from cloud to ground can be considerable, and the closer to the ground the observation is taken the stronger its relation to ground rainfall: using MRR data from the lowermost bin (≤100 m above ground) reduced uncertainty by 12.2 % compared with using the uppermost bin (86.0 % to 73.8 %, Table 3, cases 4 and 5). This emphasizes the importance of VPR correction when using weather radar data (Vignal et al., 1999, 2000). Based on these results, an obvious next step would be to derive VPR corrections from the two MRRs and investigate the information gain when applied to other sites in the domain; however, for the sake of brevity, we leave this for future studies.
Further information gains can be achieved when measuring reflectivity directly at the ground: using the disdrometer measurements further reduced uncertainty by 7.5 % (73.8 % to 66.3 %, Table 3, cases 5 and 6), compared with the MRR observations. This gain is not only due to using ground observations, which completely excludes any negative VPR effects, but also because predictor and target data were observed at the same spot and by the same sensor. Seen from this perspective, it is surprising that considerable uncertainty still remains (66.3 % of the benchmark uncertainty, Table 3, cases 6 and 2), which must be attributed to the ambiguous relationship between radar reflectivity and rain rate due to the natural variability of drop size distribution.
3.6 Experiment 6: QPE based on radar and rain gauge data
In this final experiment we compare two methods of QPE, radar-based and rain-gauge-based, and additionally explore the benefits of jointly tapping both sources of information. As we were not dependent on the availability of MRR data as in the previous experiment, we could again make use of the full eight-site set of observations filtered with the “minimum precipitation” filter.
We used the same data-based approach of constructing empirical dpd's as a predictive model as in all previous experiments; the only difference between the three tested QPE models was the type of predictor used: for the radar-based QPE, we used weather radar observations at 1500 m above ground in a one-predictor model to predict ground rainfall at the same site. This is the same approach that we applied in Experiment 1. For the rain-gauge-based QPE, we built a one-predictor model based on a straightforward approach comparable to leave-one-out cross validation: each of the eight available stations (see Fig. 2 and Table 1) was once used as a target station, and observations from each of the remaining seven stations were used separately as predictors. This way we could calculate the information content in the predictor as a function of the distance between stations. Eight stations render a total of 56 unique station pairings; for our stations, the minimum, average and maximum distances were 1.9, 7.2 and 15.3 km, respectively. For later plotting, we binned the results in seven distance classes with a respective 2 km width and took averages within each bin. This is comparable to using range bins when calculating a semivariogram.
For the joint QPE model we extended the approach used for rain gauge interpolation to a two-predictor model: again each of the eight available stations was used once as a target station; however, in this case, not only were observations from each of the respective remaining stations used as predictors, but radar observations measured at height above the target station were also applied. This is a typical approach when merging radar and rain gauge data for QPE: we use data from rain gauges observed at a horizontal distance from the target, and radar data observed at a vertical distance from the target.
As we built and compared models with different numbers of predictors in this experiment, and as the models for each particular target station were built from a subset of the data only, it could be worthwhile exploring the additional uncertainty due to the effect of sample size here as in experiments 2 and 3. However, for this particular experiment we found it more useful for the reader (and us) to discuss results as a function of the distance between stations, as it provides a link to the large body of literature on spatial rainfall structure analysis and station-based rainfall interpolation. The results are shown in Fig. 7.
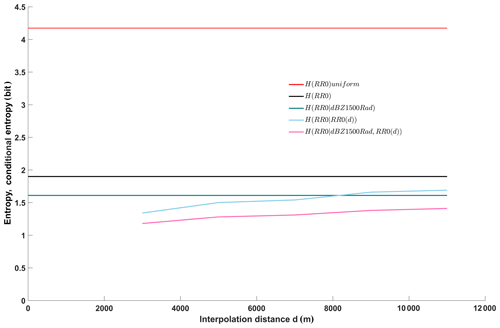
Figure 7Entropy of the unconditional, target distribution (filtered data set, black line, same as in Fig. 4); entropy of the benchmark uniform distribution (filtered data set, red line, same as in Fig. 4); conditional entropy of the target given reflectivity as predictor (green line); conditional entropy of the target given station rain rate observations as a function of interpolation distance (light blue line); and conditional entropy of the target given reflectivity and rain rate at stations as a predictor as a function of interpolation distance (pink line). Underlying data are from the filtered data set.
Just as in Figs. 4 and 5, we included the benchmark unconditional entropies of the target for a maximum entropy uniform distribution (red line) and the observed distribution of all stations combined (black line) to put the results into perspective. As the radar-only model (green line) is independent of any interpolation distance, simply because it does not make use of any station data, it plots as a horizontal line. Its conditional entropy (1.61 bit) corresponds to the right-hand (full-size sample) value of the green line in Fig. 4, and to case 3 in Table 2.
However, for the QPE model based on rain gauge observations (light blue line), the interpolation distance does play a role: as is to be expected, the smaller the distance between the target and the predictor station, the higher the information content of the predictor and the smaller the conditional entropy, i.e., the blue line rises from left to right. For short distances between 2 and 4 km, conditional entropy is 1.34 bit, which is lower than for the radar-only QPE. If we take the unconditional entropy of the target again as a reference as in Experiment 1 (Table 1, case 2), station-only QPE for short distances reduces uncertainty to 70.5 %, and radar-only reduces uncertainty to 84.7 %. For long distances, however, this order is reversed, and station-only QPE only reduces uncertainty to 1.69 bit or 88.9 % of the reference. The break-even point at which both methods perform equally well lies at a station distance of about 8 km. This means that if we were asked to choose one of the two models for QPE, the best choice would be to use station interpolation for all targets within less than about 8 km from the nearest station, and radar-QPE for all others.
The above results indicate that each of the two QPE methods has its particular strengths. In other words they add nonredundant information; therefore, we can expect some benefits when joining them in a two-predictor model. This is indeed the case if we take a look at the related conditional entropies plotted as the pink line in Fig. 7. While it resembles the plot of the station-only model in overall shape and trend, it is shifted downward: conditional entropy for short distances is now reduced to only 1.18 bit (62.1 % of the reference), and even for the longest distances (1.41 bit = 74.2 % of the reference) it is still smaller than both the station-only and the radar-only values. Interestingly, in the combined model the radar observations add information – even for small station distances. We assume that this can be attributed to convective rainfall situations, where strong spatial rainfall heterogeneity occurs, unresolvable even by rain gauges only a few kilometers apart.
In Experiment 1 we also built and tested two-predictor models. The best among them, using radar data and tenner-days of the year for predictors (Table 1, case 11), reduced conditional entropy to 77.4 % of the reference. While this is a considerable improvement, it is surpassed by the radar–rain gauge model even for the largest station distance. Obviously, ground rainfall and radar observations contain nonredundant information which, when used together, have a large potential to improve QPE.
Reliable QPE is an important prerequisite for many hydrometeorological design and management purposes. In this context we pursued two aims with this paper: the first was to suggest and demonstrate a probabilistic framework based on concepts of information theory, in which predictive relations are expressed by empirical discrete probability distributions directly derived from data. The framework allows for the integration of any kind of data deemed useful and explicitly acknowledges the uncertain nature of QPE. The second aim was to investigate the information gains and losses associated with various data and practices typically applied in QPE. For this purpose we conducted a total of six experiments using a comprehensive set of data comprising 4 years of hourly aggregated observations from weather radar, vertical radar (MRR), disdrometers, rain gauges and a range of operationally available hydrometeorological observables, such as large-scale circulation patterns, ground meteorological variables and season indicators.
In Experiment 1, we measured the information on ground rainfall contained in various operationally available predictors with entropy and conditional entropy. Weather radar proved to be the single-most important source of information, which could be further improved by distinguishing Z–R relationships by season and prevailing circulation pattern.
In Experiment 2, we tested the robustness of QPE models developed in the previous experiment by measuring the additional uncertainty due to limited learning data with Kullback–Leibler divergence and cross entropy. The main lesson learned here was that this added uncertainty is strongly dependent on the number of predictors used in the model, and that for unfavorable constellations (multiple-predictor models learning from small samples) this effect quickly dominates total uncertainty: this is the well-known “curse of dimensionality”. For the data set used in this study, we found a two-predictor model using a month-specific relation between radar reflectivity and ground rainfall to provide the best trade-off between performance and robustness.
In Experiment 3, we examined the degree to which the empirical Z–R relationship in the test domain varies in space, and the data set sizes that are required to support the use of site-specific Z–R relations. Overall, the information gain of site-specific Z–R relations was smaller than when distinguishing them according to season or circulation pattern as we did in the previous experiments. Moreover, applying site-specific Z–R relations instead of a single, site-independent relation means adding another predictor to the QPE model, which in turn mean that we increase the curse of dimensionality. In fact, more than half of the available data had to be used for learning the site-specific model before the additional effort paid off. The conclusion here was to stick to a site-independent relation, which also seems reasonable from a meteorological point of view due to the relatively small extent of the test domain (288 km2).
In Experiment 4, we evaluated the effect of functional compression, i.e., the information loss when replacing the data-inherent probabilistic relationship between reflectivity and rain rate by a deterministic functional approximation. We measured the additional uncertainty with Kullback–Leibler divergence, which adds to the uncertainty caused by the incomplete information of the predictor regarding the target measured by conditional entropy. We used two standard power-law Z–R relations: the well-known Marshall–Palmer relation, and a modified version thereof with optimized function parameters. For both, the added uncertainty was of the order of 60 % of total uncertainty. While these numbers may vary with the chosen binning resolution, compression of probabilistic data relationships to deterministic functions will invariably increase uncertainty as long as learning and application of data relations is carried out on the same data set.
In Experiment 5, we investigated information gains along the radar path using weather radar, MRR and disdrometer data from two sites. The main insights here were that the information content of radar reflectivity measured at height (1500 m above ground) does not differ much between weather radar and MRR, but considerable additional information is gained by using observations from lower elevations (100 m above ground), thereby avoiding information losses due to changes in drop size spectra along the pathway of precipitation from cloud to ground. This emphasizes both the importance of VPR corrections for accurate QPE and of the required MRR observations. Despite these information gains, considerable uncertainty remained even when using as predictor reflectivity observations taken at the same spot and by the same device (disdrometer) as the target variable (rain rate) itself. This indicates a somewhat ambiguous relationship between radar reflectivity and rain rate as measured by the disdrometer, which could potentially be sharpened by taking the precipitation type into account.
In the last experiment, Experiment 6, we built QPE models based on radar data only, rain gauge data only and a combination thereof and evaluated their information content as a function of the distance between the target and predictor rain gauge. Comparing the first two revealed that a separation distance of ∼8 km marks a transition: for shorter distances, gauge-based QPE is superior, for longer distances radar-based QPE is more appropriate. Combining the two in a two-predictor QPE model, however, not only outperformed both of them for all separation distances, but also rivaled radar-based two-predictor models applying season or circulation pattern. For rain gauge networks comparable in coverage and density to the one used in this study, rain gauge and radar data apparently contain useful, nonredundant information which should be jointly exploited.
We would like to emphasize that the results from these experiments are partly contingent on the choice of the data filter: the “minimum precipitation” (at least two rain gauges with rainfall ≥ 0.5 mm h−1) filter we applied excluded all cases where rainfall occurred at only a single station, and it also excluded all cases of widespread but very low-intensity rain.
Quantitative statements about the information content of particular predictors or the relative performance of competing QPE models may differ according to these user choices. However, we would like to point out that all of the different experiments in this study could be formulated, conducted and evaluated in a single framework and relied on a single property – information. Therefore, it is not so much the particular results we want to emphasize here, but rather the probabilistic, data- and information-based framework we applied. By its probabilistic concept, it explicitly acknowledges the uncertain nature of QPE, and by expressing probabilities in terms of information, it facilitates both interpretation and computation. In this framework, predictive relationships are directly derived from data and are expressed as discrete probability distributions. The advantage of this is that this avoids the introduction of unwanted side information as much as possible, e.g., by parametric choices, and it avoids the deletion of existing information, e.g., by data transformation or lossy compression. Altogether, this facilitates tracking sources and sinks of information. However, these advantages come at a price: learning robust data-based relations requires a considerable amount of available target and predictor data, and applying them for predictions is computationally more expensive than using deterministic functions.
The reflectivity and rain rate data measured by the six disdrometers and two MRRs are published by the GFZ data service repository (Neuper and Ehret, 2018). The rain gauge data from Roodt station and the rain gauge data, the 2 m temperature data, the relative humidity and the wind data from Useldange station are publicly available from the Administration des services techniques de l'agriculture ASTA at http://www.agrimeteo.lu/ (last access: 4 December 2018). The rain gauge data from the Reichlange station were provided upon request by the Hydrometry Service Luxembourg (https://www.inondations.lu/; last access: 4 December 2018). The sounding data from which CAPE were calculated are publicly available from the University of Wyoming at http://weather.uwyo.edu/upperair/sounding.html (last access: 4 December 2018). The data of the objective classification of the prevailing circulation pattern over Europe model are publicly available from the German Weather Service at https://www.dwd.de/DE/leistungen/wetterlagenklassifikation/wetterlagenklassifikation.html (last access: 4 December 2018). The raw reflectivity volume radar data from the single polarization C-band Doppler radar located in Neuheilenbach are available upon request from the German Weather Service (DWD). The code used to conduct all analyses in this paper is publicly available at https://github.com/KIT-HYD/Radar-based-QPE-using-information-measures (last access: 20 August 2019).
UE and MN directly contributed to the conception and design of the work, collected and processed the various data sets, conducted a thorough data quality control, undertook the data analysis and interpretation, and wrote the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Linking landscape organisation and hydrological functioning: from hypotheses and observations to concepts, models and understanding (HESS/ESSD inter-journal SI)”. It is not associated with a conference.
We acknowledge support from the Deutsche Forschungsgemeinschaft (DFG) and the Open Access Publishing Fund of Karlsruhe Institute of Technology (KIT). This research contributes to the “Catchments As Organized Systems” (CAOS) research group funded by the DFG. We gratefully acknowledge the fruitful cooperation and joint operation of the meteorological observation network within CAOS, namely Hans-Stefan Bauer and Volker Wulfmeyer. We also gratefully acknowledge the providers of meteorological data used in this study: the German Weather Service (DWD) for radar and classified circulation pattern data, the Administration des services techniques de l'agriculture (ASTA) for rain gauge and climate data and the Hydrometry Service Luxembourg for rain gauge data. Furthermore, we especially thank Jean-François Iffly from the Luxembourg Institute of Science and Technology (LIST) for his extensive commitment to finding the right locations to place the instruments and his outstanding help with maintaining them. We further thank Kirsten Elger from GFZ Helmholtz Centre Potsdam for her patient help regarding data publication in the GFZ repository; our colleagues Ralf Loritz, Sibylle Haßler, Conrad Jackisch and Erwin Zehe for fruitful discussions on data analysis; and Jan Handwerker from the KIT Institute of Meteorology and Climate Research for help concerning radar meteorology issues. Last but not least, we thank the rest of the CAOS team for the warm-hearted project meetings and discussions.
The article processing charges for this open-access publication were covered by a Research Centre of the Helmholtz Association.
This paper was edited by Alexander Gelfan and reviewed by two anonymous referees.
Adirosi, E., Volpi, E., Lombardo, F., and Baldini, L.: Raindrop size distribution: Fitting performance of common theoretical models, Adv. Water Resour., 96, 290–305, https://doi.org/10.1016/j.advwatres.2016.07.010, 2016. a
Atlas, D., Srivastava, R., and Sekhon, R. S.: Doppler radar characteristics of precipitation at vertical incidence, Rev. Geophys., 11, 1–35, https://doi.org/10.1029/RG011i001p00001, 1973. a
Battan, L. J.: Radar Meteorology, The University of Chicago Press, Chicago, 1959a. a
Battan, L. J.: Radar Observations of the Atmosphere, The University of Chicago Press, Chicago, 1959b. a, b
Bauer, H.-S., Schwitalla, T., Wulfmeyer, V., Bakhshaii, A., Ehret, U., Neuper, M., and Caumont, O.: Quantitative precipitation estimation based on high-resolution numerical weather prediction and data assimilation with WRF – a performance test, Tellus A, 67, 25047, https://doi.org/10.3402/tellusa.v67.25047, 2015. a
Bronstert, A., Agarwal, A., Boessenkool, B., Fischer, M., Heistermann, M., Köhn, L., Moran, T., and Wendi, D.: The Braunsbach Flashflood of Mai 29th, 2016-Origin, Pathways and Impacts of an Extreme Hydro-Meteorological Event. Part 1: Meteorological and Hydrological Analysis, Hydrol. Wasserbewirt., 61, 150–162, https://doi.org/10.5675/HyWa_2017,3_1, 2017. a
Brunsell, N.: A multiscale information theory approach to assess spatial–temporal variability of daily precipitation, J. Hydrol., 385, 165–172, 2010. a
Bückle, J.: Korrektur von Second Trip Echos in Radardaten, Diploma thesis, Institute of Meteorology and Climate Research, University of Karlsruhe, Karlsruhe, 2009. a
Bunkers, M. J., Johnson, J. S., Czepyha, L. J., Grzywacz, J. M., Klimowski, B. A., and Hjelmfelt, M. R.: An observational examination of long-lived supercells. Part II: Environmental conditions and forecasting, Weather Forecast., 21, 689–714, https://doi.org/10.1175/WAF952.1, 2006. a
Cao, Q., Zhang, G., Brandes, E. A., and Schuur, T. J.: Polarimetric radar rain estimation through retrieval of drop size distribution using a Bayesian approach, J. Appl. Meteorol. Clim., 49, 973–990, https://doi.org/10.1175/2009jamc2227.1, 2010. a
Cecinati, F., de Niet, A., Sawicka, K., and Rico-Ramirez, M.: Optimal temporal resolution of rainfall for urban applications and uncertainty propagation, Water, 9, 762, https://doi.org/10.3390/w9100762, 2017a. a
Cecinati, F., Rico-Ramirez, M. A., Heuvelink, G. B., and Han, D.: Representing radar rainfall uncertainty with ensembles based on a time-variant geostatistical error modelling approach, J. Hydrol., 548, 391–405, https://doi.org/10.1016/j.jhydrol.2017.02.053, 2017b. a
Cover, T. M. and Thomas, J. A.: Elements of information theory, John Wiley & Sons, New York, 1991. a, b
Darscheid, P., Guthke, A., and Ehret, U.: A maximum-entropy method to estimate discrete distributions from samples ensuring nonzero probabilities, Entropy, 20, 601, https://doi.org/10.5445/IR/1000085954, 2018. a, b
Diem, M.: Zur Struktur der Niederschläge III – Regen in der arktischen, gemäßigten und tropischen Zone, Arch. Meteorol. Geophys. Bioklimatol. Ser. B, 16, 347–390, https://doi.org/10.1007/BF02243180, 1968. a
Dittmann, E., Barth, S., Lang, J., and Müller-Westermeier, G.: Objektive Wetterlagenklassifikation, Berichte des Deutschen Wetterdienstes (DWD), Selbstverlag des Deutschen Wetterdienstes, Offenbach am Main, 1995. a
Dotzek, N. and Beheng, K. D.: The influence of deep convective motions on the variability of Z–R relations, Atmos. Res., 59, 15–39, https://doi.org/10.1016/S0169-8095(01)00107-7, 2001. a
Doviak, R. J. and Zrnic, D. S.: Doppler Radar and Weather Observations, Academic Press, San Diego, 1993. a, b
Ehret, U., Gupta, H. V., Sivapalan, M., Weijs, S. V., Schymanski, S. J., Blöschl, G., Gelfan, A. N., Harman, C., Kleidon, A., Bogaard, T. A., Wang, D., Wagener, T., Scherer, U., Zehe, E., Bierkens, M. F. P., Di Baldassarre, G., Parajka, J., van Beek, L. P. H., van Griensven, A., Westhoff, M. C., and Winsemius, H. C.: Advancing catchment hydrology to deal with predictions under change, Hydrol. Earth Syst. Sci., 18, 649–671, https://doi.org/10.5194/hess-18-649-2014, 2014. a
Faber, R.: Climatologie du Grand-Duché de Luxembourg, Publication du Musée national d'histoire naturelle et de la Société des naturalistes luxembourgeois, Graphic Center Bourg-Bourger, Luxembourg, 1971. a
Fabry, F.: Radar Meteorology – Principles and Practice, Cambridge University Press, Cambridge, 2015. a
Friedrich, K., Higgins, S., Masters, F. J., and Lopez, C. R.: Articulating and stationary PARSIVEL disdrometer measurements in conditions with strong winds and heavy rainfall, J. Atmos. Ocean. Tech., 30, 2063–2080, https://doi.org/10.1175/JTECH-D-12-00254.1, 2013a. a
Friedrich, K., Kalina, E. A., Masters, F. J., and Lopez, C. R.: Drop-size distributions in thunderstorms measured by optical disdrometers during VORTEX2, Mon. Weather Rev., 141, 1182–1203, https://doi.org/10.1175/MWR-D-12-00116.1, 2013b. a
Germann, U., Galli, G., Boscacci, M., and Bolliger, M.: Radar precipitation measurement in a mountainous region, Q. J. Roy. Meteorol. Soc., 132, 1669–1692, https://doi.org/10.1256/qj.05.190, 2006. a
Gong, W., Yang, D., Gupta, H. V., and Nearing, G.: Estimating information entropy for hydrological data: One-dimensional case, Water Resour. Res., 50, 5003–5018, https://doi.org/10.1002/2014wr015874, 2014. a
Goudenhoofdt, E. and Delobbe, L.: Evaluation of radar-gauge merging methods for quantitative precipitation estimates, Hydrol. Earth Syst. Sci., 13, 195–203, https://doi.org/10.5194/hess-13-195-2009, 2009. a
Goudenhoofdt, E., Delobbe, L., and Willems, P.: Regional frequency analysis of extreme rainfall in Belgium based on radar estimates, Hydrol. Earth Syst. Sci., 21, 5385–5399, https://doi.org/10.5194/hess-21-5385-2017, 2017. a
Hagen, M. and Yuter, S. E.: Relations between radar reflectivity, liquid-water content, and rainfall rate during the MAP SOP, Q. J. Roy. Meteorol. Soc., 129, 477–493, https://doi.org/10.1256/qj.02.23, 2003. a
Hannesen, R.: Analyse konvektiver Niederschlagssysteme mit einem C-Band Dopplerradar in orographisch gegliedertem Gelände, Dissertation, Institute of Meteorology and Climate Research, University of Karlsruhe, Karlsruhe, 1998. a
Huff, F.: Sampling errors in measurement of mean precipitation, J. Appl. Meteorol., 9, 35–44, https://doi.org/10.1175/1520-0450(1970)009<0035:SEIMOM>2.0.CO;2, 1970. a
Joss, J., Waldvogel, A., and Collier, C.: Precipitation measurement and hydrology, in: Radar in Meteorology, edited by: Atlas, D., Amer. Meteor. Soc., Boston, MA, 577–606, 1990. a
Kirstetter, P.-E., Gourley, J. J., Hong, Y., Zhang, J., Moazamigoodarzi, S., Langston, C., and Arthur, A.: Probabilistic precipitation rate estimates with ground-based radar networks, Water Resour. Res., 51, 1422–1442, https://doi.org/10.1002/2014WR015672, 2015. a, b
Knuth, K. H.: Optimal data-based binning for histograms, arXiv:preprint/physics/0605197v2 [physics.data-an], 2013. a
Köppen, W. and Geiger, R.: Handbuch der Klimatologie: Band 1, Teil C: Das geographische System der Klimate, Gebruder Borntraeger, Berlin, 1930. a
Kronenberg, R., Franke, J., and Bernhofer, C.: Classification of daily precipitation patterns on the basis of radar-derived precipitation rates for Saxony, Germany, Meteorol. Z., 21, 475–486, https://doi.org/10.1127/0941-2948/2012/0343, 2012. a
Kullback, S. and Leibler, R. A.: On information and sufficiency, Ann. Math. Stat., 22, 79–86, 1951. a
Lee, G. W. and Zawadzki, I.: Variability of drop size distributions: Time-scale dependence of the variability and its effects on rain estimation, J. Appl. Meteorol., 44, 241–255, https://doi.org/10.1175/JAM2183.1, 2005. a
Löffler-Mang, M. and Joss, J.: An optical disdrometer for measuring size and velocity of hydrometeors, J. Atmos. Ocean. Tech., 17, 130–139, https://doi.org/10.1175/1520-0426(2000)017<0130:aodfms>2.0.co;2, 2000. a
Löffler-Mang, M., Kunz, M., and Schmid, W.: On the performance of a low-cost K-band Doppler radar for quantitative rain measurements, J. Atmos. Ocean. Tech., 16, 379–387, https://doi.org/10.1175/1520-0426(1999)016<0379:otpoal>2.0.co;2, 1999. a
Loritz, R., Gupta, H., Jackisch, C., Westhoff, M., Kleidon, A., Ehret, U., and Zehe, E.: On the dynamic nature of hydrological similarity, Hydrol. Earth Syst. Sci., 22, 3663–3684, https://doi.org/10.5194/hess-22-3663-2018, 2018. a
Marshall, J. and Palmer, W.: The Distribution of Raindrops with Size, J. Meteorol., 5, 165–166, 1948. a, b, c
Nearing, G. S., Tian, Y., Gupta, H. V., Clark, M. P., Harrison, K. W., and Weijs, S. V.: A philosophical basis for hydrological uncertainty, Hydrolog. Sci. J., 61, 1666–1678, https://doi.org/10.1080/02626667.2016.1183009, 2016. a
Nešpor, V. and Sevruk, B.: Estimation of wind-induced error of rainfall gauge measurements using a numerical simulation, J. Atmos. Ocean. Tech., 16, 450–464, https://doi.org/10.1175/1520-0426(1999)016<0450:EOWIEO>2.0.CO;2, 1999. a
Neuper, M.: Anomale Strahlausbreitung – Prinzip und Fallbeispiele, Seminar work, Institute of Meteorology and Climate Research, University of Karlsruhe, Karlsruhe, 2009. a
Neuper, M. and Ehret, U.: CAOS rain rate and reflectivity data set of 6 disdrometres and 2 micro rain radars at 3 different heights at 6 stations in the Attert catchment, Luxembourg from Oct 2012–Sept 2016, GFZ German Research Centre for Geosciences, Potsdam, Germany, https://doi.org/10.5880/FIDGEO.2018.070, 2018. a
Nystuen, J. A.: Relative performance of automatic rain gauges under different rainfall conditions, J. Atmos. Ocean. Tech., 16, 1025–1043, https://doi.org/10.1175/1520-0426(1999)016<1025:RPOARG>2.0.CO;2, 1999. a
Overeem, A., Holleman, I., and Buishand, A.: Derivation of a 10-year radar-based climatology of rainfall, J. Appl. Meteorol. Clim., 48, 1448–1463, https://doi.org/10.1175/2009jamc1954.1, 2009. a
Pechlivanidis, I. G., Jackson, B., Mcmillan, H., and Gupta, H. V.: Robust informational entropy-based descriptors of flow in catchment hydrology, Hydrolog. Sci. J., 61, 1–18, https://doi.org/10.1080/02626667.2014.983516, 2016. a
Peters, G., Fischer, B., and Andersson, T.: Rain observations with a vertically looking Micro Rain Radar (MRR), Boreal Environ. Res., 7, 353–362, 2002. a
Peters, G., Fischer, B., Münster, H., Clemens, M., and Wagner, A.: Profiles of raindrop size distributions as retrieved by microrain radars, J. Appl. Meteorol., 44, 1930–1949, https://doi.org/10.1175/JAM2316.1, 2005. a
Pfister, L., Humbert, J., and Hoffmann, L.: Recent trends in rainfall-runoff characteristics in the Alzette river basin, Luxembourg, Climatic Change, 45, 323–337, https://doi.org/10.1023/A:1005567808533, 2000. a
Pfister, L., Wagner, C., Vansuypeene, E., Drogue, G., and Hoffmann, L.: Atlas climatique du grand-duché de Luxembourg, Luxembourg: Musée National d'Histoire Naturelle, Société des naturalistes luxembourgeois, Centre de Recherche Public, edited by: Ries, C. and Lippmann, G., Administration des Services Techniques de l'Agriculture, Luxembourg, 2005. a
Rauber, R. M. and Nesbitt, S. L.: Radar Meteorology: A First Course, John Wiley & Sons, Hoboken, NJ, 2018. a
Rinehart, R.: Radar for Meteorologists, Univ. North Dakota, Grand Forks, USA, 1991. a
Rossa, A., Bruen, M., Fruehwald, D., Macpherson, B., Holleman, I., Michelson, D., and Michaelides, S.: COST 717 action–use of radar observation in hydrology and NWP models, European Co-Operation in the Field of Scientific and Technical Research, Brussels, 292 pp., 2005. a
Ruiz-Villanueva, V., Borga, M., Zoccatelli, D., Marchi, L., Gaume, E., and Ehret, U.: Extreme flood response to short-duration convective rainfall in South-West Germany, Hydrol. Earth Syst. Sci., 16, 1543–1559, https://doi.org/10.5194/hess-16-1543-2012, 2012. a
Sauvageot, H. R.: Radar Meteorology, Artech House, Boston, 1992. a, b
Schmithüsen, J.: Das Luxemburger Land: Landesnatur, Volkstum und bäuerliche Wirtschaft, in: vol. 34, Verlag von S. Hirzel, Leipzig, 1940. a
Seifert, A. and Beheng, K.: A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 2: Maritime vs. continental deep convective storms, Meteorol. Atmos. Phys., 92, 67–82, https://doi.org/10.1007/s00703-005-0113-3, 2006. a
Shannon, C. E.: A mathematical theory of communication, Bell Syst. Tech. J., 27, 379–423, 1948. a
Sharma, A. and Mehrotra, R.: An information theoretic alternative to model a natural system using observational information alone, Water Resour. Res., 50, 650–660, https://doi.org/10.1002/2013WR013845, 2014. a
Singh, V. P.: Entropy Theory and its Application in Environmental and Water Engineering, John Wiley & Sons, Chichester, West Sussex, UK, 2013. a
Thiesen, S., Darscheid, P., and Ehret, U.: Identifying rainfall-runoff events in discharge time series: a data-driven method based on information theory, Hydrol. Earth Syst. Sci., 23, 1015–1034, https://doi.org/10.5194/hess-23-1015-2019, 2019. a
Thorndahl, S., Einfalt, T., Willems, P., Nielsen, J. E., ten Veldhuis, M.-C., Arnbjerg-Nielsen, K., Rasmussen, M. R., and Molnar, P.: Weather radar rainfall data in urban hydrology, Hydrol. Earth System Sci., 21, 1359–1380, https://doi.org/10.5194/hess-21-1359-2017, 2017. a
Todini, E.: Hydrological catchment modelling: past, present and future, Hydrol. Earth Syst. Sci., 11, 468–482, https://doi.org/10.5194/hess-11-468-2007, 2007. a
Ulbrich, C. W. and Atlas, D.: Rainfall microphysics and radar properties: Analysis methods for drop size spectra, J. Appl. Meteorol., 37, 912–923, https://doi.org/10.1175/1520-0450(1998)037<0912:RMARPA>2.0.CO;2, 1998. a
Vasquez, T.: Instability, Skew-T & Hodograph Handbook, Weather Graphics Technologies, Garland, TX, 2017. a
Vignal, B., Andrieu, H., and Creutin, J. D.: Identification of vertical profiles of reflectivity from volume scan radar data, J. Appl. Meteorol., 38, 1214–1228, https://doi.org/10.1175/1520-0450(1999)038<1214:IOVPOR>2.0.CO;2, 1999. a, b
Vignal, B., Galli, G., Joss, J., and Germann, U.: Three methods to determine profiles of reflectivity from volumetric radar data to correct precipitation estimates, J. Appl. Meteorol., 39, 1715–1726, https://doi.org/10.1175/1520-0450-39.10.1715, 2000. a, b
Villarini, G. and Krajewski, W. F.: Review of the different sources of uncertainty in single polarization radar-based estimates of rainfall, Surv. Geophys., 31, 107–129, https://doi.org/10.1007/s10712-009-9079-x, 2010. a
Wang, L., Ochoa-Rodriguez, S., Onof, C., and Willems, P.: Singularity-sensitive gauge-based radar rainfall adjustment methods for urban hydrological applications, Hydrol. Earth Syst. Sci., 19, 4001–4021, https://doi.org/10.5194/hess-19-4001-2015, 2015. a, b
Weijs, S. V.: Information theory for risk-based water system operation, Phd thesis, Faculty of Civil Engineering & Geosciences, section Water Resources Management, TU Delft, Delft, the Netherlands, 2011. a, b
Wellmann, J. F. and Regenauer-Lieb, K.: Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models, Tectonophysics, 526, 207–216, https://doi.org/10.1016/j.tecto.2011.05.001, 2012. a
Yang, D., Elomaa, E., Tuominen, A., Aaltonen, A., Goodison, B., Gunther, T., Golubev, V., Sevruk, B., Madsen, H., and Milkovic, J.: Wind-induced precipitation undercatch of the Hellmann gauges, Hydrol. Res., 30, 57–80, https://doi.org/10.2166/nh.1999.0004, 1999. a
Yang, X., Kuang, Q., Zhang, W., and Zhang, G.: A terrain-based weighted random forests method for radar quantitative precipitation estimation, Meteorol. Appl., 24, 404–414, https://doi.org/10.1002/met.1638, 2017. a
Zawadzki, I.: Factors affecting the precision of radar measurements of rain, in: Preprints 22nd Int. Conf. on Radar Meteorology, Amer. Meteor. Soc., Zürich, Switzerland, 251–256, 1984. a
Zehe, E., Ehret, U., Pfister, L., Blume, T., Schröder, B., Westhoff, M., Jackisch, C., Schymanski, S. J., Weiler, M., Schulz, K., Allroggen, N., Tronicke, J., van Schaik, L., Dietrich, P., Scherer, U., Eccard, J., Wulfmeyer, V., and Kleidon, A.: HESS Opinions: From response units to functional units: a thermodynamic reinterpretation of the HRU concept to link spatial organization and functioning of intermediate scale catchments, Hydrol. Earth Syst. Sci., 18, 4635–4655, https://doi.org/10.5194/hess-18-4635-2014, 2014. a
Zhang, G., Vivekanandan, J., and Brandes, E.: A method for estimating rain rate and drop size distribution from polarimetric radar measurements, IEEE T. Geosci. Remote, 39, 830–841, 2001. a