A partially coupled hydro-mechanical analysis of the Bengal Aquifer System under hydrological loading

The coupled poro-mechanical behaviour of geologic-fluid systems is fundamental to numerous processes in structural geology, seismology, and geotechnics, but is frequently overlooked in hydrogeology. Substantial poro-mechanical influences on groundwater head have recently been highlighted in the Bengal Aquifer System, however, driven by terrestrial water loading across the Ganges–Brahmaputra–Meghna floodplains. Groundwater management in this strategically important fluvio-deltaic aquifer, the largest in southern Asia, requires a coupled hydro-mechanical approach which acknowledges poroelasticity. We present a simple partially coupled, 1-D poroelastic model of the Bengal Aquifer System, and explore the poro-mechanical responses of the aquifer to surface boundary conditions representing hydraulic head and mechanical load under three modes of terrestrial water variation. The characteristic responses, shown as amplitude and phase of hydraulic head in depth profile and of ground surface deflection, demonstrate (i) the limits to using water levels in piezometers to indicate groundwater recharge, as conventionally applied in groundwater resources management; (ii) the conditions under which piezometer water levels respond primarily to changes in the mass of terrestrial water storage, as applied in geological weighing lysimetry; (iii) the relationship of ground surface vertical deflection with changes in groundwater storage; and (iv) errors of attribution that could result from ignoring the poroelastic behaviour of the aquifer. These concepts are illustrated through application of the partially coupled model to interpret multi-level piezometer data at two sites in southern Bangladesh. There is a need for further research into the coupled responses of the aquifer due to more complex forms of surface loading, particularly from rivers.

1 Introduction

Throughout the Bengal Basin, the floodplains of the Ganges, Brahmaputra, and Meghna (GBM) rivers (Fig. 1) are underlain by the Bengal Aquifer System (BAS), the largest aquifer in southern Asia and the source of water to over 100 million people (Burgess et al., 2010). More than 10 million tubewells throughout the basin provide water from the BAS for domestic use and for irrigation of the rice crop (Ravenscroft et al., 2009); these include hand-pumped tubewells, normally between 15 and 30 m depth below ground level (b.g.l.), for domestic use, and tubewells installed with motor-driven pumps to abstract water from between 50 and 75 m depth b.g.l. for irrigation of the dry season rice crop (January to April). Municipal water supplies commonly abstract year-round from depths between 200 and 300 m b.g.l. (Shamsudduha et al., 2018). Management of the BAS groundwater resource relies on monitoring water levels in networks of observation boreholes, taking the conventional approach that changes in groundwater heads represent volumetric changes in groundwater storage through recharge and drainage (Shamsudduha et al., 2011). This approach presumes the hydraulic behaviour of the aquifer to be decoupled from its mechanical response to changes in stress. Recently, however, the distinctively poroelastic behaviour of the BAS has been recognized (Burgess et al., 2017), by which groundwater heads are subject to substantial mechanical perturbation driven by changes in the mass of terrestrial water storage (TWS) above the surface of the aquifer. A coupled hydro-mechanical approach is necessary for understanding groundwater conditions and managing resources in this environment, particularly in relation to recharge (Shamsudduha et al., 2012), sustainability of groundwater abstraction for irrigation (Shamsudduha et al., 2011) and municipal water supply (Ravenscroft et al., 2013), and the security of schemes for mitigation against groundwater arsenic (Michael and Voss, 2008) and salinity (Rahman et al., 2011; Sultana et al., 2015).

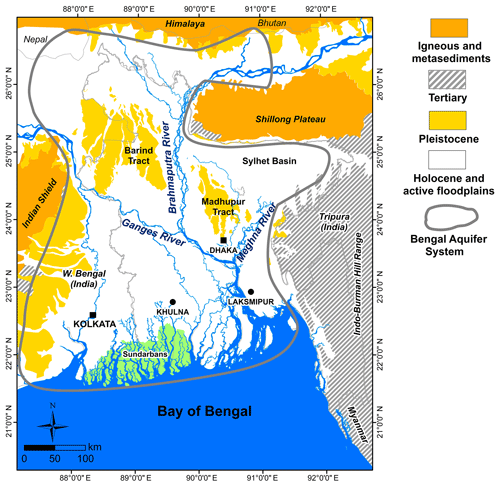
Figure 1 Location map showing the extent of the Bengal Aquifer System (BAS) and the Ganges–Brahmaputra–Meghna (GBM) floodplains.

The generally coupled poro-mechanical nature of geologic-fluid systems is well-established (Neuzil, 2003); porewater pressures affect the stress state and vice versa. These interactions are accepted as important where groundwater conditions are related to faulting (Roeloffs, 1988; Rojstaczer and Agnew, 1989; Sutherland et al., 2017), earthquakes (Manga et al., 2012), pumping-induced aquitard responses (Verruijt, 1969), ground subsidence (Burbey et al., 2006; Erban et al., 2014), glacial loading effects (Bense and Person, 2008; Black and Barker, 2016), and surface water interactions (Acworth et al., 2015; Boutt, 2010). Use of ground surface vertical displacements to infer aquifer or groundwater conditions (Chaussard et al., 2014; Reeves et al., 2014) is also predicated on coupling of the hydraulic and mechanical behaviour of aquifer sediments. For simulation of transient groundwater flow in aquifers, however, a decoupling simplification is frequently applied such that the elastic equation does not need to be solved simultaneously. Thus, the flow equation is solved without consideration of internal stresses and strains or mechanical boundary conditions. Despite this, the poro-mechanical nature of confined aquifers is embedded in the concept of specific storage which incorporates the elastic compressibility of the aquifer materials (Domenico and Schwartz, 1998; Green and Wang, 1990; Narasimhan, 2006). Furthermore, it is associated with the well-known concept of barometric efficiency (Spane, 2002), which describes the response of groundwater pressure to variations in atmospheric pressure, perhaps the example of surface loading effects most familiar to hydrogeologists. The decoupling assumption is reasonable where the effects of mechanical loading can be considered insignificant, either when the changes in load are small or when the applied load is mostly borne by the solid rather than the fluid (Black and Barker, 2016). Neither of these conditions apply to the BAS sediments, which are highly compressible (Steckler et al., 2010) and subject to substantial and extensive TWS mechanical loads due to heavy rainfall, deep flooding, and large river discharges as a consequence of the annual monsoon (Shamsudduha et al., 2012).

In the event of laterally extensive changes to mechanical loads and/or hydraulic heads above the surface of an aquifer, and laterally homogeneous aquifer properties, by symmetry it may be deduced that lateral strains are zero. This condition gives rise to a partial coupling of the elastic and fluid pressure equations (Neuzil, 2003). In the case of partial coupling, changes to the mechanical load due to the changing mass of water near or at the surface may be included within the flow equation, one-dimensionally in the vertical direction, and the solutions will satisfy all the equilibrium and compatibility requirements for stress and strain. There is no need to solve the elastic equation in order to calculate pressures in the aquifer, although once the flow equation is solved, the pressures can be substituted into the elastic equation to provide stresses and strains (Anochikwa et al., 2012). A sub-set of this partially coupled condition occurs where there is negligible groundwater flow, due to very low hydraulic gradients, low permeability, or a combination of both. This can be the situation in extensive fluvio-deltaic aquifers of low topographic relief such as the BAS (Burgess et al., 2017) if mechanical loading is imposed at the surface in a manner which does not induce significant vertical hydraulic gradients. Under these conditions, porewater pressures are determined by changes to surface mechanical loading alone, and changes in groundwater head may be taken as a measure of changes in TWS mechanical loading above the surface of the aquifer. This is the conceptual basis for geological weighing lysimetry (van der Kamp and Schmidt, 1997, 2017; Bardsley and Campbell, 1994, 2007) as used in diverse environments to determine ΔTWS at the scale of individual catchments (Marin et al., 2010; Lambert et al., 2013; Barr et al., 2000; Smith et al., 2017). Geological weighing lysimetry has been suggested as suitable for mapping the variability of ΔTWS within the Bengal Basin (Burgess et al., 2017; Bardsley and Campbell, 2000), complementary to basin-scale estimates based on the Gravity and Climate Recovery Experiment (GRACE) satellite mission (Tapley et al., 2004; Tiwari et al., 2009; Shamsudduha et al., 2012).

The purpose of this paper is to explore the behaviour of the BAS as a poroelastic aquifer subject to a variety of extensive TWS mechanical and hydraulic loads. Poro-elastic theory is very well-established, but has not previously been applied in the context of a thick and extensive aquifer such as the BAS to show the implications for groundwater pressures together with solid strains and ground surface displacements.

The Bengal Basin has a tropical climate dominated by the Indian monsoon, with annual rainfall increasing from 1500 mm in the south and west to 5500 mm in north-eastern Bangladesh, of which 85 % falls during the summer rainy season (May to November) when individual storm events can contribute over 100 mm d⁻¹ (Ravenscroft, 2003). During the monsoon season, river levels rise by 2–8 m, leading to widespread flooding (Steckler et al., 2010), with up to 30 % of the land surface routinely being flooded to a depth of up to ca. 1 m. During the Boro rice irrigation season (January to April), groundwater pumping for irrigation throughout rural areas commonly provides standing water across rice paddies to a depth of ca. 0.1 m (Hasanuzzaman, 2003). For the purpose of this paper, we treat the separate components of TWS across the GBM floodplains as inundation (free-standing surface water such as paddy, floods, beels, and ponds), unconfined storage (water in the unsaturated zone and in saturated pores in the intermittently saturated zone of the aquifer), elastic storage (water in the saturated pores in the permanently saturated zone), and rivers (surface water flowing in rivers and drainage channels). Processes that alter the TWS loads include rainfall and evaporation, rising and falling river stage, flooding and drainage of the land surface, varying soil moisture storage, and a fluctuating water table. Groundwater pumping modifies the water balance and induces additional hydro-mechanical responses. These processes differ in their timing, the geometry of the TWS stores they affect, and the relationship between their resultant hydraulic and mechanical expressions. First, we apply the concept of partial coupling to seek characteristic responses of the aquifer to extensive TWS loads originating as (a) surface water inundation, (b) water table fluctuation, and (c) water bodies hydraulically isolated from the aquifer. These loading styles are examined with and without pumping. The results address important questions for the BAS which are likely also relevant to similarly extensive and strategically important fluvio-deltaic aquifer systems elsewhere in southern Asia (Fendorf et al., 2010; Benner et al., 2008; Larsen et al., 2008; Tam et al., 2014; Xu et al., 2011): how can piezometer heads in the poroelastic aquifer be used to indicate recharge, as required for conventional groundwater resources management; under what conditions can piezometer heads be used to measure ΔTWS using geological weighing lysmetry; can ground surface deflections be related to changes in groundwater storage; and what errors may arise if the poroelastic behaviour of the aquifer is ignored? Second, we apply the partial-coupling approach to these questions in the BAS, with reference to multi-level piezometer data from Khulna and Laksmipur in southern Bangladesh (Fig. 1).

2 Methods

We firstly set out the partially coupled 1-D poro-mechanical approach that we use to examine the implications of specific surface (upper boundary) loading scenarios, with aquifer parameters set to represent the BAS underlying the GBM floodplains (Fig. 1). We consider an equivalent homogeneous uniform medium, as well as a layered structure based on lithological sections. The results provide a diagnostic framework which we apply to analysis of loading styles at Khulna and Laksmipur in southern Bangladesh.

2.1 Poro-mechanical equations

We concentrate on the coupling between water flow and the mechanical behaviour of the BAS sediment, assuming isothermal conditions and that the aquifer material behaves in a linear-elastic way. This is likely to be reasonable under repeated mechanical load–unload cycles, provided there is no secular decline in groundwater level sufficient to cause effective stress to exceed the previous loading maximum.

The 3-D flow and mechanical equations are given in the Appendix. In the event of uniform (1-D) areal mechanical loading, and where lateral strains are negligible, the system simplifies to a flow equation coupled to a mechanical equation for 1-D loading:

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{\kappa }\left(\mathrm{\nabla }p+\mathit{\rho }g\mathrm{\nabla }z\right)=S_{\mathrm{s}}{\displaystyle \frac{\partial p}{\partial t}}-S_{\mathrm{s}}\mathit{\xi }{\displaystyle \frac{\partial {\mathit{\sigma }}_{zz}}{\partial t}}-gJ,\end{array}$$

where κ is the hydraulic conductivity (m s⁻¹), ρ is the fluid density (kg m⁻³), p is the pore pressure (Pa), z is the elevation (m), J (kg m⁻³ d⁻¹) is a fluid source term used here to simulate groundwater abstraction by pumping, ξ is the 1-D loading efficiency (given in Appendix Eq. A5), ν is Poisson's ratio (–), and S_s is the 1-D specific storage typically used in groundwater analyses (van der Kamp and Gale, 1983).

The sediment is assumed to sit on a rigid base, with the top surface free to move, so strain can only be vertical. Thus from Eq. (A1), the vertical stress and strains are related by

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathit{\sigma }}_{zz}=K^{\prime }{\mathit{\epsilon }}_{zz}+{\mathit{\alpha }}_{\mathrm{B}}p,\end{array}$$

where $K^{\prime }=\mathrm{3}K\left(\mathrm{1}-\mathit{\nu }\right)/\left(\mathrm{1}+\mathit{\nu }\right)$, α_B is the Biot–Willis coefficient (assumed equal to 1 to simulate incompressible particle grains), and the bulk modulus, K, and shear modulus, G, are related to Young's modulus E by $K=\frac{E}{\mathrm{3}\left(\mathrm{1}-\mathrm{2}\mathit{\nu }\right)}$ and $G=\frac{E}{\mathrm{2}\left(\mathrm{1}+\mathit{\nu }\right)}$. Changes to the total vertical stress, σ_zz (here termed “mechanical loads”), are applied as a boundary condition at the surface, and are transmitted by the solid skeleton to the entire solid at the acoustic velocity. This represents “partial coupling”; if there are negligible internal loads and provided the changes to the surface load are known, then the flow equation (Eq. 1) can be solved without a need to solve the elastic equations. Deformations can be found from Eq. (2), in conjunction with the compatibility relationships.

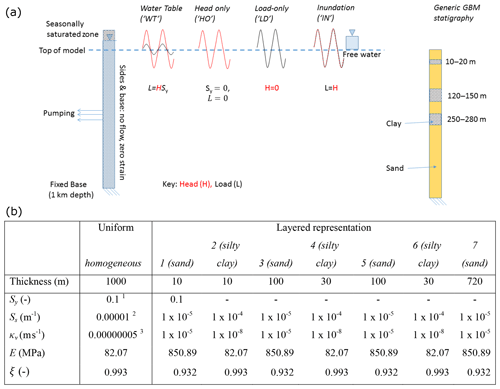
Figure 2 The 1-D model showing (a) the upper surface boundary conditions with head as red lines and mechanical load (weight) as black lines, expressed as metres of water, and a representative stratigraphy for the BAS underlying the GBM floodplains, with the profile depth being 1 km; and (b) parameter values for the uniform and layered 1-D representations. Porosity is taken as 0.1 throughout; ν=0.25; E and ξ are calculated using Eqs. (A3), (A4), and (A5). ¹ Shamsudduha et al. (2011); ² Burgess et al. (2017); ³ Michael and Voss (2009a).

The simplified system considered here is given in Fig. 2. On the upper boundary, the changing TWS is simulated by means of a changing head and a changing mechanical load, according to the nature of the contributing hydrological components. Under this simplification, vertical displacement at the surface will arise in only two ways: by contraction or expansion of the pore space where there is a net change in the volume of water in the column, and by contraction or expansion of the porewater. Being limited to 1-D movement, these volume changes are entirely taken up by vertical displacement.

The reference frame is the base of the model which is assumed fixed in space and set at 1 km depth, acknowledging the variation in aquifer thickness between south-eastern Bangladesh, 3000 m (Michael and Voss, 2009a), and West Bengal, 300 m (Mukherjee et al., 2007). Within this domain, Eqs. (1) and (2) are solved analytically for a homogeneous uniform material in the absence of pumping, and numerically where layers of individually homogeneous materials are simulated, with and without pumping. Where pumping is simulated, the water is assumed to be taken uniformly from the pumping interval. For simplicity, earth tides are neglected.

2.2 Analytical solution

Taking Eq. (1) and assuming homogeneous K and E and that J=0, converting p to metres head, h (i.e. $h=\mathit{\rho }gp+z$), and σ_zz to metres of load (i.e. $L={\mathit{\sigma }}_t/\mathit{\rho }g$ where ρ (kg m⁻³) is the density of water and g (m s⁻²) is the acceleration due to gravity) (Anochikwa et al., 2012; van der Kamp and Schmidt, 1997) gives

$$\begin{array}{}\text{(3)}& {\displaystyle }D{\displaystyle \frac{{\partial }^{\mathrm{2}}h}{\partial z^{\mathrm{2}}}}={\displaystyle \frac{\partial h}{\partial t}}-\mathit{\xi }{\displaystyle \frac{\partial L}{\partial t}},\end{array}$$

where 1-D hydraulic diffusivity is defined as $D=\frac{\mathit{\kappa }}{S_{\mathrm{s}}}$.

We apply the following sinusoidal hydraulic and mechanical loading boundary conditions to Eq. (9), where we introduce a parameter, α, which can be set to zero to give the case of a load in the absence of a varying head, and which otherwise is kept at 1:

$$\begin{array}{ll}\text{(4)}& {\displaystyle }& {\displaystyle }h\left(\mathrm{0},t\right)=H\left(t\right)=\mathit{\alpha }{H}_{\mathrm{0}}\cos \left(\mathit{\omega }t\right),{\displaystyle }& {\displaystyle }L\left(t\right)=S_y{H}_{\mathrm{0}}\cos \left(\mathit{\omega }t\right).\end{array}$$

The following solution is obtained:

$$\begin{array}{}\text{(5)}& {\displaystyle }h\left(z,t\right)=\mathit{\alpha }B\cos \left(\mathit{\omega }t-\mathit{\psi }\right),\end{array}$$

where ψ is the lag (in radians) behind the head H(t) and mechanical loads L(t) at the boundary and

$$\begin{array}{ll}\text{(6)}& {\displaystyle }& {\displaystyle }B=\sqrt{{\mathit{\gamma }}^{\mathrm{2}}+\mathrm{2}\mathit{\gamma }\left(\mathit{\alpha }-\mathit{\gamma }\right)e^{-\mathit{\theta }}\cos \left(\mathit{\theta }\right)+{\left(\mathit{\alpha }-\mathit{\gamma }\right)}^{\mathrm{2}}{e}^{-\mathrm{2}\mathit{\theta }}},{\displaystyle }& {\displaystyle }\mathit{\psi }={\tan }^{-\mathrm{1}}\left({\displaystyle \frac{\left(\mathit{\alpha }-\mathit{\gamma }\right)\sin \left(\mathit{\theta }\right)}{\left(\mathit{\alpha }-\mathit{\gamma }\right)\cos \left(\mathit{\theta }\right)+\mathit{\gamma }{e}^{\mathit{\theta }}}}\right),\\ {\displaystyle }& {\displaystyle }\mathit{\theta }=z\sqrt{{\displaystyle \frac{\mathit{\omega }}{\mathrm{2}D}}}=z\sqrt{{\displaystyle \frac{\mathit{\pi }}{DT}}}\text{ and }\mathit{\gamma }=S_y\mathit{\xi }.\end{array}$$

In the event that the mechanical load, L, is negligible compared to applied head H (e.g. where either S_y is very small or ξ is very small), the hydraulic-only solution is well-known (van der Kamp and Maathuis, 1991):

$$\begin{array}{}\text{(7)}& {\displaystyle }h\left(z,t\right)=H_{\mathrm{0}}\exp \left(-\mathit{\psi }\right)\cos \left(\mathit{\omega }t-\mathit{\psi }\right),\end{array}$$

where the lag is now ψ=θ. Thus, the lag increases with depth or with increasing forcing frequency and the amplitude decreases exponentially with θ.

Displacement and change in groundwater storage can be calculated as the time integral of velocity at the surface. Applying Darcy's law at the surface (z=0) and integrating gives

$$\begin{array}{}\text{(8)}& {\displaystyle }u=\mathrm{\Delta }S=\underset{\mathrm{0}}{\overset{t}{\int }}\mathit{\kappa }{\left.{\displaystyle \frac{\mathrm{d}h}{\mathrm{d}z}}\right|}_{z=\mathrm{0}}\mathrm{d}{t}^{\prime }.\end{array}$$

Equation (8) can be computed by differentiating Eq. (5) with respect to z and then numerically integrating over time. Alternatively, the change in storage can be reported from the numerical model.

2.3 Numerical solution

We used the COMSOL Multiphysics^® software (COMSOL Multiphysics^®, 2018), validated against the analytical solutions for uniform permeability, to solve the stress and flow Eqs. (1) and (2). The finite-element model is unrestricted in terms of spatial distribution of parameter properties and in terms of the boundary condition functions.

2.4 Parameter allocation

Selected parameter values for the BAS underlying the GBM floodplains are given in Fig. 2. The bulk values for the uniform representations are close to the harmonic average of the series components. We next discuss the context in which these parameter selections are made.

2.4.1 Modulus of elasticity, storativity, and loading efficiency

Textbook S_s values (Domenico and Schwartz, 1998) for the materials in the Bengal Basin range between approximately $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ m⁻¹ (dense sandy gravel) and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{2}}$ m⁻¹ (plastic clay). In large-scale modelling of head recession data in the basin Michael and Voss (2009b) achieved their best fits when S_s was $\mathrm{9.4}\times {\mathrm{10}}^{-\mathrm{5}}$ m⁻¹, taking pumped abstraction to be areally uniform. This is the basis for the range in specific storage, S_s, for the BAS (Fig. 2).

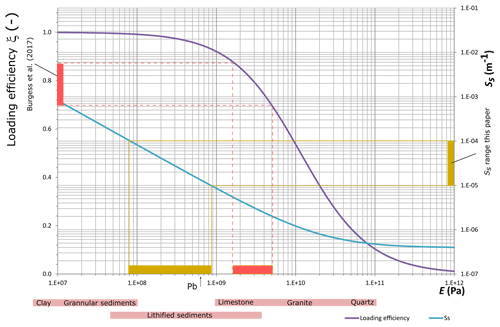
Figure 3 Relationship between 1-D specific storage (S_s), Young's modulus (E), and 1-D loading efficiency (ξ) using Eqs. (A3), (A4), and (A5) assuming a porosity of 0.1 and Poisson's ratio of 0.25. Projections show the corresponding inferred ranges of E based on the S_s range applied ($\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$–$\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$ m⁻¹) and the loading efficiencies calculated via barometric efficiency estimates (0.69–0.87) by Burgess et al. (2017). Pink bars show indicative ranges for common geological materials. Arrow indicates data from 73 m depth at Padma Bridge (Pb) (de Silva et al., 2010).

Specific storage S_s and Young's modulus E are related though Eq. (A3) and to the loading efficiency ξ via Eq. (A4). These inter-relationships are plotted in Fig. 3. It is notable that for E<1 GPa, ξ>0.95 and $S_{\mathrm{s}}>\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ m⁻¹. Thus the loading efficiency only falls significantly below 1 for materials stiffer than around 1 GPa, and where the specific storage is less than $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ m⁻¹. Uncemented sediment is thus expected to have ξ∼1 (Bakker, 2016); on this basis the BAS sediment is unlikely to be sufficiently stiff in the top few hundred metres to allow decoupling of the stress and flow equations. This is corroborated by in situ, high-pressure dilatometer measurements (de Silva et al., 2010) giving E within the broad range for sediments given in Fig. 3.

Estimates of (1-D) loading efficiency based (Jacob, 1940) on barometric efficiency are rather lower: a range of 0.69–0.87 has been determined at Laksmipur in the GBM sediment (Burgess et al., 2017). This is potentially indicative of a considerable stiffening due to burial (E in the range 6–17 GPa), indicating S_s in the range $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{6}}$ to $\mathrm{9}\times {\mathrm{10}}^{-\mathrm{8}}$ m⁻¹. Such a condition might be expected in a Gibson soil (Gibson, 1974; Powrie, 2014). However, the Laksmipur estimates do not decrease systematically with depth, possibly due to changes in stiffness in different materials. The discrepancy may alternatively be related to the timescale of processes responsible for changes in groundwater pressure. Barometric efficiency measurements operationally consider short-term pore pressure changes likely corresponding to the response of relatively stiff aquifer sands, whereas pressure changes in clays are expected to become significant in the longer term. Where short-term moisture loading effects are the key interest (Anochikwa et al., 2012; Bardsley and Campbell, 2000), values for loading efficiency derived from barometric efficiency may be the most appropriate. Here however our main concern is for poro-mechanical consistency and for water load changes operating over a range of timescales; therefore, we adopt S_s estimates based on aquifer pumping tests and use the corresponding ξ and E values (Fig. 3).

2.4.2 Hydraulic conductivity

Basin-scale modelling suggests a horizontal–vertical anisotropy for hydraulic conductivity in the BAS of ∼10 000 (Michael and Voss, 2009b; Ravenscroft et al., 2005). This may be explained as an effective, large-scale value incorporating finer-scale detail of the highly heterogeneous sedimentary record of the past deltaic environment where low-permeability lenses and drapes are laterally discontinuous (Hoque et al., 2017). Michael and Voss (2009a) cite aquifer tests (Hussain and Abdullah, 2001) conducted by the Bangladesh Water Development Board (BWDB) giving a range for hydraulic conductivity (κ) from $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ m s⁻¹. Accounting for anisotropy, κ_v may therefore locally be in the range $\sim \mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$ to $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{7}}$ m s⁻¹. The κ_v values of the uniform and layered representations of the BAS underlying the GBM floodplains (Fig. 2) and of silty clay in layered representations of the Khulna and Laksmipur sites (Sect. 4) lie within this range.

2.4.3 Specific yield

Specific yield is the drainable porosity of the material in which the water table moves. Michael and Voss (2009b) cite a range from 0.02 to 0.19 in Bangladesh, noting that much of the basin has a specific yield in the range of 0.02–0.05. We take S_y=0.1 and 0.01 as order-of-magnitude values typical of sand and clay respectively (Domenico and Schwartz, 1998).

2.5 Upper boundary conditions and groundwater abstraction

Changes to the shallow water budget which have the potential to be laterally extensive and uniform include water arriving as rainfall at the surface and either ponding or moving to the shallow water table as recharge; and water departing the surface or the water table by evaporation, or as runoff to the extensive network of drainage channels. Pumping for domestic and irrigation supply may potentially be considered areally uniform, where sufficiently common and over a wide area (Michael and Voss, 2008). The changing shallow water budget causes a change in mechanical loading to the aquifer system, and if in direct hydraulic continuity with the saturated water column it also causes a change in head. If the shallow water is not hydraulically connected to the saturated aquifer system, the effects of the changing water budget are transmitted to depth by mechanical compression/extension of the sediment, but not by hydraulic diffusion. Changes to the barometric pressure also apply a laterally extensive changing force to the surface of the aquifer and to the water column, and earth tides are also laterally extensive. The daily perturbation on water heads by atmospheric pressure changes is of the order of 0.01 m (Burgess et al., 2017), which is small compared to the annual hydrograph amplitude of the order of 1 m. Barometric pressure and earth tides are both neglected for simplicity here.

To explore the consequences of these hydraulic and mechanical loading sources, the groundwater dynamics associated with three upper surface boundary conditions are modelled here (Fig. 2). Firstly, the effect of a changing level of free water is examined, such as would be seen in paddy fields, ponds, or during floodwater inundation. This condition is here termed “IN”. The change in free-water level is equal to both the change in head and the change in mechanical load at the upper surface (load is here parameterized in metres of water rather than as a stress). Secondly, the effect of changes to unconfined storage due to a moving water table is examined. This condition is here termed “WT”. The change in load is the specific yield times the head. For very small specific yields this condition approaches the hydraulic-only (“HO”) loading case, whereby there is insignificant mechanical load despite the change in head. Thirdly, we examine the effect of a changing surface water store (which could be either free water held above an impermeable barrier, or a perched phreatic aquifer) which is hydraulically isolated from the main aquifer system. A mechanical load only is applied; therefore, no head change is applied to the aquifer, and this condition is termed “LD”.

These three TWS loading scenarios are applied in turn to a uniform and layered representation of the BAS underlying the GBM floodplains. The loading is applied as sinusoidal functions with unit amplitude and a time period of 1 year to simulate the annual hydrological cycle. Additionally, the effects of groundwater abstraction are simulated. Abstraction is taken evenly from the depth interval 50–100 m at an average rate of 0.2 m a⁻¹, either as continuous pumping or as discontinuous pumping π out of phase with the TWS load, as a coarse representation of seasonally varying pumping for irrigation during the dry season.

3 Forward modelling results

The modelled responses of groundwater head to sinusoidal hydraulic and mechanical source terms, together with changes in groundwater storage and ground surface vertical displacements, are illustrated for the GBM environment with uniform properties in Figs. 4 and 5. Figure 4 shows the modelled responses over 10 years at depths of 30, 100, and 300 m, approximating typical BWDB multi-level piezometers (BWDB, 2013). The depth variations of amplitude and phase for groundwater head and the phase lag for surface displacement are summarized in Fig. 5. The effect of layering (Supplement) is to cause departure from the uniform cases, so interpretation of data in a real, heterogeneous aquifer should take into account local deviation from idealized uniform conditions. However, in general, the loading style (“IN”, “WT”, “LD”) and pumping regime are of more significance for the head responses and surface displacements than the detail of the BAS stratigraphy.

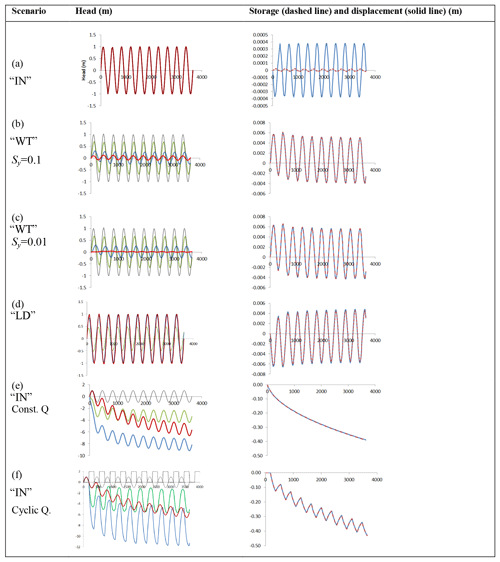
Figure 4 1-D model simulations for the GBM environment, showing results for the scenarios (a) “IN”, (b) “WT” (S_y=0.1), (c) “WT” (S_y=0.01), (d) “LD”, (e) “IN” with constant pumping, and (f) “IN” with cyclic pumping (see text for explanation). The x axis is time in days, shown to 10 years (i.e. 3650 d). The amplitudes reported in the text are calculated from the max–min of the last annual cycle. Left: the y axis is head, in metres (m). The surface head and/or mechanical load boundary conditions (black line) are expressed as equivalent metre head (for the WT condition the unit variation of head is given and the S_y variation in mechanical load is not shown); results are in green (30 m depth), blue (100 m depth), and red (300 m depth) in all cases. For panel (a) results are co-linear at all depths; for panel (f) the intermittent pumping is shown as off/on by the square-wave dotted line. Right: the y axis has dimension of length, in metres (m), showing changes in storage (dashed red line) and surface displacement (solid blue line) for each scenario.

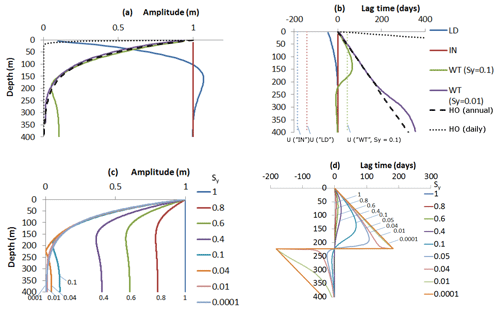
Figure 5 Profiles with depth for (a) amplitude of head response, (b) phase of head response and surface displacement (U), (c) sensitivity of amplitude to S_y for the “WT” boundary condition, and (d) sensitivity of phase to S_y for the “WT” boundary condition. For panels (a) and (b), the colour code for scenarios “LD”, “IN”, “WT” (S_y=0.1), `WT” (S_y=0.01), and HO is shown in panel (b) (see text for explanation); in panel (b), displacement for the WT, S_y=0.01, scenario overlies that for the WT, S_y=0.1 scenario, and so is not shown. (Note: in the instance that ξ is not close to 1, S_y in these plots can be substituted by γ=S_yξ.)

3.1 The free-surface water inundation scenario (“IN”)

Under free-surface water inundation, head changes are characteristically equal in amplitude at all depths and in phase with the inundation signal. Away from the top boundary, the instantaneous head due to loading in this case is h=ξL. Since ξ is close to 1 and H=L, the head is everywhere almost equal to the mechanical load given that at the top boundary the head is also h=H. Therefore, under free-surface water inundation in the absence of pumping, piezometers at all depths can be expected to record the surface water mechanical load, effectively operating as weighing lysimeters. The vertical displacement of the ground surface is extremely small (amplitude ∼0.4 mm), being due to the small compression of porewater itself over the 1 km simulated depth, and is out of phase with the load (i.e. the ground surface moves downwards under an increasing load). The amplitude of change in saturated storage is infinitesimal (∼0.02 mm). The system is essentially “un-drained”: water does not flow into or out of the pores, which therefore experience only minimal strain.

3.2 The variable water table scenario (“WT”)

By contrast with the “IN” scenario, head changes determined by a moving water table are depth-variable in amplitude and phase. When S_y→0 the “WT” condition tends to the head-only end-member (“HO”) and when S_y→1 the “WT” condition tends to the “IN” scenario. The maximum lag for S_y=0.1 is at 137 m depth (or θ=1.94), beyond which it reduces (Fig. 5b). The sensitivity in head to S_y for the “WT” scenario is illustrated in Fig. 5c. The amplitude of head responses is less than the water table fluctuation at all depths. Moreover, only a deep piezometer such as the one indicated at 300 m (Fig. 4b) will behave as a weighing lysimeter in this scenario. Here, heads are in phase with the water table and have approximate magnitude, $h=\mathit{\xi }L=\mathit{\xi }{S}_{y}H$, as in the study by van der Kamp and Maathuis (van der Kamp and Maathuis, 1991) of a thick aquitard overlying a confined aquifer. At 100 m the amplitude of head change is greater than at 300 m and lags behind the water table. At 30 m the amplitude of the head change is greatest and the lag is less than at 100 m. The difference in the head responses compared to the “IN” scenario is due to the difference in magnitudes of the applied head and applied load under the “WT” scenario, causing an instantaneous internal head gradient which subsequently diffuses. Ground surface displacement is ∼4 mm and lags the load by 44 d. With increased head at the top boundary, the upper surface moves upwards because as higher heads penetrate the aquifer the effective stress is reduced. The lag is due to the time taken for the surface head to diffuse downwards.

3.3 The hydraulically disconnected load scenario (“LD”)

Heads in the case of a surface load hydraulically isolated from the aquifer show a third characteristic behaviour. In this case the amplitude of head change increases from zero at the top boundary (Fig. 5a), reaching a peak which is greater than the load, 1.07 at 162 m (or θ=2.29). The amplitude thereafter tends to ξL at greater depth, whilst the lag tends to zero. Therefore heads in relatively deep piezometers potentially represent the surface load under a “LD” boundary condition, as in Fig. 4d, where the heads at 300 m match the surface load, whereas at 30 m they do not. This is due to upward head diffusion towards the surface where the head boundary condition is h=0. The lag which occurs in the “WT” scenario due to the applied head exceeding the mechanical load is reversed in this “LD” scenario, becoming a lead time as the applied load exceeds the applied head. Surface displacement is out of phase with the load, leading by ∼π radians. The ground surface displacement amplitude of ∼4 mm is 10 times greater than for the “IN” scenario, but is still very small in comparison to the annual variability of order 10 cm measured by GPS (Steckler et al., 2010). The “LD” behaviour can be interpreted by means of a decomposition of heads in the manner shown by Anochikwa et al. (2012) (see Supplement).

3.4 The influence of pumping

Introduction of pumping from the depth interval 50–100 m causes hydraulic disequilibrium which continues well beyond the 10 years of simulation, as the head drawdown propagates deep into the profile. As well as drawing water from storage at depth, pumping induces recharge from the surface, there being a downward hydraulic gradient from the surface to the pumped horizon, and upwards from the deeper levels to the pumped horizon. Variable perturbation due to the “IN” surface load is nevertheless clearly evident in the deep groundwater head measurements following correction for secular decline (Fig. 4e). Elastic displacement, manifested as ground surface decline, exceeds 40 cm after 10 years of pumping but, as in the un-pumped “IN” scenario, the annual fluctuation due to surface loading is vanishingly small (0.03 mm). Thus, in addition to the possibility of irreversible plastic deformation, elastic strain may gradually increase due to continuous pumping as stored water is drawn from increasing depths.

Intermittent pumping strongly increases the seasonal variation in heads at the depth of pumping, and this disturbance diffuses to adjacent levels. However, as in the case of continuous pumping, the surface load signal is largely preserved in the deep groundwater head response at 300 m. Also, intermittent pumping induces the same average long-term secular decline in stored water volume and ground surface displacement as continuous pumping, but with additional annual fluctuation caused by the pump switching on and off (decline/drawdown during the dry period when the pumps are used for irrigation and recovery during the rainy season when the pumps are off).

3.5 Model results for ground surface displacement

Taking into account a small correction for the compressibility of water, surface displacement in the model is almost equal to the total change in elastic storage in the permanently saturated aquifer. For the cases where pumping dominates the removal of water, surface displacement is in phase with the pumping (Fig. 4f). For the cases which set up a diffusion of the hydraulic signal between the surface boundary and the aquifer, the phase of surface displacement depends on the hydraulic (non-loading) head changes at all depths (Fig. 4b, c, d). Therefore the lag for vertical displacements under the “LD” surface condition is ∼π out of phase with displacement under the “WT” condition. Note from Eq. (6) that the amplitude and lag are both a function of $\mathit{\theta }=z\sqrt{\frac{\mathit{\omega }}{\mathrm{2}D}}=z\sqrt{\frac{\mathit{\pi }}{DT}}$, and therefore the solutions given here would be scaled in z by any changes to bulk diffusivity, D, and signal frequency (or time period, T): higher frequency would give the same distribution but for a smaller z, and the reverse would be true for diffusivity. Intermittent pumping produces the largest cyclic displacements, however, of the order of centimetres, because this condition causes the greatest volume of seasonal drainage from the formation itself. Where there is non-uniform loading, as produced for example by a variable river stage, lateral groundwater drainage may occur and surface vertical displacements may be greater under these conditions too.

4 Applying the partial-coupling analysis to field data

Applying the 1-D partial-coupling analysis to field data, we examine poro-mechanical perturbations at two sites, Khulna and Laksmipur in southern Bangladesh (Fig. 1). Hourly measurements of groundwater pressure made between April 2013 and June 2014 in three closely spaced piezometers between 60 and 275 m depth at each site are illustrated as hydrographs of equivalent freshwater head in the Supplement. Data on changes of the actual water table at the field sites are unfortunately not available.

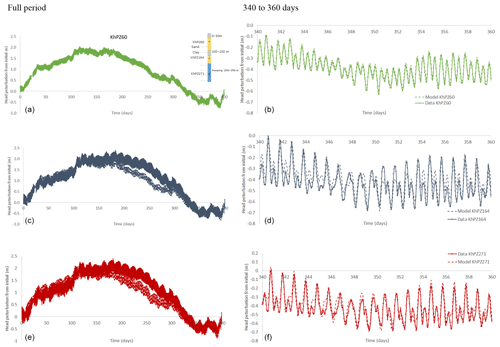
Figure 6 Khulna: comparison of observed heads (solid lines) and simulated heads (dashed lines), starting 27 April 2013, for the WT upper boundary condition (S_y=0.4). The x axis is time in days. The surface loading is set equal to the observed head in KhPZ60, and the surface head is set to the observed head in KhPZ60 divided by S_y. The pumping rate is 2.4 m a⁻¹ for 12 h of each day, switching on at 05:45 (Bangladesh Standard Time). Panels (a, b) are KhPZ60 (green), panels (c, d) are KhPZ164 (blue), and panels (e, f) are KhPZ271 (red).

The objective here is to apply the principles and assumptions of the partially coupled hydro-mechanical approach to reproduce the characteristic features of the multi-level groundwater hydrographs using broadly representative aquifer parameters, rather than to attempt an exact match by inverse modelling. Inspection of the hydrographs at both sites indicates, by reference to Figs. 4 and 5, that mechanical loading significantly influences the measured heads. Additionally, the presence of thick clay aquitards at both sites (Figs. 6, 7) suggests conditions under which heads may be determined solely by mechanical loads and piezometers might behave as geological weighing lysimeters, a possibility which we put to the test.

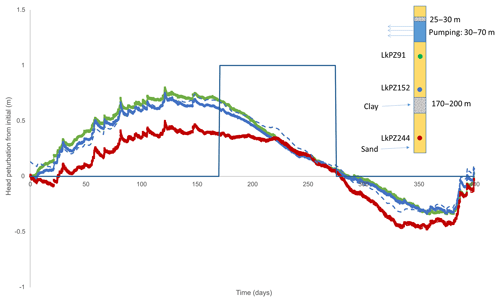
Figure 7 Laksmipur: comparison of observed heads (solid lines) and simulated heads (dashed lines) starting 31 May 2013, for the “WT” upper boundary condition (S_y=0.8), and for LkPZ91 (green), LkPZ152 (blue), and LkPZ244 (red). The x axis is time in days. The surface loading is set equal to the observed head in LkPZ244, and the surface head is set to the observed head in LkPZ244 divided by S_y. The pumping rate is 0.04 m a⁻¹ for the period shown (1 for “on”, 0 for “off”).

The approach at each site is as follows.

• i.

  A two-component sand–clay stratigraphy is based on site data, and parameter values are selected from the ranges described in Sect. 2.

• ii.

  The piezometric readings are compared to examine possible pumping influences which need to be taken into account in the model by means of a simple abstraction pattern. Based on what is known about nearby abstractions an appropriate pumping depth interval is determined. The magnitude of the extraction rate is manually adjusted as a fitting parameter.

• iii.

  Where a piezometer is uninfluenced by pumping, we test its behaviour as a geological weighing lysimeter. The heads in the chosen piezometer are assumed to define the mechanical load at the surface, and this assumption is tested for self-consistency by comparison of the simulations to the data from all three piezometers.

• iv.

  The nature of the upper head boundary is then examined by reference to the implications for a variety of hydraulic loading conditions. For a “WT” boundary, changing S_y manually as a fitting parameter adjusts the magnitude of the applied heads concomitant with the mechanical load.

4.1 Groundwater levels at Khulna, south-western Bangladesh

At Khulna (Burgess et al., 2014), piezometers KhPZ60, KhPZ164, and KhP271 (the numbers indicate depth to the piezometer screen in metres) are located 700 m from the ∼300 m wide tidal Rupsa River, in a grassy compound which also contains municipal water-supply pumping boreholes (Supplement). The lithological sequence (Fig. 6) comprises a surface clay layer overlying sand in which KhPZ60 is screened and a deeper layer of clay at 100 m separating the shallow sand from a deeper sand formation in which KhPZ164 and KhPZ271 are screened. Year-round pumping from 250 to 300 m depth maintains a consistent downward head difference of ∼3 m between the uppermost and the lower two piezometers. It is the transient head variations rather than the absolute steady-state head differences that are of interest here. Bodies of standing water in the vicinity, water in the unsaturated zone, and shallow groundwater combine with the sinuous Rupsa River as sources of TWS load; groundwater pumping is an additional source of hydraulic variation.

The three Khulna hydrographs are characterized by periodic variations containing tidal frequency components throughout the rising and falling limb of the annual cycle, and a series of episodic increments superimposed on the rising limb during the monsoon season; the annual amplitude of groundwater head variation is ∼2.5 m. The amplitude of the tidal frequency components increases between 60 m and 164 to 271 m depth, with no phase lag and with a consistent synchroneity between the piezometer heads and the Rupsa River water level fluctuations, including the semi-diurnal and spring-neap cycles (Fig. 6 and Supplement). Episodic deflections on the hydrograph rising limbs, coincident with rainfall events, are likewise simultaneous at all measurement depths (Burgess et al., 2014). Therefore, by reference to the partial coupling analysis (Figs. 4 and 5), it is evident that heads in the Khulna piezometers respond primarily to mechanical loading by a combination of monsoon water and tidal loading.

At a daily level the time series of groundwater heads in KhPZ164 and KhPZ271 include an additional frequency component which simple analysis of head differences confirms as the hydraulic influence of the daily municipal pumping schedule from which KhPZ60 is protected by an intermediate clay layer. Therefore KhPZ60 alone is taken as recording a solely mechanical loading response and the KhPZ60 head record is applied as the upper boundary condition to represent the varying TWS load at the surface in a 1-D hydro-mechanical model of the Khulna site (Fig. 6), assuming ξ=1. The upper boundary resolves all sources of load acting at the site, including from the Rupsa River, which is a linear rather than an areally extensive load. The ratio of daily (tidal) variability in head at KhPZ60 and in the Rupsa River level is ∼0.06. At an equivalent loading efficiency, the 1.23 m annual variation in river stage would explain ∼0.07 m head variation in KhPZ60, only 3 % of the total. While the response of KhPZ60 to the annual changes of the Rupsa River may be greater than to the tidal changes, depending on the details of aquifer structure and hydraulic connection to the river, 97 % of the annual variation in head at the piezometer is taken here as attributable to changes in TWS other than load transmitted from the river, representing areally extensive loads as required by the 1-D partially coupled analysis. This is likely an over-estimate; measurements of true water table fluctuation and surface flooding depths in the vicinity are necessary to constrain the hydro-mechanical model more closely. Given the relatively well-drained urban context at Khulna and the absence of areally extensive open water that otherwise characterizes the rural areas of the GBM floodplains, a “WT” condition is most likely the dominant loading style, but other sources of loading may also contribute. The layered structure of the Khulna model (Fig. 6) has clay at 0–50 and 100–150 m with sand in between. The daily municipal pumping cycle is implemented as a source term of 2.4 m a⁻¹ for 12 h of each day applied over the interval 200 to 350 m, the rate having been manually adjusted by reference to the daily head fluctuations in KhPZ164 and KhPZ271.

Figure 6 compares the measured groundwater heads with the heads simulated by the model under the assumption of a “WT” boundary with S_y assigned a value of 0.4, with ${\mathit{\kappa }}_{\mathrm{sand}}=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹, ${\mathit{\kappa }}_{\mathrm{clay}}=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{9}}$ m s⁻¹, $S_{\mathrm{s}}={\mathrm{10}}^{-\mathrm{4}}$ m⁻¹ (corresponding to E=82.07 MPa), ν=0.25, and n=0.1. The results are insensitive to S_y being varied in the range from 0.1 to 1 (the latter being equivalent to an “IN” boundary), and are near identical in the case of a “LD” boundary (Supplement). This is because the upper clay effectively isolates the piezometers from the surface hydraulically.

4.2 Groundwater levels at Laksmipur, south-eastern Bangladesh

At Laksmipur (Burgess et al., 2017) the piezometers LkPZ91, LkPZ152, and LkPZ244 are situated in a rural region of rice-paddy and tree plantations on the Lower Meghna floodplain (Supplement), 10 km distant from the River Meghna and 8 km from municipal boreholes which pump from 270 to 300 m depth. Seasonal pumping from depths up to 100 m for rice irrigation is common in the vicinity. The lithological sequence indicates fine sand with occasional silty clay layers. The hydrographs are characterized by a sequence of episodic increments in groundwater head associated with periods of heavy rainfall producing a rising limb of amplitude ∼1 m through the monsoon season; during the dry-season recession, minor periodic fluctuations of order 0.01 m containing atmospheric frequency components become more clearly evident (Burgess et al., 2017). The episodic increments are almost synchronous and of consistent magnitude at all piezometer depths, indicative by reference to Figs. 4 and 5 of groundwater heads responding dominantly to mechanical loading and unloading due to changes in TWS above the aquifer surface.

Here, cyclical head differences between LkPZ244 and the shallower two piezometers indicate hydraulic influences of dry-season pumping on the LkPZ91 and LkPZ152 hydrographs, whereas downward propagation of the hydraulic signals to LkPZ244 is prevented by the clay layer at 170 m depth. Therefore LkPZ244 is taken as recording a solely mechanical loading response and the LkPZ244 head record is applied as the upper boundary condition to represent the varying TWS load at the surface in a 1-D hydro-mechanical model of the Laksmipur site (Fig. 7), with a small offset applied to the initial heads above 170 m depth, consistent with the observed head perturbations being shown as starting from a common zero value. The stratigraphy as modelled draws from the detail of the drillers' log at Laksmipur (Burgess et al., 2017) and the general form of the stratigraphy as seen across the GBM floodplains (Fig. 2). All styles of upper boundary were applied (“IN”, “LD”, and “WT” with a range of S_y values; see the Supplement) in an attempt to distinguish the dominant source of TWS load around the site from the boundary style leading to the best fit with piezometer measurements. In all other respects the models incorporate the dimensions and assumptions as described in Sect. 3, with sand (${\mathit{\kappa }}_{\mathrm{sand}}=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹) and two clay layers (BWDB, 2013) at 25–30 and 170–200 m (${\mathit{\kappa }}_{\mathrm{clay}}=\mathrm{1}\times {\mathrm{10}}^{-\mathrm{8}}$ m s⁻¹), and E=82.07 MPa. A simple dry-season pumping regime over a 105 d period starting 17 November 2013 is implemented as a source term of 0.04 m a⁻¹ applied over the interval 30 to 70 m in the model, manually adjusted by reference to the LkPZ91 and LkPZ152 hydrographs.

For LkPZ244 the simulated heads are an excellent match with measurements over the entire period. The simulated heads for the shallower two piezometers LkPZ91 and LkPZ152 most closely match the measurements under a “WT” boundary with S_y assigned a value of 0.8 (Fig. 7 and the Supplement). The model results therefore confirm that LkPZ244 is isolated from the hydraulic effects of water table variation and of seasonal pumping, and the LkPZ244 groundwater head variation over the observation period is determined solely by mechanical loads at the surface. Therefore LkPZ244 is validated as acting effectively as a geological weighing lysimeter (Burgess et al., 2017).

For the shallower piezometers, the best fit value for S_y is higher than is reasonable for fine sand and more likely indicates the combined effects of a variable water table and fluctuating levels of standing water, in drainage channels, and on paddy fields around the piezometer site, consistent with the field situation. As a consequence of seasonal pumping at 0.04 m a⁻¹, the model shows groundwater is both drawn from storage and induced as recharge from the upper surface, but the amplitude of saturated storage fluctuation is only 6 mm; therefore, changes to the water budget are dominated by recharge to the water table. The surface displacement is predicted at 6 mm amplitude, in phase with the changes in storage.

5 Discussion

5.1 Aquifer responses to discrete modes of terrestrial water variation

Models based on the 1-D partially coupled hydro-mechanical analysis confirm that substantial poroelastic influences should be expected in the Bengal Aquifer System, and that groundwater heads respond characteristically to changes in specific terrestrial water stores (Figs. 4 and 5). Only laterally extensive flooding above an aquifer fully saturated to the ground surface (the “IN” loading style) will drive instantaneous and synchronous head variations at all depths determined by the loading efficiency, inducing negligible flow of groundwater. In any situation involving a variable water table (the “WT” loading style) and for any variable loads hydraulically disconnected from the aquifer (the “LD” style), hydraulic gradients are imposed due to the unequal magnitude of stress and head at the surface. These gradients take time to dissipate, depending on the frequency of the signal fluctuation and the aquifer hydraulic diffusivity, and so lead to differences in amplitude and phase of the head response with depth. In these situations, the relative importance of the hydraulic and mechanical influence is controlled by the aquifer hydraulic diffusivity, the loading efficiency, and the depth of interest. In the case of a fluctuating water table, the difference between the head and stress signals is a function of the specific yield, S_y, in the zone of fluctuation.

The characteristic responses of the aquifer might therefore provide a key to identifying the terrestrial water store dominating ΔTWS, by monitoring vertical profiles of groundwater head. Multiple terrestrial water stores will normally contribute, however, as at Laksmipur and Khulna, so a unique identification may not be possible. This limitation is inherent to the 1-D analysis, which resolves all the contributions to load into one upper boundary condition respectively for head and stress. The analysis indicates how different loads and dynamic responses superpose to produce the observed groundwater hydrographs. In principle, key aspects of the water balance may be better estimated by de-convolving known components of the ΔTWS signal. Anochikwa et al. (2012) assembled field measurements of rainfall and evapotranspiration at a site in Saskatchewan, Canada, using them to define the upper boundary conditions in a 1-D model to examine their hydraulic and mechanical loading separately, before summing the outcomes to simulate the overall hydro-mechanical influence on groundwater pressure. Having determined loading efficiency by reference to barometric effects, they then calibrated their 1-D model against observed groundwater pressures by varying hydraulic conductivity. At Khulna and Laksmipur, measurements of the separate components of the terrestrial water cycle were not available, and hence an indirect demonstration of hydro-mechanical effects was desirable. The simulated and observed heads are in good agreement, consistent with the local conditions, so confirming the 1-D partially coupled analysis as a suitable basis for representing the poroelastic behaviour of the BAS.

5.2 Significance for groundwater monitoring and geological weighing lysimetry

In terms of the extent to which piezometer water levels indicate recharge and drainage, it is only where there is a rapid hydraulic connection between the piezometer and the water table that the piezometer will be sensitive to head change at the water table and therefore to changes in unconfined storage. If a piezometer is hydraulically isolated from surface water and/or the water table and is beyond other transient hydraulic influences, it can respond to changes in the weight of the TWS load, acting as a geological weighing lysimeter (van der Kamp and Maathuis, 1991; Smith et al., 2017). In this case, where the changing load is due to a moving water table, knowledge of the loading efficiency allows the load measurement to be converted into an estimate of recharge and discharge.

In all other situations, a wide range of coupled hydro-mechanical responses can be expected, as we have shown for the BAS (Figs. 4 and 5). Seasonally variable groundwater heads (Fig. 4) are therefore open to misinterpretation as seasonally variable groundwater storage, leading to error in determination of recharge if the poroelastic nature of the response is neglected. Consider heads at 30 m, a common depth for Bangladesh Water Development Board (BWDB) monitoring boreholes (Shamsudduha et al., 2011). For the case of a variable load hydraulically disconnected from the aquifer (Fig. 4d), the annual water level rise is equal to half the amplitude of the load, yet augmentation of elastic storage, by definition in this case, is nil. For the case of variable TWS inundation (Fig. 4a) the annual groundwater level rise is equivalent to the annual depth of inundation, yet augmentation of elastic and unconfined storage is insignificant. Conversely, relative to a variable water table (Fig. 4b, c), groundwater fluctuation at 30 m depth is attenuated. Failure to account for this would lead to an underestimate of recharge to unconfined storage by about 30 %. The error increases as hydraulic diffusivity decreases; therefore, errors could be expected to be greater in the coastal regions of the Bengal Basin, where the thickness of silty clays is greater (Mukherjee et al., 2007). Considerable caution is therefore necessary in the use of even relatively shallow piezometers as indicators of recharge to the water table. A true indication of recharge requires either a shallow tubewell screened over the depth interval of actual water table fluctuation or a deep piezometer responding as a geological weighing lysimeter to the varying mass provided by a fluctuating water table. In the latter case it is recharge to the shallow water table that is measured, not recharge at the depth of the piezometer.

The 1-D hydro-mechanical framework can be applied as a test for the special cases where groundwater head responds solely to mechanical load, and hence to validate the use of geological weighing lysimetry. The laterally extensive loading criterion inherent to the 1-D analysis must apply, and the piezometer screen must be isolated or distant from hydraulic transients originating at the surface or from pumping. We have shown for the BAS that these requirements most likely occur at depths beyond about 250 m, as in the case of “WT” and “LD” loading styles in the absence of pumping (Fig. 5). The inundation (“IN”) style of TWS variation leads to instantaneous transmission of head without loss of amplitude at all depths; in this case piezometers at all depths provide a mechanical record of ΔTWS rather than a hydraulic record of storage variation, and to infer recharge would lead to 100 % error. Our analysis demonstrates a solely mechanical loading response at 244 m depth at Laksmipur, below the level of seasonal irrigation pumping, and at 60 m depth at Khulna, above the level of deep pumping for municipal water supply.

5.3 Significance for ground surface displacements and groundwater storage changes

The models also demonstrate the amplitude and phase of ground surface displacement as a hydro-mechanical consequence of varying terrestrial water stores, and the significance of pumping (Fig. 4e and f). Under simplifications associated with the 1-D model, vertical surface displacements relative to a fixed model base at 1 km depth are approximately equal to the change in elastic storage, the small difference being due to compressibility of water. These changes are minor in the BAS under all TWS loading styles, of the order of millimetres, compared to the displacements in the case of seasonal groundwater pumping, which are of the order of centimetres. Seasonal surface displacements of the order of centimetres have also been attributed to strain acting over a depth scale of hundreds of kilometres due to the load applied by monsoonal inundation over the entire Bengal Basin (Steckler et al., 2010). Strains due to seasonal groundwater pumping at shallow depths may therefore be of the same order of magnitude but out of phase with crustal stain, making ground surface deflections a poor proxy for changing elastic storage in the aquifer. As a corollary, interpretation of seasonal ground surface fluctuations across the GBM floodplains solely in terms of deep crustal deformation (Steckler et al., 2010) potentially requires reassessment in the light of BAS aquifer poroelasticity.

5.4 Limitations and further consequences

In our analysis we have based values for the 1-D loading efficiency, ξ (0.932–0.993), and Young's modulus, E (82–851 MPa), in the BAS on field measurements of S_s, for the sake of internal hydro-mechanical consistency, but we have noted a discrepancy with lower values for the 1-D loading efficiency ξ (0.69–0.87) derived from determinations of barometric efficiency (Burgess et al., 2017). These differences require attention, but the overall conclusions on the significance of poroelastic behaviour in the BAS and the pattern of poroelastic responses characteristic of specific upper surface TWS boundary conditions are unaffected. Although we omitted barometric effects in the generic simulations for the sake of simplicity, it is straightforward to superpose a further loading signal on top of the existing one if required, as for example when deconvolving deep piezometric signals to make water resources assessments (Anochikwa et al., 2012).

Data on changes in the water table would have greatly helped the analysis of loading effects at Khulna and Laksmipur. It is strongly recommended that in future hydro-mechanical analyses of the groundwater dynamics of large layered aquifers such as the BAS, both water table data and deeper head data should be obtained. For the water table, this requires a shallow piezometer to be screened across the full range of fluctuation of the true water table.

Under certain circumstances the extensive load assumption inherent in the 1-D analysis may break down. Rivers, as linear sources of head and load, can be accommodated within the 1-D framework where their contribution to the TWS load is minor as demonstrated at Khulna. In general, however, rivers should be expected to impose laterally variable heads and require a more generalized 2-D or 3-D fully coupled poro-mechanical treatment (Boutt, 2010; Pacheco and Fallico, 2015). An equivalent constraint applies to strains, an additional reason for surface displacement not to offer a secure proxy for groundwater storage in the BAS. The dense distribution of rivers, distributaries, and drainage channels in the Bengal Basin makes the BAS widely vulnerable to loading effects that may not adequately be reduced to a 1-D description; 13 % and 47 % of 1035 piezometers in the BWDB groundwater monitoring network lie within 1 and 5 km respectively of a river.

6 Conclusions

We argue that a 1-D partially coupled approach to hydro-mechanical processes, whereby the loading term is included in the flow equation without the need to simultaneously compute the elastic equation, is a suitable basis for representing the poroelastic behaviour of the Bengal Aquifer System when surface conditions can be treated as areally extensive. Applying a 1-D partially coupled hydro-mechanical analysis, we have shown how the BAS responds characteristically to specific sources of terrestrial water storage variation. Rivers can be incorporated as a component of the 1-D load where their contribution is small, but in general will require a 2-D or fully 3-D treatment.

Groundwater levels, groundwater recharge, vertical groundwater flow, and ground surface elevations are all influenced by the poroelastic behaviour of the BAS. Our results expose the error of the conventional assumption of decoupled hydraulic behaviour which underlies previous assessments of recharge to the BAS. Also, they demonstrate the complexities in applying ground surface displacements as a proxy measure for variations in groundwater storage. We propose that the 1-D partially coupled analysis can be applied to validate when geological weighing lysimetry is applicable in the BAS. In some situations, geological weighing lysimetry offers an alternative approach to recharge assessment.

Appendix A: Poro-mechanical equations

The constitutive isotropic relation between elastic stress and strain, coupled to the pore pressure by Terzaghi's effective stress law, is given by (Neuzil, 2003)

$$\begin{array}{}\text{(A1)}& {\displaystyle }{\mathit{\sigma }}_{ij}=\mathrm{2}G{\mathit{\epsilon }}_{ij}{\mathit{\delta }}_{ij}+\mathrm{2}G{\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathrm{2}\mathit{\nu }}}{\mathit{\epsilon }}_{kk}{\mathit{\delta }}_{ij}+{\mathit{\alpha }}_{\mathrm{B}}p{\mathit{\delta }}_{ij},\end{array}$$

where δ_ij is the Kronecker delta (which is zero when i≠j and one when i=j) and follows the Einstein summation convention; stresses (σ_ij) and strains (ε_ij) are positive in compression; p is the porewater pressure (Pa), ν is Poisson's ratio (–), G is the shear modulus (MPa), and ${\mathit{\alpha }}_{\mathrm{B}}=\mathrm{1}-K/K_{\mathrm{s}}$, where K (MPa) is the bulk modulus of the porous medium and K_s (MPa) is the bulk modulus of the solid grains.

Just as the elastic equations have a pore pressure term, the isothermal, Darcian groundwater flow equation contains a coupled stress term (Neuzil, 2003):

$$\begin{array}{}\text{(A2)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{\kappa }\left(\mathrm{\nabla }p+\mathit{\rho }g\mathrm{\nabla }z\right)=S_{\mathrm{s}\mathrm{3}}{\displaystyle \frac{\partial p}{\partial t}}-S_{\mathrm{s}\mathrm{3}}\mathit{\beta }{\displaystyle \frac{\partial {\mathit{\sigma }}_t}{\partial t}}-gJ,\end{array}$$

where κ is the hydraulic conductivity (m s⁻¹), p is the pore pressure (Pa), z is the elevation (m), J is a source term used here to simulate groundwater abstraction by pumping, and ${\mathit{\sigma }}_t=\left({\mathit{\sigma }}_{xx}+{\mathit{\sigma }}_{yy}+{\mathit{\sigma }}_{zz}\right)/\mathrm{3}$ (Pa).

The 3-D specific storage is defined as

$$\begin{array}{}\text{(A3)}& {\displaystyle }{S}_{\mathrm{s}\mathrm{3}}=\mathit{\rho }g\left[\left({\displaystyle \frac{\mathrm{1}}{K}}-{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{s}}}}\right)+\left({\displaystyle \frac{n}{K_{\mathrm{f}}}}-{\displaystyle \frac{n}{K_{\mathrm{s}}}}\right)\right],\end{array}$$

where n is the porosity and K_f is the modulus of the water (MPa).

The (3-D) loading efficiency, or Skempton's coefficient, β, is defined as

$$\begin{array}{}\text{(A4)}& {\displaystyle }\mathit{\beta }={\displaystyle \frac{\left(\frac{\mathrm{1}}{K}-\frac{\mathrm{1}}{K_{\mathrm{s}}}\right)}{\left(\frac{\mathrm{1}}{K}-\frac{\mathrm{1}}{K_{\mathrm{s}}}\right)+\left(\frac{n}{K_{\mathrm{f}}}-\frac{n}{K_{\mathrm{s}}}\right)}}.\end{array}$$

Where there is areally extensive loading, the 1-D loading efficiency is given by

$$\begin{array}{}\text{(A5)}& {\displaystyle }\mathit{\xi }=\mathit{\beta }\left(\mathrm{1}+\mathit{\nu }\right)/\left[\mathrm{3}\left(\mathrm{1}-\mathit{\nu }\right)-\mathrm{2}{\mathit{\alpha }}_{\mathrm{B}}\mathit{\beta }\left(\mathrm{1}-\mathrm{2}\mathit{\nu }\right)\right].\end{array}$$

The 1-D specific storage is given by

$$\begin{array}{}\text{(A6)}& {\displaystyle }{S}_{\mathrm{s}}=S_{\mathrm{s}\mathrm{3}}\left(\mathrm{1}-\mathit{\lambda }\mathit{\beta }\right),\end{array}$$

where $\mathit{\lambda }=\mathrm{2}{\mathit{\alpha }}_{\mathrm{B}}\left(\mathrm{1}-\mathrm{2}\mathit{\nu }\right)/\mathrm{3}\left(\mathrm{1}-\mathit{\nu }\right)$.

Appendix B: Nomenclature

α	Proportion of mechanical load as head
αB	Biot–Willis coefficient, $\mathrm{1}-K/K_{\mathrm{s}}$
β, C	3-D loading efficiency, Skempton's coefficient,
	or “tidal efficiency”
δij	Kronecker delta
εij	Strain
θ	$z\sqrt{\frac{\mathit{\omega }}{\mathrm{2}D}}=z\sqrt{\frac{\mathit{\pi }}{DT}}$
λ	$\mathrm{2}{\mathit{\alpha }}_{\mathrm{B}}\left(\mathrm{1}-\mathrm{2}\mathit{\nu }\right)/\mathrm{3}\left(\mathrm{1}-\mathit{\nu }\right)$
ν	Poisson's ratio
ξ	1-D loading efficiency
κ	Hydraulic conductivity
ρ	Water density
σij	Stress tensor
σt	Total stress
ψ	Lag (radians)
ω	Angular frequency
a	River half-width
B	Barometric efficiency
E	Young's modulus
D	Hydraulic diffusivity
g	Acceleration due to gravity
G	Shear modulus
h	Head
H(t)	Top boundary head
H0	Amplitude of top boundary head
J	Fluid source term
K	Bulk modulus of porous medium
Kf	Bulk modulus of the water
Ks	Bulk modulus of the solid grains
L(t)	Top boundary load
L0	Amplitude of top boundary load
n	Porosity
p	Pore pressure
Sy	Specific yield
Ss	Specific storage
Ss3	3-D specific storage
t	Time
u	Vertical displacement
x	Perpendicular distance from a river
z	Vertical coordinate