Integrating network topology metrics into studies of catchment-level effects on river characteristics

The spatial arrangement of the river network is a fundamental characteristic of the catchment, acting as a conduit between catchment-level effects and reach morphology and ecology. Yet river network structure is often simplified to reflect an upstream-to-downstream gradient of river characteristics, commonly represented by stream order. The aim of this study is to quantify network topological structure using two network density metrics – one that represents network density over distance and the other over elevation – that can easily be extracted from digital elevation models and so may be applied to any catchment across the globe. These metrics should better account for the multi-dimensional nature of the catchment than stream order and be functionally applicable across geomorphological, hydrological and ecological attributes of the catchment. The functional utility of the metrics is assessed by appropriating monitoring data collected for regulatory compliance to explore patterns of river characteristics in relation to network topology. This method is applied to four comparatively low-energy, anthropogenically modified catchments in the UK using river characteristics derived from England's River Habitat Survey database. The patterns in river characteristics explained by network density metrics are compared to stream order as a standard measure of topology. The results indicate that the network density metrics offer a richer and functionally more relevant description of network topology than stream order, highlighting differences in the density and spatial arrangement of each catchment's internal network structure. Correlations between the network density metrics and river characteristics show that habitat quality score consistently increases with network density in all catchments as hypothesized. For other measures of river character – modification score, flow-type speed and sediment size – there are varying responses in different catchments to the two network density metrics. There are few significant correlations between stream order and the river characteristics, highlighting the limitations of stream order in accounting for network topology. Overall, the results suggest that network density metrics are more powerful measures which conceptually and functionally provide an improved method of accounting for the impacts of network topology on the fluvial system.

1 Introduction

Rivers are integrators of many elements of their catchments (Dovers and Day, 1988). Consequently, integrated catchment management has long been seen as the gold standard for river management and has been adopted in catchments across the globe (Newson, 2009). Research linking patterns of river reach characteristics to catchment-level functioning is currently focussed on characteristics of the terrestrial catchment such as land cover, geology and topography (e.g. Cohen et al., 1998; Harvey et al., 2008; Jusik et al., 2015; Naura et al., 2016; Richards et al., 1996, 1997). Yet “hot-spots” of activity within catchments are identified based on the hydrological connectivity of the catchment (Newson, 2010), a characteristic that is often neglected by catchment-level studies. This missing component of the catchment is critical for true integrated catchment management as the impacts of key management features (e.g. water, channel, land, ecology and human activity) are transmitted throughout the river network (Downs et al., 1991). By investigating the impacts of hydrological connectivity on river form and function, our understanding of catchment functioning can become more holistic and beneficial to catchment management.

Effective catchment management rests not only on improving scientific understanding of river form and function across multiple scales, but also on better integration between the key disciplines of catchment studies: geomorphology, hydrology and ecology. This type of interdisciplinary approach is critical for understanding complex multi-casual relationships in river systems (Dollar et al., 2007). However, catchment connectivity is parameterized differently by different disciplines based on their interests. The discipline of geomorphology focusses on characterizing the morphometry of the catchment, either using general variables which are continuous across the landscape (e.g. elevation, slope, curvature) or specific variables which represent individual features such as catchments (e.g. drainage density, shape, area) or streams (e.g. stream order, stream length) (Evans and Minár, 2011). Hydrology focusses on how the catchment influences hydrograph and flood peak timing and magnitude. Methods such as the Geomorphic Instantaneous Unit Hydrograph (Rodriguez-Iturbe and Valdes, 1979) focus on predicting the travel time of water reaching channels and travelling downstream based the morphology of the catchment, drainage network and precipitation. Aquatic ecology takes a network-centric approach, utilizing dendritic ecological networks (Peterson et al., 2013). This method aims to take a spatially continuous view of rivers (Fausch et al., 2002) in order to appreciate the influence of flow and location in the network on discrete sites chosen for ecological sampling. Spatial statistical stream network models based on the branching of the network (Ver Hoef and Peterson, 2010) are shown to be more accurate than a standard Euclidean distance kriging model, yet only worthwhile if data sites are distributed across the network and are spatially correlated (Peterson et al., 2013). Alternate methods for exploring relationships between network structure and ecological functioning are also based on Euclidean distance along the network (Ver Hoef and Peterson, 2010).

Each discipline represents the elements of the catchment critical to their field, focussing on describing catchment form, catchment flow responses and ecological responses. However, the geomorphology, hydrology and ecology of the catchment are interconnected across spatial and temporal dimensions in the fluvial hydrosystem (Petts and Amoros, 1996). We argue that the overlap between disciplinary methods can be utilized to create a metric to represent the catchment that is meaningful across all disciplines and offers increased potential for effective catchment management utilizing a multi- or inter-disciplinary approach.

This paper repurposes metrics that focus on the topology of the river network for a novel application: to assess the key link between the catchment and reach-level functioning. The metrics represent network density variation within catchments and have functional applications across the fields of geomorphology, hydrology and ecology (Sect. 1.1). The impacts of internal network structure on patterns of river characteristics within catchments are explored by utilizing datasets that are collected for regulatory purposes, with areas of higher network density likely to support greater river quality and diversity (Sect. 1.2). The utility of the topological metrics is compared against stream order, a classic but over-simplified method of accounting for network topology. The topology metrics are calculated for catchments with comparatively low energy and that are influenced by anthropogenic modification as much of the previous evidence for increases in diversity in network-dense areas has been from highly erosive mountainous catchments.

1.1 Quantifying the river network at different scales and dimensions

River network structure, or network topology, is one way to conceptualize the integrated transport of water, sediment and nutrients from the upstream catchment to downstream reaches. The spatial arrangement of links (river channels) and nodes (confluences) concentrates the catchment effect in some areas of the landscape, making network topology a useful archetype of catchment functioning (Gupta and Mesa, 1988).

Drainage density (the total length of the network divided by catchment area) is most commonly used to compare the amount of the catchment covered by river channels, but this fails to quantify spatial variation within catchments, and so offers only a partial means for functionally assessing catchment similarities and differences. To represent within catchment network structure stream order (Strahler, 1957), ordering river links along an upstream-to-downstream gradient based on their upstream connectivity (Fig. 1a) is also commonly used. However, stream order does not account for the spatial arrangement of links, only their relative position in the distance dimension of the catchment. Conceptualizing the catchment in this one dimension leads also to over-simplification; for example, first-order streams are thought of as upland headwater streams, furthest away from the river mouth, yet often first-order streams are tributaries to high-order, lowland streams with different characteristics than upland streams.

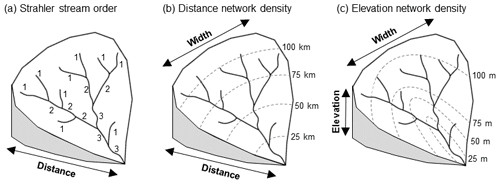
Figure 1 Topological metrics explored in this paper and the dimensions of the network they represent. (a) Strahler stream ordering representing only the distance dimension of the network. (b) Distance network density representing the width dimension of the network at each distance interval (inspired by the network width function; Kirkby, 1976). (c) Elevation network density representing the width dimension of the network at each elevation interval (inspired by the link concentration function; Gupta et al., 1986).

This paper argues that the spatial arrangement of links within catchments must be considered across the distance and height of the catchment to obtain a full three-dimensional appreciation of catchment effect through network topology. Two methods from the field of hydrology – network width function (NWF; Kirkby, 1976) and link concentration function (LCF; Gupta et al., 1986) – offer increased dimensionality by accounting for the width of the network (i.e. the number of links) at successive distances, for the NWF or elevations, for the LCF.

These methods quantify network topology within catchments with functional significance. NWF has hydrological application, representing the travel time of water through the network to predict the timing and magnitude of unit hydrographs and flood peaks (Rodriguez-Iturbe and Valdes, 1979) with a more functionally specific method than the traditional stream-ordering approach (Gupta and Waymire, 1983). Extending applications beyond the field of hydrology, the timing and magnitude of the hydrograph have direct influence on instream ecology, controlling the formation, maintenance and disturbance of physical habitats (Bunn and Arthington, 2002). Longitudinal connectivity of water and sediment through the network is also one of the multiple dimensions of the fluvial hydrosystems approach to catchment ecohydrology (Petts and Amoros, 1996), influencing the capacity for lateral and vertical connectivity and the development of the riparian corridor over time. LCF is less frequently applied in hydrograph prediction than NWF. However, it may better reflect catchment hydrology by incorporating the effect of gradient on the travel time of water, rather than the constant travel time suggested by NWF (Gupta et al., 1986). These metrics also have morphometric significance, reflecting the internal shape of the network by segmenting catchments into intervals to represent how network density changes within catchments (Stepinski and Stepinski, 2005).

This paper repurposes these metrics to reflect network density as a feature of the catchment rather than as a method for hydrograph prediction. Distance network density (modelled on the NWF) (Fig. 1b) and elevation network density (modelled on the LCF) (Fig. 1c) allow for the comparison and quantification of network topological variation both within and between catchment with improved interdisciplinary and functional applicability than the stream-ordering approach.

1.2 Network topology effects on river reach functioning

The topological structure of the river network configures the river ecosystem (Bravard and Gilvear, 1996) by impacting functioning at the reach and sub-reach scales. The distance dimension of the catchment, often represented by stream order (Fig. 1a), reflects upstream-to-downstream gradual changes exhibited by many in-channel features and species. It forms the basis of classic geomorphic models, highlighting the zones of sediment supply in the headwaters, sediment transfer in the mid reaches and sediment storage near the outlet (Schumm, 1977). It is also a key component in classic ecological models such as the River Continuum Concept (Vannote et al., 1980) which describes gradual changes in grain size, channel width, invertebrates, fish species and energy sources along the gradient. Both models suggest that diversity in channel morphology and biota may be highest in the mid reaches as channels transition from erosional to depositional environments. The River Continuum Concept is a popular model, but is critiqued for being too simplistic and for neglecting discontinuity introduced by changes at confluences (Perry and Schaeffer, 1987; Rice et al., 2001). Confluences, as nodes in the network, are associated with changes in hydrological, geomorphological (Best, 1987; Church and Kellerhals, 1978) and ecological (Kiffney et al., 2006; Rice et al., 2001) conditions and have therefore been termed biodiversity “hotspots” (Benda et al., 2004b).

Confluence impacts extend throughout the river network, with increased channel heterogeneity in the tributary and main channel upstream and downstream of the confluence (Rice, 2017). This has led to several theories relating to the impact of numerous confluences in the context of the wider network. The Link Discontinuity Concept shows the impact of confluences throughout the length on the main channel, creating step changes in sediment size before fining continues downstream towards the next confluence along a “sedimentary link” (Rice et al., 2001). The Network Dynamics Hypothesis posits that catchments with higher drainage density, and thus more confluences, will have greater channel heterogeneity (Benda et al., 2004b), despite drainage density failing to be a useful catchment characteristic for predicting local habitat features (Davies et al., 2000). The hypothesis also suggests that catchment shape will influence the impact of confluences, as more compact catchments will have more similarly sized tributaries (Benda et al., 2004b), which have the greatest impact on channel morphology (Benda et al., 2004a), the greatest flow diversity (Schindfessel et al., 2015), and the greatest fish community diversity (Osborne and Wiley, 1992). In contrast, others have found that tributaries that differ most in size have the greatest impact. For example, Jones and Schmidt (2016) suggest that high densities of small tributaries flowing into a large channel cause small, cumulative changes, and Milesi and Melo's (2013) study concluded that small tributaries flowing into large channels in the peripheral regions of the catchment have the greatest impact on macroinvertebrate assemblages.

Interestingly, there is little evidence of anthropogenic impacts at confluences in the literature, but as confluences are proposed concentration points of catchment effects, it seems likely that they may be focal points for anthropogenic impacts. For example, flood events may occur downstream of large confluences as flood peaks converge, creating the need for flood defence measures (Depettris et al., 2000), and scour and erosion at confluence junctions (Best, 1986) increase the need for bed and bank protection. Also, sediment size at confluences is shown to increase in many studies (Church and Kellerhals, 1978; Knighton, 1980), but in tributaries whose watersheds are dominated by agricultural land uses, fine sediments may become dominant at confluences, potentially altering river functioning (Owens et al., 2005).

Many previous studies citing the impact of the network, specifically confluences, on river characteristics were conducted in highly erosive, relatively natural environments (Network Dynamics Hypothesis, Benda et al., 2004b; Link Discontinuity Concept, Rice et al., 2001). Therefore, it will be interesting to assess the impact of network structure on river characteristics in catchments in England, a landscape that has undergone modification impacting catchment functioning for centuries (Macklin and Lewin, 2003).

2 Methods

2.1 Study sites

Four catchments are selected for testing the impact of network topology on river characteristics in England. The catchments are from the Demonstration Test Catchment programme (Fig. 2) which are representative of 80 % of soil and rainfall combinations in the UK (McGonigle et al., 2014). This demonstrates the potential use of topological metrics for catchments with varying geologies and land uses.

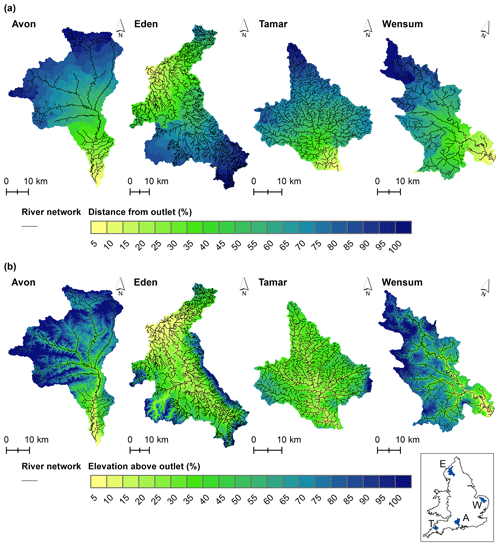
Figure 2 Distance and elevation intervals for each Demonstration Test Catchment: Avon (A), Eden (E), Tamar (T) and Wensum (W). (a) Percentage distance intervals used to calculate distance network density. (b) Percentage elevation intervals used to calculate elevation network density. Map of catchment locations in England in the bottom-right corner.

The Avon and Wensum catchments have similar characteristics, both being dominated by chalk geology with lower average annual rainfall and a high percentage of arable farming land cover. In comparison, the Eden and Tamar are dominated by less permeable bedrock with higher average annual rainfall and a high percentage of grassland land covers. In terms of their morphometry, the Avon and Wensum both have an elongated shape and low drainage density. The Wensum has the lowest relief with a maximum elevation of 95 m. The Tamar has the smallest catchment area (928 km²) and is the most circular. The Eden is the largest catchment (2295 km²) and has the highest maximum elevation (246 m).

2.2 Network topology metrics

Network topology metrics were calculated for each catchment using the 1:50 000 river network map, derived from both a digital terrain model (DTM) and Ordnance Survey data (Moore et al., 1994). Anabranches and incorrectly digitized links in the network are identified using RivEX (Hornby, 2010) and removed. Removing anabranches was necessary as the topological metrics were designed for dendritic networks, so multi-thread channels, either naturally occurring or artificial ditches, would distort the calculations. This resulted in a total of 448, 2812, 1516 and 532 links in the Avon, Eden, Tamar and Wensum, respectively.

Elevation data were extracted from the Integrated Hydrological DTM (Morris and Flavin, 1994), a 50×50 m gridded elevation raster with a 10 cm vertical resolution. Average elevation of each link and the distance from each link to the network outlet were extracted using RivEX (Hornby, 2010).

To extract a measure of network density that varies spatially within the catchment, each network is divided into 20 intervals, each of which represents 5 % of the total distance or highest elevation in the network (Fig. 2). The network is divided in this manner based on the methods of the NWF and LCF, which have functional application to hydrograph prediction. Twenty intervals provide a relatively coarse sampling of the network, compared to the 100 intervals described by Stepinski and Stepinski (2005) when they adapted a morphometric variable, circularity ratio, to represent internal catchment elongation. Here, a total of 20 intervals is chosen so that most intervals contain links for the density calculation whilst ensuring the spatial distribution of network density within the catchment is characterized.

Distance network density was calculated following Eq. (1):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathrm{Distance}\mathrm{network}\mathrm{density}={\displaystyle \frac{\left[n\left(d_{\mathrm{0}}\right),\mathrm{\dots },n\left(d_{\mathrm{i}}\right),\mathrm{\dots },n\left(d_{\mathrm{N}}\right)\right]}{\left(d_{\mathrm{N}}\times \mathrm{0.05}\right)}},\end{array}$$

where the number of links (n( )) within each 5 % distance interval (d_i) from the outlet (d₀) to the maximum distance in the network (d_N) is normalized by the width of the interval (d_N×0.05).

Elevation network density was calculated following Eq. (2):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }\mathrm{Elevation}\mathrm{network}\mathrm{density}={\displaystyle \frac{\left[n\left(z_{\mathrm{0}}\right),\mathrm{\dots },n\left(z_{\mathrm{i}}\right),\mathrm{\dots },n\left(z_{\mathrm{N}}\right)\right]}{\left(z_{\mathrm{N}}\times \mathrm{0.05}\right)}},\end{array}$$

where the number of links (n( )) within each 5 % elevation interval (z_i) from the outlet (z₀) to the maximum height of the network (z_N) is normalized by the width of the interval (z_N×0.05). Normalization allows network densities to be compared between catchments controlling for differences in size and elevation as well as within catchments.

To assess the utility of the multi-dimensional topology metrics in accounting for the spatial structure of the network, the metrics are compared to the one-dimensional Strahler stream-order metric, extracted from the river network dataset using RivEX (Hornby, 2010).

2.3 River characteristics

The impact of network topology on channel functioning is explored using a broad-scale approach, i.e. adapting data collected for regulatory compliance to answer scientific questions. Adapting such datasets to scientific enquiry allows analysis to be conducted in many catchments across a wide spatial extent. There are many habitat monitoring methods across the globe, with 121 survey methods recorded in over 26 different countries (Belletti et al., 2015), so this method may be adapted to other countries.

This study utilizes the River Habitat Survey (RHS; Raven et al., 1996), a regulatory dataset collected by England's Environment Agency, which is used to reflect the river reach characteristics in each catchment. This dataset has been used to identify catchment effects on river characteristics in broad-scale studies by previous research (e.g. Harvey et al., 2008; Naura et al., 2016; Vaughan et al., 2013), but none have included the effects of network topology.

Since 1994, over 24 000 sites have been sampled in catchments across England and Wales, including the Avon (n=418), Eden (n=398), Tamar (n=189) and Wensum (n=315). Surveys were conducted at random sites within each 10 km² of England and Wales to ensure geographic coverage; however, this produces sampling bias as streams in high-density areas will be under-represented in the dataset, which is acknowledged in this study and discussed below.

Table 1 RHS variables calculated from RHS observations.

At each site, over 100 features are recorded along a 500 m reach with 10 “spot-check” surveys conducted every 50 m and a “sweep-up” survey conducted across the whole reach (see Raven et al., 1996, for details). Variables of interest that are hypothesized to be impacted by network structure can be calculated from the RHS observations (Table 1).

The Habitat Quality Assessment (HQA) and Habitat Modification Score (HMS) variables are both amalgamations of RHS observations with individual features given a score derived by expert opinion (see Raven et al., 1998, for more details). The scoring systems are subjective, but HQA and HMS provide overviews of the channel condition that are widely applied for regulatory compliance. The scores are therefore included in this study to reflect how they may be impacted by network topology.

The remaining RHS variables are calculated directly from RHS observations and so are more objective. Sediment size is calculated as a reach average of spot-check observations using the same method as previous studies (Davenport et al., 2004; Emery et al., 2004; Harvey et al., 2008). Flow-type speed was calculated in the same manner as sediment size using values of flow which represent an approximate flow velocity gradient defined in Davenport et al. (2004). These variables were chosen to reflect dominant geomorphic processes occurring in each reach and due to the prominence of sediment size and flow type in defining physical habitats for instream biota (Rowntree and Wadeson, 1996). The variables are likely to be impacted by the density of the river network as they have been shown to be impacted by individual confluences. For example, channels are shown to become more geomorphologically heterogeneous (Benda et al., 2004a) and substrate size has been shown to coarsen at confluences (Rice et al., 2001). Surface flow types are also likely to become more diverse at confluences as the convergence of channels creates a number of different flow environments (Best, 1985) that result in different water-surface topographies (Biron et al., 2002).

It must be noted that the RHS dataset was collected for regulatory compliance and was not directly intended for scientific enquiry. Therefore, there is a limitation in the amount of detail that can be extracted about physical processes as the observations recorded are an average across a 500 m reach. Despite this, the wide spatial coverage of the dataset makes it a powerful tool, allowing analysis to be conducted across multiple catchments with differing characteristics.

For each distance and elevation interval created by the network topology metrics, descriptive statistics (mean, median, 90th and 10th percentiles) of each RHS variable are calculated. Despite the RHS sampling strategy (Jeffers, 1998b) biasing site selection towards less dense areas of the network, most distance and elevation intervals contained RHS sites (with only some low-density intervals not containing RHS sites). This method is designed to account for natural variation and modification at individual RHS sites, in order to assess broad patterns of reach characteristics at the catchment level.

2.4 Statistical analysis

Analysis is conducted with all catchments combined into a single population to identify overall trends across all catchments, a method used in previous broad-scale studies. The analysis is also split into individual catchments to identify how the relationship between network topology metrics and river reach characteristics differed between catchments.

Kendall correlation

Correlation tests are used to determine the strength and direction of the association between the descriptive statistics of the RHS variables and distance network density, elevation network density and stream order to ascertain how reach characteristics respond to network topology. Kendall's correlation method was used as the variables have non-normal distributions, a small sample size and tied data values (Helsel and Hirsch, 2002). The effect size of Kendall's τ is lower than other correlation methods with strong correlations occurring with τ values greater than 0.7 (Helsel and Hirsch, 2002).

As multiple correlations are conducted, false discovery rate (Benjamini and Hochberg, 1995) corrections were applied to the p-values produced from the Kendall correlations to reduce the risk of type I error. The false discovery rate method has been found to be more powerful than other procedures for controlling for multiple tests (Glickman et al., 2014).

3 Results

3.1 Differences in network topology metrics between catchments

The topological metrics developed in this study show the internal structure of the network for each catchment. The separation of the catchments into distance and elevation intervals emphasizes different features of the catchment. The distance intervals (Fig. 2a) are arranged longitudinally within the catchment, highlighting sub-basins within each catchment. The elevation intervals (Fig. 2b) have a radial arrangement, centering around the incised main channel of each catchment.

Distance network density is higher in the Eden (28.4±10.3) and Tamar (44.1±21.9) compared to the Avon (4.7±1.9) and Wensum (6.8±0.7), interesting as the Tamar is the smallest catchment by area. The shape of the distance network density function reflects the internal shape of the network (Fig. 3a). For example, the Tamar has a peaked density distribution reflecting the circular shape of the catchment such that the majority of links are at 55 %–65 % distance from the catchment outlet. The Avon and Eden reflect similar internal network structures, both exhibiting a bimodal density distribution, despite the differences in the number of links in the catchments. The density distribution of the Wensum has a more complex internal distribution of links with multiple peaks in density.

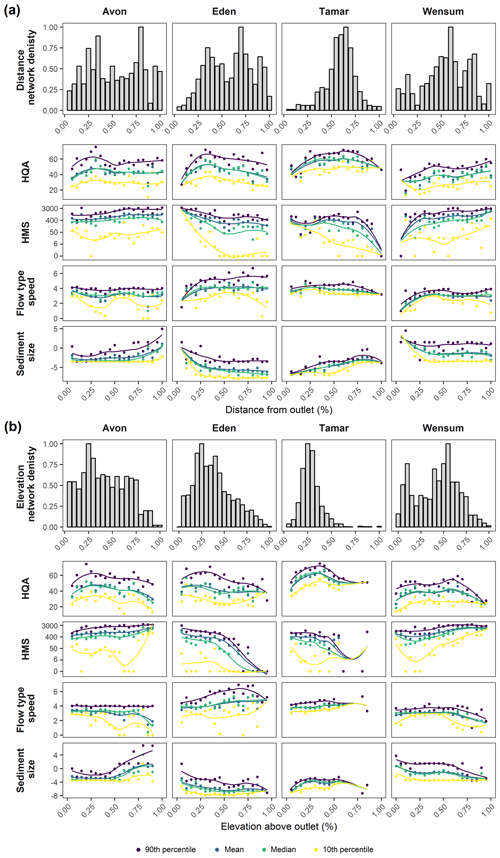
Figure 3 Network topology metrics (a) distance network density and (b) elevation network density. Descriptive statistics of each RHS variable over (a) distance and (b) elevation for each catchment with smooth loess lines to indicate trend. Network topology metrics are normalized between 0 and 1 and HMS score is logarithmically transformed for display purposes.

Elevation network density (Fig. 3b) shows similar density distribution shapes to distance network density, with a unimodal distribution for the Tamar and multi-modal distributions in the other catchments. In contrast to distance network density, elevation network density shows the highest peaks in density in the Tamar (10.3±5.0) and Wensum (10.1±4.3), despite the Wensum having the lowest network elevation, and has lower values in the Avon (3.4±1.0) and Eden (5.8±2.5). The peak densities in the Wensum occur at similar positions in the elevation and distance intervals, whereas the peaks in the other catchments are negatively skewed, showing the network density is highest at low–mid elevations.

Nearly half of the links in each catchment are classified as first-order streams and the number of links declines exponentially towards the highest orders in all four catchments. There are weak correlations ($\mathit{\tau }=-\mathrm{0.03}$ to 0.17) between the three network topology metrics; distance network density, elevation network density and stream order. This suggests that the metrics are independent and reflect different aspects of river network topology.

3.2 River characteristic relationships with network topology metrics

RHS sites in the Avon and Wensum have similar river characteristics. Both have lower habitat quality, high modification, fine sediment and slower flow types than the Eden and Tamar. When all catchments are combined, there are significant (p<0.05 after p-value correction) correlations with most descriptive statistics for each RHS variable and distance network density (Fig. 4). There are consistently positive correlations with HQA and flow-type speed and negative correlations with HMS and sediment size. There are fewer and weaker significant correlations with elevation network density (Fig. 4). The only significant correlations with stream order are with HMS, which shows a negative correlation (Fig. 4).

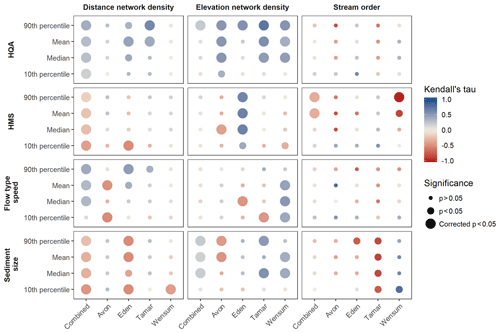
Figure 4 Summary of correlations between distance network density, elevation network density, stream order and RHS variables for all catchments combined and each individual catchment. Significance of correlation is indicated by point size with the largest points significant post p-value correction. Effect size (Kendall's τ) is indicated by colour. No correlation was possible between stream order and 10th percentile sediment size in the Avon due to no variation in the RHS variable.

There are numerous significant correlations between the network topology metrics and RHS variables for individual catchments, many of which were also shown to be significant after the correction to the p-value. The results show that catchments have different responses to the network topology metrics of distance network density and elevation network density. Distance network density only has significant correlations with the regulatory scoring variables (HQA and HMS) in the Eden and Tamar (Fig. 4). Elevation network density, however, has a wider array of significant correlations with the scoring variables, particularly HQA, which shows subtle peaks and troughs reflecting the distribution of both network density metrics (Fig. 3a and b). HMS shows mostly negative correlations, mainly with elevation network density, apart from the Eden, which has significant positive correlation across all HMS descriptive statistics (Fig. 4). Visually, 10th percentile HMS is most variable to network density with peaks and troughs responding to the network density distributions (Fig. 3a and b).

For individual RHS features, the response to network topology varies between catchments (Fig. 4). The Avon has negative correlations between flow-type speed and distance network density, with an evident drop in 10th percentile flow-type speed associated with peaks in network density (Fig. 3a). The Eden and Tamar, however, have positive correlations with mean and 90th percentile flow-type speed for distance network density but negative correlations with median and 10th percentile elevation network density. The Wensum shows positive correlations between flow-type speed and elevation network density. Sediment size has a consistent response to distance network density, with the Eden and Wensum showing negative correlations with the sediment size (Fig. 4). For elevation network density, the Avon shows negative correlations with sediment size, whereas the Tamar and Wensum show positive correlations (Fig. 4).

There were few significant correlations between stream order and the RHS variables in individual catchments (Fig. 4). The only significant correlation after p-value correction is with 90th percentile HMS in the Wensum, which shows a strong negative relationship.

4 Discussion

4.1 A new approach to utilizing network topology in catchment-level analysis

Network density metrics represent an alternative approach to account for network topology in catchment-level studies, optimizing the width dimension of the network (or the number of links in the network) as opposed to the commonplace stream-order metric which only reflects the longitudinal position of links in a network (Fig. 1). This study demonstrates that two topology metrics can be calculated simply from a DTM with GIS and, using a broad-scale analysis of river attributes, can be used to investigate the functional processes within catchments.

While the two network density metrics have similar forms (i.e. forms are consistently unimodal or multi-modal), the spatial configuration of the distance and elevation intervals used in the calculation of network density varies and may impact the effectiveness of each topological metric. Distance network density separates the catchment into intervals based on distance which spread upstream from the outlet (Fig. 2a), reflecting natural sub-basins within the fractal structure of the catchment (Lashermes and Foufoula-Georgiou, 2007). This differs from elevation network density, which separates the catchment into intervals based on elevation which radiate out from the main channel of the network (Fig. 2b). The configuration means that distance intervals contain streams that are in closer proximity to one another rather than the more distal configuration created by the elevation intervals, suggesting a degree of spatial dependency in river functioning. This has been highlighted in previous studies where spatial network structure has a stronger influence on some in-channel processes than predictor variables such as elevation (Steel et al., 2016). However, elevation intervals contain RHS sites that, although they may be distal, may have similar properties as elevation has been strongly related to RHS variables including flow type, substrate, etc., in a number of studies (Jeffers, 1998a; Naura et al., 2016; Vaughan et al., 2013).

4.2 Impacts of network topology on river characteristics

River characteristics are assessed using the RHS dataset. The observations made by the RHS dataset (Table 1) cannot offer the level of detail regarding geomorphological process that river classifications which consider multiple scales can offer (e.g. Brierley and Fryirs, 2000; Gurnell et al., 2016). While process-based classifications are preferable, broad-scale monitoring datasets, such as the River Habitat Survey, may still be useful when combined with map-derived data to explore controls on river characteristics (Harvey et al., 2008; Naura et al., 2016; Vaughan et al., 2013). However, there are biases in RHS data collection, an inherent limitation when using existing datasets (Vaughan and Ormerod, 2010), specifically, the standardized survey length of 500 m reach that will capture differing amounts of natural variability depending on the size of the river. While this must be noted, there are few significant correlations between river characteristics identified with stream order (Fig. 4), which suggests that channel size is not influencing the RHS variables to a great degree in these catchments.

In this study, it is anticipated that sites in high network density areas will have higher levels of habitat diversity, as indicated by previous studies of confluences and networks (Benda et al., 2004a; Best, 1985; Rice, 2017), in turn increasing mean sediment size and flow-type speed compared to sites in low-density areas. The results of the correlations between distance network density and river characteristics when all catchments are combined support this hypothesis, with greater HQA, flow-type speed and coarser sediment sizes observed in areas with high distance network density (Fig. 4).

For individual catchments, elevation network density induces a stronger positive HQA response across all catchments than distance network density (Fig. 4). This supports the evidence that individual confluences (Rice et al., 2006) and high densities of confluences increase physical heterogeneity within the river network (Benda et al., 2004b; Rice, 2017). However, flow-type speed and sediment size respond differently to network density in individual catchments.

Slower flow types are observed in high network density areas of the Avon and Tamar, whereas faster flow types are observed in high-elevation network density areas of the Wensum. Individual confluences are shown to create numerous high- and low-speed flow environments (Best, 1987) that may be observed in surface water topography (Biron et al., 2002). It was expected that the introduction of the additional flow types by a high density of confluences in relatively low-energy rivers would increase mean reach flow-type speed; however, the correlation analysis (Fig. 4) suggests that in some catchments mean flow-type speed is reduced.

Sediment size response also shows variation between catchments. Sediment size is coarser in network-dense areas of the Avon and Eden as expected, but is finer in both the Tamar and Wensum (Fig. 4). The evidence from high-energy rivers shows that sediment becomes coarser downstream and finer upstream of certain confluences (Benda et al., 2004a; Rice, 1998), and in this case high numbers of confluences were expected to increase mean sediment size of the reach. However, the impact on sediment size is dependent on the sediment calibre of the incoming tributary being higher than the main channel, with enough energy to transport the coarse sediment to the confluence for numerous tributaries in an area. The Tamar and Wensum have different ranges of sediment sizes, with the Tamar having coarser sediment than the Wensum on average (Fig. 3). This implies that tributaries in the Tamar may be energy limited, not transporting coarse sediments to confluences, and the Wensum may suffer from inputs of fine sediments from the high percentage of arable land that concentrates in network-dense areas. This has before been observed in a low-energy modified catchment where anthropogenic modifications in tributaries reduced coarse sediment and flow capacity, causing either limited confluence impact or localized sediment fining (Singer, 2008).

Others have related the capacity of confluences to alter reach features to the morphometry of catchments, with larger and more circular catchments containing a higher percentage of confluences that have a significant impact (Rice, 2017). Based on this theory, the Eden and Tamar are likely to have the greatest impact as they are the most circular and steepest of the four catchments (although the Tamar is the smallest by area). Yet there is no clear pattern indicating that these catchments respond differently than the Avon and Wensum (Fig. 4), with catchments responding differently to different variables. This perhaps suggests that rather than network density having a directional impact on factors such as flow-type speed and sediment size, it has an impact on overall heterogeneity at the reach level, as suggested by previous studies, and that specific directional change occurs at the sub-reach level.

An increase in channel modification is also hypothesized due to the increase in flood peak downstream from confluences (Depettris et al., 2000) and the scour and erosion associated with confluence junctions (Best, 1986) potentially increasing the need for bed and bank protection. The correlations between distance network density and HMS when all catchments are combined undermine this hypothesis, showing less channel modification where distance network density is higher (Fig. 4). There were few significant correlations with individual catchments, but HMS in the Eden was consistently observed to be higher in network-dense areas (Fig. 4). This may be due to the Eden's high elevation and steep topography inducing a higher energy environment where scour and erosion processes in areas with high numbers of confluences would be more likely to be present.

Differences in RHS variable responses also differed between the descriptive statistics considered. Often the extremes, 90th and 10th percentiles, showed more significant and stronger correlations than the mean or median (Fig. 4). This may reflect findings from previous studies which suggest that not all confluences cause reach-scale changes (Rice, 1998), that perhaps the changes to river character induced by certain confluences only influence certain reaches, whereas others are left unaffected, creating less pronounced responses in the mean and median of variables. External factors may also influence this trend: for example, 10th percentile HMS visually responds dramatically to network density metrics (Fig. 3a and b) compared to the other descriptive statistics. This suggests that the most natural sites (i.e. with the lowest HMS score) are responding differently to network density, with the most natural sites having less modification in network-dense areas, whereas less natural sites become more modified in network-dense areas. This reflects the HQA score results which visually (Fig. 3a and b) and statistically (Fig. 4) vary with distance network density, except for the 10th percentile. These sites, with the lowest habitat quality and naturalness, are likely influenced by anthropogenic factors that are independent of network density, reducing habitat quality scores at impacted sites.

The two network density metrics have differing impacts on river characteristics. While distance network density shows consistently significant correlations when all catchments are combined, individual catchments respond more frequently and more strongly to elevation network density (Fig. 4). This may be because there is a dramatic split in distance network density values between the more upland, drainage-dense catchments, Eden and Tamar, than the lowland, chalk, low-drainage catchments, Avon and Wensum. The combined correlation will therefore in part reflect the difference between the catchments which have different ranges of river characteristics (Fig. 3). This is not the case for elevation network density, which has higher density values in the Tamar and Wensum than the Avon and Eden, so therefore the characteristics of the catchments will have less bearing on the combined correlation. However, there are patterns identified with distance network density in individual catchments that are not present with elevation network density, increased flow-type speed and sediment size in the Eden and reduced flow-type speed in the Avon with network density (Fig. 4), which show its usefulness.

The results suggest that the distance network density and elevation network density metrics quantify different dimensions of network topology which are shown to exhibit functionally meaningful patterns for river reach characteristics based on the correlation results. Perhaps within catchments elevation network density provides the more powerful metric for individual catchments, but distance network density better accounts for the drainage density of the catchments, allowing it to be applied across multiple catchments.

4.3 Comparison of stream order to network density metrics

The classic method of accounting for network topology, stream order, is critiqued for failing to represent discontinuities in the network and simplifying the network into a gradient. The number of links in different stream orders is consistent across all catchments not reflecting the internal structure of the network or the variety between catchments that is achieved by the distance network density and elevation network density metrics. The analysis of the two network density metrics presented in this paper shows that distances from source and elevation are not mutually exclusive (Fig. 2a and b), contrary to the stream-order metric which represents streams as upstream to downstream or upland to lowland.

Stream order has few significant correlations with many of the river characteristics considered in this study. Negative correlations with HMS in the Wensum were statistically significant post p-value correction, likely driving the significant relationship with all catchments combined for this variable (Fig. 4). This suggests that modification is greater upstream in the Wensum, contrary to ideas that downstream reaches may show greater anthropogenic modification. Intense agricultural land use in the upper reaches of the Wensum is likely to be the cause of the high HMS scores upstream. The lack of significant correlations suggests that stream order and therefore an upstream-to-downstream gradient are not the predominant pattern in river characteristics despite the description of such a gradient by geomorphic (Schumm, 1977) and ecological frameworks (Vannote et al., 1980). This is surprising as distance and elevation, which both reflect the upstream-to-downstream gradient, have proven to be important factors in previous studies explaining patterns of RHS features at a national level (Jeffers, 1998a; Vaughan et al., 2013). This implies that upstream-to-downstream gradient may not sufficiently reflect patterns of river characteristics through the river network within individual catchments. Others have also found that stream order has weak and inconsistent relationships with biodiversity patterns in river systems, arguing that the topological measure has no direct mechanistic control on biodiversity (Vander Vorste et al., 2017). Instead, this study finds that the network density metrics are a more powerful metric which conceptually provide an improved method of accounting for the impacts of network topology on the fluvial system exhibiting relationships with river characteristics, particularly habitat quality score (Fig. 4).

4.4 Applicability of network topology metrics to different environments

Much of the seminal work on network and confluence impacts (e.g. the Network Dynamics Hypothesis, Benda et al., 2004b, and Link Discontinuity Concept, Rice et al., 2001) is conducted in natural, highly erosive catchments with first-hand empirical measurements. However, in an age when rivers and their catchments are increasingly altered by anthropogenic modification (Meybeck, 2003), contemporary studies must not only aim to expand knowledge, but also find methods of transferring knowledge to many, increasingly altered, catchments (Clifford, 2002).

The catchments selected by this study are more greatly modified and, although they reflect a range of fluvial environments in England, are lower-energy catchments than the seminal studies. Benda et al. (2004a) suggest that confluence effects in less active landscapes would be subdued compared to highly erosive landscapes, but the evidence presented here demonstrates the utility of evaluating network topological structure in studies on catchment-level effects in any type of fluvial environment, including those with low-energy and widespread anthropogenic changes. The response of some river characteristics varied between catchments; observations of flow-type speed, sediment size and modifications showed different responses to network density in different catchments. This suggests that the functional effect of these topological metrics is catchment dependent and likely is influenced by external catchment characteristics such as land use not considered in this study, although impact did not appear to vary with catchment topography or circularity, as has been shown in prior studies (Benda et al., 2004a; Rice, 2017). This should be explored further in future research to enable recommendations to be made regarding where and how reaches may respond to network density. The response of habitat quality score was, however, consistent across catchments and between metrics, showing that habitat quality is greater in areas with high network density (Fig. 4), as hypothesized by the Network Dynamics Hypothesis (Benda et al., 2004b) and demonstrated by studies on individual catchments (Rice, 2017; Rice et al., 2006).

The methods presented in this paper are designed to be implemented in any catchment with a dendritic network structure. The topology metrics can easily be calculated from any dendritic network with DTM data using GIS and compared to any site-scale data. This study uses regulatory monitoring datasets so that analysis is targeted to assessment scores and physical features of interest to river managers. Also, the high volume and wide spatial extent of data available from regulatory sources allow for between-catchment comparisons.

5 Conclusions

Although appreciation of catchment-level effects is considered the epitome of understanding river functioning, a key component of the catchment – the river network – is overlooked and oversimplified by catchment-level studies. This study finds that river network density plays a role in structuring the distribution river characteristics throughout the catchment, offering more detailed explanation than the classic stream-order metric. Network-dense areas are generally found to have higher habitat quality and diversity, but modification, flow-type speed and sediment size show different responses in different catchments. This study suggests two potential reasons for this: (1) there is evidence that confluences in the river network increase diversity, as is observed in this study, so the direction of mean river characteristic response may not be consistent, and (2) there may be external factors such as sediment availability, land cover and anthropogenic modification that alter the direction of mean river characteristic response. This paper demonstrates the functional response of river characteristics to network topology and suggests that the inclusion of network topology in catchment-level studies would add a layer of function-based understanding to such studies, linking reaches to their catchments.

The broad-scale methodology adopted by this study allows the network density metrics, which are easily extracted from open-source data using GIS software, to be compared to any regulatory dataset. The use of regulatory datasets allows not only for analysis over a wider spatial extent, but also for more applicable results for regulatory bodies. Therefore, the interdisciplinary approach to characterizing network topology can be applied efficiently and effectively to capture catchment-level impacts on reach-level functioning in any catchment across the globe.