the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modelling of shallow water table dynamics using conceptual and physically based integrated surface-water–groundwater hydrologic models
Mohammad Bizhanimanzar
Robert Leconte
Mathieu Nuth
We present a new conceptual scheme of the interaction between unsaturated and saturated zones of the MOBIDIC (MOdello Bilancio Idrologico DIstributo e Continuo) hydrological model which is applicable to shallow water table conditions. First, MODFLOW was coupled to MOBIDIC as the physically based alternative to the conceptual groundwater component of the MOBIDIC–MODFLOW. Then, assuming a hydrostatic equilibrium moisture profile in the unsaturated zone, a dynamic specific yield that is dependent on the water table level was added to MOBIDIC–MODFLOW, and calculation of the groundwater recharge in MOBIDIC was revisited using a power-type equation based on the infiltration rate, soil moisture deficit, and a calibration parameter linked to the initial water table depth, soil type, and rainfall intensity. Using the water table fluctuation (WTF) method for a homogeneous soil column, the parameter of the proposed groundwater recharge equation was determined for four soil types, i.e. sand, loamy sand, sandy loam, and loam under a pulse of rain with different intensities. The fidelity of the introduced modifications in MOBIDIC–MODFLOW was assessed by comparison of the simulated water tables against those of MIKE SHE, a physically based integrated hydrological modelling system simulating surface and groundwater flow, in two numerical experiments: a two-dimensional case of a hypothetical watershed in a vertical plane (constant slope) under a 1 cm d−1 uniform rainfall rate and a quasi-real three-dimensional watershed under 1 month of a measured daily rainfall hyetograph. The comparative analysis confirmed that the simplified approach can mimic simple and complex groundwater systems with an acceptable level of accuracy. In addition, the computational efficiency of the proposed approach (MIKE SHE took 180 times longer to solve the three-dimensional case than the MOBIDIC–MODFLOW framework) demonstrates its applicability to real catchment case studies.
- Article
(2407 KB) - Full-text XML
- BibTeX
- EndNote
Over the last decades, a number of integrated surface–subsurface hydrologic models have been developed. The main objective of such models is to conceptualise the hydrologic cycle in an integrated way, particularly by coupling the surface and subsurface (unsaturated and saturated zones) hydrological processes. Such integration is particularly important in humid regions where the water table is close to the surface and runoff generation is dominated by variable source area mechanisms (Dunne and Black, 1970; McDonnell and Taylor, 1987). In this runoff generation mechanism, infiltrated water enters the water table, which rises until it reaches the surface, often in valley bottoms, creating areas where any additional precipitation results in saturation excess runoff (McDonnell and Taylor, 1987). Investigation of such a runoff mechanism at the catchment scale can be addressed using physically based models in which the unsaturated zone (UZ) and the saturated zone (SZ) are either explicitly or implicitly coupled. In an explicit coupling approach, a one-dimensional Richards equation for the unsaturated zone is coupled to a three-dimensional saturated flow. In this approach, it is assumed that flow in the unsaturated zone is only vertical and that the groundwater recharge is computed using an iterative water table correction process. MIKE SHE (Refsgaard and Storm, 1995) is an example of one such coupling approach. In the implicit coupling of the unsaturated–saturated zones, the whole subsurface flow process is described using a three-dimensional variably saturated flow equation without an explicit distinction in the interaction between unsaturated and saturated zones (Camporese et al., 2010; Kollet and Maxwell, 2006). This approach more truly reflects the physical processes governing flow but is computationally more expensive when compared with explicit approaches, which themselves require considerable computer resources to solve the unsaturated flow equation at the watershed scale. There is a third group of integrated surface–subsurface hydrologic models, namely externally coupled hydrologic models, where already-existing hydrologic and groundwater models are coupled, such as SWAT–MODFLOW (Chung et al., 2010), TOPNET–MODFLOW (Chenjerayi Guzha and Hardy, 2010), and GSFLOW (Markstrom et al., 2008). MOBIDIC–MODFLOW, the integrated surface–subsurface hydrologic model developed in this study, belongs to that last category of models. Unlike in physically based integrated hydrologic models, the description of the flow in the unsaturated zone in externally coupled models is not based on the Richards equation, and their simplified unsaturated–saturated coupling scheme can restrict their applicability in modelling of shallow water table fluctuations (WTFs).
Seibert et al. (2003) distinguishes three types of interactions between unsaturated and saturated zones based on the water table levels:
-
Type 1. The water table is relatively deep, and there is only one-directional interaction between UZ and SZ. This means that the soil moisture state in the unsaturated soil is independent of the groundwater level and that the role of groundwater in the runoff generation process is not considered.
-
Type 2. The water table is about at the root zone level. The unsaturated soil can get water from the capillary rise in groundwater, so the interaction becomes two-directional, as groundwater recharge can be either positive or negative to create hydrostatic equilibrium with the water table. The unsaturated soil profile is assumed to have a constant vertical extension (unsaturated moisture capacity – the maximum amount of moisture that the unsaturated layer can hold that is constant during the course of simulations). Such assumptions were made by different hydrological models such as TOPMODEL (Beven et al., 1995), SWAT (Neitsch et al., 2011), and MOdello Bilancio Idrologico DIstributo e Continuo (MOBIDIC; Castillo et al., 2015).
-
Type 3. The water table is very close to the surface, and unsaturated moisture capacity can no longer be assumed to be constant as the water table fluctuates. This is the case when the water table rise results in a decrease in the unsaturated soil moisture capacity and a small amount of the infiltration causes a significant rise in the groundwater level (due to the significantly small moisture deficit in the unsaturated zone).
The main problems in modelling of type 3 shallow water tables using externally coupled integrated models lie in (1) the assumption of constant specific yield in the saturated flow module of the integrated model is incompatible with the nonlinear decrease in its value as the water table rises up to the soil surface and (2) the assumption of constant vertical extension for the unsaturated zone does not reflect the inverse relation between the unsaturated and saturated moisture storage discussed in Duffy (2013) and Seibert et al. (2003).
With regard to these limitations, the objective of this study is to propose a series of modifications to the original conceptualisation of the unsaturated and saturated flow process of MOBIDIC in order to extend its applicability for modelling of shallow water table fluctuations while retaining its computational efficiency. To this aim, the conceptual saturated flow scheme of MOBIDIC was replaced with MODFLOW as a physically based three-dimensional groundwater model using the sequential coupling approach (Chenjerayi Guzha and Hardy, 2010). Then, a novel methodology for revisiting the calculation of the groundwater recharge in MOBIDIC, the specific yield in MODFLOW, and the interaction between the unsaturated and saturated zones in MOBIDIC–MODFLOW was developed. The fully coupled surface–subsurface model MIKE SHE is used as a reference for comparison; hence the methodology is based on numerical benchmarking on hypothetical and realistic catchments. Using the WTF method (Healy and Cook, 2002) in MIKE SHE, the rises of a shallow water table were simulated under different sets of rainfall intensity, soil property, and depth to the water table. The simulated responses were then used to reformulate the groundwater recharge of MOBIDIC based on the assumption of a quasi-steady pressure profile in the unsaturated zone as the water table fluctuates. The accuracy of the proposed modifications was first evaluated in a two-dimensional case (constant slope), where the simulated water table rises of the two models under a uniform rainfall rate were compared. In a second experiment, the approach was tested at the catchment scale and under unsteady rainfall conditions. Comparison of the simulated water table responses of the MOBIDIC–MODFLOW against those of MIKE SHE allowed us to evaluate how the unsaturated–saturated interaction scheme of the externally coupled models can be adapted for applications in shallow water table regions.
The water table fluctuation (WTF) method is a simplified approach for the determination of groundwater recharge of an unconfined aquifer based on groundwater level fluctuations. This method is based on the assumption that the rise in groundwater levels is due to the groundwater recharge (Healy and Cook, 2002). Considering the groundwater budget for a representative element (Fig. 1), any change in the water table level (groundwater storage) would be due to a combination of recharge to groundwater (R), inflow from the upstream cell (Qu), outflow to the downstream cell (Qd), and evapotranspiration from groundwater (ETGW) as follows:
where ΔSGW (L T−1) is the change in groundwater storage. Evapotranspiration from groundwater is taken as the direct root water uptake from the saturated zone. Unlike in deep water table conditions, groundwater evapotranspiration in shallow water table regions can be much greater than evapotranspiration from the unsaturated zone (Shah et al., 2007).
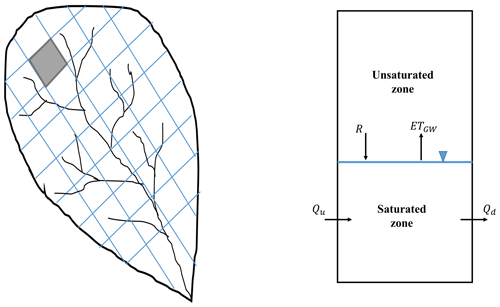
Figure 1Schematic view of computational grids in a catchment and corresponding input and output fluxes over the saturated zone.
Assuming that the water table rise is solely due to the recharge of groundwater requires the sum of other fluxes in Eq. (1) to be zero. This means that the determination of the groundwater recharge using WTF is best applicable over short periods (hours to days) after the onset of rainfall (before any significant redistribution of groundwater recharge to the other fluxes; Healy and Cook, 2002). Therefore,
where Sy (–) is the specific yield and is the change in the water table over Δt. Application of the WTF method requires an estimation of the specific yield which is defined as the volume of drained water per unit of the drop in the water table and aquifer area (Nachabe, 2002):
where Vw (L3) is the volume of drained water, A (L2) is the area of the aquifer, and Δh (L) is the change in the water table level. The specific yield is also defined as the difference between water contents at saturation θsat and at field capacity θfld (the moisture level below which water cannot be drained by gravity; Nachabe, 2002). Such a constant value for the specific yield, however, holds only for deep water tables where changes of the soil moisture profile in the unsaturated zone due to the water table drop are relatively small and the volume of drained water can be approximated as (Fig. 2a). In shallow water tables, however, the specific yield is small (in Fig. 2b, the shaded area is smaller than and approaches zero when the capillary fringe zone extends up to the soil surface; Nachabe, 2002).
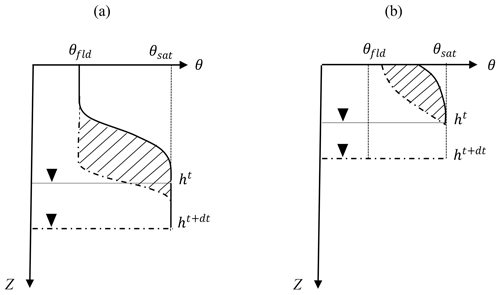
Figure 2Hypothetical soil moisture profile for (a) deep and (b) shallow water tables. The solid and dashed lines are the corresponding profiles before and after water table drops, respectively. The shaded area is the drained water due to a drop in the water table. Modified after Healy and Cook (2002).
3.1 MIKE SHE
MIKE SHE is one of the widely used physically based integrated surface–subsurface hydrological models for a wide range of spatio-temporal applications, ranging from detailed theoretical (single soil column) to operational watershed-scale studies (Graham and Butts, 2005). It has a modular structure for computation of the hydrological processes with different levels of complexity, which is advantageous, particularly in large-scale watershed studies (Kollet et al., 2017). A detailed description of the computation of the hydrological processes in MIKE SHE can be found in Storm (1991) and DHI (2014). We present only the computation of flow in the unsaturated and saturated zones and their coupling approach.
3.1.1 Unsaturated flow
The unsaturated flow is described using the one-dimensional Richards equation as follows (Downer and Ogden, 2004):
where θ (–) is the volumetric water content, k(θ) (L T−1) is the unsaturated hydraulic conductivity, ψ (L) is the pressure head in unsaturated soil, z (L) is the elevation in the vertical direction, and S (T−1) is a sink term (e.g. root extraction). The numerical solution of the Richards equation is based on the implicit finite-difference method in which the soil layer is discretised into the computational nodes and the discretised equation is solved with prescribed upper (rainfall rate or ponded water) and lower (water table level) boundary conditions (DHI, 2014). The main challenge with solving the Richards equation is the computational burden, as it requires fine discretisations in terms of space and time (time steps of seconds to minutes). This can be problematic, particularly in long-term watershed-scale studies.
3.1.2 Saturated flow
Saturated flow in MIKE SHE is computed using the three-dimensional saturated flow equation as the following:
where Kx, Ky, and Kz (L T−1) are the saturated hydraulic conductivity along the x,y, and z axes, respectively; h (L) is the groundwater head; Q (T−1) is the source–sink term; and S is the storativity coefficient (–). The storativity coefficient is either the specific yield, Sy, for unconfined aquifers or the specific storage, Ss, for confined ones (DHI, 2014). Equation (5) is solved numerically over computational grid squares using the finite-difference method with the preconditioned conjugate gradient (PCG) solver, which is also included in MODFLOW (DHI, 2014).
3.1.3 Unsaturated–saturated zone coupling
The explicit coupling approach implemented in MIKE SHE has the advantage of employing different times steps for each zone (seconds to minutes for UZ and hours to days for SZ), which makes the system computationally less expensive compared with the implicit coupling approach (DHI, 2014). However, employing different time steps for the UZ and SZ may result in the generation of mass balance errors in calculating the water flux between the two zones due to (1) an incorrect value of Sy (recommended value is θsat−θfld) in computing the saturated flow and (2) a fixed water table level while the UZ progresses to the next time step (Storm, 1991). The coupling between UZ and SZ follows an iterative process by which the water table is adjusted until the accumulated mass balance error for the entire soil layer (UZ+SZ) falls below a prescribed threshold. The process also calls for adjusting the soil moisture profile. The groundwater recharge is calculated once the iterative process has converged. It should be noted that Sy is considered to be constant in the computational process. The algorithm of iterative adjustments of the water table can be summarised as follows (Storm, 1991):
-
Step 1. At the beginning of the UZ time step, the accumulated mass balance error for the entire soil layer (UZ+SZ) of a soil column (Ecum) is calculated.
-
Step 2. if the accumulated error falls below the acceptable level, the water table does not require any adjustments, and groundwater recharge is calculated as follows:
where R is groundwater recharge and ∑qu is the net inflow to the unsaturated soil. The calculated recharge is applied as the upper boundary condition of the SZ module, and the simulation advances to the next time step.
-
Step 3. if the calculated error is beyond the acceptable threshold, then the water table adjustment is required. Depending on the sign of Ecum the water table will be either raised or lowered, i.e. two steps are followed: (1) if Ecum<0, it means that less water is stored in the profile and therefore the water table has to be raised, using the updated moisture profile in UZ (only the last three nodes of the UZ profile – above the water table – are updated), go to step 1 and repeat; and (2) if Ecum>0, it means more water is stored in the profile and therefore the water table is lowered, and using the updated moisture profile in UZ (same as described above, only for the three lowest nodes of the UZ profile), go to step 1 and repeat.
The iterative water table adjustment continues until the calculated Ecum falls below the acceptable limit. Then the new groundwater recharge is calculated as follows:
where h∗ and h are the water table after and prior to the adjustments, respectively. The calculated groundwater recharge will then be applied as the upper boundary condition of the SZ module, and the simulation advances to the next time step.
3.2 MOBIDIC
MOBIDIC (Castelli et al., 2009) is a distributed continuous hydrologic model in which the components of the hydrologic system are conceptualised as a system of interconnected reservoirs. Such a conceptual formulation of the model makes it computationally more efficient, especially in large-scale watershed modelling (Castillo et al., 2015). The detailed description of the model is available in Castelli et al. (2009) and Castillo et al. (2015).
3.2.1 Unsaturated flow
In MOBIDIC, the unsaturated zone is described by two interconnected reservoirs, i.e. the gravity and capillary reservoirs, to account for corresponding gravity and capillary forces in the unsaturated soil. The water content at field capacity (θfld) is the threshold below which moisture is entirely held in the capillary reservoir. The gravity reservoir interacts with the saturated zone via percolation to the groundwater, and it may also redistribute the additional moisture to the downstream cells (lateral flow in the unsaturated zone; Castillo et al., 2015). The capillary reservoir serves moisture to the plant roots (or evaporation if there is no plant in the computational grid) and can also take moisture from lower groundwater via the capillary rise (Castillo et al., 2015). The moisture capacities of the gravity reservoir and the capillary reservoir, (L) and (L), are defined as (Castillo et al., 2015)
where d (L) is the unsaturated soil thickness and θsat (–), θfld (–), and θres (–) are the water content at saturation, field capacity, and residual, respectively, which are determined based on soil texture classification (Rawls et al., 1982). At each time step, water available for infiltration (net precipitation plus the ponded water on the soil surface) is determined. The infiltration rate takes the minimum value among the saturated hydraulic conductivity, the allowable moisture capacity in the gravity reservoir, and the available water. The infiltration rate, however, might be underestimated for low permeable soils in dry conditions when the capillary force at the soil surface is not negligible (Castelli, 1996). The gravity reservoir is replenished by the infiltrated water. Absorption flux (moisture that is extracted by from the gravity reservoir to the capillary reservoir) is calculated as the following (Castillo et al., 2015):
where κ (T−1) is a linear coefficient that controls the rate of the moisture transfer between the two reservoirs. Finer soils typically have a higher κ value because of low downward moisture gradient. The groundwater recharge (Qper) is calculated as follows (Castillo et al., 2015):
where zw (L) is the depth to the water table, Wg,u (L) is updated moisture in the gravity reservoir, and γ (T−1) is a coefficient that controls the rate of groundwater recharge. The available moisture storage in the gravity reservoir can also contribute to lateral flux to the adjacent cell and is calculated as (Castillo et al., 2015)
where β (T−1) is a coefficient that determines the rate of lateral flow and Wg,u is the updated moisture state in the gravity reservoir after reduction of groundwater recharge. It should be noted that, as the unsaturated flow is strictly vertical in MIKE SHE, we ignored the lateral redistribution of moisture in the gravity reservoir (β=0) to make the structure of the two models consistent.
3.2.2 Saturated flow
Saturated flow in MOBIDIC is described either by a simplified linear reservoir (conceptual scheme) or the Dupuit assumption (Dupuit, 1848). In this study, MODFLOW (Harbaugh et al., 2000) was coupled to MOBIDIC as a physically based three-dimensional finite-difference-based alternative groundwater flow model. MOBIDIC and MODFLOW were coupled using the sequential coupling approach in which the groundwater recharge and water table depth act as the boundary conditions of the coupled MOBIDIC–MODFLOW model (Guzha, 2008). At each daily time step, the water table level determined from the solution of MODFLOW in the previous time step is used in MOBIDIC for the calculation of groundwater recharge (Eq. 12). The calculated groundwater recharge is then applied as the upper boundary condition in MODFLOW, and the water table level of the computation grid is updated. Note that, unlike in MIKE SHE, no fine spatio-temporal discretisation of the system is required in MOBIDIC–MODFLOW, in which a daily time step has been used.
3.2.3 Coupling unsaturated and saturated zones
Unlike MIKE SHE, coupling UZ–SZ in MOBIDIC–MODFLOW is not based on an iterative water table correction procedure. Based on the calculated water table level in the previous time step, the recharge to groundwater can be positive (recharge to groundwater) or negative (extraction from groundwater; Castillo, 2014). The latter occurs when the saturated storage is bigger than moisture storage in the gravity reservoir (Wg). Therefore, the water table in the subsequent time step falls to establish a hydrostatic equilibrium with the moisture level in the gravity reservoir (Castillo, 2014). However, in the former, groundwater is recharged by a higher moisture level in the gravity reservoir. This results in a rise in the water table in the subsequent time step (Castillo, 2014). During the dry periods, the capillary reservoir may also receive water from the capillary rise from the water table, which is calculated as (Castillo et al., 2015)
where dw (L) is the mean distance of the unsaturated layer to the water table, ψ1 (L) is the bubbling pressure, and n (–) is the product of the pore size distribution index (Rawls et al., 1982) and the pore size disconnected index (Brooks and Corey, 1964). The unsaturated soil water pressure (ψ) is a function of the saturation state of the layer and pore size distribution index (m) and is calculated as (Castillo et al., 2015)
It should be noted that the capillary rise is computed where the water table is within the soil profile (zw≤d); otherwise, the capillary rise flux will be zero.
In Table 1, the differences between MIKE SHE and MOBIDIC–MODFLOW with regards to the conceptualisation of the unsaturated flow, saturated flow, UZ–SZ coupling process, and limitations associated with the application in very shallow water tables are summarised. Unlike their disparity in describing the unsaturated zone, the two models share a similar formulation and numerical solution technique for the saturated flow module. The iterative water table adjustments approach in MIKE SHE takes into account the variations in the specific yield as the water table rises and falls. In MOBIDIC–MODFLOW, the specific yield is instead defined as a soil hydraulic parameter and remains unchanged during the course of simulation. This, however, leads to an underestimation of the water table rise as a result of a very small value of the specific yield as the water table approaches the ground surface (Abdul and Gillham, 1989).
We use the WTF method for a soil column to understand how the rise in groundwater is affected by rainfall intensity, soil type, and depth to the water table and how much of the infiltrated rain will percolate to the groundwater. The step-by-step procedure is shown in Fig. 4. Using a soil column with closed boundaries on the sides and bottom, the rise in groundwater level will be only due to the groundwater recharge (see Eqs. 1 and 2). In shallow water table regions, as the water table rises, the specific yield nonlinearly decreases, and, therefore, the actual rise in the water table might be greater than what would be expected by assuming that . This is defined as “reference water table rise” (see Fig. 3) and is calculated as
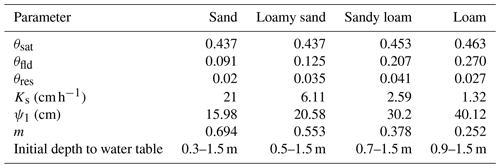
where I (L T−1) is the infiltrated water and Δh (L) is the reference water table rise, which is the expected rise in the water table if the specific yield remains at its ultimate value (θsat−θfld) and the infiltrated water completely reaches the water table. However, depending on the initial water table level and rainfall intensity, it is possible for the water table rise to be smaller than Δh (e.g. for relatively deeper water table and/or low rainfall rate) or that the groundwater recharge takes a value greater than the infiltration rate. The actual water table rise was determined through the coupled unsaturated–saturated flow simulation in MIKE SHE, and knowledge of the ultimate specific yield allowed the calculation of groundwater recharge using Eq. (17). Therefore, by defining (), we can evaluate how the rise of the water table is related to the precipitation rate (assuming no infiltration excess runoff), soil hydraulic property, and depth to the water table. , 1, and mean that the actual rise of the water table is larger than, equal to, or smaller than the reference rise, respectively. Once again, in MIKE SHE, Sy is a constant input of the saturated flow module, and changes regarding its value (decrease in its value when depth to the water table decreases) are captured by the iterative unsaturated–saturated coupling procedure explained in Sect. 3.1.3. The procedure was repeated for four soil types (see Table 2 for the hydraulic properties) and different rainfall intensities (up to the minimum of saturated hydraulic conductivity of the four soils to prevent infiltration excess runoff generation on the soil surface) to further investigate the significance of the rise in the water table of soil types with different characteristics in response to a given pulse of rain. In shallow water tables, loamy soils with a larger capillary fringe range have substantially smaller specific yield values which result in a higher rise of the water table compared with the sandy soils (Abdul and Gillham, 1989). Therefore, its actual rise in the water table is expected to be larger than the reference rise. However, as loamy soils have smaller hydraulic conductivities compared with sand, their water table response will be delayed, especially for deep water tables. To avoid this delayed response, we focussed our analysis on cases where the initial depths to the water table are at a maximum of 1.5 m. Computational time steps were 1 s and 1 min for UZ and SZ, respectively, to avoid numerical instabilities in the simulated water tables by MIKE SHE.

Figure 3Schematic representation of actual and reference water table rise using the WTF method for a soil column subjected to a single pulse of rainfall. In this case the actual water table rise is larger than the reference value, which occurs when the water table is very close to the soil surface.
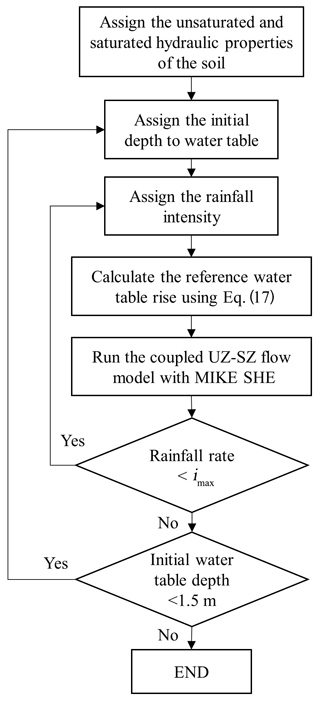
Figure 4Step-by-step procedure of the WTF method used in MIKE SHE. imax is the minimum of saturated hydraulic conductivity of the four soil types. ψ1 is the soil bubbling pressure given in Table 2.
Table 2Hydraulic properties of the soil types used in this study, based on Rawls et al. (1982), and simulated range of initial water table depths.
4.1 Simulation results
Simulation results of the water table rises are shown in Fig. 5. Each dotted curve in the plots is associated with a specific initial depth to the water table (ranging from 0.3 to 1.5 m) and rainfall rate. The plots in Fig. 5 are divided into two zones, i.e. (water table rise exceeds the reference rise, red dots) and (water table rise is less than the reference rise, blue dots). Whereas the lower bound of the chosen initial depth to the water table in Fig. 5 is 1.5 m, the upper bound changes from 0.3 m for sand to 0.9 m for loamy soil. This is due to the differences in water retention characteristics of the soils and the initial moisture deficit in the unsaturated zone. For example, in sandy soil with 30 cm initial depth to the water table (capillary fringe is 15.98 cm), the moisture deficit is 14.98 mm. So, for the infiltration rate bigger than this value, the unsaturated soil becomes completely saturated, and the water table rises up to the soil surface, as can be seen in Fig. 5 (the upper curve ends at a rainfall rate of about 15 mm d−1). The same argument applies to the other soil types. For loamy soil with a capillary fringe value of 40.12 cm, the initial depth to the water table of 90 cm corresponds to the moisture deficit of 23.97 mm in the unsaturated zone. Therefore, the upper curve for loamy soil ends at this depth to the water table and rainfall intensity.
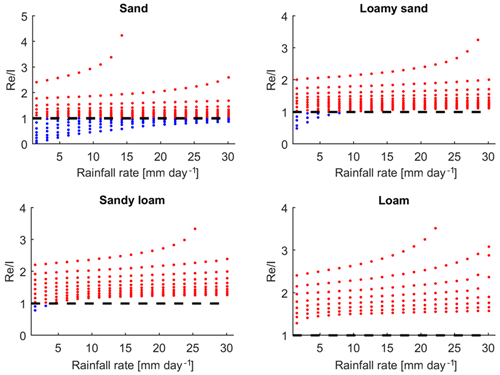
Figure 5Variations of the ratio of recharge to infiltration with rainfall and initial depth to water table in different soil types simulated by MIKE SHE. The red dots are , and the blue dots are .
For a given initial water table level, moving from low to high rainfall intensities results in increasing the ratio of recharge to infiltration, shifting from a situation where (blue dots) to (red dots). Also, while the case where is more common in sandy soils, the opposite is found as soil texture becomes finer (e.g. loamy soil). This means that the actual water table rise in fine-textured soils (loamy sand to loam) is almost always larger than would be expected based on using a constant value for the specific yield (θsat−θfld).
Note that for all soil types analysed, the values show small sensitivity to increases in rainfall intensity as the depth to the water table gets larger, e.g. in sandy soils and loamy soils when the water table is deeper than 50 cm and 1 m, respectively. This can be attributed to the existence of significant initial soil moisture deficits found at larger initial water table depths. On the other hand, as the water table gets closer to the soil surface, an increase in the rainfall rate generates a significant water table rise, yielding a substantial increase in . This demonstrates the importance of the soil moisture deficit (and its ratio to the precipitated rainfall) with regards to the water table rise.
As discussed in Sect. 3, MOBIDIC's unsaturated soil depth (d in Eqs. 7 and 8) remains constant during the course of a simulation (both in rainy and subsequent draining periods). This is due to its conceptualisation of UZ and SZ, as their interaction is not aimed to address the reverse relationship between them in very shallow water table cases. The proposed changes in this paper aim to make the model applicable to such cases. The changes are as follows:
-
It is assumed that the unsaturated soil layer thickness, d, is no longer a constant input of the model and changes with water table fluctuations. Hence, the total moisture capacity of the reservoirs ( and ) is determined similarly to Eqs. (7) and (8), but with replacing d by the depth to the water table (zw). Therefore, the water table rise or fall results in a decrease or increase in moisture capacities of the reservoirs. Such assumption is valid when the groundwater level is treated as a moving boundary and there is a continuous transfer of moisture between the unsaturated and saturated zones.
-
The specific yield in calculation of the groundwater head by MODFLOW is determined based on a soil water retention model (e.g. Brooks and Corey, 1964) and the hydrostatic equilibrium assumption in the unsaturated zone (suction profile in unsaturated zone changes from steady state to another over the changes in water table; Hilberts et al., 2005; Duke, 1972):
where zw is depth to the water table and other variables are as defined above. Validity of the hydrostatic equilibrium assumption is justified in shallow water table regions where redistribution of the infiltrated water is rapid (Bierkens, 1998). Therefore, with any changes in the water table level, the specific yield is adjusted for the calculation of groundwater dynamics in the next time step. This is especially important in shallow water table cases, as the specific yield decreases significantly as the water table rises up to the soil surface.
-
The groundwater recharge R (L T−1) is a function of available moisture in the gravity reservoir, the unsaturated soil moisture deficit, and the infiltration rate and is calculated as follows:
where I (L T−1) is the infiltration rate, and ω (–) is a function of soil type, the infiltration rate, and the water table level, which determines how much water will be transferred to the saturated zone. It should be noted that, similar to the original conceptualisation of the unsaturated flow in MOBIDIC, only the gravity reservoir contributes to the groundwater recharge. The proposed conceptualisation of the interaction between UZ and SZ is shown in Fig. 6. Starting with a hydrostatic equilibrium moisture profile in the UZ, the available moisture in the reservoirs, Wg and Wc, and the moisture deficit in the unsaturated profile are determined. The rise in the water table results in a reduction of the moisture capacities of the reservoirs and , as well as Wg and Wc, and the moisture deficit in the unsaturated profile. When the water table falls, however, there is an increase in these quantities.
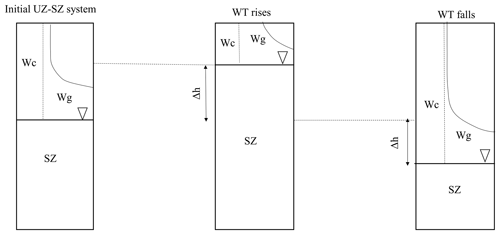
Figure 6Conceptualisation of the interaction between UZ and SZ in MOBIDIC–MODFLOW in rising and falling water table conditions.
5.1 Interpretation of the new groundwater recharge equation in MOBIDIC–MODFLOW
To interpret the proposed groundwater recharge equation (Eqs. 19 and 20), let us first analyse its limit values. As , a decrease in ω results in a decrease in R (and vice versa). The coefficient ω can be either positive or negative. When positive, recharge to the groundwater reservoir is larger than the infiltration rate, and when negative, groundwater recharge is a portion of the infiltration. The specific case for which ω=0 occurs is when R=I. Such flexibility in the value range of ω is important, as it makes the model applicable for cases where adding a small rainfall amount can cause a significant water table rise, which may occur in humid regions. However, its precise determination can be problematic, as it is a complex function of the water table level, soil type, and rainfall (infiltration) intensity. In general, for a known water table level, an increase in the rainfall rate will require larger ω values to match the water table rise of MIKE SHE and MOBIDIC–MODFLOW. Equation (19) was calibrated for ω by using simulated water table rises of MIKE SHE. This allowed investigating how combinations of soil types, rainfall intensities, and water table depths influence the behaviour of groundwater recharge and how this can be captured using the conceptual UZ–SZ formulation as in MOBIDIC–MODFLOW.
5.2 Simulation results
Figure 7 displays the values of parameter ω in Eq. (19) obtained by fitting the water table rises of the MOBIDIC–MODFLOW model to the water table rises simulated by MIKE SHE for the cases presented in Fig. 5. The negative and positive values of ω are shown in red and blue dots, respectively. It can be seen that for a specified water table level, increasing the rainfall rate requires higher values of ω to fit the water table rise of MOBIDIC–MODFLOW than that of MIKE SHE. Furthermore, the relationship is nonlinear. This further shows the complexity of the interactions between the UZ and SZ under shallow water table conditions. Note that in sandy soils, most of the ω values are negative, while the opposite is found for loamy soil. This is because the water table rise for loamy soils is larger than for sandy soils (smaller specific yield and available moisture deficit in the unsaturated profile). Comparing the scatterplots in Fig. 7 reveal that unlike loamy soils, in sandy soils with relatively deeper initial water tables, the changes in ω (with changes in rainfall rate) are quite small. This is related to the initial moisture deficit in the unsaturated profile, as discussed in Sec. 4.1.
These ω values are arranged in a look-up table that can be used to simulate the UZ–SZ interactions in MOBIDIC–MODFLOW in the following way: at each time step, based on the specified water table depth, soil type, and rainfall rate, a value of ω is obtained by interpolation from the look-up tables. The determined ω values are then used for calculation of the groundwater recharge using Eq. (19). The groundwater recharge is then applied as the upper boundary condition to the saturated computation layer. Using the specific yield calculated with Eq. (18), MODFLOW updates the groundwater head and water table level values. The updated levels are then transferred to MOBIDIC–MODFLOW for the determination of moisture storage in the capillary and gravity reservoirs (Wg and Wc). This procedure is repeated for the entire simulation period. The next section compares the performance of the MOBIDIC–MODFLOW model against MIKE SHE in two cases, a hypothetical vertical two-dimensional slope model and a small a pseudo-hypothetical watershed.
The appropriateness of the proposed changes in the conceptualisation of UZ–SZ interactions of MOBIDIC–MODFLOW was tested by comparing its simulated water table results against those of MIKE SHE in two test cases. The description of the test cases follows.
6.1 Two-dimensional case
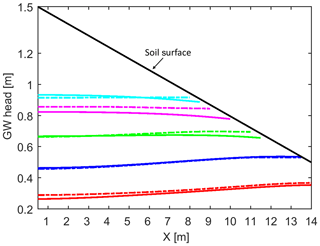
So far, our analysis focussed on a single soil column in which the coefficient of the proposed groundwater recharge, ω (Fig. 7), was determined based on the simulated water table rise by MIKE SHE (Fig. 5). In order to analyse the performance of the proposed approach in cases where there is lateral interaction between saturated computational grids, simulations of the water table rise were performed for a small soil box measuring 14 m long, 1.5 m high, and 1 m wide and filled by sandy soil, identical to the one used in the soil column analysis. The soil box has closed boundary conditions on x=0, x=14 m, and the bottom side, and it is assumed that the initial water table is m. Since the rainfall is continuous during the entire simulation period, configuration of the such boundary conditions results in a higher water table rise in the toe of the slope (shallower water table) and generation of saturation excess runoff starting from downhill moving to the uphill. The hillslope is discretised into 28 columns (Δx=0.5 m), and the vertical discretisation of the unsaturated layer in MIKE SHE is Δz=1 cm. A 10 mm d−1 constant rainfall is applied for 20 d, and the simulated water table rises of the two models are compared.
6.1.1 Simulation results
The simulated water tables of the two models are shown in Fig. 8. It can be seen that the predicted water tables of the two models are very close. The slight mismatch between the predicted water table heads of the two models can be attributed to the fact that in MOBIDIC–MODFLOW, the response of groundwater to the precipitated water is immediate, that is, within the same time step (1 day). This is not the case in MIKE SHE, where the simulation time step is much shorter at 1 s. The saturated length (the length where water table is at the soil surface) predicted by the two models is closely matched, which shows that the simplifications in the UZ–SZ interaction of MOBIDIC–MODFLOW can mimic the complex dynamical interaction between the two zones. Note that the generated saturation excess runoff by two models was removed from the soil surface, as the flow routing module was not included in the simulations.
6.2 Catchment scale
6.2.1 Borden catchment
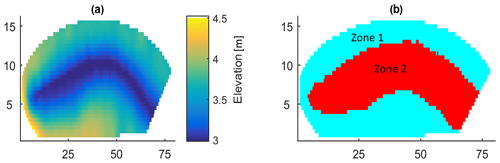
In order to further evaluate the suitability of the proposed conceptualisation of UZ–SZ in MOBIDIC–MODFLOW, the water table fluctuations of the two models at the Borden catchment for the month of May 2015 were compared. The Borden catchment is located approximately 70 km northwest of Toronto, Ontario (Jones et al., 2006). The site is about 20 m wide and 80 m long, and it was subjected to several experimental (Abdul and Gillham, 1989) and numerical rainfall–runoff studies (Jones et al., 2006; Kollet et al., 2017; VanderKwaak, 1999). It is assumed that the catchment consists of a single homogeneous sandy soil identical to the one used in the previous simulations (see Table 2 for hydraulic properties) without any vegetation cover. The motivation for simplifying the watershed physiographic characteristics here was to evaluate the MOBIDIC–MODFLOW in a “real” watershed while emphasising differences in UZ–SZ dynamics simulated by the conceptual approach as compared with a physically based numerical model.
The digital elevation model (DEM) of the Borden catchment has a spatial resolution of 0.5 m, is available at http://www.hpsc-terrsys.de (last access: 7 April 2019), and is shown in Fig. 9a. The initial water table level was assumed to be at 1 m below the catchment's outlet (at elevation 1.98 m). The site has closed boundaries on the sides, and it has a horizontal bedrock at an elevation of 0 m. The measured rainfall at the Borden site for May 2015 used in the numerical experiment (data available from Environment Canada, http://climate.weatheroffice.ec.gc.ca (last access: 7 April 2019) for the Borden AWOS station). The rainfall hyetograph (Fig. 11) consists of 10 events, with a total amount of 77.2 mm and maximum of 24.8 mm at day 25, where a significant rise in the water table is expected. The catchment was subdivided into two zones based on the initial depth to the water table as shown in Fig. 9b. Zone 1 represents the initial depth to the water table less than 1.5 m (red zone in Fig. 9b), and cells in zone 2 have initial depth to the water table larger than 1.5 m (blue zone in Fig. 9b). The calculation of groundwater recharge and interaction between UZ and SZ followed the modifications presented in Sect. 5 (the ω parameter in Eq. 19 was made variable for water table levels less than 1.5 m), and changes in the groundwater head in zone 2 were simulated using the original conceptualisation of MOBIDIC explained in Sect. 3.2. Therefore, these two structures together cover the dynamics of the water table for the whole catchment. Note that, for water table depths greater than 1.5 m, the moisture capacities of the reservoirs (, ) remain constant with a rise or fall of the water table (Sect. 3.2). Such distinction based on depth to the water table was made to limit the extrapolation errors associated with the determination of ω for water table depths larger than 1.5 m. Besides, for these zones, the assumption of an inverse relationship between the unsaturated and saturated moisture storage is questionable, as discussed in the Introduction.
6.2.2 Simulation results
The difference in the simulated water table level of the two models is shown in Fig. 10 for the selected simulation days after the rainy events. The predicted groundwater head of the models at the outlet of the catchment is also compared in Fig. 11. It can be seen that the two models generally compare well.

Figure 10The difference in simulated water tables by MIKE SHE and MOBIDIC–MODFLOW (hMOBIDIC-MODFLOW−hMIKESHE; m) at different time steps.
However, MOBIDIC–MODFLOW slightly predicts a higher water table rise as compared with MIKE SHE following rainfall events (e.g. events on days 11, 18, and 25). At day 6, MOBIDIC–MODFLOW simulates higher water table levels compared with MIKE SHE because of the higher groundwater recharge received by the grid cells in zone 2 and subsequent lateral saturated flow from zone 2 to zone 1. Note that in the original UZ–SZ scheme of MOBIDIC, if the groundwater level is below the modelled soil layer (as in zone 2), the groundwater recharge is a linear function of the moisture content of the gravity reservoir (see Eq. 12). However, in MIKE SHE, the groundwater recharge is calculated from the solution of the Richards equation, considering the water table level to be the lower boundary condition. Therefore, the magnitude of groundwater recharge simulated by MIKE SHE for zone 2 is smaller than MOBIDIC–MODFLOW. The spatial pattern of water table depth at day 14 and following events changes as the direction of saturated lateral flow between the grids changes.
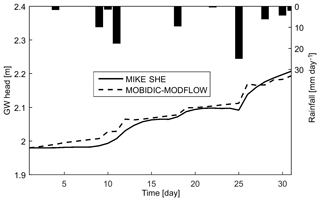
Figure 11Simulated water table depth by MIKE SHE (solid lines) and MOBIDIC–MODFLOW (dashed lines) at the outlet grid of Borden catchment.
Hence, the saturated flow exchange between the zones with different characteristics of the interaction between the UZ and SZ (zone 1 with inverse relation between the unsaturated and saturated storage, and zone 2 with a direct relationship between them as classified in the Introduction) can affect the overall behaviour of the water table fluctuations at the catchment scale. In Fig. 11, the water table changes (sharp in MIKE SHE and smooth in MOBIDIC–MODFLOW) are related to the calculation of groundwater recharge in two models. Equation (19) (revised groundwater recharge) shows that in the revised version of MOBIDIC–MODFLOW, the groundwater recharge is zero during days without infiltration. This means that the response of the water table to the fallen precipitation is rapid, and the unsaturated moisture profile quickly reaches its equilibrium state as discussed in Sect. 5. Therefore, on rainy days, the MOBIDIC–MODFLOW water table quickly rises as opposed to that of MIKE SHE, in which the groundwater recharge is determined from the solution of the Richards equation and the soil profile may take a longer time before reaching its equilibrium state. Note that the slight increase in the water table level of MOBIDIC–MODFLOW between days 14 and 18 (no rainfall period) is due to the incoming lateral saturated flow from adjacent cells. That is why the predicted water able in MOBIDIC–MODFLOW is still slightly rising between 2 rainy days (from day 12 to day 17 and day 19 to day 24), as shown in Fig. 11. Consequently, the simulated water tables of the two models gradually converge in the days following a rainfall event (for example between the days 14 to 17 and 19 to 24) as the transient behaviour simulated by MIKE SHE dissipates following a long redistribution period.
The quick rise of the shallow water table in response to the precipitation was also observed in the experimental work of Abdul and Gillham (1984). In their study, the water table response of a sandy soil packed in a 160 cm×120 cm×8 cm box with a 12∘ surface slope with different initial water table levels under a uniform rainfall rate was investigated. The objective of the experiment was to evaluate the effect of the capillary fringe on the rise in the water table and on streamflow generation. The results revealed that when the water table is very shallow, that is, for the downhill regions of the slope where the capillary fringe extended to the soil surface, the water table rise was much greater than expected by the constant specific yield. The uphill regions, with a deeper water table depth, however, showed a delayed response due to the presence of the moisture deficit in the unsaturated zone. The simulated responses using MIKE SHE and MOBIDIC–MODFLOW (Fig. 8) are consistent with the findings of Abdul and Gillham (1984), attesting to their capability in capturing the effect of the capillary fringe on the water table rise. Note that the coefficient ω in MOBIDIC–MODFLOW (Eq. 19) changes as the water table level rises and falls, and, therefore, each computation grid in Fig. 8 has a different value for ω at each time step.
Comparing the simulated water table levels of the two models at Borden catchment (Figs. 10 and 11) attests to the soundness of the proposed UZ–SZ interaction scheme of MOBIDIC–MODFLOW at the catchment scale. The mean absolute error of the predicted water table by MOBIDIC–MODFLOW compared to MIKE SHE for the outlet grid cell is 0.013 m. As the water table rises, the water table could be much shallower than expected by the ultimate value for the specific yield (θsat−θfld). Therefore, the inclusion of a water-table-dependent specific yield in MOBIDIC–MODFLOW with the proposed groundwater recharge (Eq. 19) allowed for modelling of such a significant water table rise. Note that the modified MOBIDIC–MODFLOW does not have any additional calibration parameters, thereby the parameter uncertainties of the model remain unchanged. Comparison of the original and the modified equations of groundwater recharge in MOBIDIC (Eqs. 12 and 19, respectively) shows that both equations have only one calibration parameter (γ in Eq. 12 and ω in Eq. 19). The proposed modifications, however, have the advantage of eliminating the specific yield from the calibration parameters of MODFLOW using the expression dependent on the water table that is given in Eq. (18). The required soil hydraulic parameters for application of Eq. (18) are derived based on the soil texture database from Rawls et al. (1982). Therefore, the modified MOBIDIC–MODFLOW has one less calibration parameter (specific yield) compared with the original structure of the MOBIDIC–MODFLOW.
In addition, the proposed modifications in the conceptualisation of the unsaturated–saturated flow interaction of MOBIDIC–MODFLOW have the capability to take into account the inverse relation between the unsaturated and saturated moisture storage using a conceptual and computationally efficient framework. Modelling of such cases has been mostly addressed using physically based numerical models in which the subsurface flow is described either using a three-dimensional variably saturated flow or a one-dimensional Richards equation in the unsaturated zone coupled to a three-dimensional saturated flow equation. However, the application of these complex models at the catchment scale can be cumbersome due to the required data and computational burden to run such models. On the other hand, the conceptual shallow water table unsaturated–saturated interaction schemes in the literature (e.g. Seibert et al., 2003) do not allow for capturing the different water table responses of different soil types to the fallen pulses of precipitation shown in Fig. 5. The coefficients of such conceptual models are often determined through the calibration process against a few water table observations, which does not represent the disparity in water table response of different soil types of the catchment. However, using responses of the physically based model MIKE SHE for the calibration of the new groundwater recharge, it has been possible to model, with a good computational efficiency, the difference in the water table response of different soil types of the catchment. Note that, although the coefficient of ω in Eq. (19) in MOBIDIC–MODFLOW was calibrated against the simulated water table responses of MIKE SHE, the model works independently. In this study, the purpose of comparing the water table responses of the two models in test cases was to verify whether MOBIDIC–MODFLOW can reproduce the catchment-scale simulated water table responses of MIKE SHE as the expected response of the catchment in the absence of water table measurements.
An important advantage of the coupled MOBIDIC–MODFLOW presented in this paper lies in its capability to investigate phenomena such as saturation excess runoff without expensive computational burden. With regard to the similarities in the formulation and numerical solution technique of saturated flow in MIKE SHE and MOBIDIC–MODFLOW, the computational efficiency of the revised MOBIDIC–MODFLOW model is related to the conceptualisation of the unsaturated flow and its interaction with the saturated zone. The physically based models such as MIKE SHE require very fine discretisation of the unsaturated soil domain and require short time steps to avoid numerical instabilities. In addition, the iterative unsaturated–saturated coupling method in each unsaturated zone time step can remarkably increase the execution time of the system. However, the proposed approach in MOBIDIC–MODFLOW works with identical time steps in both unsaturated and saturated zones, without discretisation of the soil layer, which greatly improves the computational process. For example, the execution time for the Borden case took 10 min using a PC Core i7 with 8 GB of RAM for MOBIDIC–MODFLOW, while taking 30 h with MIKE SHE. This clearly indicates why such alternative modelling approaches are attractive for watershed-scale modelling purposes.
It should be noted that, while the coefficient ω in Eq. (19) was determined for sand, loamy sand, sandy loam, and loam, the model was tested for sandy soils where the moisture retention in unsaturated zone is small and the assumption of a quasi-steady equilibrium moisture profile in the unsaturated zone is legitimate, as discussed by Bierkens (1998). For finer textured soils, however, such an assumption may be questionable, and, therefore, the approach presented in this study must be fully tested over a variety of soil textures to further evaluate its exactitude to broader watershed conditions. In addition to testing the proposed approach over a variety of soil textures, a next step will consist of extending the applicability of the approach against observations in real catchments where other hydrological processes, such as summer–fall evapotranspiration and spring snowmelt, affect groundwater recharge in shallow aquifers.
In this paper, we have presented a series of modifications to the conceptualisation of the unsaturated and saturated flows of MOBIDIC, a conceptual hydrologic model, to extend its applications to shallow water tables where an inverse relationship between the unsaturated and saturated moisture storage exists. The modifications were as follows: (1) replacement of the model's conceptual saturated flow scheme with MODFLOW, (2) revisiting the conceptualisation of the interaction between the unsaturated and saturated zones and calculation of groundwater recharge, and (3) inclusion of a dynamic specific yield based on the quasi-steady-state pressure profile in the unsaturated zone. The key variables in modelling of shallow water table regions are (1) groundwater recharge and (2) the specific yield. Groundwater recharge is usually considered to be a function of the unsaturated moisture state and is a fraction of infiltrated moisture into the unsaturated soil layer. However, in shallow water table cases, its value can be larger than infiltration due to the capillary fringe above the water table, which causes a quick and significant water table rise (Jayatilaka and Gillham, 1996). The specific yield in the shallow water table regions is no longer a constant soil property and significantly decreases as the water table reaches the soil surface. Investigation of such cases is mostly addressed using physical based models (e.g. Cloke et al., 2006) or using fully conceptual approaches (e.g. Seibert et al., 2003). Through the coupling of MODFLOW to MOBIDIC, we have modified the unsaturated–saturated flow interaction of the model based on the assumption of the quasi-steady pressure profile in the unsaturated zone as the water table changes. In turn, the static specific yield in MODFLOW could be replaced with the dynamic specific yield that is dependent on the water table, such as derived by Duke (1972). Such modifications allowed the rapid and dynamic water table responses of shallow water table regions to be adequately captured. Also, the groundwater recharge in the model was defined with a power-type equation whose parameter (ω) was determined using the WTF method along with the physically based MIKE SHE model for a homogeneous soil column with different initial water table levels under different rainfall intensities. The appropriateness of the proposed changes were evaluated by comparing the simulated water table responses of the model against those of MIKE SHE in a two-dimensional (single slope) case under a continuous uniform rainfall rate and in a three-dimensional quasi-real catchment case (simplified Borden catchment) over a month of a measured daily rainfall hyetograph. In the light of simulation results, the following conclusions can be derived:
-
Inclusion of a dynamic specific yield in investigation of shallow water table responses is essential. Indeed, when the water table is close to the soil surface, the significance of rise is much greater than expected based on the ultimate value of the specific yield, e.g. θsat−θfld, as investigated by Jayatilaka and Gillham (1996). While in MIKE SHE, this is accounted for by using the iterative water table correction method, in MOBIDIC–MODFLOW, this is addressed by assuming a hydrostatic equilibrium state between UZ and SZ. To the authors' knowledge, this has not been taken into account in simplified coupling of a hydrologic and a groundwater model.
-
The presented analysis showed a complex relation between the water table rise and the rainfall rate, soil type, and depth to water tables. The simulation over different rainfall rates and water table levels showed that fine-textured soils with a large capillary fringe (consequently small unsaturated soil moisture deficit) could have the water table at the soil surface even with a low rainfall intensity. This is important for the investigation of saturation excess runoff in lowland near river zones of the catchments. Therefore, it is important for the model to distinguish such differences in the expected water table responses of different soil types for its suitability at the catchment scale.
-
The comparison of the simulated water tables of the two models at Borden case (mean absolute error equals 1.3 cm) along with their execution times (30 h with MIKE SHE against 10 min with MOBIDIC–MODFLOW) clearly demonstrates the applicability of a simplified approach implemented in MOBIDIC–MODFLOW in investigation of the groundwater–surface-water interaction. Further improvements of the approach with inclusion of other hydrological processes such as the effect of evapotranspiration on parameterization of the (ω) in future work will enable its applicability in real, practical applications.
The digital elevation model (DEM) of the Borden catchment can be accessed from http://www.hpsc-terrsys.de (Centre for High Performance Scientific Computing in Terrestrial System HPSCTerrSys, 2019). The precipitation data can be obtained from Environment Canada, http://climate.weatheroffice.ec.gc.ca (Government of Canada, 2019), for the Borden AWOS station. The simulation results of MIKE SHE and MOBIDIC-MODFLOW are available from the corresponding author upon request.
MB, RL, and MN contributed to the development of the methodology. The simulations with MIKE SHE and modifications in MOBIDIC were made by MB. Preparation and revision of the manuscript were done by MB under the supervision of RL and MN.
The authors declare that they have no conflict of interest.
This research was partly funded by a Discovery Grant from the National Science and Engineering Research Council of Canada and by the Groupe de recherché sur l'eau de l'Université de Sherbrooke (GREAUS).
This paper was edited by Thom Bogaard and reviewed by two anonymous referees.
Abdul, A. S. and Gillham, R. W.: Laboratory Studies of the Effects of the Capillary Fringe on Streamflow Generation, Water Resour. Res., 20, 691–698, https://doi.org/10.1029/WR020i006p00691, 1984.
Abdul, A. S. and Gillham, R. W.: Field studies of the effects of the capillary fringe on streamflow generation, J. Hydrol, 112, 1–18, https://doi.org/10.1016/0022-1694(89)90177-7, 1989.
Beven, K. J., Lamb, R., Quinn, P., and Freer, R.: TOPMODEL, in: Computer Models of Watershed Hydrology, edited by: Singh, V. P., USA, Water Resources Publication, 627–668, 1995.
Bierkens, M. F. P.: Modeling water table fluctuations by means of a stochastic differential equation, Water Resour. Res., 34, 2485–2499, https://doi.org/10.1029/98WR02298, 1998.
Brooks, R. H. and Corey, A. T.: Hydraulic Properties of Porous Media, Tech. Rep., Agricultural Research Service, Soil and Water Conservation Research Division, and the Agricultural Engineering Dept., Colorado State Univ., Fort Collins, Colorado, 1964.
Camporese, M., Paniconi, C., Putti, M., and Orlandini, S.: Surface-subsurface flow modeling with path-based runoff routing, boundary condition-based coupling, and assimilation of multisource observation data, Water Resour. Res., 46, W02512, https://doi.org/10.1029/2008WR007536, 2010.
Castelli, F.: A simplified stochastic model for infiltration into a heterogeneous soil forced by random precipitation, Adv. Water Resour., 19, 133–144, https://doi.org/10.1016/0309-1708(95)00041-0, 1996.
Castelli, F., Menduni, G., and Mazzanti, B.: A distributed package for sustainable water management: a case study in the Arno Basin, in: Proceeding of The role of Hydrology in Water Resources Management, Capri, Italy, October 2008, IAHS, 327, 52–61, 2009.
Castillo, A., Castelli, F., and Entekhabi, D.: Gravitational and capillary soil moisture dynamics for distributed hydrologic models, Hydrol. Earth Syst. Sci., 19, 1857–1869, https://doi.org/10.5194/hess-19-1857-2015, 2015.
Castillo, A. E.: Spatiotemporal variability of hydrologic response: an entropy-based approach using a distributed hydrologic model, PhD thesis, Massachusetts Institute of Technology, USA, 189 pp., 2014.
Centre for High Performance Scientific Computing in Terrestrial System HPSCTerrSys: available at: http://www.hpsc-terrsys.de, last access: 7 April 2019.
Chenjerayi Guzha, A. and Hardy, T. B.: Simulating streamflow and water table depth with a coupled hydrological model, Water Science and Engineering, 3, 241–256, https://doi.org/10.3882/j.issn.1674-2370.2010.03.001, 2010.
Chung, I., Kim, N.-W., Lee, J., and Sophocleous, M.: Assessing distributed groundwater recharge rate using integrated surface water-groundwater modelling: application to Mihocheon watershed, South Korea, Hydrogeol. J., 18, 1253–1264, https://doi.org/10.1007/s10040-010-0593-1, 2010.
Cloke, H. L., Anderson, M. G., McDonnell, J. J., and Renaud, J.-P.: Using numerical modelling to evaluate the capillary fringe groundwater ridging hypothesis of streamflow generation, J. Hydrol., 316, 141–162, https://doi.org/10.1016/j.jhydrol.2005.04.017, 2006.
DHI: MIKE SHE User Manual, Volume 2, Reference Guide, Danish Hydraulic Institute, 372 pp., 2014.
Downer, C. W. and Ogden, F. L.: Appropriate vertical discretization of Richards' equation for two-dimensional watershed-scale modelling, Hydrol. Process., 18, 1–22, https://doi.org/10.1002/hyp.1306, 2004.
Duffy, C. J.: Semi-Discrete Dynamical Model for Mountain-Front Recharge and Water Balance Estimation, Rio Grande of Southern Colorado and New Mexico, in: Groundwater Recharge in a Desert Environment: The Southwestern United States, edited by: Hogan, J. F., Philips, F. M., and Scanlon, B. R., American Geophysical Union (AGU), 255–271, https://doi.org/10.1029/009WSA14, 2013.
Duke, H. R.: Capillary properties of soils-Influence upon specific yield, Trans. ASAE, 15, 688–691, 1972.
Dunne, T. and Black, R. D.: An Experimental Investigation of Runoff Production in Permeable Soils, Water Resour. Res., 6, 478–490, https://doi.org/10.1029/WR006i002p00478, 1970.
Dupuit, J.: Etudes théoriques et pratiques sur le mouvement des eaux courantes suivies de considérations relatives au régime des grandes eaux, au débouché à leur donner, et a la marche des alluvions dans les rivières à fond mobile Carilian-Goeury et Dalmont, France, 1848.
Government of Canada: Historical Climate data, available at: http://climate.weatheroffice.ec.gc.ca, last access: 7 April 2019.
Graham, D. and Butts, M. B.: Flexible Integrated Watershed Modeling with MIKE SHE, in: Watershed models, edited by: Frevert, D. and Singh, V., CRC Press, 245–271, 2005.
Guzha, A.: Integrating Surface and Sub Surface Flow Models of Different Spatial and Temporal Scales Using Potential Coupling Interfaces, PhD thesis, Utah State University, USA, 243 pp., 2008.
Harbaugh, A. W., Banta, E. R., Hill, M. C., and McDonald, M. G.: MODFLOW-2000, The U.S. Geological Survey Modular Ground-Water Model – User Guide to Modularization Concepts and the Ground-Water Flow Process, Open File Rep.00–92, 127 pp., 2000.
Healy, R. W. and Cook, P. G.: Using groundwater levels to estimate recharge, Hydrogeol. J., 10, 91–109, https://doi.org/10.1007/s10040-001-0178-0, 2002.
Hilberts, A. G. J., Troch, P. A., and Paniconi, C.: Storage-dependent drainable porosity for complex hillslopes, Water Resour. Res., 41, W06001, https://doi.org/10.1029/2004WR003725, 2005.
Jayatilaka, C. J. and Gillham, R. W.: A deterministic-empirical model of the effect of the capillary fringe on near-stream area runoff 1. Description of the model, J. Hydrol., 184, 299–315, https://doi.org/10.1016/0022-1694(95)02985-0, 1996.
Jones, J. P., Sudicky, E. A., Brookfield, A. E., and Park, Y.-J.: An assessment of the tracer-based approach to quantifying groundwater contributions to streamflow, Water Resour. Res., 42, W02407, https://doi.org/10.1029/2005WR004130, 2006.
Kollet, S., Sulis, M., Maxwell, R. M., Paniconi, C., Putti, M., Bertoldi, G., and Sudicky, E.: The integrated hydrologic model intercomparison project, IH-MIP2: A second set of benchmark results to diagnose integrated hydrology and feedbacks, Water Resour. Res., 53, 867–890, https://doi.org/10.1002/2016WR019191, 2017.
Kollet, S. J. and Maxwell, R.: Integrated surface–groundwater flow modeling: A free-surface overland flow boundary condition in a parallel groundwater flow model, Adv. Water Resour., 29, 945–958, https://doi.org/10.1016/j.advwatres.2005.08.006, 2006.
Markstrom, S., Niswonger, R., Regan, R., Prudic, D., and Barlow, P.: GSFLOW – Coupled Ground-Water and Surface-Water Flow Model Based on the Integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005), Open File Rep. 6-D1, 254 pp., 2008.
McDonnell, J. J. and Taylor, C. H.: Surface and subsurface water contributions during snowmelt in a small Precambrian Shield watershed, Muskoka, Ontario, Atmos. Ocean, 25, 251–266, https://doi.org/10.1080/07055900.1987.9649274, 1987.
Nachabe, M. H.: Analytical expressions for transient specific yield and shallow water table drainage, Water Resour. Res., 38, 1193, https://doi.org/10.1029/2001WR001071, 2002.
Neitsch, S. L., Arnold, J. G., Kiniry, J. R., and Williams, J. R.: Soil and Water Assessment Tool, Theoritical Documentation Version 2009, Technical Report No. 406, Texas Water Resources Institute, 647 pp., 2011.
Rawls, W. J., Brakensiek, D. L., and Saxtonn, K. E.: Estimation of soil water properties, T. ASAE, 25, 1316–1320, 1982.
Refsgaard, C. J. and Storm, B.: MIKESHE, in: Computer models of catchment hydrology, edited by: Singh, V. P., Water resources publications, 809–846, 1995.
Seibert, J., Rodhe, A., and Bishop, K.: Simulating interactions between saturated and unsaturated storage in a conceptual runoff model, Hydrol. Process., 17, 379–390, https://doi.org/10.1002/hyp.1130, 2003.
Shah, N., Nachabe, M., and Ross, M.: Extinction Depth and Evapotranspiration from Ground Water under Selected Land Covers, Ground Water, 45, 329–338, https://doi.org/10.1111/j.1745-6584.2007.00302.x, 2007.
Storm, B.: Modeling of Saturated Flow and the Coupling of Surface and Subsurface Flow, in: Recent advances in the modelling of hydrologic systems, edited by: Bowles, D. S. and O'Connell, P. E., Springer Netherlands, 185–203, https://doi.org/10.1007/978-94-011-3480-4_10, 1991.
VanderKwaak, J. E.: Numerical simulation of flow and chemical transport in integrated surface-subsurface hydrologic system, PhD thesis, University of Waterloo, Canada, 243 pp., 1999.
- Abstract
- Introduction
- Water table fluctuation method
- Models description
- Water table fluctuation method for a soil column using MIKE SHE
- Changes in conceptualisation of the UZ–SZ interactions in MOBIDIC–MODFLOW
- Application of the modified unsaturated–saturated scheme of MOBIDIC–MODFLOW in two test cases
- Discussion
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Water table fluctuation method
- Models description
- Water table fluctuation method for a soil column using MIKE SHE
- Changes in conceptualisation of the UZ–SZ interactions in MOBIDIC–MODFLOW
- Application of the modified unsaturated–saturated scheme of MOBIDIC–MODFLOW in two test cases
- Discussion
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References