The probability distribution of daily precipitation at the point and catchment scales in the United States

Choosing a probability distribution to represent daily precipitation depths is important for precipitation frequency analysis, stochastic precipitation modeling and in climate trend assessments. Early studies identified the two-parameter gamma (G2) distribution as a suitable distribution for wet-day precipitation based on the traditional goodness-of-fit tests. Here, probability plot correlation coefficients and L-moment diagrams are used to examine distributional alternatives for the wet-day series of daily precipitation for hundreds of stations at the point and catchment scales in the United States. Importantly, both Pearson Type-III (P3) and kappa (KAP) distributions perform very well, particularly for point rainfall. Our analysis indicates that the KAP distribution best describes the distribution of wet-day precipitation at the point scale, whereas the performance of G2 and P3 distributions are comparable for wet-day precipitation at the catchment scale, with P3 generally providing the improved goodness of fit over G2. Since the G2 distribution is currently the most widely used probability density function, our findings could be considerably important, especially within the context of climate change investigations.

1 Introduction

Precipitation is paramount in the fields of hydrology, meteorology, climatology and others. However, long series of precipitation data are not always available; therefore, establishing a probability distribution that provides a good fit to daily precipitation depths has long been a topic of interest. Investigations into the probability distribution of daily precipitation can be found in at least three main research areas, namely, (1) stochastic precipitation models, (2) frequency analysis of precipitation and (3) precipitation trends related to global climate change. Table 1 displays a sampling of the literature related to those three topics, including the particular precipitation series and durations under investigation as well as the proposed probability distributions recommended. Table 1 is by no means exhaustive; it only attempts to document the widespread interest in the determination of a suitable distribution for daily precipitation totals in a wide range of studies across a wide range of fields of inquiry.

1.1 Stochastic precipitation models

Our central goal is to select a suitable generalized probability distribution for modeling daily precipitation depths; thus, we are only concerned with the class of “two-part” stochastic daily precipitation models that utilize a probability distribution function to describe precipitation amounts on wet days, while a probabilistic representation of precipitation occurrences can be separately described using a Markov model or some form of a stochastic renewal process (Buishand, 1978; Geng et al., 1986; Waymire and Gupta, 1981; Watterson, 2005). We only consider the selection of a suitable distribution for modeling wet-day daily rainfall, leaving the stochastic representation of the occurrence of zeros to others.

Table 1 Review of literature pertinent to daily precipitation probability distribution selection.

It is evident from Table 1 that the wet-day precipitation series is the primary series considered within the stochastic precipitation model literature. Thom's (1951) suggestion of the two-parameter gamma (G2) distribution function for wet-day amounts seems to carry considerable weight. Buishand (1978) lent support to the suggestion of the G2 distribution by showing that for the wet-day series at six stations, the empirical ratio of the coefficient of variation to coefficient of skewness was quite close to the theoretical value of 2 for a G2 distribution. Geng et al. (1986) provided a review of other literature supporting the use of the G2 distribution for modeling wet-day rainfall.

While the G2 distribution is by far the most commonly advocated distribution for wet-day precipitation amounts, other distributions have also been suggested. Woolhiser and Roldan (1982), Wilks (1998) and Li et al. (2013) suggested the use of a three-parameter mixed exponential distribution instead of G2. Through a variety of goodness-of-fit tests and log-likelihood analyses, the mixed exponential was preferred to G2 (Wilks, 1998).

The Weibull (W2) and to a lesser extent the exponential distribution have also been suggested for modeling daily precipitation amounts (Duan et al., 1995; Burgueno et al., 2005). Duan et al. (1995) used a Chi-squared test to demonstrate that synthetic rainfall generated from the W2 and G2 models best match the observed daily rainfall data within each month. Burgueno et al. (2005) used graphical methods and the Kolmogorov–Smirnov test to give support to the W2 and exponential distributions.

1.2 Precipitation frequency analysis

The second section of Table 1 displays a small portion of the literature related to precipitation frequency analyses. Since extreme rainfall values are of primary importance in these studies, censored series of rainfall (e.g. the annual maximum series – AMS – and partial duration series – PDS) are often useful in these analyses (Stedinger et al., 1993). Table 1 displays that many of the precipitation frequency investigations of daily precipitation depths have selected the AMS series.

For many years, the most common approach to summarizing precipitation frequency analyses in the US was the work of Hershfield (1961), which is commonly referred to as TP-40. Hershfield (1961) fitted a Gumbel distribution to the AMS of 24 h precipitation. In the context of a national revision to the TP-40, Bonnin et al. (2006) fitted a generalized extreme value (GEV) distribution to the AMS of rainfall.

While the results of Bonnin et al. (2006) apply to the United States, other researchers have found similar results using similar methods in other parts of the world. Pilon et al. (1991) used L-moment goodness-of-fit results to show that the Gumbel distribution should be rejected in the favor of the GEV in Ontario, Canada. In Korea, Park and Jung (2002) successfully used the kappa distribution (of which the GEV is a special case) to generate extreme precipitation quantile maps. In perhaps the most comprehensive assessment of the distribution of precipitation extremes, Papalexiou and Koutsoyiannis (2013) examined the goodness of fit of the GEV distribution to a global data set of AMS. Analysis of such a large data set enabled them to conclude that GEV models of AMS of daily precipitation provide a good approximation.

Interestingly, while a great deal of attention is given to fitting distributions to the relatively short AMS series of precipitation depths, very few studies directly explore the probability distribution of the complete series of daily precipitation (including zeros) or the wet-day series of daily precipitation (zeros excluded). Shoji and Kitaura (2006) investigated both complete and wet-day daily precipitation series, but included only the normal, lognormal, exponential, and W2 distributions as candidate distributions, and did not employ modern regional hydrologic methods such as the method of L-moments. Deidda and Puliga (2006) investigated the degree of left-censoring of wet-day series needed to fit a generalized Pareto (GPA) distribution for 200 stations in Italy with a range of modern statistical analysis techniques. Wilson and Toumi (2005) derived a fundamental distribution for heavy rainfall, with a simple expression for rainfall as the product of mass flux, specific humidity and precipitation efficiency. Statistical theory predicted that the tail of the derived rainfall distribution has a stretched exponential form with a shape parameter of two-thirds, which was verified by a global daily precipitation data set.

Perhaps the most thorough investigations, to date, on the probability distribution of daily precipitation amounts are the global studies by Papalexiou and Koutsoyiannis (2012, 2016). Papalexiou and Koutsoyiannis (2012) derived a generalized gamma (GG) distribution from entropy theory, using plausible constraints for wet-day series of daily precipitation series. Together, the two studies by Papalexiou and Koutsoyiannis (2012, 2016) revealed that the GG distribution provides a good approximation of the behavior of observed L-moments of global series of wet-day daily precipitation at 11 519 and 14 157 stations, respectively. The GG distribution was also used in stochastic modeling of precipitation; see Fig. 5 for hourly and Fig. 6 for daily in Papalexiou (2018). Actually any distribution that describes wet-day precipitation (or at any other scale) well can be used as this stochastic modeling scheme; this makes it feasible to use any probability distribution and any correlation structure.

1.3 Precipitation trends and changes

The third section of Table 1 summarizes a small portion of the precipitation trend literature, which has become a rather large area of inquiry due to concerns over climate change, as evidenced from recent reviews on the subject (Easterling et al., 2000; Trenberth, 2011; Madsen et al., 2014). Almost universally, the G2 distribution appears to be accepted without serious consideration of alternative distributions. For instance, Groisman et al. (1999) compared maps of the empirical probability of summer 1-day rainfall exceeding 50.4 mm with maps of probabilities determined by a stochastic model using the fitted G2 distribution for the amounts. They found acceptable fits in regions where there are enough observed daily rainfall events greater than 50.4 mm.

This is an interesting contrast to the precipitation frequency analysis literature where a G2 distribution is often fit to wet-day series for the purpose of examining extreme rainfall instead of using the AMS series fitted by a GEV or other distribution. Yoo et al. (2005) explained that conventional frequency analysis (using AMS) cannot expect to predict precipitation changes resulting from climate change, while an examination of the differences in the G2 distribution's parameters (fitted to the whole wet-day record) might predict such changes. They found that modifying the parameters of the daily G2 distribution can explain changes in rainfall quantiles predicted by general circulation models under various climate change scenarios.

In a national study of precipitation trends, Karl and Knight (1998) employed the G2 distribution to fill in missing precipitation observations. Both Watterson and Dix (2003) and Watterson (2005) assumed a G2 distribution for daily precipitation in the development of stochastic rainfall models for use in evaluating changes in precipitation extremes.

Figure 1 Map showing locations of (a) 237 precipitation gaging stations and (b) 305 catchments.

1.4 Research objectives

In summary, there are a wide variety of previous studies which have explored the probability distribution of daily precipitation for the purposes of precipitation frequency analysis, stochastic precipitation modeling and trend detection. There seems to be a consensus that annual maxima appear to be well approximated by either a GEV or Gumbel probability density function (pdf), while peaks above threshold values are well approximated by a GPA distribution, and the series of wet-day precipitation is well approximated by a G2, GG, W2 or in some cases a mixed exponential distribution. However, other than the two recent global studies by Papalexiou and Koutsoyiannis (2012, 2016), we are unaware of any studies that have used recent developments in regional hydrologic frequency analysis such as L-moment diagrams or probability-plot goodness-of-fit evaluations to evaluate the probability distribution of very large regional data sets comprised of the wet-day series of daily precipitation.

Figure 2 Distribution of full record length of point precipitation based on weather stations.

The recent studies by Papalexiou and Koutsoyiannis (2012, 2016) represent perhaps the most comprehensive studies to date. However, their L-moment evaluations only evaluate the relationship between L-skewness and L-Cv; thus they were unable to fully evaluate the goodness of fit of the several relatively new three-parameter pdfs introduced in their studies such as the GG and the Burr type XII pdfs, which would require construction of L-kurtosis versus L-skew diagrams, which are currently unavailable for those pdfs. Analogous to those two studies, this paper uses two large-scale national data sets to re-examine the question of which of the commonly used continuous distribution functions which are widely used in the fields of hydrology, meteorology and climate best fit wet-day series of observed daily precipitation data. We focus our research interest on the distribution of wet-day series of precipitation since the pdf of complete series can be derived by a mixed distribution consisting of a combination of the pdf of wet-day series and a stochastic model of the percentage and occurrence of zeros.

Instead of considering the GG distribution, the pdf recommended by both Papalexiou and Koutsoyiannis (2012, 2016), which has seen very limited use and for which analytical and/or polynomial relationships for L-kurtosis are unavailable (as they are for most commonly used pdfs in hydrology), we consider the more widely used three-parameter generalization of the G2 distribution known as the Pearson type III (P3) distribution. Our primary objective is to use a very large national spatially distributed data set at both the point and catchment scales, to determine a suitable probability distribution of wet-day series of daily precipitation using L-moment diagrams and probability-plot correlation-coefficient goodness-of-fit statistics.

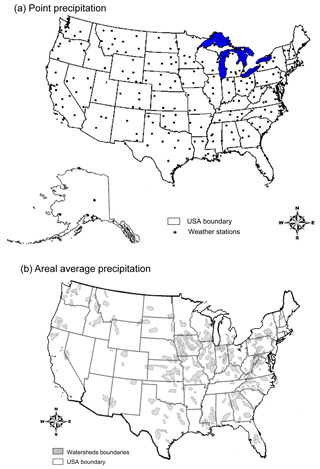
Figure 3 Distribution of wet-day record length: (a) point precipitation and (b) areal average precipitation over watersheds. Days with zero precipitation are removed in the wet-day records.

Figure 4 L-Cv vs. L-skew L-moment ratio diagram of sample L-moments and theoretical distributions: (a) point precipitation and (b) areal average precipitation depths.

2 Study area and data

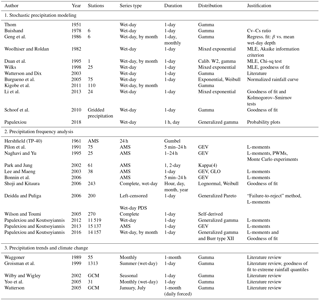
Precipitation depths at the point and catchment scales provide important information in hydrology, meteorology and other fields; thus, our study focuses on both scales. For point precipitation, we employ a data set comprised of daily precipitation depths at 237 first-order NOAA stations from 49 US states (Hawaii is excluded due to fundamentally different precipitation behavior). Station locations are shown in Fig. 1a. In contrast, the areal average precipitation for 305 catchments in the international Model Parameter Estimation Experiment (MOPEX) data set (Duan et al., 2006) is also selected for analysis. The catchment locations and boundaries are shown in Fig. 1b. The data were quality controlled to remove null values. When more than six null values occurred in a given year or more than three in a given month, the full year of data was removed. When fewer than these numbers of null values were present, they were treated as zeroes. The average record length for point precipitation depths for the 237 sites is 24 657 days (67.5 years). The distribution of record lengths corresponding to the 237 first-order NOAA stations is shown in Fig. 2. The MOPEX data set consists of 56 years of areal average daily precipitation from 1948 to 2003, corresponding to a fixed record length of 20 454 days for each of the 305 catchments shown in Fig. 1b.

The wet-day series were extracted from both data sets. The wet-day series were constructed by excluding zero and “trace” values (those with less than 0.01 in. – approximately equivalent to 0.25 mm – recordable precipitation). Wilks (1990) discussed other ways to treat trace precipitation and left-censored data, but for convenience, they are simply excluded. The mean wet-day record lengths for point and areal average precipitation are 7219 days (equivalent to nearly 20 years) and 14 043 days (more than 38 years), respectively. The distributions of wet-day record length are shown in Fig. 3. As expected, the proportion of wet days in the areal average precipitation data set is higher than that in the point precipitation data set.

3 Methodology

This section describes the methods of analysis used for assessing the goodness of fit of various distributional hypotheses, namely, L-moment diagrams and probability plot correlation coefficients.

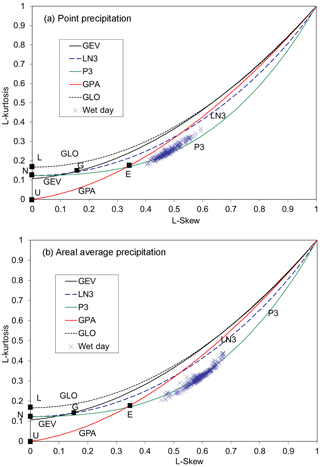
Figure 5 L-skew vs. L-kurtosis L-moment ratio diagram of sample L-moments and theoretical distributions: (a) point precipitation and (b) areal average precipitation depths. Logistic (L), normal (N), uniform (U), Gumbel (G), and exponential (E) distributions appear as a single point.

3.1 L-moment diagrams

L-moment diagrams are now a widely accepted approach for evaluating the goodness of fit of alternative distributions to observations. The theory and application of L-moments introduced by Hosking (1990) are now widely available in the literature (Stedinger et al., 1993; Hosking and Wallis, 1997); hence, they are not reproduced here.

The distribution of wet-day series of precipitation is highly skewed due to the large proportion of small non-zero values and high variance. Higher order conventional moment ratios such as skewness and kurtosis are very sensitive to extreme values and can exhibit enormous downward bias even for extremely large sample sizes (Vogel and Fennessey, 1993), as is the case here. However, L-moment ratios are approximately unbiased in comparison to conventional moment ratios, thus providing a particularly useful tool for investigating the pdf of daily wet-day precipitation series.

L-moment ratio diagrams provide a convenient graphical image to view the characteristics of sample data compared to theoretical statistical distributions. The L-moment diagrams, L-kurtosis (τ₄) vs. L-skew (τ₃) and L-Cv (τ₂) vs. L-skew (τ₃), enable us to compare the goodness of fit of a range of four-parameter, three-parameter, two-parameter and one-parameter (or special case) distributions. Table 2 displays distributions analyzed by means of the τ₄ vs. τ₃ L-moment ratio diagrams.

Table 3 displays distributions analyzed by means of the τ₂ vs. τ₃ L-moment ratio diagrams.

Table 2 Theoretical probability distributions presented on the L-kurtosis vs. L-skew L-moment diagram.

Note that α, β and γ are parameters used for location, scale and shape, respectively; if more than one parameter of the same type exists, indices (e.g. γ₁, γ₂) are used.

Table 3 Theoretical probability distributions presented on the L-Cv vs. L-skew L-moment diagram.

Note that α, β and γ are used for location, scale and shape, respectively; if more than one parameter of the same type exists, indices (e.g. γ₁, γ₂) are used.

L-moment ratio diagrams have been used before to examine the distribution of series of annual maximum precipitation data (Pilon et al., 1991; Park and Jung, 2002; Lee and Maeng, 2003; Papalexiou and Koutsoyiannis, 2013) and left-censored records (Deidda and Puliga, 2006). Other than the two recent global studies by Papalexiou and Koutsoyiannis (2012, 2016), which examined the agreement between empirical and theoretical relationships between L-Cv and L-skew, this is the only study we are aware of in which a set of daily wet-day precipitation records have been subjected to such a comprehensive L-moment goodness-of-fit analysis. L-moment estimators were chosen in this study for a variety of reasons: (1) they are easily computed and nicely summarized by Hosking and Wallis (1997) for all the cases considered in this study, and (2) estimates of L-moments are unbiased and estimates of L-moment ratios are nearly unbiased, and thus for the extremely large sample sizes considered here, sampling variability of empirical L-moment ratios will be extremely small, especially when contrasted with the variability among the theoretical L-moment ratios corresponding to the various distributions considered.

3.2 Probability-plot correlation-coefficient goodness-of-fit evaluation

Probability plots are constructed for each of the wet-day series using L-moment estimators of the distribution parameters (see Hosking and Wallis, 1997) for the distributions indicated in Table 4. A probability plot is constructed in such a manner as to ensure that the observations will appear to create a linear relationship when they arise from the hypothesized distribution assumed for each plot.

The goodness of fit of each probability plot is summarized using a probability plot correlation coefficient (PPCC, or simply, r) which is simply a measure of the linearity of the plot. The PPCC statistic has a maximum value of 1. The PPCC has been shown to be a powerful statistic for evaluating the goodness of fit of a wide range of alternative distributional hypotheses (Stedinger et al., 1993) and for performing hypothesis tests of various two-parameter distributional alternatives.

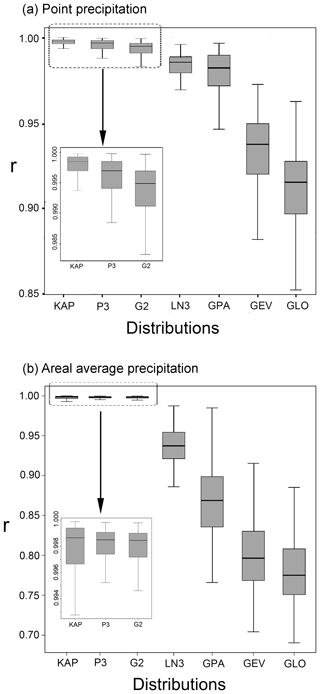
Figure 6 Standard box plots of r for all 7 distributions evaluated for wet-day series of (a) point precipitation and (b) areal average precipitation depths.

To construct a probability plot and to estimate a PPCC requires estimation of a plotting position. There are two classes of plotting positions, those that yield unbiased exceedance probabilities and those that yield unbiased quantile estimates. The Weibull plotting position given by $p=i/(n+\mathrm{1})$ yields an unbiased estimate of exceedance probability regardless of the underlying distribution (see Stedinger et al., 1993). Alternatively, there would be a unique plotting position to use for each probability distribution, and it is now well known that unbiased plotting positions for three parameter distributions require an additional parameter to estimate within the plotting position. For example, Vogel and McMartin (1991) derived an unbiased plotting position for the P3 distribution which depends upon the skewness of the distribution, a parameter which adds so much additional uncertainty to the analysis that it led Vogel and McMartin (1991), after considerable analysis, to not recommend its use. To put all the distributional alternatives on the same footing, we chose to use the Weibull plotting position for estimation of all PPCC values.

4 Results and analysis

4.1 L-moment diagrams

4.1.1 L-Cv vs. L-skew

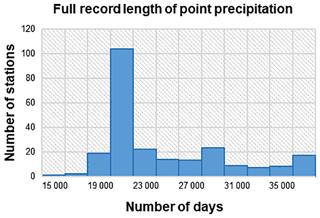
Figure 4 displays empirical and theoretical distributional relationships between L-Cv and L-skew for point values of daily precipitation (Fig. 4a) and areal average values of daily precipitation (Fig. 4b). The various curves represent the theoretical relationship between L-Cv and L-skew for the distributions indicated. Each plotted point represents the empirical relationship between L-Cv and L-skew for a single precipitation station or catchment. By comparing the empirically derived points with the theoretical curves, it is possible to see the degree to which the distributional tail behavior of the data record matches those of the candidate distributions. We emphasize again, importantly, that the sample sizes are large enough in this study so that one may, approximately, ignore sampling variability in all L-moment diagrams. This phenomenon was nicely illustrated in Fig. 2 of Blum et al. (2017), using synthetic data, for record lengths similar to those used here, but corresponding to daily streamflow records.

Table 4 Distributions used in probability plot goodness-of-fit evaluations.

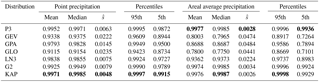
Table 5 Central tendency and spread of values of PPCC for the 237 precipitation stations and 305 catchments. Bold values are the optimal value of each column.

In Fig. 4a, the L-moment ratios fall primarily within a region bounded by the G2 and GP2 theoretical curves, with the W2 passing through some of the points. In Fig. 4b, the L-moment ratios fall primarily in the upper region of the W2 theoretical curve, with the G2 passing through or very close to most of the points. These patterns do not indicate a clearly preferred distribution for point values, especially considering that the large sample sizes associated with these series result in negligible sampling variability. However, Fig. 4b documents that the G2 pdf provides a good approximation to the pdf of wet-day series for areal average values.

Blum et al. (2017, Fig. 2) used L-moment diagrams for complete and synthetic series of daily streamflow observations to demonstrate that the sampling variability in L-moment ratios is negligible for the sample sizes considered in this study. Thus, the scatter shown in Fig. 4 is likely due to real distributional differences rather than due to sampling variability as is often the case when one constructs L-moment diagrams for short AMS precipitation and streamflow records, as is the case in most previous studies which have employed L-moment ratio diagrams.

4.1.2 L-kurtosis vs. L-skew

Figure 5 displays empirical and theoretical distributional relationships between L-kurtosis vs. L-skew point values of daily precipitation (Fig. 5a) and areal average values of daily precipitation (Fig. 5b). It should be noted that the P3 distribution is the two-parameter G2 with an additional location parameter which does not affect the shape characteristics and thus the theoretical curve of P3 shown in Fig. 5 is the same as the G2. The same holds for GPA and GP2 and for LN2 and LN3. The empirical relationships of plotted points for both wet-day series are very similar to the theoretical relationship for the P3 distribution. In fact, among the pdfs considered in Fig. 5, the P3 pdf seems to be the only three-parameter distribution that could possibly fit the wet-day record data. Although there is a small proportion of points lying outside the P3 curve, the overall fit is still very striking.

It should also be noted that the L-moment ratio estimates for both wet-day series occupy a space that can be well represented by the KAP distribution, which occupies a region of the L-kurtosis vs. L-skew diagram as shown in Fig. A1 of Hosking and Wallis (1997). A complete description of the four-parameter KAP distribution can be found in Hosking (1994) and Hosking and Wallis (1997).

4.2 Probability plot correlation coefficient

4.2.1 Standard box plots of PPCC

The L-moment ratio diagrams were useful for identifying several potential candidate distributions for representing the wet-day daily precipitation series at the point and catchment scales. From that analysis, we conclude that a four-parameter kappa pdf is needed to approximate the pdf of point wet-day series whereas a G2 and P3 pdf are adequate to approximate the pdf of areal average wet-day series. The PPCC statistic offers another quantitative method for comparing the goodness of fit of different distributions to the daily precipitation observations. Table 5 summarizes the central tendency and spread of the values of PPCC for each of the distributions for the wet-day series of point- and catchment-scale daily precipitation, respectively. The highest values for the mean, median, 95th percentile and 5th percentile of the PPCC are shown in bold type. The lowest values of the sample standard deviation of the PPCC values, denoted $\widehat{s}$, are also shown in bold. Figure 6 illustrates box plots of the values of PPCC for distributions fitted to the wet-day series of daily precipitation data at the point and catchment scales.

Figure 6 and Table 5 indicate that for the wet-day series of point daily precipitation depths, all the distributions have median PPCCs well above 0.9, but only the median PPCCs of G2, P3 and KAP distributions are over 0.99. The same situation appears in the catchment-scale precipitation, except that the median PPCCs of the remaining four distributions are significantly lower than the corresponding values for point precipitation.

The insets in Fig. 6 show detailed views of the box plots of PPCC values for the G2, P3 and KAP distributions for point and areal average daily precipitation. From Fig. 6a, KAP distribution results in the best goodness of fit for point precipitation because all of its indices are the best, while the P3 distribution generally performs better than the G2 distribution. However, for catchment-scale precipitation (Fig. 6b), the four-parameter KAP distribution is no longer competitive, and both the G2 and P3 pdfs will suffice. We are reluctant to advocate the use of a four-parameter pdf, such as the KAP distribution, due to its inherent complexity, though such a pdf may be needed for point values, as evidenced from our analyses.

4.2.2 Graphical comparison of P3, G2 and KAP

Across all previous comparisons, the P3, G2 and KAP are the best-fitting distributions for describing daily precipitation at the point or catchment scales. The insets in Fig. 6 identify the distributions that exhibit the best fit to each observed series. However, these inserts do not indicate by how much the best-performing distribution outperforms the second or third best. For this purpose, pairwise comparisons of the PPCC values of two highly performing distributions for all the stations and catchments are instructive. A simple graphical method can accomplish this goal.

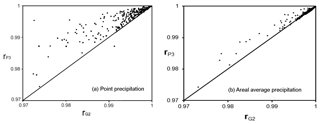
Figure 7 Comparison of PPCC (r) values for the P3 (vertical axis) and G2 (horizontal axis) distributions for the (a) point, and (b) areal average precipitation depths series. Points lying above the line represent stations with a higher r for the P3 distribution than G2 distribution.

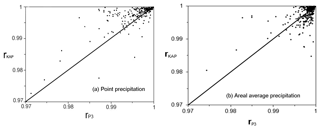
Figure 8 Comparison of r values for P3 (horizontal axis) and KAP (vertical axis) distributions for the (a) point and (b) areal average precipitation depths' wet-day series.

Figure 7 compares the PPCC values of the P3 (vertical axis) and G2 (horizontal axis) distributions for point- and catchment-scale daily precipitation. Approximately 98 % of stations are displayed in the figure; the remaining points lie outside the plot domains. Points lying above the diagonal line indicate that the P3 distribution has a higher PPCC for that particular station, and points lying below the diagonal line indicate the G2 results in a higher PPCC. Figure 7a shows that in nearly every case, the P3 distribution outperforms the G2 distribution. When the G2 does outperform the P3, the PPCCs are both very high and nearly equal. The point-scale precipitation plot shows that the P3 distribution performs significantly better than the G2 distribution in many cases. Thus, we conclude the P3 distribution better represents wet-day daily point precipitation than the more commonly used G2 distribution in nearly every case. Figure 7b compares the PPCC values of P3 and G2 for the catchment-scale precipitation. The results are nearly the same as for the point-scale precipitation in the sense that most points are above the diagonal line, while, for a few catchments where G2 does outperform P3, the points lie on the dividing line, showing only very slight superiority.

Figure 8 displays similar plots comparing the KAP (vertical axis) and P3 (horizontal axis) distribution for point- and catchment-scale daily precipitation. It can be seen in Fig. 8a that the KAP distribution does not always outperform the P3 pdf, as one might expect given that it has an additional parameter. We are reluctant to advocate the KAP pdf given its additional model complexity combined with the fact that it does not appear to provide a uniform improvement, in either case, over the P3 pdf.

Figure 9 The spatial distribution of best daily precipitation distribution function.

5 Discussion

From the L-moment diagrams and PPCC comparisons we concluded that KAP can better capture the tail behavior of point wet-day series, though both P3 and G2 can provide reasonable approximations in many situations. In contrast, we found that a KAP pdf is not needed to approximate the behavior of areal average wet-day series, where instead, either a P3 or G2 model would suffice. In this section, we evaluate the relationship between these findings and the size of the catchments considered.

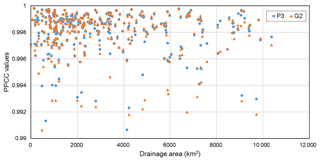
Figure 9 displays the PPCC values of P3 and G2 pdfs versus catchment drainage area for areal average wet-day series. The PPCC values are chosen from 0.99 to 1, approximately 96 % of catchments are displayed in the figure; the remaining points lie outside the plot domains. It can be seen that for most of the catchments, the PPCC values for G2 and P3 pdfs are very close, with points corresponding to G2 and P3 pdfs almost overlapping. This is especially true for PPCC values higher than 0.998. The phenomena clearly indicate that when G2 can represent the behavior of catchment-scale wet-day precipitation series well, P3 also provides very good performance. However, for the areas where PPCC values are lower than 0.996, the P3 distribution outperforms the G2 distribution for most cases, with a very slight improvement.

Figure 10 shows the spatial map of catchments with the corresponding best distribution functions for areal average wet-day series. KAP distribution is the best pdf for large proportion of the catchments, especially in the middle of the US. P3 distribution occupies the second large proportion of the catchments especially in the east-central US. Only a very few catchments can be best represented by G2 distribution. Seen from Fig. 10, it seems that the performances of the three pdfs vary greatly. However, as we have seen from previous figures, the differences between the three pdfs for catchments are very small.

6 Conclusions

This study has demonstrated that L-moment diagrams and probability plot correlation coefficient goodness-of-fit evaluations can provide new insight into the distribution of very long series of daily wet-day precipitation at both the point and catchment scales. Although previous studies have claimed that the commonly used two-parameter gamma distribution performs fairly well on the basis of traditional goodness-of-fit tests, this study reveals, through the use of L-moment diagrams and probability plot correlation coefficient goodness-of-fit evaluations that very long series of uncensored daily point and areal average precipitation are better approximated by a KAP distribution and a Pearson-III distribution respectively, and importantly, they do not resemble any of the other commonly used distributions. Analogous to the recent study by Papalexiou and Koutsoyiannis (2016), our evaluations yield very different conclusions than previous research on this subject and thus could have important implications for climate change investigations and other studies which employ a pdf of daily precipitation.

Figure 10 The spatial map of catchments with the corresponding best distribution functions for areal average wet-day series.

We conclude that for representing wet-day precipitation, the gamma and Pearson-III distributions are comparable with the four-parameter kappa distribution for the areal average precipitation; however, when the point precipitation is of concern, the kappa distribution should be the distribution of choice. We also conclude that future investigations should consider comparisons between the generalized gamma distribution introduced by Papalexiou and Koutsoyiannis (2012, 2016) for wet-day daily precipitation and the G2, Pearson type III and kappa distributions recommended here.

Once analytical and polynomial L-moment relationships and parameter estimation methods become available for the GG distribution, future studies should compare the P3 and GG distributions on wet-day series, because on the basis of this study, and Papalexiou and Koutsoyiannis (2016), the P3 and GG distributions appear to have tremendous potential for approximating the distribution of wet-day series.