Exploring the relationships between warm-season precipitation, potential evaporation, and “apparent” potential evaporation at site scale

Bouchet's complementary relationship and the Budyko hypothesis are two classic frameworks that are inter-connected. To systematically investigate the connections between the two frameworks, we analyze precipitation, pan evaporation, and potential evaporation data at 259 weather stations across the United States. The precipitation and pan evaporation data are from field measurement and the potential evaporation data are collected from a remote-sensing dataset. We use pan evaporation to represent “apparent” potential evaporation, which is different from potential evaporation. With these data, we study the correlations between precipitation and potential evaporation, and between precipitation and “apparent” potential evaporation. The results show that 93 % of the study's weather stations exhibit a negative correlation between precipitation and “apparent” potential evaporation. Also, the aggregated data cloud of precipitation vs. “apparent” potential evaporation with 5312 warm-season data points from 259 weather stations shows a negative trend in which “apparent” potential evaporation decreases with increasing precipitation. On the other hand, no significant correlation is found in the data cloud of precipitation vs. potential evaporation, indicating that precipitation and potential evaporation are independent. We combine a Budyko-type expression, the Turc–Pike equation, with Bouchet's complementary relationship to derive upper and lower Bouchet–Budyko curves, which display a complementary relationship between “apparent” potential evaporation and actual evaporation. The observed warm-season data follow the trend of the Bouchet–Budyko curves. Our study shows the consistency between Budyko's framework and Bouchet's complementary relationship, with the distinction between potential evaporation and “apparent” potential evaporation. The formulated complementary relationship can be used in quantitative modeling practices.

1 Introduction

Potential evaporation (E_p) is a widely used physical variable in hydrologic frameworks. It is the evaporation rate under unlimited land surface water supply (Thornthwaite, 1948). Pan evaporation (E_pan) measurement is often used as a surrogate of potential evaporation. However, these two variables are not the same (Brutsaert and Parlange, 1998; Roderick et al., 2009). A stipulation is added in the potential evaporation definition in Van Bavel (1966) and further clarified in Brutsaert (2015) that “the surface vapor pressure be saturated, so that it can be found from the surface temperature.” Therefore, the main difference between potential evaporation and pan evaporation is that pan evaporation is not measured under saturated surface vapor pressure. As a result, potential evaporation can be considered to depend only on the energy supply of climate, while pan evaporation is driven by both energy supply and humidity deficit in the atmosphere (Rotstayn et al., 2006). In Brutsaert and Parlange (1998), the term “apparent” potential evaporation (E_pa) is introduced to distinguish pan evaporation from potential evaporation. “Apparent” potential evaporation can be measured by an evaporation pan, while potential evaporation cannot. We acknowledge that there are different definitions of potential evaporation in the literature (Aminzadeh et al., 2016). Our study follows the definition of potential evaporation in Brutsaert and Parlange (1998) and Brutsaert (2015).

Because potential evaporation is energy-driven, it can be used as a physical variable to describe the energy supply in a hydrologic system. For instance, the well-established Budyko framework (Budyko, 1958, 1974) uses precipitation (P) and potential evaporation to represent the relationship between water supply and energy supply, and therefore to describe the impact of long-term climate on the hydrologic cycle. The Budyko framework has been extensively used to analyze interactions between hydrology, climate, vegetation, and other elements in watersheds (Milly, 1994; Zhang et al., 2001; Yang et al., 2007, 2011; Donohue et al., 2007; Xu et al., 2014; Zhou et al., 2015, 2016). Furthermore, the Budyko framework, which was originally applicable at the long-term mean annual scale, has been extended to shorter timescales, such as annual (Wang and Alimohammadi, 2012; Zhang et al., 2008) and intra-annual periods (Chen et al., 2013).

Several studies have made connections between the Budyko framework and Bouchet's complementary relationship (CR) (Bouchet, 1963). Yang et al. (2006) used the Fu equation (Fu, 1981), which is one of the commonly used equations to represent the Budyko curve, to describe the relationship between actual evaporation and potential evaporation in the CR. Roderick et al. (2009) presented a complementary relationship normalized by net irradiance and compared it with the Budyko framework. Lhomme and Moussa (2016) combined the Turc–Pike equation (Turc, 1954; Pike, 1964), which is another commonly used Budyko-type equation, with the CR to show the dependence of the Budyko curve on the drying power of the air.

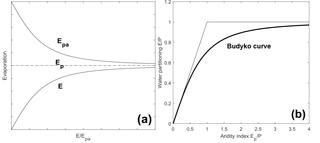
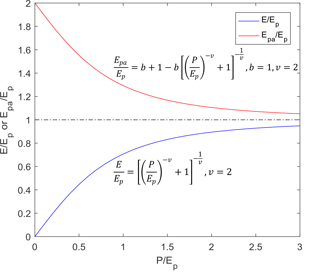
Figure 1 Conceptual representations of (a) the complementary relationship and (b) the Budyko framework.

When linking the Budyko framework with the CR, it is crucial to have a clear definition of different types of evaporation used in these two frameworks. Brutsaert and Parlange (1998) and Brutsaert (2015) generalized the CR and provided definitions of the evaporation terms in the CR, namely actual evaporation (E), potential evaporation (E_p), and “apparent” potential evaporation (E_pa; see Fig. 1a). Brutsaert and Parlange (1998) point out that the complementary relationship is between actual evaporation and “apparent” potential evaporation, not between actual evaporation and potential evaporation. In the Budyko framework (Fig. 1b), the definition of potential evaporation follows Van Bavel (1966)'s potential evaporation definition that it is under unlimited land surface water supply without the effect of humidity deficit (Budyko, 1974), which is the same as the E_p definition in the generalized CR. The definitions of evaporation, potential evaporation, and “apparent” potential evaporation in these different frameworks are summarized in Table 1.

Table 1 Types of evaporation in the Budyko framework and the original CR, and their redefined evaporation type based on a generalized CR. The last column refers to the definitions of the three types of evaporation in the generalized CR provided in Brutsaert (2015).

Process-based speaking, the CR suggests a connection between evaporation and “apparent” potential evaporation (Fig. 1a), which is driven by the energy feedbacks between atmosphere and land surface. During the drying process at the land surface, the excessive energy that is not used for evaporation will be available for the increase in sensible heat. The rise in air temperature will lead to an increase in the rate of “apparent” potential evaporation (Brutsaert and Parlange, 1998; Brutsaert, 2005; Aminzadeh et al., 2016). This connection between E_pa and E also suggests a connection between E_pa and P, since the water supply from precipitation will affect the rate of evaporation. In terms of the Budyko framework, E_p and P are used as the representations of energy supply and water supply, respectively. The ratio between E_p and P is the primary controlling factor of the ratio of E over P in watersheds at the long-term mean annual timescale (Fig. 1b). The ratio of E_p over P is also called the aridity index, which represents the dryness of the climate in a watershed. The ratio of E over P increases with the increase in the aridity index, indicating that more water from precipitation will become evaporation rather than runoff under a drier climate (Arora, 2002). No connection between E_p and P is suggested in the Budyko framework.

In order to explore the connections between the Budyko framework and the CR, our study investigates the relationships between precipitation and potential evaporation as well as between precipitation and “apparent” potential evaporation. We collect warm-season precipitation, potential evaporation, and pan evaporation data from 259 weather stations across the contiguous US. Studying the relationships between P, E_p, and E_pa advances our understanding of the well-established classic Budyko framework and the CR. Furthermore, based on insights provided by previous studies (Yang et al., 2006; Roderick et al., 2009; Lhomme and Moussa, 2016), we use a Budyko-type expression to develop a new formulation for the CR.

2 Methodology

2.1 Theoretical development

2.1.1 Budyko framework

The Budyko curve (Fig. 1b) describes the relationship between long-term water partitioning, represented by the ratio of actual evaporation over precipitation, and long-term climate, represented by the ratio of potential evaporation over precipitation, namely the aridity index (Budyko, 1958, 1974). In recent decades, the Budyko framework has been examined with annual data (e.g., Yang et al., 2007; Potter and Zhang, 2009; Cheng et al., 2011). A number of Budyko-type functions have been developed to mathematically describe the Budyko curve (Turc, 1954; Fu, 1981; Zhang et al., 2001; Yang et al., 2008; Wang and Tang, 2014). Within these functions, the Turc–Pike equation is a parsimonious single-parameter equation (Turc, 1954; Pike, 1964):

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{E}{P}}={\left[\mathrm{1}+{\left({\displaystyle \frac{E_{\text{p}}}{P}}\right)}^{-v}\right]}^{-\frac{\mathrm{1}}{v}},\end{array}$$

where E is actual evaporation, E_p is potential evaporation, P is precipitation, and v is a parameter to represent landscape properties such as vegetation coverage and soil properties (Zhang et al., 2001; Yang et al., 2008). The parameter v needs to be a positive number, and its typical value is 2.0.

2.1.2 Generalized complementary relationship

Bouchet's complementary relationship (Bouchet, 1963) describes the relationship between actual evaporation E and potential evaporation E_p. Brutsaert and Parlange (1998) introduced the term “apparent” potential evaporation E_pa and clarified that the CR is between E and E_pa, not E and E_p (Fig. 1a). They also proposed a generalized complementary relationship:

$$\begin{array}{}\text{(2)}& bE+E_{\text{pa}}=(\mathrm{1}+b)E_{\text{p}}\mathrm{0}\le E\le E_{\text{p}}\le E_{\text{pa}},\end{array}$$

where b is a proportionality parameter not less than one. When b is equal to one, Eq. (2) represents the original complementary relationship (Kahler and Brutsaert, 2006). “Apparent” potential evaporation will be higher than potential evaporation, especially under dry conditions, while it gradually approaches potential evaporation as the ratio of E over E_pa increases (Fig. 1a). As suggested by Morton (1976) and Brutsaert and Stricker (1979), potential evaporation can be estimated using the Priestley–Taylor equation (Priestley and Taylor, 1972), which is also called the equilibrium evaporation (Brutsaert and Chen, 1995; Jiang and Islam, 2001). “Apparent” potential evaporation can be estimated using the Penman equation (Penman, 1948; Linacre, 1994; Rotstayn et al., 2006) or using data measured at evaporation pans (Brutsaert, 1982; Brutsaert and Parlange, 1998):

$$\begin{array}{}\text{(3)}& E_{\text{pa}}=a{E}_{\text{pan}},\end{array}$$

where E_pan is the pan evaporation and a is the pan coefficient. The pan coefficient varies from location to location (Stanhill, 1976; Linacre, 1994). In Kahler and Brutsaert (2006), a pan coefficient of a=1.0 is recommended for mixed natural vegetation, which will be used in this study. It should be noted that the linear relationship between E_pa and E_pan given in Eq. (3) and the choice of “a” value will not affect the correlations between P, E_p, and E_pa.

2.1.3 Relationships between P, E_p, and E_pa

The x axis of the complementary relationship is a ratio between E and E_pa (Bouchet, 1963). Ramírez et al. (2005) used the water-energy framework to link the CR with the Budyko approach and changed the x axis in the CR to moisture availability. Following this idea, several studies have used precipitation or wetness index (P∕E_p) to represent moisture availability in the CR (Yang et al., 2006; Roderick et al., 2009). In this study, we also use P to represent moisture availability in the CR. E_p is a horizontal line in the CR that is parallel to the x axis (Fig. 1a). Therefore, the modified CR indicates that P and E_p are independent. On the other hand, the upper curve of the CR, representing “apparent” potential evaporation E_pa, declines along the x axis, indicating that E_pa and P are not independent. For a dimensionless CR, we normalize the x and y axes. The normalized CR describes the relationship between $\frac{E_{\text{pa}}}{E_{\text{p}}}$, $\frac{E}{E_{\text{p}}}$, and $\frac{P}{E_{\text{p}}}$ (Fig. 2).

Figure 2 Dimensionless Bouchet–Budyko curves in the normalized complementary relationship.

To connect the Budyko framework with the normalized CR toward formulating the Bouchet–Budyko curves, we first transform Eq. (1) into a relationship between $\frac{E}{E_{\text{p}}}$ and $\frac{P}{E_{\text{p}}}$:

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{E}{E_{\text{p}}}}={\left[{\left({\displaystyle \frac{P}{E_{\text{p}}}}\right)}^{-v}+\mathrm{1}\right]}^{-\frac{\mathrm{1}}{v}}.\end{array}$$

Yang et al. (2006) did a similar transformation using the Fu equation (Fu, 1981). Dividing both sides of Eq. (2) by E_p yields

$$\begin{array}{}\text{(5)}& b{\displaystyle \frac{E}{E_{\text{p}}}}+{\displaystyle \frac{E_{\text{pa}}}{E_{\text{p}}}}=\mathrm{1}+b.\end{array}$$

Combining Eqs. (4) and (5) gives a relation between $\frac{P}{E_{\text{p}}}$ and $\frac{E_{\text{pa}}}{E_{\text{p}}}$:

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{E_{\text{pa}}}{E_{\text{p}}}}=b+\mathrm{1}-{\left[{\left({\displaystyle \frac{P}{E_{\text{p}}}}\right)}^{-v}+\mathrm{1}\right]}^{-\mathrm{1}/v}{E}_{\text{pa}}\ge E_{\text{p}}.\end{array}$$

Equations (4) and (6) represent the lower and upper curves of the normalized CR, respectively (Fig. 2). Roderick et al. (2009) presented a similar framework, without the formulation of the curves. To verify the relationships between P, E_p, and E_pa, and to examine the Bouchet–Budyko curves in Eqs. (4) and (6), we analyze climate data from 259 weather stations across the contiguous US.

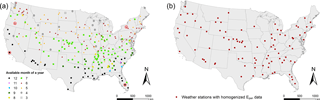
Figure 3 (a) Map of 259 weather stations. The available month of a year of pan evaporation data for each weather station is presented using legends with different colors and shapes. Four representative weather stations are selected from the four quadrants of the US, respectively, which are highlighted with red circles. (b) Map of 93 weather stations with homogenized pan evaporation data that overlap the 259-station dataset.

2.2 Data sources

Monthly precipitation and pan evaporation are collected from the National Oceanic and Atmospheric Administration (NOAA) at the National Climatic Data Center (NCDC). The data can be downloaded at https://www.ncdc.noaa.gov/IPS/cd/cd.html (last access: 17 August 2018). The precipitation data are measured using a standard rain gauge and the pan evaporation data using Class A evaporation pans. We collect data for the period 1984–2015 from a total of 259 weather stations (Fig. 3a). Since pan evaporation is collected only during warm months (when temperatures remain above freezing), the weather stations in cold regions have less than 12 months of pan readings in a year. We call the period of warm months in a year a “warm season”. We calculate the monthly average pan evaporation and precipitation using only the warm months for each year at each weather station. For short, they are called warm-season data (i.e., warm-season pan evaporation, warm-season precipitation). We also calculate the annually averaged warm-season data to represent the long-term average level of pan evaporation and precipitation at each station. For short, they are called long-term average data. Over the 259 selected stations, there is an average of 7 months per year with available pan evaporation data. As Fig. 3 shows, the number of available months decreases from the southern regions to the northern regions. For stations in the southern states with all 12 months of available data in a year, the full year will be considered a warm season. The northern state stations have fewer warm months, and, accordingly, the warm season is much shorter. On the other hand, not all 259 weather stations have the full record from 1984 to 2015; the average number of years with available data for each location is 18. A complete summary of the information available at all 259 weather stations is provided in Table S1 in the Supplement. In order to minimize the uncertainty from various warm periods in a year from station to station, we repeat the analysis using an alternative source of pan evaporation in the NCDC dataset containing homogenized warm month data from May to October (Hobbins, et al., 2017). A total of 93 weather stations overlap both sets of pan evaporation data for the period 1984 to 2001 (Fig. 3b). We convert pan evaporation in the NCDC dataset to “apparent” potential evaporation using Eq. (3).

The E_p data are collected from a remote-sensing dataset (Zhang et al., 2010), which is generated using the Priestley–Taylor equation with remotely sensed net radiation:

$$\begin{array}{}\text{(7)}& \mathit{\lambda }{E}_{\text{p}}=\mathit{\alpha }{\displaystyle \frac{\mathrm{\Delta }}{\mathrm{\Delta }+\mathit{\gamma }}}(R_{\text{n}}-G),\end{array}$$

where λ (J kg⁻¹) is the latent heat of vaporization; λE_p (W m⁻²) is the latent heat flux; α is a coefficient to account for the effect of surface characteristics and vegetation, and is set to 1.26; Δ (Pa ^∘C⁻¹) is the slope of the saturated vapor pressure curve; γ (Pa ^∘C⁻¹) is the psychometric constant; R_n (W m⁻²) is the net radiation; and G (W m⁻²) is the heat flux into the ground. The E_p data cover the period 1983–2006. Similarly to P and E_pa, we calculate the warm-season E_p and long-term annually averaged E_p based on the monthly E_p data.

2.3 P, E_p, and E_pa correlation analysis

Using the collected weather station data of precipitation and pan evaporation for the period 1984 to 2015, we first calculate the Pearson correlation coefficient between warm-season P and warm-season E_pa for each location (Fig. 3a). We then perform the same correlation analysis of P and E_pa using the homogenized pan evaporation dataset (Hobbins et al., 2017) (Fig. 3b). Secondly, we use data of warm-season P and warm-season E_p for the period of 1984 to 2006, which is the period when both P and E_p data are available, to investigate the correlation between P and E_p. Finally, to validate the newly derived Bouchet–Budyko curves, the relationship between $\frac{P}{E_{\text{p}}}$ and $\frac{E_{\text{pa}}}{E_{\text{p}}}$ is plotted using the collected data at both seasonal and long-term average timescales.

Figure 4 Map of the point-scale annual P–E_pa correlation at 259 weather stations: (a) r value and (b) p value.

3 Results

3.1 Correlations among P, E_p, and E_pa

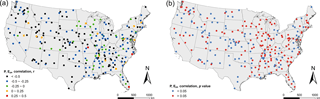
In the 259 weather stations, 93 % of the stations have a negative correlation between P and E_pa (Fig. 4a), but only 43 % of the stations are statistically significant (p<0.05; Fig. 4b). All significant P–E_pa correlations are negative. The weather stations located in the western region (regions with longitude higher than the weather station average longitude of 94.81^∘ W) are more likely to have a significant P–E_pa negative correlation than those located in the east (regions with longitude lower than 94.81^∘ W). This spatial difference may be related to climate characteristics: the eastern region has higher precipitation (average 105.5 mm month⁻¹) and lower “apparent” potential evaporation (average 145.3 mm month⁻¹), while the western region has lower precipitation (average 44.6 mm month⁻¹) and higher “apparent” potential evaporation (average 203.5 mm month⁻¹). Bouchet's complementary relationship is more significant in arid regions (Ramírez et al., 2005), corresponding to the left side of the CR curves, while it is less significant in humid regions, corresponding to the right side of the CR curves (Fig. 1a). As a result, the negative correlation between precipitation and “apparent” potential evaporation is more significant in the west than in the east.

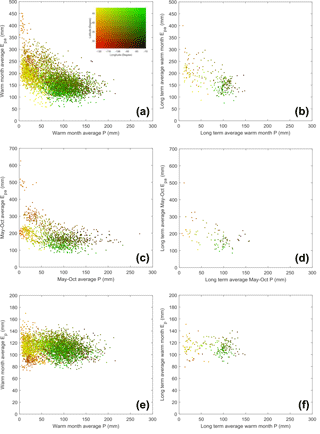
Figure 5 P vs. E_pa at 259 weather stations in the US for the period 1984 to 2015 for (a) warm-season data (N=5312) and (b) long-term annually averaged warm-season data (N=259). The data points are color-coded based on their latitudes and longitudes. P vs. E_pa at 93 weather stations in the US for the period 1984 to 2001 using the homogenized pan evaporation dataset for (c) the warm period May–October in each year (N=1214), and (d) long-term annual average warm period May–October data (N=93). P vs. E_p at the 259 weather stations for the period of 1984 to 2006 for (e) warm-season data (N=5312) and (f) long-term annual average warm-season data (N=259).

All the warm-season P vs. E_pa relations (i.e., all years, all seasons, for a total of 5312 data points) are shown in Fig. 5a. The data cloud shows a negative trend in general. We also plot the long-term annually averaged values of warm-season P and E_pa of the 259 weather stations (Fig. 5b), which shows a similar negative trend. Hobbins et al. (2004) showed a similar negative trend between precipitation and pan evaporation with watershed-scale data. To represent the spatial distribution of the weather stations, we color code the data points based on their spatial coordinates of latitude and longitude. The climate in the eastern US is much wetter than the western US, and therefore the data cloud of E_pa vs. P is separated into two parts horizontally. The right side of the cloud represents the northeastern and southeastern US (green and brown, respectively), while the left side of the cloud generally represents the northwestern and southwestern US (yellow and red, respectively).

As explained before, we also use an alternative pan evaporation dataset (Hobbins et al., 2017) to further validate our analysis result. This dataset is homogenized to have the same period of a pan evaporation data record in each year from May to October. In order to minimize the data heterogeneity caused by station move and human errors, this dataset compiled pan evaporation data from 247 stations across the US with thorough quality control. It is derived from the same dataset as our data, namely the NCDC dataset. Based on the homogenized pan evaporation data, 85 stations out of 93 (91 %) have a negative correlation between P and E_pa. Of these, 41 % of the stations have a statistically significant relationship (p<0.05), all negative. This result is consistent with the analysis result based on our collected data from 259 weather stations. We also use the data cloud to show the relationship between P and E_pa in the warm period of May to October in each year at each of the 93 stations (Fig. 5c), as well as the relationship of long-term annually averaged warm-period P and E_pa (Fig. 5d). The trend of the data cloud is similar to the data cloud trend using our collected data at both seasonal and long-term average timescales. In other words, both datasets show a negative relationship between P and E_pa.

The P and E_p data are shown in Fig. 5e, f. At both seasonal and long-term average timescales, there is no clear relationship shown between P and E_p, confirming the independence between P and E_p discussed in Sect. 2.1.3. This result shows the difference between E_p and E_pa, that E_p is independent of P but E_pa is not. Therefore, it is important to distinguish E_pa from E_p and to understand the different physical mechanisms of the two processes (Brutsaert, 2015).

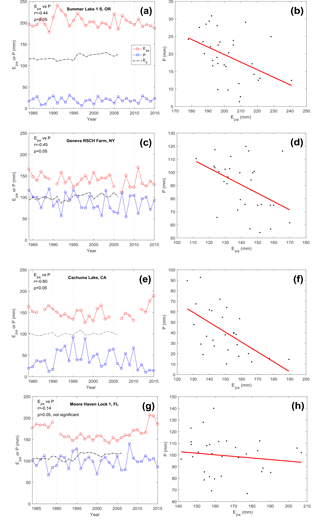
Figure 6 Warm-season P, E_p and E_pa time series of four example weather stations in the study period of 1984–2015: (a) Summer Lake 1 S, OR (42^∘58^′ N, 120^∘47^′ W); (c) Geneva RSCH Farm, NY (42^∘53^′ N, 77^∘20^′ W); (e) Cachuma Lake, CA (34^∘35^′ N, 119^∘59^′ W); (g) Moore Haven Lock 1, FL (26^∘50^′ N, 81^∘50^′ W); and the scatterplots of P vs. E_pa at the four example stations (b, d, f, h).

To present the P, E_p, and E_pa relationships at individual locations and therefore to further investigate the dependence between the three variables, we select four weather stations from the four quadrants of the contiguous US (Fig. 3a), to show the warm-season P, E_p, and E_pa in time series (Fig. 6). The two stations in the southern regions have data in all 12 months of a year, while the two stations in the northern regions only have E_pa data for 6 months of each year. All four stations show negative correlations between P and E_pa. This negative correlation at the weather station in Florida is not statistically significant (Fig. 6g, h). As mentioned before, the P and E_pa correlation is less significant in the eastern region than in the west, because of the wetter climate in the east. On the other hand, at the other three locations, the warm-season P and E_pa are relatively symmetric to each other (Fig. 6a–f). During years when one series is above average, the other tends to be below average and vice versa. In terms of the relationship between P and E_p, all four locations show no significant correlations between the two variables (p>0.05). This is consistent with the independence of P and E_p shown in Fig. 5e, f.

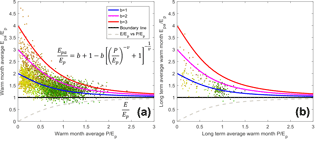
Figure 7 P∕E_p vs. E_pa∕E_p at 259 weather stations in the US for the period 1984 to 2015 for (a) warm-season data (N=5312) and (b) long-term average data (N=259). The data points are color-coded based on their latitudes and longitudes. The three upper Bouchet–Budyko curves are plotted with different b values of b=1, b=2, and b=3, and with the same v value of v=2. The dashed line is the lower Bouchet–Budyko curve with v=2.

3.2 Bouchet–Budyko curves

There are two Bouchet–Budyko curves (Fig. 2). The upper curve describes the relationship between E_pa, E_p, and P (Eq. 6) and the lower curve describes the relationship between E, E_p, and P (Eq. 4). The lower curve is derived from the Budyko curve based on the Turc–Pike equation. This relationship between E, E_p, and P has been studied extensively following the Budyko framework and, therefore, it is not the focus of this study. This study investigates the relationship between E_pa, E_p, and P, which is represented by the upper Bouchet–Budyko curve. Since the collected weather station data of P and E_pa are available from 1984 to 2015 and the E_p data collected from the remote-sensing dataset are available from 1983 to 2006, we examine the relationship between P∕E_p and E_pa∕E_p in the overlapping period of 1984 to 2006 (Fig. 7). Using Eq. (6) three curves with different b values (1, 2, and 3) are shown in Fig. 7. The v value is set at 2, which is commonly used in the Budyko framework. When b equals one, the two CR curves are symmetric. When b exceeds one, the two CR curves are asymmetric. This asymmetry is discussed in previous studies (Kahler and Brutsaert, 2006; Brutsaert, 2015). One explanation of this asymmetry between E and E_pa is that the evaporation pan will receive more heat than the surrounding area (Kahler and Brutsaert, 2006). Brutsaert (2015) reports an even higher b value of 4.5. The horizontal solid black line in Fig. 7 is the boundary of the upper Bouchet–Budyko curve, above which E_pa exceeds E_p.

4 Discussion

4.1 Relationship between P and E_pa, and between P and E_p

With the weather station data, a negative correlation between warm-season P and E_pa is shown in 242 out of the 259 weather stations (93 %). The negative correlation between P and E_pa is linked by the humidity deficit. The formation of precipitation is positively related to the local level of humidity (Pal et al., 2000; Sheffield et al., 2006; An et al., 2017), while “apparent” potential evaporation is inversely related to humidity or positively related to the humidity deficit (Penman, 1948; Allen et al., 1998). As a result, precipitation and “apparent” potential evaporation will tend to exhibit a negative correlation. According to Bouchet's complementary relationship, this negative correlation between P and E_pa is more pronounced in arid regions than in humid regions.

On the other hand, P and E_p show no significant correlation at both the seasonal and long-term average timescales. As a result, our study indicates that potential evaporation and precipitation, the representations of energy supply and water supply, are likely to be independent. This independence is currently under investigation with field data. It should be noted that the relationships between P and E_p and between P and E_pa found in this study are not direct causal relationships, but rather the result of interactions between a number of physical variables, such as net radiation, wind speed, humidity, and so forth. Further investigation into the physical mechanisms connecting these variables is underway.

4.2 The Bouchet–Budyko curve and its applications

Combining Bouchet's complementary relationship and the Budyko framework leads to two dimensionless CR curves, normalized by E_p (Fig. 2). The upper Bouchet–Budyko curve is derived from the connection between the Budyko framework and the CR, and the lower Bouchet–Budyko curve is derived directly from the Budyko framework, based on the Turc–Pike equation. The companion CR curves show that as the wetness index P∕E_p decreases, the difference between E and E_pa grows. This indicates the complementary relationship between E and E_pa is most pronounced in arid environments, that is, the CR is more significant under water-limited conditions. As discussed in Ramírez et al. (2005), the CR can be considered an extension of the Budyko framework.

The P, E_p, and E_pa collected in this study follow the general trend of the upper Bouchet–Budyko curve (Fig. 7). The remote-sensing data of E_p may not have the same level of accuracy as the field measured P and E_pa. The value of α in Eq. (7) may vary from location to location (Chen and Brutsaert, 1995; Brutsaert and Chen, 1995). Such factors may explain the deviation of some data points from the CR curve in Fig. 7.

This upper Bouchet–Budyko curve can be used to estimate the E_pa based on the data of P and E_p. The “apparent” potential evaporation can be measured by evaporation pan, but this measurement has its limitations. For example, it is only available for warm periods. The collected data with time-averaged pan evaporation levels over weeks, months, and years may lead to systematic error in surface flux calculations (Brutsaert, 1982; Kahler and Brutsaert, 2006). The Bouchet–Budyko curve can help us to estimate E_pa without the limitations of evaporation pans. Compared with more physically based E_pa quantification approaches, such as the Penman equation (Penman, 1948) and the “PenPan” model (Rotstayn et al., 2006), our equations are derived from conceptual frameworks and therefore may provide top–down insights into the E_pa level in hydrologic systems.

Similarly to the Budyko framework, the Bouchet–Budyko curves can be used in hydrologic models and climate models. These Bouchet–Budyko curves can be used to examine the fidelity of simulated precipitation and evaporation sequences routinely produced by general circulation models to drive climate change investigations.

5 Conclusions

We collected warm-season precipitation, potential evaporation, and “apparent” potential evaporation data at 259 weather stations in the US to investigate the correlation among these three physical variables. The results showed a negative correlation between P and E_pa at 93 % of the stations. The physical reason for the P–E_pa negative correlation could be related to the humidity variability. When humidity increases, the likelihood of precipitation increases while the rate of “apparent” potential evaporation decreases. On the other hand, our study results supported the assumption that P and E_p are independent. Combining the CR with a Budyko-type equation, we formulated the companion CR curves, showing the connection between the Bouchet and Budyko frameworks. These insights may encourage hydrologists to further explore the strong link between the Budyko framework and the CR, promoting new ways of hydrologic modeling. Future work will investigate the physical mechanisms behind the newly derived Bouchet–Budyko curves and explore the application of these companion curves.