the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Sensitivity of young water fractions to hydro-climatic forcing and landscape properties across 22 Swiss catchments
Jana von Freyberg
Scott T. Allen
Stefan Seeger
Markus Weiler
James W. Kirchner
The young water fraction Fyw, defined as the proportion of catchment outflow younger than approximately 2–3 months, can be estimated directly from the amplitudes of seasonal cycles of stable water isotopes in precipitation and streamflow. Thus, Fyw may be a useful metric in catchment inter-comparison studies that investigate landscape and hydro-climatic controls on streamflow generation. Here, we explore how Fyw varies with catchment characteristics and climatic forcing, using an extensive isotope data set from 22 small- to medium-sized (0.7–351 km2) Swiss catchments. We find that flow-weighting the tracer concentrations in streamwater resulted in roughly 26 % larger young water fractions compared to the corresponding unweighted values, reflecting the fact that young water fractions tend to be larger when catchments are wet and discharge is correspondingly higher. However, flow-weighted and unweighted young water fractions are strongly correlated with each other among the catchments. They also correlate with terrain, soil, and land-use indices, as well as with mean precipitation and measures of hydrologic response. Within individual catchments, young water fractions increase with discharge, indicating an increase in the proportional contribution of faster flow paths at higher flows. We present a new method to quantify the discharge sensitivity of Fyw, which we estimate as the linear slope of the relationship between the young water fraction and flow. Among the 22 catchments, discharge sensitivities of Fyw are highly variable and only weakly correlated with Fyw itself, implying that these two measures reflect catchment behaviour differently. Based on strong correlations between the discharge sensitivity of Fyw and several catchment characteristics, we suggest that low discharge sensitivities imply greater persistence in the proportions of fast and slow runoff flow paths as catchment wetness changes. In contrast, high discharge sensitivities imply the activation of different dominant flow paths during precipitation events, such as when subsurface water tables rise into more permeable layers and/or the river network expands further into the landscape.
- Article
(8159 KB) - Full-text XML
-
Supplement
(680 KB) - BibTeX
- EndNote
Naturally occurring variations in stable water isotopes (δ18O, δ2H) or chemically passive solutes (e.g. chloride) are commonly used in catchment studies to track the flow of water and to gain insight into catchment storage and mixing behaviour (Buttle, 1994; Kendall and McDonnell, 1998; Klaus and McDonnell, 2013). Many catchment studies use these tracers to estimate time-averaged transit time distributions, to characterize the heterogeneity of flow pathways, and to estimate mobile catchment storage (e.g. Benettin et al., 2015; Birkel et al., 2011; Hrachowitz et al., 2009; Staudinger et al., 2017). Transit time distributions are often inferred from conservative tracers using lumped-parameter models (McGuire and McDonnell, 2006). Because the mean transit time expresses the ratio between mobile catchment storage and the average flow rate, it is widely used in catchment inter-comparison studies (e.g. Hrachowitz et al., 2009; McGuire et al., 2005; Staudinger et al., 2017). However, estimates of mean transit time can be biased and unreliable, especially for spatially heterogeneous catchments (Kirchner, 2016b; Seeger and Weiler, 2014). Instead, the young water fraction Fyw – i.e. the average fraction of streamflow that is younger than a specified threshold age – has recently been proposed as a more reliable measure of water age in heterogeneous catchments (Kirchner, 2016a, b). Young water fractions with a threshold age of roughly 2–3 months can be estimated directly from the amplitude ratio of the seasonal cycles in stable water isotopes in precipitation and streamwater.
The amplitudes of the seasonal isotopic cycles in precipitation and streamwater can be estimated directly from the isotope measurements themselves, or by volume-weighting these measurements by the corresponding precipitation or discharge rates. Precipitation isotopes should generally be volume-weighted to prevent small precipitation events, potentially with anomalous isotope values, from substantially influencing the calculated seasonal precipitation isotope cycle. Streamwater isotope values can also be flow-weighted, using stream discharges as weights. Higher streamflows should typically correspond to larger young water fractions, for the simple reason that flow peaks typically follow intense rainfall and contain more recent precipitation than base flows (e.g. Kirchner, 2016b; von Freyberg et al., 2017). Hence, the flow-weighted average young water fraction (here denoted ) is expected to be higher than the unweighted average young water fraction (Fyw). Both Fyw and are calculated over periods of a year or longer, and represent the average catchment behaviour over that time. In calculating the unweighted Fyw, each unit of time counts equally, and benchmark tests using a nonstationary lumped catchment model confirm that the calculated Fyw should accurately reflect the time-averaged fraction of young water in discharge (Kirchner, 2016b). By contrast, in calculating the flow-weighted , each unit of flow counts equally, and benchmark tests confirm that the calculated reflects the cumulative volume of young water, as a fraction of the cumulative volume of discharge, over the corresponding period (Kirchner, 2016b). Although and Fyw have previously been compared in benchmark tests, a systematic evaluation based on tracer data from natural catchments has not yet been carried out.
At sites where precipitation isotopes are not measured directly, catchment isotopic inputs can be estimated from nearby long-term monitoring stations using various spatial interpolation methods. These interpolation methods differ in their assumptions about temperature- and elevation-dependent isotope fractionation effects, and their treatment of seasonal snowpack storage. Based on a global database of δ18O in precipitation, Jasechko et al. (2016) calculated the seasonal cycle amplitudes and their standard errors for each station and interpolated them to generate a global grid of the seasonal cycle amplitudes. These interpolated coefficients were volume-weighted by the spatial pattern of precipitation over each catchment. An alternative approach (Allen et al., 2018; see Supplement) builds on the Jasechko et al. (2016) method with an additional step that accounts for the residuals of the observations from the fitted seasonal cycles. To generate a high-resolution precipitation isotope map for Switzerland, Seeger and Weiler (2014) interpolated δ18O in monthly precipitation from long-term monitoring stations in central Europe, using an elevation-gradient approach. They combined their interpolation method with an energy-balance-based snow model to estimate the liquid input to the soil surface at monthly temporal resolution. The latter two interpolation methods have been rigorously tested with real-world isotope measurements, and thus may be particularly useful for estimating young water fractions in catchments where no long-term precipitation isotope measurements exist.
Another analytical decision that affects the interpretation of and Fyw relates to whether snowpack storage is considered to be part of catchment storage, or not. If one measures precipitation to the snow surface as the catchment input, then snowpack accumulation and melt are implicitly included in catchment storage (e.g. Staudinger et al., 2017). In this case, comparisons of seasonal cycles in precipitation and streamflow should reflect the young water fraction resulting from the combination of snowpack and subsurface storage. Alternatively, if one uses precipitation and snowmelt arriving at the soil surface as the catchment input (for example, with melt pan lysimeters, or modelled snowpack outflows), then snowpack accumulation and melt are implicitly excluded from catchment storage. In this case, comparisons of seasonal cycles in streamflow and sub-snowpack catchment input should reflect the young water fraction resulting from subsurface storage alone. Because the total catchment storage in the first case (including snowpack storage) is larger than the subsurface storage alone, the resulting young water fractions are expected to be smaller. Previous studies that estimated young water fractions in snow-dominated watersheds (Jasechko et al., 2016; Song et al., 2017) did not differentiate between these two concepts of catchment storage and simply used incoming precipitation in the young water fraction calculations, thus implicitly considering snowpack storage as part of catchment storage (as in the first case outlined above). This approach is practical in view of the challenges of measuring or modelling snowmelt and its isotopic composition. However, it is still unclear whether, in cases where snowmelt can be modelled or measured, explicitly considering snowmelt as a catchment input would significantly alter young water fraction estimates.
Because the young water fraction can be estimated from sparse and irregular tracer data, it has been suggested as a useful metric for catchment inter-comparison studies (Kirchner, 2016a). To date, however, most catchment inter-comparison studies have investigated controls on mean transit times instead. Mean transit times have been variably found to be correlated with (for example) flow path lengths and gradients (McGuire et al., 2005), drainage density (Soulsby et al., 2010), the areal fraction of hydrologically responsive soils (Tetzlaff et al., 2009), bedrock permeability (Hale and McDonnell, 2016), or combinations of multiple factors (Hrachowitz et al., 2009; Seeger and Weiler, 2014). So far, only a few catchment inter-comparison studies have used young water fractions (Song et al., 2017; Stockinger et al., 2016; Jasechko et al., 2016). A global analysis of 254 watersheds, revealed large spatial variability in young streamflow, which correlated inversely with average topographic gradients and water table depths (Jasechko et al., 2016). Jasechko et al. (2016) hypothesized that steeper landscapes are associated with more pervasive rock fracturing, deeper infiltration, and reduced shallow lateral flow, all of which would reduce the young water fraction in steep terrain. However, the correlation between topographic steepness and young water fractions was highly scattered, indicating that other factors are also involved. Jasechko et al.'s (2016) study sites were mostly larger than 1000 km2 (25th percentile 1753 km2, median 10 800 km2) and thus were probably affected by a complex interplay of landscape characteristics, climatic variability, and human impacts. Identifying landscape and climatic drivers that potentially control catchment storage behaviour may be easier in small- to medium-sized catchments with near-natural streamflow regimes (Holko et al., 2015).
In the present study, we use seasonal cycles in δ18O to estimate young water fractions for 22 sites in Switzerland with catchment areas between 0.7 and 351 km2. In a first step, we evaluate how choices of methodology affect the young water fraction estimates, with emphasis on (i) the spatial interpolation method for precipitation isotopes, (ii) the conceptual representation of snow storage, and (iii) flow-weighting the streamwater isotope data. Because the 22 study catchments cover a wide range of landscape and hydro-climatic characteristics, in the second part of this study, we test for correlations between the young water fraction and a wide range of landscape and hydro-climatic indices. Finally, we present a method for estimating the linear dependence of the young water fraction on the streamflow regime and propose that the slope of this relationship may be a diagnostic indicator of streamflow generation processes.
The isotopic composition of precipitation follows a seasonal cycle (Feng et al., 2009). The damping and phase shift of this seasonal cycle as it is transmitted through catchments (Fig. 1) can be used to infer timescales of catchment storage and transport (e.g. DeWalle et al., 1997; Soulsby et al., 2006). Sine-wave fitting can quantify the amplitude ratio AS∕AP and phase shift φS − φP between the seasonal isotope cycles in precipitation and streamflow (the indices P and S refer to precipitation and streamwater, respectively). The seasonal isotope cycles in precipitation and streamwater can be described by:
and
In Eqs. (1) and (2), A is the amplitude (‰), φ is the phase of the seasonal cycle (in radians, with 2 π rad equalling 1 year), t is the time (decimal years), f is the frequency (yr−1), and k (‰) is a constant describing the vertical offset of the isotope signal.
If one assumes that the transit times of water through the catchment follow a particular transit time distribution, the mean transit time can be calculated as a function of the amplitude ratio AS∕AP. However, mean transit times inferred from seasonal tracer cycles in runoff from heterogeneous catchments are potentially subject to severe aggregation bias (Kirchner, 2016a). Alternatively, the amplitude ratio AS∕AP can be used to estimate the fraction of water younger than a specified threshold age. Compared to the mean transit time, this “young water fraction” (Fyw) is markedly less vulnerable to aggregation bias, and less sensitive to the assumed shape of the catchment transit time distribution (Kirchner, 2016a, b). For a wide range of transit time distributions, the young water threshold age is approximately 2.3 ± 0.8 months (Kirchner, 2016a).
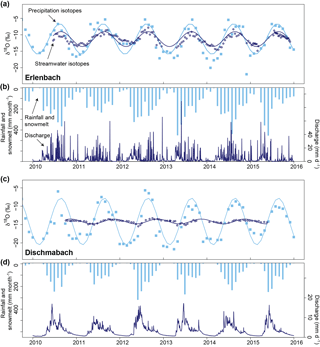
Figure 1Hydrologic and isotopic seasonality of precipitation and streamflow for the Erlenbach and Dischmabach catchments. Precipitation isotopes were interpolated with the method of Seeger and Weiler (2014). Sinusoidal cycles were fitted to the isotope data using iteratively re-weighted least squares regression. The seasonal cycles of the streamwater isotopes exhibit damping and phase shifts relative to the precipitation isotopic cycles. Stronger damping of the seasonal isotope cycle, implying a smaller fraction of young water in streamflow, can be observed in the Dischmabach catchment.
We can estimate the amplitudes AS and AP of the seasonal isotope cycles in Eqs. (1) and (2) by using multiple linear regression to obtain the coefficients a and b in
and
The amplitudes AS and AP are then determined by
and
Following Kirchner (2016a), we calculate young water fractions as the amplitude ratio AS∕AP. We estimate the coefficients aS, bS, aP, and bP by fitting Eqs. (3) and (4) using iteratively re-weighted least squares (IRLS), a robust estimation method that minimizes the influence of any potential outliers (an R script with our IRLS code is provided in the Supplement). In estimating aP and bP, we volume-weight Eq. (3) to avoid giving undue leverage to low-precipitation periods. To calculate the unweighted young water fraction Fyw, we estimate aS and bS from Eq. (4) using unweighted IRLS. For the flow-weighted young water fraction (), we estimate aS and bS from Eq. (4) using discharge-weighted IRLS (see the R script provided in the Supplement). Uncertainties in the calculated unweighted and flow-weighted young water fractions are expressed as standard errors (SEs) and are estimated using Gaussian error propagation.
The 22 study catchments cover areas between 0.7 and 351 km2 and have mean elevations between 472 and 2369 m a.s.l. (Table 1). Most of the sites are located in the Swiss Plateau and in the northern Alps, where the geology is characterized by sedimentary rocks (limestones, sandstones, marls, marly shales, conglomerates, breccias) and unconsolidated sediments (clay, silts, sands). In the southern Alps, two high-elevation catchments (Dischmabach and Riale di Calneggia) are predominantly underlain by metamorphic rock (mica schist, gneiss), and Ova da Cluozza is the only study catchment underlain by dolomite (Fig. 2a and b).
Table 1General properties of the 22 study catchments and streamwater isotope time series.
* Based on interpolated data from PREVAH and the time period January 2000–December 2015.
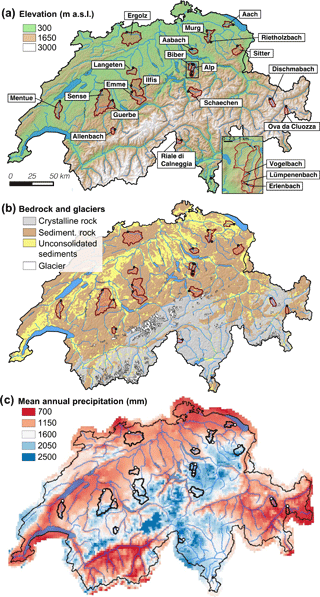
Figure 2Locations of the 22 study catchments in Switzerland (a), bedrock geology (b), and mean annual precipitation based on the observation period 1991–2010 (c). The expanded panel in (a) shows the sub-catchments of the Alp basin.
Land use at lower elevations (400–800 m) is predominantly agriculture, while grassland and forests can be found at elevations up to around 1400 m. Much of the area above 1700 m is characterized by grasses, shrubs, and sparse vegetation. At two high-elevation sites, Dischmabach and Ova da Cluozza, up to ∼ 2 % of the drainage area is covered by glaciers. At all sites, the human influence on river discharge is small, resulting in near-natural streamflow regimes.
Switzerland is characterized by a humid to temperate continental climate, with the Alps creating climatically distinct subregions. The wettest regions can be found in the northern pre-Alps and Alps, as well as in the canton of Ticino south of the Alps. The driest regions are located in inner Alpine valleys in the cantons of Valais and Grisons (Fig. 2c). Average annual precipitation rates for the 22 catchments range from 887 to 1853 mm based on observations from 2000 to 2015 (Table 1). To differentiate between the hydro-climatic regimes of the catchments, we grouped them into three classes (snow-dominated, rainfall-dominated, and hybrid) proposed by Staudinger et al. (2017). Precipitation is distributed more-or-less evenly throughout the year, although peak inputs to the soil surface (melt and precipitation) are shifted towards spring and summer in all snow-dominated sites and some hybrid sites.
3.1 Hydro-climatic data
Daily discharge data for 18 of the 22 sites were provided by the Swiss Federal Office for the Environment. Discharge measurements for the Aabach catchment were made available by the Office for Waste, Water, Energy and Air (WWEA) of the canton of Zurich. Discharge data for the Erlenbach, Vogelbach, and Lümpenenbach catchments were provided by the Swiss Federal Institute for Forest, Snow and Landscape Research (WSL), Birmensdorf, Switzerland.
Meteorological data for each site and each 100 m elevation band were interpolated from measurements taken by the national meteorological service of Switzerland (MeteoSwiss), using the PREVAH (Precipitation-Runoff-EVApotranspiration HRU) model (Viviroli et al., 2009). Mean precipitation for each 100 m elevation band was aggregated to obtain area-weighted catchment average values.
3.2 Catchment properties
The average hydro-climatic properties at the sites were described by various indices, such as mean monthly values of discharge and precipitation Q, as well as mean daily precipitation intensity . To quantify the variability of the flow regimes, we determined the average coefficient of variation of daily discharge (CVQ) and the quick-flow index (QFI). The QFI is the average ratio between (Q − Qbf) and Q, where Q is daily discharge and Qbf is daily baseflow; Qbf was calculated with the “BaseflowSeparation” function in the EcoHydRology package (version 0.4.12) in R using a recursive digital filter parameter of 0.925, as recommended by Nathan and McMahon (1990). All of these hydro-climatic indices were calculated for each site and for the duration of the site-specific streamwater isotope sampling campaigns, which varied between approximately 1 and 5 years (Table 1).
The seasonal variability of monthly precipitation for the years 2000–2015 was expressed through the amplitude and the phase shift of a fitted sinusoidal function (Berghuijs et al., 2014):
where P is the precipitation volume (mm month−1), is the average of P (mm month−1), Aprecip is the seasonal amplitude of precipitation (–), t is the time (months), τ is the duration of a full seasonal cycle (12 months), and φprecip is the phase (months). The phase describes the offset from the beginning of the seasonal cycle, which is defined here as 1 January. The parameters Aprecip and φprecip were obtained by non-linear fitting to the monthly precipitation data using Newton's method. Strong precipitation seasonality would be expressed in a high Aprecip value.
The hydro-climatic indices are to some extent redundant with one another. Unsurprisingly, mean monthly discharge () and mean monthly precipitation () were significantly correlated with each other across the 22 sites. Furthermore, was significantly correlated with the seasonality of precipitation (Aprecip), and the QFI was significantly correlated with the coefficient of variation of daily discharge (CVQ) (Table 4).
To quantify the geomorphological characteristics of the study catchments, we used terrain indices (median flow path length L, median flow gradient G, the ratio L∕G, and median topographic wetness index – TWI) which were calculated previously by Seeger and Weiler (2014) for all 22 study sites using a digital elevation model with 25 m spatial resolution. The indices L∕G and TWI were previously applied in numerous catchment inter-comparison studies, e.g. Hrachowitz et al. (2009), McGuire et al. (2005), and Tetzlaff et al. (2009). In addition, we calculated the drainage density DD (the total channel length divided by the catchment area) based on the official river network from the topographical landscape model of Switzerland (swissTLM3D, ©2017 swisstopo; resolution 8 m or better).
Hydrologic soil properties and vegetation cover information were extracted from geospatial data provided by the Swiss Federal Office for Agriculture (BLW, 2012) and the Swiss Federal Statistical Office (BFS, 2004), respectively. The data product “land suitability” uses six soil properties – soil depth, large particle fraction, water storage capacity, nutrient storage capacity, permeability, and soil wetness index – to generate a map of 144 different soil classes. Each soil property is ranked from 0 (very low) to 5 or 6 (very high). For our analysis, we calculated the areal fractions of aggregated soil properties that are usually associated with fast runoff processes, i.e. low water storage capacity (ranks 1–3), low permeability (rank 1–3), and high soil wetness index (i.e. saturated soils, ranks 4–5). From the data product “forest diversity” we extracted the fraction of forested area for each catchment.
The hydrogeological properties of the study sites were obtained from the official geotechnical map of Switzerland (1 : 200 000, ©2017 swisstopo). We extracted the areal fractions of low, intermediate, and high groundwater productivity for each catchment. Representative groundwater table depths could not be determined for all sites due to their complex small-scale topographic and geologic heterogeneity. The hydrologic soil properties, as well as the hydrogeological properties of the individual sites, are provided in the Supplement (Table S1).
Correlations between the catchments' young water fractions, hydro-climatic conditions, and landscape properties were assessed with the Spearman rank correlation coefficient ρ (Spearman, 1987). Following conventional practice, we consider correlations with p < 0.05 to be statistically significant.
3.3 Streamwater isotope data
Streamwater grab samples were collected approximately fortnightly at 21 sites between mid-2010 and mid-2011 or later (see Table 1 for exact dates). Oxygen isotope ratios (δ18O) were measured with a Picarro isotope analyser (Picarro Inc., Santa Clara, CA, USA) at the University of Freiburg, Germany, and are reported here as δ values relative to the VSMOW standard. For the Rietholzbach catchment, fortnightly streamwater δ18O data were provided by the Institute for Atmospheric and Climate Science at ETH Zurich.
3.4 Precipitation isotope data
Values of δ18O in precipitation were not measured directly at the 22 study catchments. Instead, δ18O values from monthly cumulative precipitation samples were interpolated from long-term observations at nearby monitoring stations (the Swiss network for Observations of Isotopes in the Water Cycle – NAQUA-ISOT, the Global Network of Isotopes in Precipitation – GNIP, and the Austrian Network of Isotopes in Precipitation – ANIP). We used two different interpolation approaches that we summarize below: method 1 after Seeger and Weiler (2014) and method 2 similar to that of Allen et al. (2018). More detailed descriptions of both interpolation methods 1 and 2 can be found in Seeger and Weiler (2014) and in the Supplement, respectively.
In method 1, we adjusted a kriging interpolation of the available precipitation isotope values from 26 long-term monitoring stations for local differences in elevation. For this, we used the monthly average elevation gradient of δ18O in precipitation, estimated from three isotope monitoring stations in central Switzerland (Meiringen, Guttannen, and Grimsel, Fig. S1 in the Supplement) that cover a similar elevation range as the 22 study catchments. Method 1 can be extended using an energy-balance-based model to explicitly simulate the storage of winter precipitation in the snowpack. The energy-balance-based model uses PREVAH simulations of air temperature, wind speed, incoming shortwave radiation, and precipitation amount to predict the meltwater amounts and their average isotopic compositions for each 100 m elevation band (without considering isotopic fractionation of the snowpack and snowmelt).
In method 2, we fitted isotope data from 19 long-term monitoring stations to sine curves using least squares. We then constructed a multiple linear regression model to explain the best-fit sine parameters as functions of latitude, longitude, and elevation. These spatially varying sine parameters were used to construct interpolated seasonal cycle maps for all of Switzerland. These seasonal cycles were then adjusted using kriged interpolations of the monthly residuals of station measurements from their fitted seasonal patterns, to account for non-sinusoidal isotope dynamics. For both interpolation methods 1 and 2, monthly isotope values were mass-weighted based on the monthly elevation-dependent precipitation volumes obtained from the PREVAH model (Viviroli et al., 2009).
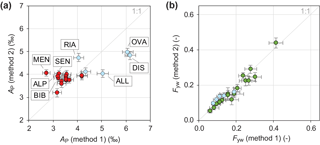
Figure 3(a) Comparison of flow-weighted seasonal amplitudes of precipitation δ18O cycles (AP) obtained with two different interpolation methods, method 1 (Seeger and Weiler, 2014) and method 2 (based on Allen et al., 2018; Supplement). Differences in AP between the two interpolation methods were significant for the catchments highlighted with their abbreviated names. The abbreviations for the study sites stand for Allenbach (ALL), Alp (ALP), Biber (BIB), Dischmabach (DIS), Mentue (MEN), Ova da Clouzza (OVA), Riale di Calneggia (RIA), and Sense (SEN). (b) Comparison of young water fractions derived from the two interpolation methods. High-elevation, snow-dominated catchments are marked in light blue colour. Error bars show ±1 SE.
4.1 Comparing two methods for spatial interpolation of δ18O in precipitation
Here, we apply two different methods 1 and 2 (Sect. 3.4) for interpolating monthly precipitation isotopes from nearby long-term monitoring stations and compare the resulting seasonal cycles of precipitation isotopes and their effects on the calculated young water fractions. In this comparison, method 1 is used without the snow module because method 2 does not allow for explicit simulation of snow accumulation and melt.
Figure 3a shows that the seasonal precipitation isotope cycle amplitudes (AP) obtained with both methods are similar for most catchments; the differences range from −1.34 ± 0.21 ‰ (±SE, Mentue) to 1.35 ± 0.29 ‰ (Dischmabach). Method 2 results in larger AP values for five sites (Alp, Biber, Mentue, Sense, and Riale di Caneggia), compared to the results of method 1 (Fig. 3a). However, smaller AP values are obtained with method 2 for three high-elevation sites: Allenbach, Dischmabach, and Ova de Cluozza. Overall, AP spanned a range of 1.77 ‰ with method 2, compared to a larger range of 3.47 ‰ with method 1. Nevertheless, for most sites the differences in AP between the two methods are small compared to the absolute values of AP, and thus the choice of the interpolation method only marginally affects the estimated young water fractions Fyw. For all sites, the absolute differences between the values of Fyw calculated with the two interpolation methods are below 0.06 and statistically insignificant (i.e. smaller than twice their pooled uncertainties, Fig. 3b).
A systematic test of both interpolation methods using on-site, long-term precipitation isotope measurements would go beyond the scope of this study. However, method 1 was tested with isotope measurements from six stations (Seeger and Weiler, 2014), and we evaluated the performance of method 2 as described in the Supplement. Results from the two methods are likely to differ because they make different assumptions about the changes in precipitation isotopic composition with elevation. For our objectives, however, it is helpful that these two different approaches yield different AP in several cases, because it allows us to show that this level of variability in AP has only minor effects on the calculated young water fractions. Our comparison thus demonstrates that both approaches for spatially interpolating δ18O in precipitation yield consistent young water fraction estimates for the 22 study catchments.
4.2 The effect of snow storage on the seasonal cycle amplitudes and phases of precipitation isotopes
At high-elevation sites with seasonally cold climates, precipitation (and its isotopic signature) will be stored temporarily in the snowpack in winter, and will be released during the melt season. Thus, significant volumes of isotopically depleted snow meltwater may reach the river system during spring and early summer, when the isotope signal of incoming precipitation is more enriched. As a result, the seasonal isotopic variation in water reaching the soil surface (rainwater and snowmelt) is likely to be smaller than the seasonal variation in precipitation alone.
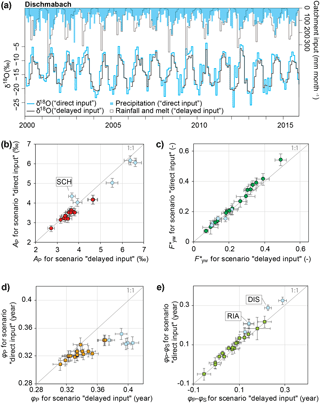
Figure 4(a) Time series of catchment input volumes and δ18O values (not volume-weighted) for the Dischmabach catchment, calculated using the interpolation method of Seeger and Weiler (2014), with and without modelling of snow accumulation and melt (“delayed input” and “direct input”, respectively). Panels (b) and (c) compare the seasonal amplitudes of the precipitation isotope cycles (volume-weighted), and the resulting flow-weighted young water fractions, with and without modelling of snow accumulation and melt. Panels (d) and (e) compare the phases of the seasonal precipitation isotope cycles, and the resulting phase shifts, with and without modelling of snow accumulation and melt. High-elevation, snowmelt-dominated sites are marked in light blue. The abbreviations for the study sites stand for Dischmabach (DIS), Riale di Calneggia (RIA), and Schaechen (SCH). Error bars show ±1 SE.
In order to investigate the effect of snow storage on the amplitudes and phases of precipitation isotope cycles, we applied method 1 with the snow module, so that the input to the soil surface, and its isotope signal, can be described by a mixture of rainwater and snowmelt (the “delayed input” scenario in Fig. 4). Alternatively, method 1 can also be applied without the snow module, i.e. by ignoring snowpack as a separate storage, such that the catchment input is taken directly from the incoming precipitation and its isotopic composition (the “direct input” scenario in Fig. 4). Figure 4a shows, as an example, the time series of input water flux and δ18O (not volume-weighted) at the Dischmabach catchment for both scenarios. The delayed release of depleted winter precipitation from the snowpack (“delayed input” scenario) results in a smaller seasonal amplitude of the input tracer signal. However, when this input tracer signal is volume-weighted, the fitted seasonal amplitudes (AP) are statistically indistinguishable between the “direct” and “delayed” input scenarios for 21 of the 22 sites (Fig. 4b). This result arises because the “delayed” input scenario gives very little weight to winter inputs in snow-dominated catchments (because snowmelt volumes during winter conditions are small), allowing the fitted cycles to deviate from the winter isotope values. The difference in AP for both scenarios is statistically significant only at the Schaechen catchment, which contains the highest-elevation snowpacks in our data set (elevation up to 3260 m a.s.l., Table S1). As a consequence, snowmelt at the Schaechen site is isotopically more depleted compared to the other, lower-elevation sites. For the hybrid and rain-dominated sites, the AP values are almost indistinguishable between the two scenarios, either because snowmelt occurs early in the season when rainwater and snowmelt have similar isotopic signatures (i.e. hybrid catchments), or because the contribution of snowmelt is small compared to that of rainfall (rain-dominated catchments). As a consequence, the young water fractions Fyw are virtually identical between the “direct input” and “delayed input” scenarios (Fig. 4c).
As can be seen in Fig. 4a, the delayed meltwater input shifts the seasonal isotope pattern toward later in the season. Thus the “delayed input” scenario results in later cycle phases (φP) compared to the “direct input” scenario (Fig. 4d), with statistically significant differences for the five high-elevation, snow-dominated sites and for four hybrid catchments (Erlenbach, Lümpenbach, Vogelbach, and Sitter). However, the “delayed input” scenario had a statistically significant effect on the phase shift between input and output (φS − φP) only at Dischmabach (where it altered the phase shift by 0.06 years) and Riale di Calneggia (where it altered the phase shift by 0.07 years; Fig. 4e). In the analysis presented below, we use interpolated precipitation isotope values obtained with method 1 that explicitly account for snowpack accumulation and melt (i.e. the “delayed input” scenario) in order to be consistent with previous studies where this data set has been used (Seeger and Weiler, 2014; Staudinger et al., 2017).
4.3 Comparing unweighted and flow-weighted young water fractions
We use the isotope and discharge data sets of the 22 catchments to estimate young water fractions from the ratios of the seasonal cycle amplitudes AS and AP, with and without discharge-weighting ( and Fyw, respectively). Figure 5a shows that flow-weighting the streamwater isotope values results in a roughly 25 % increase in the fitted seasonal streamwater isotope cycle amplitudes AS, relative to the unweighted AS values for the same sites. Statistically significant differences between unweighted and flow-weighted values of AS were found for Dischmabach, Emme, Mentue, Rietholzbach, and Sense, as well as Alp, Erlenbach, Lümpenenbach, Vogelbach, and Biber (which are all located nearby one another and share similar catchment characteristics). Perhaps unsurprisingly, the effect of flow-weighting on AS is largest in catchments with highly variable flow regimes, i.e. at sites with relatively large coefficients of variation of daily discharge (CVQ) and QFIs (Table 2). In such catchments, robust estimation of the flow-weighted may require a smart sampling strategy that captures a representative range of hydrologic conditions.
The flow-weighted values range from 0.07 ± 0.01 to 0.49 ± 0.03 (±SE), whereas the unweighted Fyw values range from 0.06 ± 0.01 to 0.37 ± 0.03. Thus, flow-weighting the streamwater isotope values yields young water fractions () that are around 26 % larger than those calculated from unweighted streamwater isotope values (Fyw; Fig. 5b, Table 3), because high flows generally contain more young water than base flows. The average values of and Fyw are 0.22 ± 0.02 and 0.17 ± 0.02, respectively, meaning that approximately one-fifth of total discharge was younger than roughly 2.3 ± 0.8 months (assuming that the catchment transit times can be described by gamma distributions with shape factors α ranging from 0.3 to 2; Kirchner, 2016a). Our Fyw results are within the range of young water fractions reported for rivers in mountainous regions in North America and central Europe by Jasechko et al. (2016).

Figure 5Panel (a) compares the seasonal amplitudes of streamwater isotope cycles (AS) with and without flow weighting. High-elevation, snowmelt-dominated sites are marked in light blue. Panel (b) compares flow-weighted young water fractions with unweighted young water fractions (Fyw). Error bars show ±1 SE. Unweighted young water fractions are roughly 26 % smaller than flow-weighted young water fractions across these catchments.
By examining how the catchments' young water fractions correlate with their landscape and hydro-climatic characteristics, we aim to identify dominant controls on their hydrological behaviour. Below, we present our results for flow-weighted young water fractions (); however, the unweighted young water fractions (Fyw) yield very similar results, as both values are significantly correlated with each other (ρ = 0.9, p < 0.001; Table 4).
Table 2Hydro-climatic and topographic indices, as well as soil properties of the 22 study catchments.
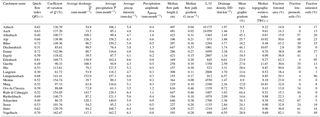
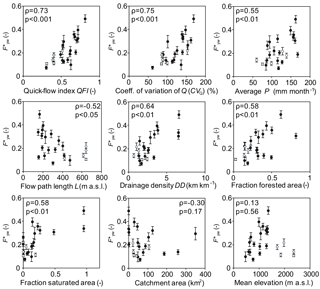
Figure 6Scatter plots showing how young water fractions correlate with climatic and landscape indices. High-elevation, snowmelt-dominated sites are marked in light blue. Error bars show ±1 SE. Spearman rank correlation coefficients (ρ) and corresponding p values are provided in the individual figures.
Table 4 and Fig. 6 show that young water fractions exhibit statistically significant positive correlations with five hydro-climatic indices: mean monthly discharge (), mean monthly precipitation (), mean daily precipitation intensity (), coefficient of variation of daily discharge (CVQ), and QFI. These correlations suggest that young water fractions tend to be highest in humid catchments where prompt runoff response is facilitated by fast flow paths and/or high-intensity precipitation events. was also significantly correlated with high values of drainage density (DD) and low values of flow path length (L) (Table 4). There was also a significant negative correlation with the ratio of the flow path length to gradient (L∕G), but as there is nearly zero correlation with G itself, the correlation with L∕G apparently arises through L alone. Drainage density is inversely proportional to median flow path length, so the strong positive correlation of with DD and negative correlation with L can be viewed as two sides of the same coin. All else equal, high values of DD, and thus small values of L, facilitate faster runoff, which is directly linked to higher values of CVQ and QFI.
A statistically significant inverse correlation (ρ = −0.36, p < 0.0001) between Fyw and the logarithm of the topographic gradient was found by Jasechko et al. (2016) for 254 sites across Europe and North America, with the surprising implication that steeper catchments have less (not more) young streamflow. Among our individual catchments, however, we find no correlation between Fyw (or ) and topographic gradient. This may be partly explained by the lack of low-gradient catchments among our study sites; our gradients span a range of 0.02–0.64 compared to ∼ 0.0007–0.11 in Jasechko et al. (2016), and the correlation that they observe appears to be largely driven by sites with gradients less than roughly 0.01. Nevertheless, our data set fits within the global pattern found by Jasechko et al. (2016), and the median Fyw of our 22 mostly high-gradient study catchments (0.16, 95 % confidence interval 0.10–0.21) is smaller than the global median (0.21, 95 % confidence interval 0.19–0.24) consistent with the gradient-dependence hypothesized by Jasechko et al. (2016).
Table 3Values ± SE (standard errors) of flow-weighted seasonal amplitude coefficients of precipitation isotopes (AP), unweighted and flow-weighted seasonal amplitude coefficients of streamwater isotopes (AS), unweighted and flow-weighted young water fractions, and the discharge sensitivity of the young water fraction (estimated as the linear slope of the Q–Fyw relationship; see Sect. 6).
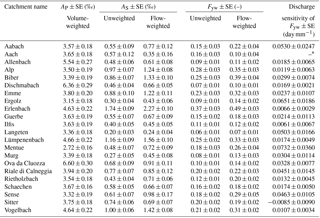
* The catchment Aach was omitted from the analysis because its isotope data set contained only two data points during high-flow conditions.
Some studies have identified catchment area as a major control on mean transit times (e.g. DeWalle et al., 1997; Soulsby et al., 2000), however, the inverse correlation of and Fyw with catchment area only becomes significant (ρ = −0.49, p < 0.05) when the five high-elevation, snow-dominated sites are omitted from the analysis (Fig. 6). The young water fractions of the remaining 17 sites were also strongly correlated with mean catchment elevation (ρ = 0.65, p < 0.005, Fig. 6), which in turn is a major control on other hydro-climatic indices (, ) and topographic indices (DD, G, L, L∕G, and TWI).
Across the 22 catchments, is positively correlated with the areal fraction of saturated soils (ρ = 0.58, p < 0.01) and low-permeability soils (ρ = 0.52, p < 0.05). These relationships remain significant when the snow-dominated sites are omitted from the analysis. A strong positive relationship with can be expected because saturated soils and low-permeability soils are often associated with overland flow and/or fast subsurface flow mechanisms triggered by exceedance of soil water storage thresholds (saturation excess; Dunne and Black, 1970) or precipitation intensity (infiltration excess; Horton, 1933). Particularly high fractions of saturated soils occur at three neighbouring catchments (Erlenbach, Lümpenenbach and Vogelbach) that are characterized by shallow gleysols (Feyen et al., 1996; Fischer et al., 2015). Together with the nearby Biber catchment, these four sites exhibit the largest young water fractions in our data set. No correlation was evident between and the fraction of soils with low water storage capacity, likely due to the strong influence of six sites where this fraction was zero.
is not significantly correlated with the areal fractions mapped as having high, intermediate, or low groundwater productivity, here used as a proxy for the catchments' hydrogeologic properties. This result is perhaps unsurprising; most groundwater is probably older than the threshold age that defines young water, so the young water fraction will not be sensitive to how much older the groundwater is. Instead, the fraction of young water should primarily reflect mechanisms that control flow processes and routing near the land surface (shallow groundwater, soil water, overland flow) rather than groundwater flow in deep aquifers where flow velocities can be several orders of magnitude slower.
Table 4Spearman rank correlation coefficients relating the flow-weighted () and unweighted (Fyw) young water fractions, and the discharge sensitivity of Fyw, to selected hydro-climatic indices and landscape properties of the 22 Swiss catchments. The corresponding p values are indicated by regular font in grey fields (p < 0.05), bold font in grey fields (p < 0.01), as well as italic and underlined font in grey fields (p < 0.001); fields without grey shading indicate p > 0.05.


Figure 7Variation in unweighted young water fractions with flow regime (log-transformed) for the nine Swiss catchments that have sufficiently long time series of streamwater isotope measurements. Error bars show ±1 SE. The young water fraction increases with discharge differently at different sites, suggesting different degrees of activation of fast flow paths at high flows.
Across our study catchments, the young water fraction is strongly correlated with the areal fraction of forest (ρ = 0.58, p < 0.01; Tables 1 and 4). Excluding the snow-dominated sites from the analysis slightly weakens this relationship although it remains statistically significant (ρ = 0.51, p < 0.05). One would normally expect tree roots to increase soil permeability, resulting in greater infiltration and groundwater recharge (Brantley et al., 2017). However, on steep forested slopes, abundant lateral preferential flow pathways (e.g. macropores) may facilitate rapid transport of water (Whipkey, 1965). Thus, the correlation we observe may be artefactual, since across our sites, forest cover is also correlated with higher drainage densities and shorter mean flow paths, as well as higher fractions of saturated and low-permeability soils, all of which can plausibly increase the young water fraction. More generally, among our 22 study sites, hydro-climatic characteristics are correlated with landscape properties, making it challenging to clearly identify individual controls on the young water fraction. Broadly, however, we can conclude that high young water fractions are generally associated with hydro-climatic factors (e.g. humid climate and high precipitation intensity) and landscape characteristics (e.g. low soil permeability and high drainage density) that facilitate fast streamflow responses.
5.1 Discharge sensitivity of the young water fraction as a diagnostic indicator of runoff generation processes
The catchment inter-comparison analysis presented in Sect. 5 suggests that wetter catchments, and those with shorter and faster flow paths, have larger young water fractions. In individual catchments, one would also expect young water fractions (and thus seasonal isotope cycles) to be variable in time, i.e. to be larger during periods of stronger precipitation forcing and wetter antecedent conditions, as shallower, faster flow paths become more dominant, and as the stream network extends farther into the landscape, shortening the average path length of subsurface flow (Godsey and Kirchner, 2014). In this section, we examine how young water fractions respond to changes in catchment wetness, as reflected in stream discharge.
5.2 Young water fractions of distinct flow regimes
Our expectation that the young water fraction should be higher under wetter conditions (and thus during higher stream discharges) is borne out by the observation that flow-weighted young water fractions are systematically higher than unweighted young water fractions (Sect. 4.3). We can visualize the relationship between Fyw and stream discharge (as a proxy for catchment wetness) by separating the streamwater isotope time series into different discharge ranges and calculating the seasonal isotope cycles and Fyw values individually for each of these flow regimes. These flow regimes comprise the 1st to 4th quartiles, as well as the upper 20 and 10 % of daily discharges at the day of sampling. For instance, from the 140 streamwater isotope samples at the Erlenbach site, each quartile of Q comprised 35 samples, while the upper 20 and 10 %, of daily discharges comprised 28 and 14 samples, respectively. In Fig. 7, we plot Fyw in relation to the median discharge values of the six flow regimes at nine of our study sites. These sites have the longest isotope time series in our data set, allowing us to estimate robust seasonal cycle coefficients AS for each individual flow regime. At our sites with shorter time series, sub-sampling individual flow regimes would result in highly uncertain AS estimates.
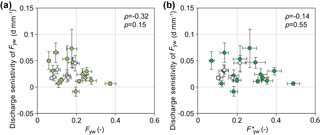
Figure 8Scatter plots of the unweighted and flow-weighted young water fractions versus the discharge sensitivity of Fyw calculated for 21 of the 22 Swiss catchments (no discharge sensitivity was calculated for the Aach catchment because only two isotope values existed for high-flow conditions). High-elevation, snowmelt-dominated sites are marked in light blue. Error bars show ±1 SE. There is no systematic relationship between the young water fractions and their discharge sensitivities.
The visual patterns shown in Fig. 7 are similar for catchments located close to each other, such as for Alp and Biber, or for Lümpenenbach, Vogelbach, and Erlenbach. However, young water fractions vary substantially among the sites in Fig. 7, with Fyw in the lowest flow regime ranging from 0.03 at Dischmabach to 0.29 at Erlenbach and Fyw in the highest flow regime ranging from 0.13 at Ilfis to 0.60 at Biber. Figure 7 suggests that the relationship between discharge and Fyw may be a diagnostic fingerprint linked to hydrological properties that control the storage and release of young water. However, the nine catchments shown in Fig. 7 are too small of a sample to draw any robust conclusions concerning how this fingerprint may vary with catchments' landscape characteristics and hydro-climatic conditions.
5.3 Estimating the discharge sensitivity of Fyw and linking it to catchments' landscape and hydro-climatic characteristics
As a first-order estimate of the sensitivity of Fyw to discharge across all 22 study catchments, we calculated the linear slope of the relationship between Q and Fyw, using a method that does not require breaking the streamwater isotope time series into separate flow regimes (and thus has more modest data requirements than plots like Fig. 7). Instead of fitting a linear slope to the few data points shown in Fig. 7, we estimated the linear slope of the Q–Fyw relationship directly from the tracer time series cS(t) and cP(t). For each site, we assume that the seasonal amplitude of precipitation isotopes (AP) is independent of Q, leaving the seasonal amplitude of streamwater isotopes AS as the only flow-rate-dependent variable. If AS varies with discharge but AP does not, then the young water fraction Fyw varies with Q as follows:
If we approximate AS as a linear function of Q,
we can estimate the linear slope (mS) and the intercept (nS) through nonlinear fitting (analytic Gauss–Newton algorithm) by replacing AS in Eq. (2) with AS(Q) from Eq. (6), yielding the following:
In Eq. (8), φS is the phase of the seasonal streamwater isotope cycle (rad), t is the time (decimal year), f is the frequency (yr−1), and kS (‰) is a constant describing the vertical offset of the streamwater isotope signal. For the sake of simplicity, Eq. (8) assumes that the amplitude of the seasonal cycle varies with Q but the phase φS does not. Numerical experiments (e.g. Fig. 8 in Kirchner, 2016b) suggest that the change in streamwater isotope cycle phase φS between high and low flows should have only a minor influence on the estimate of the parameters in Eq. (8), because the change in φS can only be large when the cycle is strongly damped (i.e. during low-flow conditions), and the phase of such a strongly damped cycle will have little effect on the fit to the data.
Combining Eqs. (6) and (7) yields
and thus, the linear slope of the dependence of Fyw on Q can be approximated as mS∕AP, which has units of Q−1. The uncertainty in this slope was estimated through Gaussian error propagation. Please note that Eq. (9) quantifies discharge sensitivity based on the linear slope of the relationship between Fyw and Q, whereas Fig. 7 shows how Fyw varies with log(Q) for different fractions of the discharge distribution. By replacing Q with log(Q) in Eqs. (6)–(9), one could easily determine the linear slope of the relationship between Fyw and log(Q) instead.
For convenience, we term this linear slope of the Q–Fyw relationship the “discharge sensitivity” of Fyw. Our use of this term should not be interpreted to mean that Fyw depends, in a mechanistic sense, on discharge per se. Instead, we use the term to indicate the statistical sensitivity of Fyw to discharge, where discharge is a proxy indicator of catchment wetness conditions and hydro-climatic forcing. Catchments with high discharge sensitivity of Fyw (steep linear slope in Eq. 9) are ones in which the young water fraction varies greatly between low and high flows, suggesting that faster flow paths are more predominant in larger events. Conversely, catchments with low discharge sensitivity (shallower linear slopes in Eq. 9) are ones in which young water fractions are broadly similar between low and high flows, suggesting that the same predominant flow paths are activated in similar proportions in both large and small runoff events.
On average, we find that every 1 mm day−1 increase in discharge is associated with an increase of 0.0202 ± 0.0046 in Fyw. From this analysis, we excluded the Aach catchment because only two streamwater samples were collected during high-flow conditions, resulting in an unrealistic and highly uncertain value for mS. At the remaining 21 sites, the discharge sensitivities of Fyw range between zero (within error) at Ilfis and Sitter, and 0.0732 ± 0.0360 day mm−1 at Mentue. A similar analysis was carried out by Wilusz et al. (2017) for two neighbouring catchments in Plynlimon, Wales. For those two sites, Wilusz et al. (2017) combined a rainfall–runoff model with a rank storage selection (rSAS) transit time model and estimated an increase in Fyw of 0.031 to 0.040, respectively, with every 1 mm day−1 increase in average annual precipitation. Multiplying their “precipitation sensitivities of Fyw” by the site-specific runoff ratios (0.78 and 0.90) yields average discharge sensitivities of Fyw of 0.0242 and 0.0360 day mm−1, respectively, which are within the range of values we obtained for our 22 Swiss study sites. Even though the methods, tracers, and timescales Wilusz et al. used to estimate Fyw differed from ours, the similarity in the discharge sensitivities between their sites and ours suggests that this may be a robust and reproducible metric that could be useful in future catchment studies.
For our study catchments, there was no systematic relationship between the young water fraction (either Fyw or ) and the discharge sensitivity, indicating that they are different and largely independent measures of catchment behaviour (Figs. 8 and 9). The discharge sensitivity of Fyw is, however, strongly correlated to a range of landscape and hydro-climatic conditions, including (ρ = −0.64, see also Fig. 9b), (ρ = −0.56), (ρ = −0.61), DD (ρ = −0.59), L∕G (ρ = 0.75), L (ρ = 0.46), G (ρ = −0.46), TWI (ρ = 0.52), Aprecip (ρ = −0.44), and mean catchment elevation (ρ = 0.44). All of these correlations remain statistically significant (and many become stronger) when the snow-dominated sites are excluded from the analysis.
In contrast, calculating linear slopes between Fyw and log(Q), instead of Q, yields no significant correlations with any of the variables in Tables 2 or S1. It should be noted that calculations based on log(Q) will be more strongly influenced by small discharges, whereas calculations based on Q will be more strongly influenced by the upper tail of the Q distribution. Thus, since our primary focus is storm runoff generation, we interpret the discharge sensitivities of Fyw based on Q instead of log(Q).
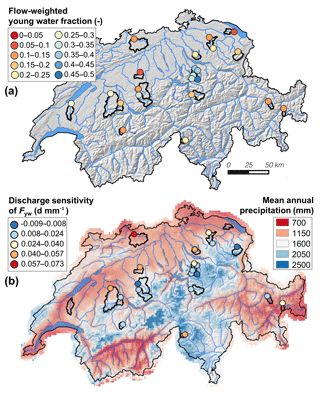
Figure 9(a) Flow-weighted young water fractions at the 22 Swiss study catchments; (b) discharge sensitivity of Fyw at the same sites (mean annual precipitation for the period 1991–2010 is shown for comparison).
Our results suggest that catchments with low discharge sensitivity of Fyw are characterized by high elevations, dense river networks (high DD, low L∕G) and/or generally humid conditions (high ). These catchment properties are generally associated with predominantly shallow runoff flow paths during both large and small precipitation events, such that the fraction of young water remains relatively high under widely varying flow regimes. In contrast, in catchments characterized by lower drainage density and less humid conditions, larger or higher-intensity storms are likely to strongly alter the proportions of different dominant flow paths, leading to bigger variations in Fyw (i.e. higher discharge sensitivity). For example, the dynamic extension of the stream network (e.g. Godsey and Kirchner, 2014; Jensen et al., 2017) and/or the increase in hydrologic connectivity between the stream network and the surrounding landscape (e.g. Detty and McGuire, 2010; Phillips et al., 2011; von Freyberg et al., 2015) should more strongly influence the relative proportion of young streamflow in catchments where drainage density is not already high. Likewise, the activation of shallow flow paths during larger storm events will have a bigger influence on Fyw in drier catchments than in wetter ones, where shallow flow paths are likely to be activated during both large and small events.
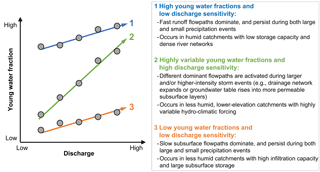
Figure 10Conceptual description of the mechanistic relationship between young water fractions and discharge, which is used here as a proxy for catchment wetness and hydro-climatic forcing. The three colours of the arrows represent three individual hypothetical catchments.
Interestingly, although Fyw and its discharge sensitivity are not significantly correlated with each other, they are often correlated with catchment characteristics in opposite ways (Table 4). For example, DD, , , , QFI, and CVQ exhibit positive correlations with Fyw but also exhibit negative correlations with the discharge sensitivity of Fyw. In catchments with dense river networks and/or generally humid climates, fast runoff flow paths will dominate (and thus Fyw and will be high). These same conditions should also make fast runoff flow paths more persistent, with the result that the young water fraction will not be strongly dependent on catchment wetness conditions or hydro-climatic forcing (and thus discharge sensitivity will be low).
5.4 A conceptual model of the mechanistic relationship between young water fractions and discharge
Figure 10 presents a conceptual summary of the relationships between the young water fraction, its discharge sensitivity, and landscape and hydro-climatic characteristics that control streamflow generation. We suggest that the general trend of the Q–Fyw relationship is positive because high-flow periods during precipitation events are likely to contain larger fractions of young water travelling by quick flow paths, while low-flow conditions are primarily sustained by older groundwater. In Fig. 10, the steepness of the linear slope expresses how extensively fast flow paths are activated during high flows. In theory, a linear slope of zero (i.e. Fyw insensitive to discharge) would represent strictly linear rainfall–runoff behaviour with a constant mixing fraction of young and old water. In natural systems, however, the relative proportions of streamflow generation mechanisms are likely to vary between high and low flows, making Fyw sensitive to discharge. From our analyses in Sect. 6.1. and 6.2, we find that low discharge sensitivities of Fyw can occur at sites with either high or low young water fractions (cases 1 and 3, respectively, in Fig. 10; e.g. Erlenbach and Ilfis, respectively, in Fig. 7). Case 1 might be found in humid catchments with frequent precipitation, low storage capacity, and dense river networks, where shallow runoff flow paths dominate both during and between events (e.g. triggered by saturation excess). Case 3 is more likely to occur in catchments with high infiltration capacity and large subsurface storage, where slow subsurface flow paths dominate both during events and between them, leading to consistently low young water fractions. A steep linear slope (case 2 in Fig. 10; e.g. Alp, Biber or Murg in Fig. 7) is likely to occur in catchments where the relative contributions of fast and slow flow paths vary dramatically in response to hydro-climatic forcing or antecedent wetness conditions, for example through drainage network expansion, or shifts in hydrological connectivity due to groundwater tables rising into more permeable layers.
The hydrological concepts presented in Fig. 10 are based on the young water fraction analysis for 21 Swiss catchments that share several landscape and hydro-climatic characteristics, such as similar vegetation cover, relatively humid climate, and (partly) mountainous terrain. Hence, we must be cautious about extending this conceptual model to regions characterized by (semi-)arid or arctic climates, very different vegetation cover or predominantly flat terrain. In addition, linking young water fractions to catchment wetness conditions and hydro-climatic forcing may be difficult in catchments with streamflow regimes that are discontinuous or strongly affected by lakes, water management (e.g. groundwater pumping, artificial groundwater recharge, irrigation, or water diversion) or land-use change (e.g. urban development, soil degradation, or forest clear cutting). Nevertheless, long-term tracer data sets from other catchments could be used to expand our analysis beyond the Swiss study sites and to test the transferability of the conceptual model presented in Fig. 10.
The fraction of streamflow younger than roughly 2–3 months has recently been proposed as a robust measure of water age which can be estimated directly from the seasonal cycles of stable water isotopes in precipitation and streamflow (Kirchner, 2016a, b). Here, we have leveraged an extensive isotope data set from 22 small- to medium-sized Swiss catchments to explore how the young water fraction (Fyw) varies with catchment characteristics and climatic forcing.
Catchment inter-comparison studies require application of consistent procedures across sites, so we quantified how choices of methodology may affect estimates of Fyw. Across the 22 sites, Fyw values were not particularly sensitive to the spatial interpolation methods used to estimate precipitation isotope signatures (Sect. 4.1), or sensitive to whether one accounts for snow accumulation and melt in estimating isotopic inputs to the catchment (Sect. 4.2). Flow-weighting the streamwater isotope measurements, however, yielded flow-weighted young water fractions () that were roughly 26 % larger than their unweighted counterparts (Fyw; Sect. 4.3, Fig. 5). This result is not surprising, because flow peaks typically follow intense rainfall and thus should contain more recent precipitation than base flows. Here we quantify, for the first time, how flow-weighting affects young water fractions, using real-world data.
The flow-weighted young water fractions of the 22 Swiss catchments ranged from 0.07 ± 0.01 to 0.49 ± 0.03 (±SE), whereas the unweighted Fyw were slightly smaller, ranging from 0.06 ± 0.01 to 0.37 ± 0.03. The Fyw values from our study sites span roughly the 10th to 80th percentiles of the Fyw values estimated by Jasechko et al. (2016) for 254 rivers around the world. The median Fyw among the 22 Swiss catchments was 0.16 (95 % confidence interval 0.10–0.21), somewhat less than the global median of 0.21 (95 % confidence interval 0.19–0.24; Jasechko et al., 2016), consistent with Jasechko et al.'s (2016) observation that young water fractions tend to be smaller in steeper landscapes. Among the 22 Swiss catchments, Fyw and were positively correlated with catchment characteristics that control wetness conditions (e.g. mean monthly precipitation and mean precipitation intensity) and near-surface flow routing (e.g. drainage density and areal fractions of saturated soils; Sect. 5).
By calculating young water fractions for individual ranges of streamflow, we demonstrated that young water fractions generally increase with discharge (Q), and that this sensitivity of Fyw to Q varies from site to site (Sect. 6.1, Fig. 8). We developed a method to quantify the discharge sensitivity of Fyw through calculating the linear slope of the Q–Fyw relationship (Eqs. 6 to 9). The discharge sensitivity expresses how Fyw responds to changes in river discharge, which is used here as a proxy for catchment wetness and hydro-climatic forcing. Across our study catchments, the young water fraction and its discharge sensitivity were not correlated with each other, suggesting that these metrics represent different diagnostic indicators of catchment hydrologic behaviour (Sect. 6.2, Fig. 8). We hypothesize that low discharge sensitivities imply greater persistence in the relative contributions of fast and slow flow paths to streamflow during both high and low flows. High discharge sensitivities, however, imply shifts in flow path dominance during higher flows, such as when subsurface water tables rise into more permeable layers or the river network expands further into the landscape.
Based on our analysis, we developed a generalized conceptual description that relates Fyw and its discharge sensitivity to dominant streamflow generation mechanisms (Sect. 6.3, Fig. 10), which could be useful for analysing the effects of future climate change on catchment hydrological behaviour. It remains to be tested whether this conceptual description is transferable to other sites with landscape features and hydro-climatic forcing that are substantially different from our 22 Swiss study catchments.
The isotope data are available from Markus Weiler upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-3841-2018-supplement.
MW provided stream water isotope measurements. SS and SA modeled precipitation isotopes. JF and JK analyzed the data set. JF prepared the paper with contributions from JK, MW, SS and SA.
The authors declare that they have no conflict of interest.
The collection and analysis of the streamwater isotope data were mainly
funded as part of the National Research Programme NRP 61 by the Swiss
National Science Foundation within the project Drought-CH. We thank
Massimiliano Zappa from the Swiss Federal Research Institute WSL for
providing interpolated meteorological data for the 22 study catchments, and
Wouter Berghuijs for helpful discussions. Comments by Markus Hrachowitz and
Stefanie Lutz helped to improve the paper.
Edited by: Ralf Merz
Reviewed by: Markus Hrachowitz and Stefanie Lutz
Allen, S. T., Kirchner, J. W., and Goldsmith, G. R.: Predicting Spatial Patterns in Precipitation Isotope (δ2H and δ18O) Seasonality Using Sinusoidal Isoscapes, Geophys. Res. Lett., 45, 4859–4868, https://doi.org/10.1029/2018GL077458, 2018.
Benettin, P., Kirchner, J. W., Rinaldo, A., and Botter, G.: Modeling chloride transport using travel time distributions at Plynlimon, Wales, Water Resour. Res., 51, 3259–3276, https://doi.org/10.1002/2014WR016600, 2015.
Berghuijs, W. R., Sivapalan, M., Woods, R. A., and Savenije, H. H. G.: Patterns of similarity of seasonal water balances: A window into streamflow variability over a range of time scales, Water Resour. Res., 50, 5638–5661, https://doi.org/10.1002/2014WR015692, 2014.
BFS – Bundesamt für Statistik: GEOSTAT: Waldmischungsgrad der Schweiz, Neuchâtel, 1–12, 2004.
Birkel, C., Soulsby, C., and Tetzlaff, D.: Modelling catchment-scale water storage dynamics: reconciling dynamic storage with tracer-inferred passive storage, Hydrol. Process., 25, 3924–3936, https://doi.org/10.1002/Hyp.8201, 2011.
BLW – Bundesamt für: Minimales Geodatenmodell, 77.2 Digitale Bodeneignungskarte der Schweiz, Berne, 1–23, 2012.
Brantley, S. L., Eissenstat, D. M., Marshall, J. A., Godsey, S. E., Balogh-Brunstad, Z., Karwan, D. L., Papuga, S. A., Roering, J., Dawson, T. E., Evaristo, J., Chadwick, O., McDonnell, J. J., and Weathers, K. C.: Reviews and syntheses: on the roles trees play in building and plumbing the critical zone, Biogeosciences, 14, 5115–5142, https://doi.org/10.5194/bg-14-5115-2017, 2017.
Buttle, J. M.: Isotope hydrograph separations and rapid delivery of pre-event water from drainage basins, Prog. Phys. Geogr., 18, 16–41, https://doi.org/10.1177/030913339401800102, 1994.
Detty, J. M. and McGuire, K. J.: Topographic controls on shallow groundwater dynamics: implications of hydrologic connectivity between hillslopes and riparian zones in a till mantled catchment, Hydrol. Process., 24, 2222–2236, https://doi.org/10.1002/hyp.7656, 2010.
DeWalle, D. R., Edwards, P. J., Swistock, B. R., Aravena, R., and Drimmie, R. J.: Seasonal isotope hydrology of three Appalachian forest catchments, Hydrol. Process., 11, 1895–1906, https://doi.org/10.1002/(SICI)1099-1085(199712)11:15<1895::AID-HYP538>3.0.CO;2-#, 1997.
Dunne, T.,and Black, R. D.: Partial Area Contributions to Storm Runoff in a Small New-England Watershed, Water Resour. Res., 6, 1296–1311, https://doi.org/10.1029/Wr006i005p01296, 1970.
Feng, X. H., Faiia, A. M., and Posmentier, E. S.: Seasonality of isotopes in precipitation: A global perspective, J. Geophys. Res.-Atmos., 114, D08116, https://doi.org/10.1029/2008jd011279, 2009.
Feyen, H., Leuenberger, J., Papritz, A., Gysi, M., Fluehler, H., and Schleppi, P.: Runoff processes in catchments with a small scale topography, Phys. Chem. Earth, 21, 177–181, https://doi.org/10.1016/S0079-1946(97)85581-4, 1996.
Fischer, B. M. C., Rinderer, M., Schneider, P., Ewen, T., and Seibert, J.: Contributing sources to baseflow in pre-alpine headwaters using spatial snapshot sampling, Hydrol. Process., 29, 5321–5336, https://doi.org/10.1002/hyp.10529, 2015.
Godsey, S. E. and Kirchner, J. W.: Dynamic, discontinuous stream networks: Hydrologically driven variations in active drainage density, flowing channels and stream order, Hydrol. Process., 28, 5791–5803, https://doi.org/10.1002/hyp.10310, 2014.
Hale, V. C. and McDonnell, J. J.: Effect of bedrock permeability on stream base flow mean transit time scaling relations: 1. A multiscale catchment intercomparison, Water Resour. Res., 52, 1358–1374, https://doi.org/10.1002/2014WR016124, 2016.
Holko, L., Holzmann, H., de Lima, M. I. P., and de Lima, J. L. M. P.: Hydrological research in small catchments – an approach to improve knowledge on hydrological processes and global change impacts, J. Hydrol. Hydromech., 63, 181–182, 2015.
Horton, R. E.: The role of infiltration in the hydrologic cycle, Eos T. Am. Geophys. Un., 14, 446–460, 1933.
Hrachowitz, M., Soulsby, C., Tetzlaff, D., Dawson, J. J. C., and Malcolm, I. A.: Regionalization of transit time estimates in montane catchments by integrating landscape controls, Water Resour. Res., 45, W05421, https://doi.org/10.1029/2008WR007496, 2009.
Jasechko, S., Kirchner, J. W., Welker, J. M., and McDonnell, J. J.: Substantial proportion of global streamflow less than three months old, Nat. Geosci., 9, 126–129, https://doi.org/10.1038/Ngeo2636, 2016.
Jensen, C. K., McGuire, K. J., and Prince, P. S.: Headwater stream length dynamics across four physiographic provinces of the Appalachian Highlands, Hydrol. Process., 31, 3350–3363, 2017.
Kendall, C. and McDonnell, J. J.: Isotope tracers in catchment hydrology, Elsevier, Amsterdam, New York, 1–839, 1998.
Kirchner, J. W.: Aggregation in environmental systems – Part 1: Seasonal tracer cycles quantify young water fractions, but not mean transit times, in spatially heterogeneous catchments, Hydrol. Earth Syst. Sci., 20, 279–297, https://doi.org/10.5194/hess-20-279-2016, 2016a.
Kirchner, J. W.: Aggregation in environmental systems – Part 2: Catchment mean transit times and young water fractions under hydrologic nonstationarity, Hydrol. Earth Syst. Sci., 20, 299–328, https://doi.org/10.5194/hess-20-299-2016, 2016b.
Klaus, J. and McDonnell, J. J.: Hydrograph separation using stable isotopes: Review and evaluation, J. Hydrol., 505, 47–64, https://doi.org/10.1016/j.jhydrol.2013.09.006, 2013.
McGuire, K. J. and McDonnell, J. J.: A review and evaluation of catchment transit time modeling, J. Hydrol., 330, 543–563, https://doi.org/10.1016/j.jhydrol.2006.04.020, 2006.
McGuire, K. J., McDonnell, J. J., Weiler, M., Kendall, C., McGlynn, B. L., Welker, J. M., and Seibert, J.: The role of topography on catchment-scale water residence time, Water Resour. Res., 41, W05002, https://doi.org/10.1029/2004WR003657, 2005.
Nathan, R. J. and McMahon, T. A.: Evaluation of Automated Techniques for Base-Flow and Recession Analyses, Water Resour. Res., 26, 1465–1473, https://doi.org/10.1029/Wr026i007p01465, 1990.
Phillips, R. W., Spence, C., and Pomeroy, J. W.: Connectivity and runoff dynamics in heterogeneous basins, Hydrol. Process., 25, 3061–3075, https://doi.org/10.1002/hyp.8123, 2011.
Seeger, S. and Weiler, M.: Reevaluation of transit time distributions, mean transit times and their relation to catchment topography, Hydrol. Earth Syst. Sci., 18, 4751–4771, https://doi.org/10.5194/hess-18-4751-2014, 2014.
Song, C., Wang, G., Liu, G., Mao, T., Sun, X., and Chen, X.: Stable isotope variations of precipitation and streamflow reveal the young water fraction of a permafrost watershed, Hydrol. Process., 31, 935–947, https://doi.org/10.1002/hyp.11077, 2017.
Soulsby, C., Malcolm, R., Helliwell, R., Ferrier, R. C., and Jenkins, A.: Isotope hydrology of the Allt a' Mharcaidh catchment, Cairngorms, Scotland: implications for hydrological pathways and residence times, Hydrol. Process., 14, 747–762, 2000.
Soulsby, C., Tetzlaff, D., Rodgers, P., Dunn, S., and Waldron, S.: Runoff processes, stream water residence times and controlling landscape characteristics in a mesoscale catchment: An initial evaluation, J. Hydrol., 325, 197–221, https://doi.org/10.1016/j.jhydrol.2005.10.024, 2006
Soulsby, C., Tetzlaff, D., and Hrachowitz, M.: Are transit times useful process-based tools for flow prediction and classification in ungauged basins in montane regions?, Hydrol. Process., 24, 1685–1696, https://doi.org/10.1002/hyp.7578, 2010.
Spearman, C.: The proof and measurement of association between two things. By C. Spearman, 1904, Am. J. Psychol., 100, 441–471, 1987.
Staudinger, M., Stoelzle, M., Seeger, S., Seibert, J., Weiler, M., and Stahl, K.: Catchment water storage variation with elevation, Hydrol. Process., 31, 2000–2015, https://doi.org/10.1002/hyp.11158, 2017.
Stockinger, M. P., Bogena, H. R., Lücke, A., Diekkrüger, B., Cornelissen, T., and Vereecken, H.: Tracer sampling frequency influences estimates of young water fraction and streamwater transit time distribution, J. Hydrol., 541, 952–964, https://doi.org/10.1016/j.jhydrol.2016.08.007, 2016.
Tetzlaff, D., Seibert, J., and Soulsby, C.: Inter-catchment comparison to assess the influence of topography and soils on catchment transit times in a geomorphic province; the Cairngorm mountains, Scotland, Hydrol. Process., 23, 1874–1886, 2009.
Viviroli, D., Zappa, M., Gurtz, J., and Weingartner, R.: An introduction to the hydrological modelling system PREVAH and its pre- and post-processing-tools, Einviron. Model. Softw., 24, 1209–1222, https://doi.org/10.1016/j.envsoft.2009.04.001, 2009.
von Freyberg, J., Rao, P. S. C., Radny, D., and Schirmer, M.: The impact of hillslope groundwater dynamics and landscape functioning in event-flow generation: a field study in the Rietholzbach catchment, Switzerland, Hydrogeol. J., 23, 935–948, https://doi.org/10.1007/s10040-015-1238-1, 2015.
von Freyberg, J., Studer, B., and Kirchner, J. W.: A lab in the field: high-frequency analysis of water quality and stable isotopes in stream water and precipitation, Hydrol. Earth Syst. Sci., 21, 1721–1739, https://doi.org/10.5194/hess-21-1721-2017, 2017.
Whipkey, R. Z.: Subsurface stormflow from forested slopes, Int. Assoc. Scient. Hydrol., 10, 74–85, 1965.
Wilusz, D. C., Harman, C. J., and Ball, W. P.: Sensitivity of Catchment Transit Times to Rainfall Variability Under Present and Future Climates, Water Resour. Res., 53, 10231–10256, https://doi.org/10.1002/2017WR020894, 2017.
- Abstract
- Introduction
- Theoretical background: young water fractions from seasonal cycles of stable water isotopes in precipitation and streamwater
- Data set
- Methodological evaluation of the young water fraction framework
- Relationships between young water fractions, hydro-climatic conditions, and landscape characteristics
- Summary and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement
discharge sensitivityof Fyw and relate it to the dominant streamflow-generating mechanisms.
- Abstract
- Introduction
- Theoretical background: young water fractions from seasonal cycles of stable water isotopes in precipitation and streamwater
- Data set
- Methodological evaluation of the young water fraction framework
- Relationships between young water fractions, hydro-climatic conditions, and landscape characteristics
- Summary and conclusions
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement





