the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the dynamic nature of hydrological similarity
Hoshin Gupta
Conrad Jackisch
Martijn Westhoff
Axel Kleidon
Uwe Ehret
Erwin Zehe
The increasing diversity and resolution of spatially distributed data on terrestrial systems greatly enhance the potential of hydrological modeling. Optimal and parsimonious use of these data sources requires, however, that we better understand (a) which system characteristics exert primary controls on hydrological dynamics and (b) to what level of detail do those characteristics need to be represented in a model.
In this study we develop and test an approach to explore these questions that draws upon information theoretic and thermodynamic reasoning, using spatially distributed topographic information as a straightforward example. Specifically, we subdivide a mesoscale catchment into 105 hillslopes and represent each by a two-dimensional numerical hillslope model. These hillslope models differ exclusively with respect to topography-related parameters derived from a digital elevation model (DEM); the remaining setup and meteorological forcing for each are identical. We analyze the degree of similarity of simulated discharge and storage among the hillslopes as a function of time by examining the Shannon information entropy. We furthermore derive a “compressed” catchment model by clustering the hillslope models into functional groups of similar runoff generation using normalized mutual information (NMI) as a distance measure.
Our results reveal that, within our given model environment, only a portion of the entire amount of topographic information stored within a digital elevation model is relevant for the simulation of distributed runoff and storage dynamics. This manifests through a possible compression of the model ensemble from the entire set of 105 hillslopes to only 6 hillslopes, each representing a different functional group, which leads to no substantial loss in model performance. Importantly, we find that the concept of hydrological similarity is not necessarily time invariant. On the contrary, the Shannon entropy as measure for diversity in the simulation ensemble shows a distinct annual pattern, with periods of highly redundant simulations, reflecting coherent and organized dynamics, and periods where hillslopes operate in distinctly different ways.
We conclude that the proposed approach provides a powerful framework for understanding and diagnosing how and when process organization and functional similarity of hydrological systems emerge in time. Our approach is neither restricted to the model nor to model targets or the data source we selected in this study. Overall, we propose that the concepts of hydrological systems acting similarly (and thus giving rise to redundancy) or displaying unique functionality (and thus being irreplaceable) are not mutually exclusive. They are in fact of complementary nature, and systems operate by gradually changing to different levels of organization in time.
- Article
(5044 KB) - Full-text XML
- BibTeX
- EndNote
1.1 Motivation
This paper addresses the following question. “How important is spatial variability of terrestrial system characteristics and meteorological forcing when viewed from the perspective of streamflow generation and distributed water storage?” While this question has motivated hydrologists since the early days of our science, it gained substantial attention with the development of distributed hydrological models, and it seems fair to say that attempts to address the question still lie at the heart of every distributed model application (Beven, 1989; Freeze and Harlan, 1969; Refsgaard, 1997; Hrachowitz and Clark, 2017a).
Needless to say, this question has not found easy answers. In addition to the lack of sufficient process understanding (in part due to the difficulty of gathering relevant data about hydrologic systems), there is also the uncertainty we unavoidably encounter when dealing with the steadily growing and changing pool of geoinformation (Musa et al., 2015). For instance land surface digital elevation information is now available at a resolution of 25 m globally (Farr et al., 2007). Similarly, weather radar coverage is available for large parts of Europe, providing accumulated 15 min precipitation estimates at 4 km resolution (Huuskonen et al., 2014). Despite the huge potential for model improvement provided by these new and diverse pools of information, a danger associated with their use is that we can “miss the forest for the trees” unless we are able to determine which information contained in the data is of relevance to the questions we seek to answer.
We therefore now face the problem of how to discriminate important details about the hydrological landscapes from idiosyncratic ones, and hence must deal with the challenge of how to identify which characteristics explain hydrological similarity (Blöschl and Sivapalan, 1995). This study is largely motivated by the power view introduced by Wagener and Gupta (2005) which advocates “a need to develop better methods for characterizing and extracting relevant information from data” (see also Gupta and Nearing, 2014). Our specific objective is to propose an approach addressing this issue, by drawing upon an information theoretic perspective to extract and quantify the relevant information for spatially distributed hydrological modeling, and by using thermodynamic reasoning to explain why only a portion of the full information content available in the data is relevant.
1.2 Background
From a thermodynamic perspective, streamflow generation is driven by differences in potential energy between the upslope catchment areas and the stream channel. The majority of this available energy is dissipated during runoff concentration and infiltration, while the remaining part is exported from the catchment as the kinetic energy of streamflow (Kleidon et al., 2013). These potential energy differences depend largely on catchment topography and on the space–time patterns of precipitation (Zehe et al., 2013). Accordingly, we might be naturally drawn to expect that large spatial variations in both characteristics will result in large spatial variations in runoff generation. However, when exactly should spatial variation be considered large enough that we need to explicitly account for it?
In the context of spatially distributed rainfall, this latter question has received considerable attention (e.g., Obled et al., 1994; Arnaud et al., 2002; Tetzlaff et al., 2005; Zehe et al., 2005; Das et al., 2008). In general, the predominant view that seems to emerge from these studies is that the impact (on runoff simulations) of spatial distribution in rainfall increases with size of the area considered. This is often traced back to the growing importance of flood routing, in combination with the average spatial extent of typical rain storms (e.g., Smith et al., 2004; Lobligeois et al., 2014). Nevertheless, no consensus has yet emerged as to whether this statement is generally valid, and no guidelines exist regarding under which conditions the use of information regarding the spatially distributed nature of rainfall becomes inevitable (Emmanuel et al., 2015).
Similarly, the question of how strongly the spatial resolution of a digital elevation model (DEM) affects the results of a distributed model application has been investigated in various studies (e.g., Schoorl et al., 2000; Thompson et al., 2001; Sørensen and Seibert, 2007). For instance Zhang and Montgomery (1994) varied the resolution of their DEM and reported that spatial resolutions finer than 10 m did not result in significant improvements to the simulation results of their hydrological model. Chaubey et al. (2005) tested the influence of DEM spatial resolution on simulation results of the Soil Water and Assessment Tool (SWAT) and reported that grid size has a significant influence on different watershed responses, as well as on the sub-basin classification implemented in SWAT. However, as with the case of distributed rainfall, the results of these studies do not point to a generic approach, nor to any general conclusions regarding the importance of DEM resolution for distributed hydrological modeling.
Overall, this lack of a coherent image certainly reflects the varying sensitivities of different model structures (Das et al., 2008), the dependence on scope and scale of the model exercise (Blöschl and Sivapalan, 1995), and the dependence on differences among hydrological landscapes (Beven, 2000). It seems, therefore, that an investigation of the role of distributed information in hydrological modeling may benefit from a more generic and systematic approach, one that may be generalized to different spatially distributed data sources and models and that is able to cope with interactions among them in a straightforward manner. In contrast to much of the aforementioned work, which has relied primarily on statistical methods, the purpose of the work reported here is to investigate the extent to which information theory (Cover and Thomas, 2005) is able to provide instructive measures that are suitable for this purpose.
More specifically the main objective of this study is to present and test an approach to quantify the relevance of spatially distributed data sources for hydrological simulations drawing from information theory. We exemplify this approach using catchment topography as distributed information source as well as streamflow and soil water storage as modeling targets; however, the general mindset of the approach is applicable to any distributed information source such as spatially distributed rainfall or geology as well as to a wide range of arbitrary model target and different distributed models.
1.3 The role of surface topography in hydrological modeling
Despite the fact that DEMs provide the basis for identifying watershed boundaries, river networks and potential energy differences in the landscape, several studies have concluded that topography alone is a weak descriptor for inferring similarity in hydrological behavior. For instance, Zehe et al. (2005) showed that the topographic wetness index (Beven and Kirkby, 1979), a popular topographic similarity measure, failed to explain soil moisture variability and similarity in runoff generation in a lower mesoscale catchment. Fenicia et al. (2016) and Jackisch (2015) showed that topography alone might be a poor guide for subdividing a 256 km2 catchment into different functional units and questioned the explanatory power of the topography in this respect. Our own work, Loritz et al. (2017), has shown that an effective representation of two different catchments by a single representative hillslope was able to provide successful simulations of their inter-annual runoff responses and annual storage dynamics. Together, these findings suggest that an informationally “compressed” representation of the topographic map may be able to preserve the relevant information regarding geopotential differences that drive runoff generation.
In line with these findings, we therefore pose the hypothesis that “although a highly resolved DEM contains a large amount of information about topography, not all of this spatially distributed information is relevant for the generation of hydrological predictions”. Following Weijs et al. (2013b), it seems reasonable that information theory may provide a natural framework for dealing with such compression of information in hydrologic science. The term “compression” was originally coined by Claude Shannon to refer to the quantification, storage and communication of information (Shannon, 1948). In environmental science, information theoretic concepts such as the Shannon entropy have found widespread use in various applications (e.g., Brunsell, 2010; Weijs et al., 2013a; Yakirevich et al., 2013), ranging from uncertainty assessment in 3-D geological models (Schweizer et al., 2017) to the delineation of water resource zones in Japan (Kawachi et al., 2001). For an introduction to, and detailed review of, information theoretic concepts we refer the reader to Cover and Thomas (2005), Singh (2013), and Weijs and van de Giesen (2013).
With respect to the above finding it is important to note that compressibility relates to order or organization (Davies, 1990). The identification of relevant information within distributed system characteristics is therefore closely linked to the identification of spatial organization and thus with the identification of hydrological similar functioning areas (Sivapalan, 2005). As pointed out by Zehe et al. (2014), these functional units may be straightforwardly defined in thermodynamic terms as any flux that is driven by a specific gradient while it performs work against a specific flow resistance. Similarity of both the relevant drivers and the resistance terms is a sufficient criterion to expect that two systems behave similarly with respect to the generation of a flow and with regard to the associated entropy production.
If we transfer this concept to runoff generation, differences in the geopotential (topography) act as a driver since runoff is driven by gravity. The resistance term, on the other hand, depends either on surface roughness (and thus for instance on the vegetation in case of overland flow), on the pattern of subsurface conductance, on apparent preferential pathways and in case of matrix flow on the capacity of the system to store water. Yet, the gradient flux-resistance relation is non-unique, because a twice as large driver in combination with a twice as large resistance results in exactly the same flux. It is this non-uniqueness that explains why two hillslopes with distinctly different topographies may still produce the same runoff when these differences are compensated by their associate resistances.
However, while a physical explanation of the landscape organization phenomenon is crucial to our understanding, for practical modeling applications we need to step beyond that and actually identify these functional units in the landscape. One avenue is surely to detect these gradients and resistance terms directly based on the available landscape characteristics (Seibert et al., 2017). However, it is often difficult to know a priori which characteristics dominate the function of a landscape element (Oudin et al., 2010). Another approach is, hence, to identify functional units a posteriori directly based on their function and to subsequently identify which characteristics dominate the hydrological processes, and at which scale (Sivapalan et al., 2003). It is exactly here that an information theoretic perspective might be particularly valuable as, despite the more qualitative and descriptive nature of the concept of landscape organization, compressibility is actually quantifiable. For instance two hillslopes showing a similar function with respect to a given process can be compressed and hence combined into a larger landscape element without losing information about the spatial distribution of processes in a catchment. The identification of functional similar areas is hence directly connected to both statistical physics (organization) and information theory (compressibility). For this reason we believe that concepts such as maximum (Shannon) entropy (Jaynes, 1957) and information theoretic variables like the mutual information and Kullback–Leibler divergence (Cover and Thomas, 2005; Weijs et al., 2013b; Weijs and van de Giesen, 2013) provide an excellent framework for connecting the generic informational concepts of statistical inference and compression of data with the specific domain concepts of landscape organization and hydrological similarity.
1.4 Objectives and scope
The main objective of this study is to propose and test a generic approach, based on information theory, and to quantifying the relevance and value of spatially distributed data sources for hydrological simulations. Our approach is developed and tested using catchment topography as the source of spatially distributed information and using streamflow and soil water storage as the modeling targets. Specifically, we subdivide a 19.4 km2 catchment into 105 hillslopes and represent each of these contributing spatial units with a hydrological hillslope model. Following Loritz et al. (2017), the hillslope models are identically parametrized with respect to soils, bedrock topography and vegetation, and they differ only with respect to the values of their topography-dependent parameters such as aspect, slope and elevation above, and distance to the river. Each of these hillslope models is driven by the same meteorological forcing for 1 hydrological year yielding 105 independent runoff and storage time series. In the first part of this paper we analyze the distributions of runoff and storage simulations at each time step by means of the Shannon information entropy. With this approach we are able to reveal different levels of redundancy in our simulated output in time and try to answer the question of whether we can identify the necessary spatial complexity of our chosen model structure. In the second part of this paper we evaluate the similarities of the runoff time series simulated by the hillslope models in terms of their mutual information. We use this as a basis for compressing them into a smaller set of functional groups, such that in each group the members are to a certain extent predictable from each other in terms of runoff generation. Here we choose the average Shannon entropy of the simulation period to determine the number of different functional groups. Based on this we construct different time-invariant realizations of a compressed catchment model and test those against observations and the simulation with the uncompressed model. Finally, we reiterate that the overall approach presented here is applicable to a variety of different spatially distributed information such as spatially distributed rainfall or land use, as well as to most modeling targets and to a wide range of spatially distributed hydrological models available. This paper is, however, restricted to development and testing of the approach using only catchment topography and one numerical hillslope model.
In this section we introduce the study area, the database used and the general model setup of the different hillslopes.
2.1 The Colpach catchment
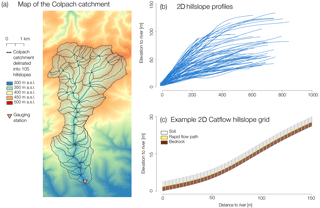
The 19.4 km2 Colpach catchment is situated in the northern part of the Attert basin in the Devonian schists of the Ardennes massif and has an elevation ranging from 265 to 512 m a.s.l. (Fig. 1a). Approximately 65 % of the catchment is forested, mainly on the steep hillslopes. In contrast, the plateaus at the hilltops are predominantly used for agriculture and pasture. The dominant runoff process is rapid flow in a highly permeable saprolite layer above the bedrock, and the catchment is characterized as a fill-and-spill system (Wrede et al., 2015). In addition to the importance of lateral flow along the bedrock, several irrigation and dye-staining experiments have highlighted the role of vertical structures for infiltration and subsequently for subsurface runoff formation (Jackisch et al., 2017). For a more detailed description please see Loritz et al. (2017), Wrede et al. (2015) and Jackisch (2015).
2.2 The CATFLOW model
The spatially distributed hillslope-scale model CATFLOW (Maurer, 1997; Zehe et al., 2001) is based on the subdivision of a catchment into several hillslopes connected by a drainage network. Each hillslope is discretized along a two-dimensional cross section using curvilinear orthogonal coordinates. Each surface model element extends over the width of the hillslope, and these widths may vary along the hillslope. Evapotranspiration is represented using an advanced SVAT (soil–vegetation–atmosphere transfer) approach based on the Penman–Monteith equation, which accounts for tabulated vegetation dynamics, albedo as a function of soil moisture, and the impact of local topography on wind speed and radiation. Soil water dynamics and solute transport are simulated based on the mixed form of the Darcy–Richards equation, solved using the mass conservative Picard iteration and adaptive time stepping (Celia et al., 1990). The hillslope module is designed to simulate infiltration excess runoff, saturation excess runoff, re-infiltration of surface runoff, lateral water flow in the subsurface, return flow and solute transport.
2.3 Hillslope setup, forcing and model evaluation
The topographic analysis was based on a 5 m lidar digital elevation model, aggregated and smoothed to 10 m resolution. GRASS GIS (Neteler et al., 2012) was used to subdivide the catchment into 105 hillslopes (Fig. 1a) using a classical hydrological terrain analysis algorithm r.watershed. This approach generates a stream network after the user sets a threshold for the minimum size of an exterior watershed basin. We identified this value by varying this threshold across a range of values trying to reproduce the official stream network which was available from the Luxembourg Institute of Science and Technology (LIST) by visual inspection. Following the standard procedure of r.watershed each stream segment has two corresponding hillslopes (left and right side of the stream). We use the landscape units mapping program (LUMP; Francke et al., 2008) and again GRASS GIS to derive the hillslope profiles, including properties such as the elevation and distance to the river, and the mean aspect and width function of each hillslope (Fig. 1b). On average the hillslopes lie 67 m above the river, are 446 m wide and cover an area of 0.16 km2. The maximum area of a hillslope is 0.86 km2 while the smallest hillslope covers an area of 0.12 km2.
With respect to soils, bedrock topography and vegetation, the 105 hillslope models were identically parameterized using a parameter set, macropore distribution and subsurface stratification tested and derived by Loritz et al. (2017) when representing the entire Colpach catchment by a single effective hillslope model. Accordingly the hillslopes differ only in the values of parameters that are extracted from the digital elevation model (hillslope profile and length, width and aspect). All hillslope models are 2 m deep, where the upper 1 m is classified as soil followed by a 0.2 m lateral saprolite layer and an 0.8 m deep almost impermeable bedrock (see soil parameter and structure in Table 1 in Loritz et al., 2017). The porosity of the upper 1 m of soil is assumed to reduce linearly with depth, with the lowest value being 0.3 at a depth of 1 m from the surface. In order to account for reported preferential flow in this area (Jackisch et al., 2017) we added additionally, every 4 m, a 0.1 m wide rapid flow path (vertical flow structure) with a depth of 1 m. The entire soil setup follows the findings of Loritz et al. (2017) in which it was shown that a representative hillslope was able to provide successful simulations of various hydrological fluxes. The discretization of the hillslope in the downslope direction varies between a maximum of 1 m and minimum of 0.1 m, where the latter occurs close to rapid flow paths. The vertical grid size was set to 0.1 m, with a reduced vertical grid size of the top node of 0.05 m (Fig. 1c).
Boundary conditions were set to an atmospheric boundary at the top, no-flow boundary conditions at the upslope and a gravitational flow boundary condition at the lower boundary. At the hill foot of the hillslope we selected a seepage interface for the upper 0.4 m, where outflow only occurs under saturated and no flow under unsaturated conditions. For the lower 1.6 m of the downslope boundary we selected a no-flow boundary to mimic a saturated zone close to the river. All of the hillslopes are covered entirely by forest and the evapotranspiration routine is parameterized similarly to the one described in detail in Loritz et al. (2017). Figure 1c shows an example of a typical CATFLOW hillslope grid and soil setup divided into soil, rapid flow paths and bedrock.
2.3.1 Model forcing and application
Meteorological input data are recorded at an official meteorological station (Roodt) and were provided by the “Administration des Services Techniques de l'Agriculture Luxembourg”. All hillslope models were forced with identical meteorological inputs. This implies, for instance, that we neglect observed variations of rainfall and wind speed within the catchment. We compared simulated and observed specific runoff by dividing the respective values by the relevant contributing areas, i.e., either by the area of the hillslope or of the Colpach catchment. Similarly, we calculated the area specific water storage (average water content per m2) for each hillslope. The simulation period is the hydrological year 2014 from October 2013 to October 2014. This is preceded by a model spin-up of 1 year with initial states of 70 % saturation.
2.3.2 Model evaluation
The intention of the model evaluation performed here was not to infer whether we have identified the best-performing model structure, but to evaluate and quantify differences in modeled runoff and storage arising from underlying differences in hillslope topography. Therefore, while this exercise does not require a comparison to observations, we nevertheless do so to demonstrate that the different models (and in particular the entire ensemble) produce meaningful simulations that are consistent with observed hydrological storage and streamflow dynamics. We inspected the runoff simulations both visually and by comparison to the observed specific discharge using the normalized mutual information (NMI, specified below; see also Michaels et al., 1998). In addition, we use the Kling–Gupta efficiency (KGE, Gupta et al., 2009) to highlight that the NMI provides a consistent picture and is able to identify differences between hydrographs. Furthermore, we use the NMI in our functional classification because it is symmetric and satisfies the mathematical requirements of a distance metric (see Sect. 2.6; for a further comparison of the NMI as well as the Appendix C). Additionally, we calculated the KGE and NMI between the area-weighted median of the runoff simulations and the observed specific discharge of the catchment. By simply using the area-weighted median instead of a river network routing scheme, we assume, in line with Robinson et al. (1995) and our own findings (Loritz et al., 2017), that the Colpach catchment is hillslope dominated and that the timing of the routing is small enough to be neglected.
With respect to the storage dynamics, we estimated the average amount of water within the hillslope (in mm for each hillslope) and compared these values against the median of storage estimates calculated from available soil moisture measurements in 10, 30 and 50 cm, which have been collected at different locations throughout the catchment (for detailed information of the soil moisture sensors and observations please see Loritz et al. (2017). As the model and the observations estimates are based at largely different scales, we believe that any comparison more detailed than the comparison of their temporal dynamics is inappropriate.
In the following section we provide a detailed review of the important concepts from information theory and discuss how we used these concepts to address the study objectives.
3.1 Information theory and Shannon information entropy
The field of information theory originally developed within the context of communication engineering deals with the quantification of information with respect to a concept called surprise (Applebaum, 1996). For a discrete random variable X that can take on several values X ∈ {x1; x2; x3 … xi} with associated prior probabilities p(x1) p(x2); p(x3) … p(xi), the surprise or information content of receiving/observing a specific value X = xi is defined as
where I is the information content, k is the base of the logarithm and p(xi) the prior probability that X can exist in the state x. The logarithm in this definition assures that information is an additive quantity. When the base k of the logarithm is chosen to be 2, information is measured in “bits” (abbreviated from binary digit). While different k values can be used to calculate the information content of a random discrete variable, here we stick with the logarithm to the base 2.
To calculate the average information content associated with the random variable X we can estimate the Shannon entropy H(X) defined (by taking its expectation) as
where p(xi) is again the probability that X can be in the state x. In this study we computed the Shannon entropy of the probability distribution of the 105 runoff and storage simulations for each hourly time step. In addition to computing the Shannon entropy for a single random variable (also called self-information), we compute the joint entropy H(X, Y) of a set of variables X and Y as follows:
where p(xi, yi) is the joint probability. The joint entropy is used to estimate the mutual information (described below) between two random variables. For more detailed discussion of information theoretic concepts and variables please see Applebaum (1996) and Cover and Thomas (2005).
3.1.1 The appropriate binning for estimating discrete probability density functions
A crucial step in the computation of Shannon entropy and/or mutual information of discrete distribution (see Sect. 3.1 and 3.2) is a careful choice of the bin widths used to construct the probability density functions (pdf; Gong et al., 2014; Pechlivanidis et al., 2016). Various guidelines are available regarding how to properly estimate the bin width from the viewpoint of statistical rigor (e.g., Scott, 1979). However, Weijs and van de Giesen (2013) also point out that the bin width for a pdf should always be chosen based on considerations related to the question one wishes to answer. For instance, hydrologists often evaluate their models against measured soil moisture or discharge data. As such observations always imply the existence of measurement errors, observational differences smaller than the typical size of such errors should not be afforded physically meaningful importance. (To infer on the sensitivity of the Shannon entropy to different bin width please see the Appendix B.)
Accordingly, for calculation of the entropy of the runoff and the storage simulations we propose that the smallest meaningful bin width should be greater than or equal to the measurement error. Consequently, we choose the mean relative error of the rating curve (8.5 %, see Appendix A) to estimate the Shannon entropy of the runoff simulations and the measurement error of the installed capacitive soil moisture probes of 1 vol % for the storage simulations (Decagon 5TE; ±1–2 % volumetric water content for calibrated soils; manufacturing information). For the runoff simulations, we started with a bin width of 0.01 mm and then progressively increased the bin width by a factor of 8.5 %. This results in a non-uniform bin width distribution with constantly increasing bin sizes for larger discharge values as the uncertainty in the measurements increases with higher flows. In contrast, for the storage simulations, we used a constant bin width of 10 mm because the measurement errors of our soil moisture probes do not depend on the magnitude of the measured value. We transferred the error of the soil moisture probes to our storage simulations as follows. The 1 m thick soil domain has a porosity of 0.57 (m3 m−3), having a total storage volume of 570 mm. We hence use a constant bin width of 10 mm, corresponding to 1 % vol, with bins ranging from 10 mm (1 % vol) to 570 mm (57 % vol).
3.1.2 Upper and lower boundary of the Shannon entropy – perfect versus no organization
Isolated systems evolve, according to the second law of thermodynamics, to a state of maximum entropy in which all gradients are depleted and each microstate of the system is equally likely (Kondepudi and Prigogine, 1998). This implies maximum uncertainty about the microstate and the absence of any organization/order in the system. Jaynes (1957) transferred this fundamental insight into a method of statistical inference, stating “when making inferences based on incomplete information, the best estimate for the probabilities is the distribution that is consistent with all information, but maximizes uncertainty”. This condition is reflected by a uniform distribution where all outcomes are equally likely (Weijs et al., 2010). With respect to our model ensemble, a state of maximum entropy implies that each of the 105 hillslope models produces a unique output that cannot be guessed given knowledge regarding the output of any other hillslope. Accordingly, we can calculate the theoretic maximum entropy for our model as
where N = 105 is the number of hillslope models. This maximum reflects a theoretical state of zero spatial organization in the catchment, where each hillslope provides a unique contribution to streamflow and storage dynamics due to its specific topography. A further compression of the catchment subdivision, for instance by leaving out or merging certain hillslopes, is not possible without losing precision. At the other end of the spectrum, one may have a state of perfect spatial organization in which all 105 hillslope models are within the error margin of observations perfectly predictable from each other. This would correspond to zero entropy and implies that the compression of the spatially distributed model is trivial as any arbitrarily selected hillslope will represent it equally well.
It is important to note that Hmax is (in our virtual experiment) a theoretical upper limit as the hillslope models would, given our bin width, need to simulate discharge values as high as 48.3 mm h−1 to reach this theoretical limit. We thus distinguish between the maximum entropy of our model ensemble given the spatial discretization of the model and the maximum entropy of our experiment given the uncertainties and physical limits of our discharge and storage simulations and observations. The difference becomes clear if one imagines a simple thought experiment in which one would like to study a dice with six possible outcomes. The maximum entropy of this dice is linked to the number of possible states of the system and hence is log2(6) = 2.58. Now depending on our investigation, we might change our question and only ask for values larger or smaller than 3. In this case the maximum entropy of our experiment would, with two possible outcomes, be log2(2) = 1.
3.2 Mutual information as similarity measure
To compare simulated runoff time series generated by different hillslopes, we calculate the pairwise mutual information of each simulated runoff time series as a similarity measure. Mutual information I(X, Y) between two discrete random variables X and Y is a measure of the strength of their informational correspondence, defined by Cover and Thomas (2005) as
where p(x, y) is the joint probability of X and Y, and p(x) and p(y) are their marginal probabilities. Equivalently, mutual information can also be calculated directly as a difference between the sum of the entropies of X and Y minus the joint entropy of X and Y (Fig. 2).
While Shannon entropy is used to determine the information redundancy or compressibility between the 105 simulated discharge time series at certain time steps, we now show how mutual information can be used to see how similar or dissimilar two discharge simulations are.

Figure 2Sketch of the relation between information entropy, joint entropy and mutual information displayed as bar diagram.
Mutual information quantifies the amount of information that one variable reveals about another and thus the strength of their codependence. If the mutual information is zero, the two variables are independent while larger values correspond to stronger relationships. When using the binary logarithm mutual information, Shannon entropy and joint entropy share the same unit bits. Here, we seek to use the mutual information between different hillslope runoff simulations as a measure of similarity or distance between the hillslope models. However, since the value of mutual information depends on the absolute magnitude of joint entropy between the two chosen variables, it is not appropriate to use mutual information directly as a distance function for relative comparisons (if the joint entropy of two variables is low the value of mutual information will also be low even if the two variables are perfectly related). Hence, following Michaels et al. (1998), we normalize I(X, Y) using the larger of the entropies of the two random variables X and Y. It is important to note that this normalization can also be done using the smaller of the entropies of the two random variables X and Y or the joint entropy of X and Y. Depending on the objective this can be an important choice (see Appendix C). In this study we follow the avenue recommended by Michaels et al. (1998) and use the maximum.
Accordingly, the normalized mutual information ranges from 0 to 1, with higher values corresponding to stronger relationships (higher mutual information content). Further, to make the NMI easier to interpret we subtract the NMI from 1 as typical distance functions are normally closer to zero in case of a stronger similarity (see Appendix C for a comparison of the NMI with the Pearson correlation coefficient and the Euclidean distance).
3.3 Functional classification of hillslopes with similar runoff behavior
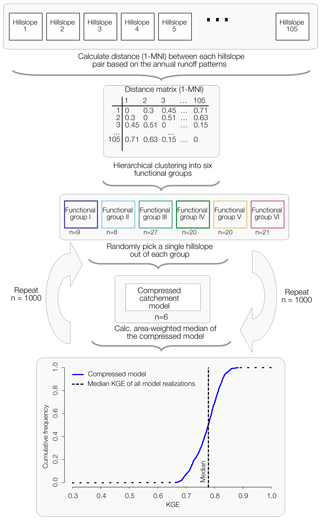
Using NMI as a distance metric, we classified the 105 hillslope models into functional groups of similar runoff behavior based on the 105 runoff time series, using a hierarchical cluster analysis based on Ward's minimum variance method (Hastie et al., 2009; Murtagh and Legendre, 2014). As a first guess of a physically meaningful number of functional groups we used the mean annual entropy of all 105 discharge simulations (further discussed in Sect. 4.2).
This choice is inspired by the fact that the Shannon entropy of a random variable X is closely related to the maximum compressibility of the information about this variable. This is because, when the Shannon entropy is calculated using the binary logarithm, it relates to the minimum number of binary yes or no questions necessary to determine the actual value of xi from X. In the special case where the distribution of the random variable is dyadic, the value of the Shannon entropy H(X) and the expected minimum number of questions are equivalent, while if this is not the case the expected number of questions lies between the computed value of the entropy H and its increment H + 1 (for further details see Cover and Thomas, 2005).
So, in general, if the entropy of a discrete random variable X is H(X) = 2, we know that the expected number of binary (yes or no) questions needed to quantify x lies between 2 and 3. This implies that the number of possible outcomes lies somewhere between 22 = 4 and 23 = 8, as every binary question can have two possible answers.
3.4 Compression of the catchment model based on functional groups
Having grouped the hillslope models into time-invariant functionally similar groups, we test whether this grouping provides a solid basis to compress the model structure of 105 hillslopes into a less redundant one that yet produces results of similar quality as the full set of hillslopes but at much smaller computational cost. There are at least three avenues to do so. The first one is to simply calculate the area-weighted median or average of all runoff simulations within a functional group. This, however, means that all 105 runoff simulations are necessary to build this compressed model and we cannot run the compressed model in a forward mode. The second avenue is to take functionally united hillslopes and derive for each functional unit an effective, spatially aggregated hillslope in a similar fashion as done in Loritz et al. (2017). Though this is most likely the most promising way to come up with a compressed catchment model, it is beyond the scope of this paper. Instead, to simplify this attempt in this study we use a third option and develop a compressed model structure using a bootstrap-like approach. For this we randomly select a single hillslope from each functional group and calculate the area-weighted median of the simulated discharge time series of the six randomly selected hillslope models (compressed catchment model; Fig. 3). The weight assigned to each of the selected discharge time series corresponds to the areal fraction of all hillslopes in the respective functional group. This assures mass conservation because runoff of each hillslope is equal to its area times the simulated specific discharge. We use random selection because each group member is regarded as equivalent to represent the runoff generation of the corresponding functional group. To account for sampling variability, as simulated runoff differs slightly among the hillslopes within a functional group, we repeat this random selection 1000 times. In a final step, we compare those values individually as well as the median of all realizations against the observed runoff of the Colpach catchment using the KGE. This reveals the performance spread of the randomly generated compressed models compared to the area-weighted median of the entire 105 hillslopes.

Figure 4(a) Observed and simulated runoff of the Colpach catchment. The red lines correspond to individual hillslope models and the yellow line to the area-weighted median of all hillslopes. (b) Simulated total area specific storage of each hillslope in red and the median of all models in yellow. The median of the 141 observed soil moisture time series is smoothed with a 12 h rolling mean (for more detail to the soil moisture observation we refer to Loritz et al., 2017). (c) Shannon entropy in turquoise for the runoff simulations as well as the corresponding mean and (d) a similar plot for the storage simulations (red).
4.1 Runoff and storage simulations
The overall model performance of the area-weighted median of all hillslopes is decent, with a KGE of 0.76. The ability of different hillslope models to reproduce the observed runoff dynamics of the Colpach catchment varies substantially (see Fig. 4a), with KGE values ranging between 0.44 and 0.92. This apparent spread in model performance among the hillslopes corroborates the sensitivity of simulated discharge to those parameters derived from the DEM. A similar pattern is revealed when model goodness is expressed by means of the normalized mutual information between each hillslope model and the observed runoff. NMI values range from 0.51 to 0.71 and show a strong linear correlation to the corresponding KGE values (with a Pearson correlation coefficient of 0.89). This good correspondence of NMI with the KGE performance measure reinforces the notion that NMI is a suitable measure of similarity, or difference, between time series of hydrological variables.
The temporal patterns of total area specific storage for each hillslope model are shown in Fig. 4b. The skill of different hillslopes to reproduce the temporal dynamics of observed median storage is rather stable, with a Spearman rank correlation coefficient ranging from 0.77 to 0.86, with the ensemble median having a value of 0.82. Visual comparison of the simulated storage time series reveals that differences in hillslope topography result mainly in a parallel shift of the respective time series. This parallel spreading is stronger during the wet season and less pronounced during dry conditions. The latter might be due to the identical vegetation parameterization of each hillslope and hence a result of highly similar root water uptake which dominates storage dynamics during dry conditions in summer.
4.2 Entropy of the discharge and storage simulations
If all 105 of the hillslope models were to produce unique simulations of equal importance, their entropy would be the theoretical maximum value of log2(105) = 6.7. However, in our study the maximum entropy of our discharge simulations given the chosen binning size and the maximum simulated discharge value of 0.75 mm h−1 is log2(54) = 5.7 and for the storage simulation given a minimum simulated soil moisture close to 200 mm and a maximum around 400 mm log2(21) = 4.4. On the other side of the spectrum the minimum of the Shannon entropy associated with a perfectly redundant set of hillslopes is 0.
Table 1Number of members as well as the mean and max values of the runoff simulation of each functional group.
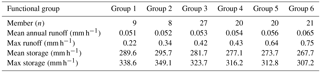
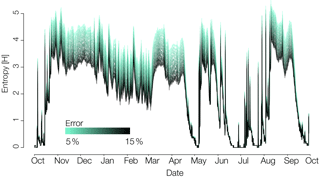
As seen in Fig. 4c and d, the entropy of the ensemble of runoff simulations starts at a rather low value at the beginning of our simulation period, increases with the first rainfall events in autumn, stays at a high level (ranging between 3 and 4) during the winter period and starts to decrease towards 0 in May. During the summer, the entropy reacts much more strongly to the different rainfall events than in winter and peaks at a value of 4.9 in August (35 from 54 bins allocated) when streamflow production grows again after a long dry period of low flow. It is interesting to note that the entropy in simulated streamflow is highly dynamic in time, implying that the required structural resolution of the model changes with time, with the 105 hillslope models' structure being less redundant during periods of high entropy and more strongly redundant when entropy approaches 0 (see also Appendix D).
For the ensemble of storage simulations, the entropy varies between 1.5 and 2.9, which indicates less temporal variability compared to runoff. This is consistent with the visual impression that differences in topography result mainly in a parallel shift of the time series to a different annual mean. Nonetheless, the entropy time series exhibits weak annual dynamics, with a peak in mid-November when the wet season starts. This peak coincides with the entropy peak of the runoff simulations. In spring and summer, the entropy decreases slowly until it reaches the overall minimum of 1.71 in October. Note that this could be very different in the case of (for instance) land-use differences or distributed rainfall among the hillslopes causing a likely increase in entropy during summer and autumn.
4.3 Functional group and their typical runoff and storage dynamics
The mean annual entropy of the runoff simulations is 2.5 (Fig. 4c), which implies that (on average) the number of functional groups or bins that can be distinguished lies between 22.5 ≈ 6 and 23.5 ≈ 10. In line with one of our goals to use information theoretic measures to define similar-acting landscape elements and to compress the full catchment model into functional groups without substantial loss of information we took the lower value and used a hierarchical cluster analysis to classify the hillslopes into six functional groups using normalized mutual information (1-NMI) as a distance metric. The median discharge for each functional group is shown in Fig. 5a, while the corresponding set of hillslope profiles is displayed in Fig. 5b. In general it seems that the functional groups 1, 2 and 6 exhibit the strongest differences with respect to their median runoff time series as well as with respect to the geopotential profiles, whereas the classes 3–5 appear much more similar in both aspects. The median of the storage simulation of each functional group is displayed in Fig. 5c. Consistently with simulated runoff, the storage time series of functional groups 1, 2 and 6 show the greatest differences. However, in contrast to the runoff simulations also the functional groups 3–5 are better separable at least during the wet period. Consistent with the decline of the Shannon entropy in Fig. 4d these differences diminish in summer. Especially in June, July and August all of the functional groups simulate essentially identical storages as their differences are getting closer to the error margins of the soil moisture measurements. Again, we stress that this convergence could be explained by the dominant role of evapotranspiration and the identical land-use parameterization of all hillslopes. Note that functional group 6 shows the strongest and fastest overall runoff reaction and has the lowest overall storage simulation. Consistent with that, functional group 1 and 2 show the slowest runoff reaction and are characterized by the highest overall storage.
4.4 Performance of the compressed catchment models
Figure 6 shows the cumulative frequency distribution of KGE values for the 1000 randomly selected model compressions using the aforementioned functional groups of similar runoff generation (Table 1). The median of all 1000 KGE values of all trials is 0.78 and corroborates that the compressed model structures perform on average slightly better than the area-weighted median of the 105 hillslope models, which has a KGE of 0.76. However, the range of 0.66 to 0.88 in the KGE values indicates that the performance of a particular single realization of the compression depends on the actual combination of hillslopes selected for each group. As each realization of the compressed catchment model would in principle only use six hillslope models and if we assume that all hillslopes have the same run time, this could, in theory, reduce the computational costs of our model application by a factor of 17.5.

Figure 5(a) Median runoff of the six functional groups; (b) corresponding hillslope profiles with the elevation to river on the y axis and distance to river on the x axis for each functional group. (c) Median storage of the six functional groups.
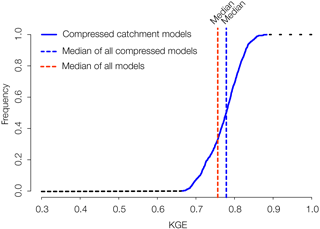
Figure 6Distribution of model performances of the different realizations of the compressed catchment model (blue). The two dashed lines correspond to the median of the KGE values of all realization of the compressed catchment model (blue) as well as to the area-weighted median of all 105 hillslope models (red).
The results presented above provide strong evidence that information theoretic concepts are powerful tools to quantify and explain the relevance of different system characteristics for distributed modeling. Following this overall result, we will start to discuss our main finding that the amount of topographic information relevant for distributed modeling is not constant but time variant. Furthermore, in a second step, we address the closely related issue that we are able to compress the ensemble of hillslope models into functionally similar groups and that a stronger compressibility implies a higher degree of functional organization in a heterogeneous environment. This discussion leads naturally to a short reflection on the advantages that concepts from information theory offer for exploring and explaining how spatial complexity and functional similarity of hydrological systems are connected. Finally, we conclude by revisiting the seeming antagonism between landscape organization (Dooge, 1986) and functional similarity (Wagener et al., 2007) against the recurring finding of heterogeneity and randomness and hence uniqueness of hydrological places (Beven, 2000) and provide an outlook on how to generalize the approach presented here.
5.1 Temporarily varying importance of topography for distributed modeling
The relevance of spatially variable but yet time-invariant topographic information on hydrological simulations was found to be strongly time dependent. The different topographic information used within the models led to complex temporal dynamics of the information content of the probability distribution of the discharge and storage simulations at a given time step. These temporal dynamics were furthermore distinctly different for the two target variables. The Shannon entropy of the discharge simulations revealed that there are alternating periods of high redundancy and of high diversity among the hillslope responses. This resulted in several local maxima and minima of the Shannon entropy in time. These maxima and minima are not easily explained by simply attributing them to high and low flow conditions (see Appendix D). For example the global maximum of 4.9 (close to the theoretical maximum of our experiment 5.8) was observed in August, when the system rapidly switched from low to high streamflow conditions in response to a strong convective rainfall event. In contrast, the Shannon entropy of storage simulation exhibited a distinctly different pattern compared to the discharge simulations with a much stronger autocorrelation, two clear identifiable maxima in winter and overall lower values of the Shannon entropy in summer.
The overall differences between the two target variables, the dynamics of the information content within the discharge and storage simulations, and hence the changing maximal compressibility of the model ensemble, highlight that the relevant topographic information for distributed modeling depends firstly on the modeling target and secondly on the time, and thus on the prevailing forcing as well as on the state of the system. In other words, spatially distributed information about topography has a time-varying impact on the model ensemble. Hence, the necessary complexity (Schoups et al., 2008) of a distributed model to capture this information is time dependent as well.
If we try to generalize and transfer this finding from the model world to a real hydrological system, keeping in mind all the issues that go along such an approach, these results imply that different landscape entities may either function similarly or dissimilarly depending on the time. Hydrological similarity can therefore, rather than being static, be a dynamic attribute that depends on the hydrological context. Interestingly, this context dependence can be straightforwardly explained by the generally dissipative nature of hydrological processes (Kleidon, 2010). Rainfall and radiation push and pull the hillslopes away from their local thermodynamic equilibrium, thereby generating internal system gradients in either potential energy or capillary binding energy. These gradients get depleted during system relaxation towards the equilibrium either through release of water from hillslopes to the stream or through recharge and capillary rise (Zehe et al., 2014). However, the generation and depletion of these gradients is controlled by a large variety of meteorological and hydrological processes interacting across a hierarchy of spatial and temporal scales (Blöschl and Sivapalan, 1995). Exactly the varying dominance of these processes, and hence the changing importance of the corresponding landscape control, is the key to understanding the time-varying relevance of different system characteristics for distributed hydrological modeling and explains the varying relevance of (in our case) topography for hydrological modeling even though topography is quasi-static on a classical hydrological timescale.
5.2 Compressibility of time series and functional similarity of hillslopes
As indicated in the section above, both of the target variables, storage and discharge, never reached the theoretical maximum value of the Shannon entropy implying that the model ensemble was producing redundancy and thus was compressible during the entire year. Based on this general finding we came up with the idea of a compressed catchment model which was built upon a straightforward clustering of all hillslope models into functional groups of similar annual runoff behavior. This compressed model consisted in a single realization of 6 instead of 105 hillslopes, which were then randomly drawn from each functional group. It is of interest that by reducing the model ensemble to a smaller set of hillslope models we were still able to match on average the observed annual streamflow in the catchment. This result agrees with the findings of Fenicia et al. (2016), who stated that spatial variations of the geopotential are too small in this landscape to have a dominant influence on the annual runoff generation, and with the findings of a foregoing study where we show that the annual runoff dynamics of the Colpach catchment can be simulated using a single effectively compressed hillslope model (Loritz et al., 2017).
Neglecting all the issues that occur when we compare distributed model applications with spatially aggregated models (e.g., Obled et al., 1994; Beven and Freer, 2001; Pokhrel et al., 2012) our comparison of the differently strong compressed catchment models matches with the conclusion of Pokhrel and Gupta (2010) that, as long as we are not interested in the representation of the spatial distribution of hydrological fluxes or state variables, a spatially aggregated model which compresses the spatial variability of the landscape properties might be sufficient for predicting macroscopic variables (Hrachowitz and Clark, 2017b). However, as soon as our focus shifts to the representation of the spatial distribution of a hydrological process, information entropy bears the key to defining and diagnosing the minimum adequate complexity of a distributed model (Schoups et al., 2008), particularly as it could help guide an approach to reducing computational costs without losing information (in our case by a factor of almost 17.5).
However, the assessment of a meaningful compression that leads to a less redundant and yet well performing distributed model structure is not at all a straightforward exercise. This is corroborated by the strongly variable performance of the 1000 randomly generated compressions, which highlights that the individual performance depends strongly on the model realization. From this we conclude that, contrary to our assumption, not every hillslope model represents streamflow generation of a functional unit equally well, as our classification is based on mutual information between the annual discharge time series. The fact that two hillslope models may yet act differently at certain time steps explains why every random realization of the model compression performs slightly different. The second and maybe more general shortcoming is that our proposed compression is based on a fixed number of groups, inferred from the average annual entropy. As the average annual entropy of simulated streamflow reflects the annual average maximal compressibility of the discharge simulation, our choice for the number of functional groups seems legitimate as a first attempt on an annual scale. However, as shown in Fig. 4c the Shannon entropy of the discharge simulations deviates substantially from this value. This implies that our model structure is either too simple in periods where the entropy is larger than the average or redundant in periods where the entropy is smaller. A best possible compression of a distributed catchment model, defined as the one that avoids any loss of information and also avoids any redundancy (also referred as lossless compression e.g., Weijs et al., 2013b), will therefore require a time-variant number of functional groups. Such an effort to do simulations with a higher spatial model resolution in times of high spatial complexity and with a coarser spatial model resolution in times of low spatial complexity, as is for example done with different adaptive time-stepping schemes in numerical model implementations (e.g., Clark and Kavetski, 2010) or in adaptive model grid refinements (Faigle et al., 2014), points to new challenges that are not only beyond the scope of this study but likely also beyond the capabilities of most currently available model systems.
5.3 Information theoretic measures to quantify similarity
The venture to link the complexity of spatially distributed catchment characteristics to functional similarity led us naturally to the concepts of information and (physical) entropy (Davies, 1990; Ben-Naim, 2008). Similarity of runoff, or storage of hillslopes, implies that their contribution to streamflow is redundant and hence does not change the information entropy within the simulations beyond its areal share (at least as long as the timing of the routing is not dominant). Removing this redundancy means to compress (Weijs et al., 2013a) and in our specific case to aggregate hillslopes to larger similar functioning landscape elements which we called functional groups in relation to the definition of functional units by Zehe et al. (2014). Although it is evident that this partitioning of similar-acting units into larger groups does not require the use of information theory (e.g., Wood et al., 1988; Sawicz et al., 2011; Berghuijs et al., 2014), we believe that, in addition to the maybe more general assets of an information theoretic perspective on different hydrological issues (e.g., Weijs and van de Giesen, 2013, Gupta and Nearing, 2014; Ehret et al., 2014; Nearing et al., 2016), it has also major technical advantages for a variety of different tasks as shortly discussed in the following.
First, information theoretic measures like Shannon entropy and mutual information, when calculated with the same logarithmic base, share the same units, in our case bits. This facilitates the inter-comparison of the different variables, in our case storage and runoff, with respect to their diversity in the model ensemble. Furthermore, if calculated in the discrete form, a careful choice of the bin width according to the measurement error can also be interpreted as physical meaningful definition of the minimum separable difference between observations or simulations of the same state variable or flux. For instance, in this study, we used the inherent measurement errors of the soil moisture probes as well as the uncertainty in our rating curves to define the minimum separable differences of storage and runoff.
Another key advantage of the information theoretic perspective is that not only the minimum but also maximum information content and hence the maximal complexity or functional disorganization that a distributed model can produce in its responses is well defined. The latter corresponds to the state of maximum Shannon entropy which implies that each time series, either modeled or observed, contributes in a unique (non-redundant) fashion to the ensemble. We are therefore able to derive a theoretical upper and lower bound which reflects naturally the minimum and maximum reachable complexity of state and/or output response that our model can produce. The lower boundary represented by a zero entropy, corresponds to a situation where all model elements produce with respect to the corresponding observation error the same output and hence act identically. The upper boundary or maximum entropy, in our case 6.7, corresponds to a situation where all model units produce a unique output and to a situation of no redundancy at all. Given these two margins we can judge whether different model elements, in our case hillslopes, of a chosen model provide largely independent streamflow contributions.
Based on the evidence presented here, we conclude that the proposed information theoretic measures and concepts provide a powerful framework for understanding and diagnosing how landscape organization and functional similarity of hydrological systems are connected. We are aware that the specific findings of the present work are necessarily constrained by the a priori settings of the model ensemble, which exclusively focused on a spatially variable topography, while land-use, precipitation and the soil parameters were identical among the 105 hillslopes. The application of these concepts and the general mindset is, however, by no means restricted to this specific model or to topography. On the contrary, it may be generalized either by additional data sources such as land-use, bedrock topography and distributed rainfall data as well as to any ensemble of time series, modeled or observed. This opens new opportunities to systematically explore how spatial variations of different landscape characteristics and meteorological forcing affect hydrological processes. Furthermore, as we only tested first-order changes in topography and the influence on distributed modeling here, it also opens the possibility to test whether second-order effects arise from combinations of several distributed characteristics.
Finally, in line with Clark et al. (2016) we argue that a comprehensive answer to the simple question stated in the introduction – “when is the spatial variation of a system characteristic large enough that we need to account for it” – is not at all straightforward, but requires a solid theoretical framework. Following thermodynamic reasoning and information theory, the key to explain why hydrological systems often act so comprehensibly is that they are dissipative and highly organized (Zehe et al., 2014). This implies that organized simplicity might emerge when we move up to larger scales in space (Dooge, 1986; Savenije and Hrachowitz, 2017). Our results reveal, however, that simplicity manifests not only in space when moving to larger scales, but also manifests when the system moves through time as functional similarity emerges in time. We therefore propose that the concepts of landscape areas that act either similarly and are thus redundant (Wagener et al., 2007) or show unique functioning and are thus irreplaceable (Beven, 2000) are consequently not mutually exclusive. They are in fact of complementary nature, and systems operate by gradually changing to different levels of organization in which their behaviors are partly unique and partly similar.
The hydrological model CATFLOW as well as all simulation results are available from the leading author on request. For the soil moisture observations please contact Markus Weiler (University of Freiburg) or Therea Blume (GFZ Potsdam) and for the discharge observations please contact Laurent Pfister or Jean-Francois Iffly from the Luxembourg Institute of Science and Technology.
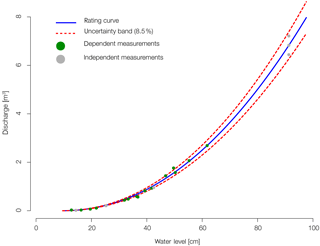
For the gauge “Colpach” the rating curve was given with
where Q is discharge (m3 s−1) and h is gauge level (m). It was derived by ordinary least square fitting to 15 direct discharge measurements (Fig. A1, green dots). Using the rating curve for flood frequency analyses would require a validation against an independent set of direct discharge measurements (grey dots). In order for us to use it as proxy for the binning width to estimate the pdfs, we calculated its overall uncertainty relative to the total set of direct discharge measurements (green and grey dots) as RMSE with a value of 8.5 % (dashed red line).
In Fig. B1 we illustrate the influence of different bin widths when calculating the Shannon entropy of our discharge simulations as a function of time. We start as already described in Sect. 3.1 with a discharge value of 0.01 mm and then progressively increase the bin width by factors ranging from 5 to 15 % in 0.05 % steps. This graph highlights that the absolute value of the Shannon entropy depends strongly on the chosen binning size. However, more important for this study is that the overall pattern of the Shannon entropy in time does not change depending on the chosen bin size.
To illustrate the performance of this metric, Fig. C1 shows a comparison of normalized mutual information to the Pearson correlation and the Euclidean distance for the following four different synthetic cases.
- a.
Linear relationship between X and Y:
- b.
Difference between two sinusoidal functions with different amplitudes:
- c.
Quadratic relationship between X and Y:
- d.
Two independent random variables X and Y.
We used equally distant bin widths of 0.05 to estimate the pdf for the calculation of the mutual information in all four cases. If we had normalized the NMI in synthetic case b with the minimum entropy of X or Y the NMI would have been 1.
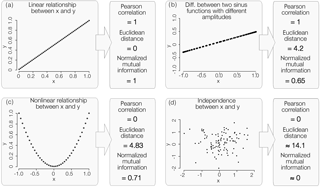
Figure C1Difference between the Pearson correlation coefficient, Euclidean distance and the normalized mutual information. Four cases are shown: (a) linear relationship, (b) the difference between two sinus functions with different amplitude, (c) a quadratic relationship and (d) two independent variables. The pdf was estimated using an equidistant bin width of 0.05 in all four cases.
Figure D1 shows the relation between the area-weighted median of the discharge simulation against the Shannon entropy of all discharge simulations for each time step. The graph highlights that there is no simple linear relation between discharge height, time of the year and the Shannon entropy.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Thermodynamics and optimality in the Earth system and its subsystems (ESD/HESS inter-journal SI)”. It is not associated with a conference.
This research contributes to the Catchments As Organized Systems (CAOS) research group (FOR 1598) funded by the German Science Foundation (DFG). Laurent Pfister and Jean-Francois Iffly from the Luxembourg Institute of Science and Technology (LIST) are acknowledged for organizing the permissions for the experiments and providing discharge data for the Colpach catchment. We also thank the whole CAOS team of phase I and II. In particular, we thank Markus Weiler (University of Freiburg), Theresa Blume (GFZ Potsdam) and Britta Kattenstroth (University of Freiburg) for providing and collecting the soil moisture data. Furthermore, we thank Nina Kiese, Leonard Bartels and Malte Neuper for their general support and time for various discussions. Finally we thank the editor Hubert Savenije as well as the two referees Steven Weijs and Ciaran Harman for their critical but very constructive comments.
The article processing charges for this open-access publication were covered
by a Research Centre of the Helmholtz Association.
The article processing charges for this open-access
publication
were covered by a Research
Centre of the Helmholtz Association.
Edited by: Hubert H. G. Savenije
Reviewed by: Steven Weijs and Ciaran Harman
Applebaum, D.: Probability and Information, 1st Edn., Cambridge University Press, Cambridge, 1996.
Arnaud, P., Bouvier, C., Cisneros, L., and Dominguez, R.: Influence of rainfall spatial variability on flood prediction, J. Hydrol., 260, 216–230, https://doi.org/10.1016/S0022-1694(01)00611-4, 2002.
Ben-Naim, A.: A Farewell to Entropy, World Scientific, https://doi.org/10.1142/6469, 2008.
Berghuijs, W. R., Sivapalan, M., Woods, R. A., and Savenije, H. H. G.: Patterns of similarity of seasonal water balances: A window into streamflow variability over a range of time scales, Water Resour. Res. 50, 5638–5661, https://doi.org/10.1002/2014WR015692, 2014.
Beven, K. J.: Changing ideas in hydrology – The case of physically-based models, J. Hydrol., 105, 157–172, https://doi.org/10.1016/0022-1694(89)90101-7, 1989.
Beven, K. J.: Uniqueness of place and process representations in hydrological modelling, Hydrol. Earth Syst. Sci., 4, 203–213, https://doi.org/10.5194/hess-4-203-2000, 2000.
Beven, K. J. and Freer, J.: Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology, J. Hydrol., 249, 11–29, https://doi.org/10.1016/S0022-1694(01)00421-8, 2001.
Beven, K. J. and Kirkby, M. J.: A physically based, variable contributing area model of basin hydrology, Hydrol. Sci. Bull., 24, 43–69, https://doi.org/10.1080/02626667909491834, 1979.
Blöschl, G. and Sivapalan, M.: Scale issues in hydrological modelling: A review, Hydrol. Process., 9, 251–290, https://doi.org/10.1002/hyp.3360090305, 1995.
Brunsell, N. A.: A multiscale information theory approach to assess spatial-temporal variability of daily precipitation, J. Hydrol., 385, 165–172, https://doi.org/10.1016/j.jhydrol.2010.02.016, 2010.
Celia, M. A., Bouloutas, E. T., and Zarba, R. L.: A general mass-conservative numerical solution for the unsaturated flow equation, Water Resour. Res., 26, 1483–1496, https://doi.org/10.1029/WR026i007p01483, 1990.
Chaubey, I., Cotter, A. S., Costello, T. A., and Soerens, T. S.: Effect of DEM data resolution on SWAT output uncertainty, Hydrol. Process., 19, 621–628, https://doi.org/10.1002/hyp.5607, 2005.
Clark, M. P. and Kavetski, D.: Ancient numerical daemons of conceptual hydrological modeling: 1. Fidelity and efficiency of time stepping schemes, Water Resour. Res., 46, W10510, https://doi.org/10.1029/2009WR008894, 2010.
Clark, M. P., Schaefli, B., Schymanski, S. J., Samaniego, L., Luce, C. H., Jackson, B. M., Freer, J. E., Arnold, J. R., Moore, R. D., Istanbulluoglu, E., and Ceola, S.: Improving the theoretical underpinnings of process-based hydrologic models, Water Resour. Res., 52, 2350–2365, https://doi.org/10.1002/2015WR017910, 2016.
Cover, T. M. and Thomas, J. A.: Elements of Information Theory, Elements of Information Theory, John Wiley & Sons, Inc., Hoboken, NJ, USA, https://doi.org/10.1002/047174882X, 2005.
Das, T., Bárdossy, A., Zehe, E., and He, Y.: Comparison of conceptual model performance using different representations of spatial variability, J. Hydrol., 356, 106–118, https://doi.org/10.1016/j.jhydrol.2008.04.008, 2008.
Davies, P.: Why is the physical world so comprehensible? Complexity, entropy, Phys. Inf., VIII, 61–71, 1990.
Dooge, J. C. I.: Looking for hydrologic laws, Water Resour. Res., 22, 46S–58S, https://doi.org/10.1029/WR022i09Sp0046S, 1986.
Ehret, U., Gupta, H. V., Sivapalan, M., Weijs, S. V., Schymanski, S. J., Blöschl, G., Gelfan, A.N., Harman, C., Kleidon, A., Bogaard, T.A., Wang, D., Wagener, T., Scherer, U., Zehe, E., Bierkens, M. F. P., Di Baldassarre, G., Parajka, J., van Beek, L. P. H., van Griensven, A., Westhoff, M. C., and Winsemius, H. C.: Advancing catchment hydrology to deal with predictions under change, Hydrol. Earth Syst. Sci., 18, 649–671, https://doi.org/10.5194/hess-18-649-2014, 2014.
Emmanuel, I., Andrieu, H., Leblois, E., Janey, N., and Payrastre, O.: Influence of rainfall spatial variability on rainfall-runoff modelling: Benefit of a simulation approach?, J. Hydrol., 531, 337–348, https://doi.org/10.1016/j.jhydrol.2015.04.058, 2015.
Faigle, B., Helmig, R., Aavatsmark, I., and Flemisch, B.: Efficient multiphysics modelling with adaptive grid refinement using a MPFA method, Comput. Geosci., 18, 625–636, https://doi.org/10.1007/s10596-014-9407-1, 2014.
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., Kobrick, M., Paller, M., Rodriguez, E., Roth, L., Seal, D., Shaffer, S., Shimada, J., Umland, J., Werner, M., Oskin, M., Burbank, D., and Alsdorf, D.: The Shuttle Radar Topography Mission, Rev. Geophys., 45, RG2004, https://doi.org/10.1029/2005RG000183, 2007.
Fenicia, F., Kavetski, D., Savenije, H. H. G., and Pfister, L.: From spatially variable streamflow to distributed hydrological models: Analysis of key modeling decisions, Water Resour. Res., 52, 954–989, https://doi.org/10.1002/2015WR017398, 2016.
Francke, T., Güntner, A., Mamede, G., Müller, E. N., and Bronstert, A.: Automated catena-based discretization of landscapes for the derivation of hydrological modelling units, Int. J. Geogr. Inf. Sci., 22, 111–132, https://doi.org/10.1080/13658810701300873, 2008.
Freeze, R. A. and Harlan, R. L.: Blueprint for a physically-based, digitally-simulated hydrologic response model, J. Hydrol., 9, 237–258, https://doi.org/10.1016/0022-1694(69)90020-1, 1969.
Gong, W., Yang, D., Gupta, H. V., and Nearing, G.: Estimating information entropy for hydrological data: One-dimensional case, Water Resour. Res., 50, 5003–5018, https://doi.org/10.1002/2014WR015874, 2014.
Gupta, H. V. and Nearing, G. S.: Debates-the future of hydrological sciences: A (common) path forward? Using models and data to learn: A systems theoretic perspective on the future of hydrological science, Water Resour. Res., 50, 5351–5359, https://doi.org/10.1002/2013WR015096, 2014.
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009.
Hastie, T., Tibshirani, R., and Friedman, J.: The Elements of Statistical Learning, 2nd Edn., Springer, New York, NY, 2009.
Hrachowitz, M. and Clark, M.: HESS Opinions: The complementary merits of top-down and bottom-up modelling philosophies in hydrology. Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2017-36, in review, 2017a.
Hrachowitz, M. and Clark, M. P.: HESS Opinions: The complementary merits of competing modelling philosophies in hydrology, Hydrol. Earth Syst. Sci., 21, 3953–3973, https://doi.org/10.5194/hess-21-3953-2017, 2017b.
Huuskonen, A., Saltikoff, E., and Holleman, I.: The Operational Weather Radar Network in Europe, B. Am. Meteorol. Soc., 95, 897–907, https://doi.org/10.1175/BAMS-D-12-00216.1, 2014.
Jackisch, C.: Linking structure and functioning of hydrological systems, PhD thesis, Repository KITopen, 171, https://doi.org/10.5445/IR/1000051494, 2015.
Jackisch, C., Angermann, L., Allroggen, N., Sprenger, M., Blume, T., Tronicke, J., and Zehe, E.: Form and function in hillslope hydrology: in situ imaging and characterization of flow-relevant structures, Hydrol. Earth Syst. Sci., 21, 3749–3775, https://doi.org/10.5194/hess-21-3749-2017, 2017.
Jaynes, E. T.: Information theory and statistical mechanics, Phys. Rev. Lett., 106, 620–630, 1957.
Kawachi, T., Maruyama, T., and Singh, V. P.: Rainfall entropy for delineation of water resources zones in Japan, J. Hydrol., 246, 36–44, https://doi.org/10.1016/S0022-1694(01)00355-9, 2001.
Kleidon, A.: A basic introduction to the thermodynamics of the Earth system far from equilibrium and maximum entropy production, Philos. T. Roy. Soc. B, 365, 1303–1315, https://doi.org/10.1098/rstb.2009.0310, 2010.
Kleidon, A., Zehe, E., Ehret, U., and Scherer, U.: Thermodynamics, maximum power, and the dynamics of preferential river flow structures at the continental scale, Hydrol. Earth Syst. Sci., 17, 225–251, https://doi.org/10.5194/hess-17-225-2013, 2013.
Kondepudi, D. and Prigogine, I.: Modern Thermodynamics, John Wiley & Sons, Ltd, Chichester, UK, https://doi.org/10.1002/9781118698723, 2014.
Lobligeois, F., Andréassian, V., Perrin, C., Tabary, P., and Loumagne, C.: When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events, Hydrol. Earth Syst. Sci., 18, 575–594, https://doi.org/10.5194/hess-18-575-2014, 2014.
Loritz, R., Hassler, S. K., Jackisch, C., Allroggen, N., van Schaik, L., Wienhöfer, J., and Zehe, E.: Picturing and modeling catchments by representative hillslopes, Hydrol. Earth Syst. Sci., 21, 1225–1249, https://doi.org/10.5194/hess-21-1225-2017, 2017.
Maurer, T.: Physikalisch begründete zeitkontinuierliche Modellierung des Wassertransports in kleinen ländlichen Einzugsgebieten, Karlsruher Institut für Technologie, Karlsruhe, 1997.
Michaels, G. S., Carr, D. B., Askenazi, M., Fuhrman, S., Wen, X., and Somogyi, R.: Cluster analysis and data visualization of large-scale gene expression data, Pac. Symp. Biocomput., 3, 42–53, 1998.
Murtagh, F. and Legendre, P.: Ward's Hierarchical Agglomerative Clustering Method: Which Algorithms Implement Ward's Criterion?, J. Classif., 31, 274–295, https://doi.org/10.1007/s00357-014-9161-z, 2014.
Musa, Z. N., Popescu, I., and Mynett, A.: A review of applications of satellite SAR, optical, altimetry and DEM data for surface water modelling, mapping and parameter estimation, Hydrol. Earth Syst. Sci., 19, 3755–3769, https://doi.org/10.5194/hess-19-3755-2015, 2015.
Nearing, G. S., Tian, Y., Gupta, H. V., Clark, M. P., Harrison, K. W., and Weijs, S. V.: A philosophical basis for hydrological uncertainty, Hydrolog. Sci. J., 61, 1666–1678, https://doi.org/10.1080/02626667.2016.1183009, 2016.
Neteler, M., Bowman, M. H., Landa, M., and Metz, M.: GRASS GIS: A multi-purpose open source GIS, Environ. Model. Softw., 31, 124–130, https://doi.org/10.1016/j.envsoft.2011.11.014, 2012.
Obled, C., Wendling, J., and Beven, K.: The sensitivity of hydrological models to spatial rainfall patterns: an evaluation using observed data, J. Hydrol., 159, 305–333, https://doi.org/10.1016/0022-1694(94)90263-1, 1994.
Oudin, L., Kay, A., Andréassian, V., and Perrin, C.: Are seemingly physically similar catchments truly hydrologically similar?, Water Resour. Res., 46, 1–15, https://doi.org/10.1029/2009WR008887, 2010.
Pechlivanidis, I. G., Jackson, B., Mcmillan, H., and Gupta, H. V.: Robust informational entropy-based descriptors of flow in catchment hydrology, Hydrolog. Sci. J., 61, 1–18, https://doi.org/10.1080/02626667.2014.983516, 2016.
Pokhrel, P. and Gupta, H. V.: On the use of spatial regularization strategies to improve calibration of distributed watershed models, Water Resour. Res., 46, 1–17, https://doi.org/10.1029/2009WR008066, 2010.
Pokhrel, P., Yilmaz, K. K., and Gupta, H. V.: Multiple-criteria calibration of a distributed watershed model using spatial regularization and response signatures, J. Hydrol., 418–419, 49–60, https://doi.org/10.1016/j.jhydrol.2008.12.004, 2012.
Refsgaard, J. C.: Parameterisation, calibration and validation of distributed hydrological models, J. Hydrol., 198, 69–97, https://doi.org/10.1016/S0022-1694(96)03329-X, 1997.
Robinson, J. S., Sivapalan, M., and Snell, J. D.: On the relative roles of hillslope processes, channel routing, and network geomorphology in the hydrologic response of natural catchments, Water Resour. Res., 31, 3089–3101, https://doi.org/10.1029/95WR01948, 1995.
Savenije, H. H. G. and Hrachowitz, M.: HESS Opinions “Catchments as meta-organisms – a new blueprint for hydrological modelling”, Hydrol. Earth Syst. Sci. 21, 1107–1116, https://doi.org/10.5194/hess-21-1107-2017, 2017.
Sawicz, K., Wagener, T., Sivapalan, M., Troch, P. A., and Carrillo, G.: Catchment classification: empirical analysis of hydrologic similarity based on catchment function in the eastern USA, Hydrol. Earth Syst. Sci., 15, 2895–2911, https://doi.org/10.5194/hess-15-2895-2011, 2011.
Schoorl, J. M., Sonneveld, M. P. W., and Veldkamp, A.: Three-dimensional landscape process modelling: the effect of DEM resolution, Earth Surf. Proc. Land., 25, 1025–1034, https://doi.org/10.1002/1096-9837(200008)25:9<1025::AID-ESP116>3.0.CO;2-Z, 2000.
Schoups, G., van de Giesen, N. C., and Savenije, H. H. G.: Model complexity control for hydrologic prediction, Water Resour. Res., 44, W00B03, https://doi.org/10.1029/2008WR006836, 2008.
Schweizer, D., Blum, P., and Butscher, C.: Uncertainty assessment in 3-D geological models of increasing complexity, Solid Earth, 8, 515–530, https://doi.org/10.5194/se-8-515-2017, 2017.
Scott, D. W.: On Optimal and Data-Based Histograms, Biometrika, 66, 605–610, https://doi.org/10.2307/2335182, 1979.
Seibert, S. P., Jackisch, C., Ehret, U., Pfister, L., and Zehe, E.: Unravelling abiotic and biotic controls on the seasonal water balance using data-driven dimensionless diagnostics, Hydrol. Earth Syst. Sci., 21, 2817–2841, https://doi.org/10.5194/hess-21-2817-2017, 2017.
Shannon, C. E.: A mathematical theory of communication, Bell Syst. Tech. J., 27, 379–423, https://doi.org/10.1145/584091.584093, 1948.
Singh, V. P.: Entropy Theory and its Application in Environmental and Water Engineering, in: Water Resources Research, John Wiley & Sons, Ltd, Chichester, UK, https://doi.org/10.1002/9781118428306, 2013.
Sivapalan, M.: Pattern, Process and Function: Elements of a Unified Theory of Hydrology at the Catchment Scale, in: Encyclopedia of Hydrological Sciences, John Wiley & Sons, Ltd, Chichester, UK, 2005.
Sivapalan, M., Blöschl, G., Zhang, L., and Vertessy, R.: Downward approach to hydrological prediction, Hydrol. Process., 17, 2101–2111, https://doi.org/10.1002/hyp.1425, 2003.
Smith, M. B., Seo, D. J., Koren, V. I., Reed, S. M., Zhang, Z., Duan, Q., Moreda, F., and Cong, S.: The distributed model intercomparison project (DMIP): Motivation and experiment design, J. Hydrol., 298, 4–26, https://doi.org/10.1016/j.jhydrol.2004.03.040, 2004.
Sørensen, R. and Seibert, J.: Effects of DEM resolution on the calculation of topographical indices: TWI and its components, J. Hydrol., 347, 79–89, https://doi.org/10.1016/j.jhydrol.2007.09.001, 2007.
Tetzlaff, D., Uhlenbrook, S., and Molnar, P.: Significance of spatial variability in precipitation for process-oriented modelling: results from two nested catchments using radar and ground station data, Hydrol. Earth Syst. Sci., 9, 29–41, https://doi.org/10.5194/hess-9-29-2005, 2005.
Thompson, J. A., Bell, J. C., and Butler, C. A.: Digital elevation model resolution: Effects on terrain attribute calculation and quantitative soil-landscape modeling, Geoderma, 100, 67–89, https://doi.org/10.1016/S0016-7061(00)00081-1, 2001.
Wagener, T. and Gupta, H. V.: Model identification for hydrological forecasting under uncertainty, Stoch. Environ. Res. Risk A., 19, 378–387, https://doi.org/10.1007/s00477-005-0006-5, 2005.
Wagener, T., Sivapalan, M., Troch, P., and Woods, R.: Catchment Classification and Hydrologic Similarity, Geogr. Compass, 1, 901–931, https://doi.org/10.1111/j.1749-8198.2007.00039.x, 2007.
Weijs, S. V. and van de Giesen, N.: An information-theoretical perspective on weighted ensemble forecasts, J. Hydrol., 498, 177–190, https://doi.org/10.1016/j.jhydrol.2013.06.033, 2013.
Weijs, S. V., Schoups, G., and Van De Giesen, N.: Why hydrological predictions should be evaluated using information theory, Hydrol. Earth Syst. Sci., 14, 2545–2558, https://doi.org/10.5194/hess-14-2545-2010, 2010.
Weijs, S. V., van de Giesen, N., and Parlange, M.: HydroZIP: How Hydrological Knowledge can Be Used to Improve Compression of Hydrological Data, Entropy, 15, 1289–1310, https://doi.org/10.3390/e15041289, 2013a.
Weijs, S. V., van de Giesen, N., and Parlange, M. B.: Data compression to define information content of hydrological time series, Hydrol. Earth Syst. Sci., 17, 3171–3187, https://doi.org/10.5194/hess-17-3171-2013, 2013b.
Wood, E. F., Sivapalan, M., Beven, K., and Band, L.: Effects of spatial variability and scale with implications to hydrologic modeling, J. Hydrol., 102, 29–47, https://doi.org/10.1016/0022-1694(88)90090-X, 1988.
Wrede, S., Fenicia, F., Martínez-Carreras, N., Juilleret, J., Hissler, C., Krein, A., Savenije, H. H. G., Uhlenbrook, S., Kavetski, D., and Pfister, L.: Towards more systematic perceptual model development: a case study using 3 Luxembourgish catchments, Hydrol. Process., 29, 2731–2750, https://doi.org/10.1002/hyp.10393, 2015.
Yakirevich, A., Pachepsky, Y. A., Gish, T. J., Guber, A. K., Kuznetsov, M. Y., Cady, R. E., and Nicholson, T. J.: Augmentation of groundwater monitoring networks using information theory and ensemble modeling with pedotransfer functions, J. Hydrol., 501, 13–24, https://doi.org/10.1016/j.jhydrol.2013.07.032, 2013.
Zehe, E., Maurer, T., Ihringer, J., and Plate, E.: Modeling water flow and mass transport in a loess catchment, Phys. Chem. Earth Pt. B, 26, 487–507, https://doi.org/10.1016/S1464-1909(01)00041-7, 2001.
Zehe, E., Becker, R., Bárdossy, A., and Plate, E.: Uncertainty of simulated catchment runoff response in the presence of threshold processes: Role of initial soil moisture and precipitation, J. Hydrol., 315, 183–202, https://doi.org/10.1016/j.jhydrol.2005.03.038, 2005.
Zehe, E., Ehret, U., Blume, T., Kleidon, A., Scherer, U., and Westhoff, M.: A thermodynamic approach to link self-organization, preferential flow and rainfall–runoff behaviour, Hydrol. Earth Syst. Sci., 17, 4297–4322, https://doi.org/10.5194/hess-17-4297-2013, 2013.
Zehe, E., Ehret, U., Pfister, L., Blume, T., Schröder, B., Westhoff, M., Jackisch, C., Schymanski, S. J., Weiler, M., Schulz, K., Allroggen, N., Tronicke, J., van Schaik, L., Dietrich, P., Scherer, U., Eccard, J., Wulfmeyer, V., and Kleidon, A.: HESS Opinions: From response units to functional units: a thermodynamic reinterpretation of the HRU concept to link spatial organization and functioning of intermediate scale catchments, Hydrol. Earth Syst. Sci., 18, 4635–4655, https://doi.org/10.5194/hess-18-4635-2014, 2014.
Zhang, W. and Montgomery, D. R.: Digital elevation model grid size, landscape representation, and hydrologic simulations, Water Resour. Res., 30, 1019–1028, https://doi.org/10.1029/93WR03553, 1994.
- Abstract
- Introduction
- Study area and model realizations
- Theoretical background, approach and methods
- Results
- Discussion
- Conclusion and outlook
- Data availability
- Appendix A: Uncertainty of the rating curve
- Appendix B: Influence of different bin widths on the Shannon entropy
- Appendix C: Comparison of the NMI
- Appendix D: Shannon entropy of the runoff simulations against the median discharge of the runoff simulations
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Abstract
- Introduction
- Study area and model realizations
- Theoretical background, approach and methods
- Results
- Discussion
- Conclusion and outlook
- Data availability
- Appendix A: Uncertainty of the rating curve
- Appendix B: Influence of different bin widths on the Shannon entropy
- Appendix C: Comparison of the NMI
- Appendix D: Shannon entropy of the runoff simulations against the median discharge of the runoff simulations
- Competing interests
- Special issue statement
- Acknowledgements
- References