The effect of climate change on the simulated streamflow of six Canadian rivers based on the CanRCM4 regional climate model

The effect of climate change on the hydro-climatology, particularly the streamflow, of six major Canadian rivers (Mackenzie, Yukon, Columbia, Fraser, Nelson, and St. Lawrence) is investigated by analyzing results from the historical and future simulations (RCP 4.5 and 8.5 scenarios) performed with the Canadian regional climate model (CanRCM4). Streamflow is obtained by routing runoff using river networks at 0.5° resolution. Of these six rivers, the Nelson and St. Lawrence are the most regulated. As a result, the streamflow at the mouth of these rivers shows very little seasonality. Additionally, the Great Lakes significantly dampen the seasonality of streamflow for the St. Lawrence River. Mean annual precipitation (P), evaporation (E), runoff (R), and temperature increase for all six river basins in both future scenarios considered here, and the increases are higher for the more fossil-fuel-intensive RCP 8.5 scenario. The only exception is the Nelson River basin, for which the simulated runoff increases are extremely small. The hydrological response of these rivers to climate warming is characterized by their existing climate states. The northerly Mackenzie and Yukon River basins show a decrease in the evaporation ratio ($E/P$) and an increase in the runoff ratio ($R/P$) since the increase in precipitation is more than enough to offset the increase in evaporation associated with increasing temperature. For the southerly Fraser and Columbia River basins, the $E/P$ ratio increases despite an increase in precipitation, and the $R/P$ ratio decreases due to an already milder climate in the northwestern Pacific region. The seasonality of simulated monthly streamflow is also more affected for the southerly Fraser and Columbia rivers than for the northerly Mackenzie and Yukon rivers as snow amounts decrease and snowmelt occurs earlier. The streamflow seasonality for the Mackenzie and Yukon rivers is still dominated by snowmelt at the end of the century, even in the RCP 8.5 scenario. The simulated streamflow regime for the Fraser and Columbia rivers shifts from a snow-dominated to a hybrid or rainfall-dominated regime towards the end of this century in the RCP 8.5 scenario. While we expect the climate change signal from CanRCM4 to be higher than that from other climate models, owing to the higher-than-average climate sensitivity of its parent global climate model, the results presented here provide a consistent overview of hydrological changes across six major Canadian river basins in response to a warmer climate.

1 Introduction

As the global population and the standard of living increase, so does the strain on freshwater resources. The natural availability of water is determined by the balance between precipitation (P) and evaporation (E) (this includes both evaporation and transpiration from plants). When precipitation exceeds evaporation, which is determined primarily by available energy, the water that does not evaporate or transpire (either at the surface or after infiltration into the soil), termed runoff (R), is carried by the rivers to the oceans. The seasonality of precipitation, its partitioning into snow and rainfall, and the seasonality of snowmelt and evaporation, all of which are determined by the climate in a given catchment or river basin, eventually determine the seasonality of runoff. As anthropogenic climate change progresses, changes in the mean annual amounts and the seasonality of these different water budget components will lead to corresponding changes in runoff (Trenberth et al., 2007). Changes in precipitation extremes are also expected to lead to corresponding changes in the extremes of streamflow. The changes in streamflow have implications for floods and power generation. While runoff is expressed in similar units to precipitation and evaporation (depth of water per unit time, e.g., mm s⁻¹ or m yr⁻¹), streamflow is the volume of water generated per unit time (e.g., m³ s⁻¹ or km³ yr⁻¹) and requires multiplication with the area over which runoff is generated. Streamflow is also routed down the river network, which introduces a time lag and attenuation of the peak runoff.

Output from climate and Earth system models (ESMs) remains the primary source of information for evaluating climate change impacts. Current approaches that rely on information generated by ESMs to obtain an estimate of how future streamflow may potentially change may be classified into two broad categories. The first approach uses simulated runoff directly from the land surface component of single or multiple climate models which may be routed downstream to obtain streamflow at the mouths of river basins and at different points along a given river network (Arora and Boer, 2001; Miller and Russell, 1992; Zhang et al., 2014). Using direct runoff output from climate models has the benefit that the calculated changes in runoff are physically consistent with the altered radiative balance of the Earth in response to increases in the concentrations of greenhouse gases (GHGs). The corresponding changes in the general circulation of the atmosphere result in the associated changes in near-surface temperature, precipitation, and the hydrological cycle. However, this approach suffers from three limitations: (1) the biases in the climate simulated by the climate model, (2) the fact that the land surface components of climate models are not calibrated for a given river basin but are rather designed to operate in a reasonably realistic way over the whole globe, and (3) the coarse resolution of global climate models (GCMs). The last limitation is partially addressed when data from finer-resolution regional climate models are used. The biases in the simulated climate do affect the simulated runoff for the current climate. Despite this, the approach can effectively capture the effects of climate change, including increased evaporative demand (Winter and Eltahir, 2012), reduced snowpack (Salathé et al., 2010; Shrestha et al., 2021a), increased winter streamflow, and earlier snowmelt-driven peak flow (Sushama et al., 2006; Poitras et al., 2011). The second approach attempts to overcome these limitations by downscaling and/or bias-correcting climate from climate models for future scenarios and uses that to drive a well-calibrated hydrological model for given catchments or river basins (Gosling et al., 2011; Ismail et al., 2020; Miller et al., 2021; Yoosefdoost et al., 2022). The second approach is more prevalent for watershed- to regional-scale impacts and adaptation studies. Given the large effort involved in downscaling and bias-correcting raw climate data from climate models, most current impact studies use downscaled and bias-corrected data put together by other groups rather than specifically doing this for their project. Recent examples include the downscaled and bias-corrected climate data for the conterminous United States (Thrasher et al., 2013) based on climate model outputs from the fifth phase of the Coupled Model Intercomparison Project (CMIP5) and statistically downscaled and bias-corrected data from five CMIP5 models, available at the global scale, tailored to the requirements of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP) (Lange, 2019). Both these data sets have found large applications in the impact and adaptation community. The processes of downscaling and bias correction are distinct, and they both have their inherent limitations. There are several examples of the limited ability of bias correction to correct and downscale variability and of the fact that bias correction can potentially cause implausible climate change signals (Maraun, 2016; Maraun et al., 2017). There are also uncertainties, substantial contradictions, and sensitivities to assumptions between the different downscaling methods (Hewitson et al., 2014).

Finally, while land surface models are typically used within the coupled framework of climate models, hydrological models are typically used as a standalone model for impact studies. While the primary output quantities from hydrological models are runoff and streamflow, land surface models output a range of water, energy, and CO₂ fluxes (Blyth et al., 2021; Fisher and Koven, 2020). The layer of air directly above the land surface, commonly referred to as the atmospheric or planetary boundary layer, is affected by surface–atmosphere exchanges of energy and water and extends upward into the atmosphere. A realistic representation of turbulent fluxes of energy and water in the planetary boundary layer is essential to the transport of moisture and energy through the atmosphere. As a result, while the calibration of hydrological models to reproduce observed streamflow is a routine exercise (Chegwidden et al., 2019; Hattermann et al., 2018; Huang et al., 2020; Hundecha et al., 2020), land surface models cannot be calibrated to reproduce a single or a small subset of quantities. This aspect of land surface versus hydrological models is also addressed briefly in Bolaños Chavarría et al. (2022). A review by Overgaard et al. (2006) also attempts to differentiate land surface models from hydrological models. In contrast to hydrological models, land surface models are expected to reproduce reasonably realistic estimates of a range of energy, water, and CO₂ fluxes over the whole globe. The philosophy behind land surface models, as they are used in the context of climate models, is that given (1) a model's structure and parameterizations; (2) the driving geophysical data for fields such as vegetation cover, soil depth, and soil texture; and (3) the driving meteorological variables, a model is expected to reproduce, in a reasonably realistic way, various components of the water, energy, and carbon cycles at the global scale. The global scale of land surface models within the framework of climate models precludes tuning of their parameters for individual grid cells or for a region (e.g., a river basin) to reproduce a small subset of model outputs.

While well-calibrated hydrological models are generally suitable for a given catchment or a river basin, their application cannot be easily extended to large-scale global or regional hydrologic modelling studies since it is typically not feasible to tune model parameters for all grid cells in a large domain. For a large region like Canada, correctly representing anthropogenic regulation using downscaled and bias-corrected climate data from an ensemble of climate models is a challenging task. As a result, this has been done for only a few selected river basins, considering only one basin at a time. In the end, both approaches have their strengths and limitations for assessing climate change impacts on hydrology and can be considered to be complementary to each other.

Future hydrologic projections using the second approach (hydrological modes driven by statistically downscaled and bias-adjusted climate models) are available for selected river basins in Canada. The results over the Prairies and British Columbia (Shrestha et al., 2021b; Sobie and Murdock, 2022) generally indicate shorter snow cover duration, earlier snowmelt, and a reduced annual maximum snow water equivalent as the climate warms. Streamflow projections across Canada generally indicate earlier snowmelt-driven peak flow, increased winter flow, and decreased summer flow (Budhathoki et al., 2022; Dibike et al., 2021; Islam et al., 2019; MacDonald et al., 2018; Shrestha et al., 2019). Annual streamflow is projected to increase, with higher increases in the northern basins (Bonsal et al., 2020; Stadnyk et al., 2021). However, these projections are based on different climate and hydrological models, downscaling methods, emission scenarios, and future periods, and no consistent set of projections is available across all major river basins of Canada.

In this study, we have used the first approach to provide a consistent set of projections across all major river basins of Canada while being cognizant of its limitations. We investigate the effect of climate change on the annual, monthly, and daily streamflow characteristics of six major Canadian rivers (Mackenzie, Yukon, Columbia, Fraser, Nelson, and St. Lawrence) using runoff outputs from simulations performed with version 4 of the Canadian Regional Climate Model (CanRCM4) (Scinocca et al., 2016). The river basins of the Yukon and Columbia rivers cover part of the United States of America as well. We used daily runoff generated from CanRCM4 for the historical period and for the two future scenarios (representative concentration pathways (RCPs) 4.5 and 8.5). The spatial resolution of runoff data from CanRCM4 is 0.22°, which is equivalent to about 12 km at 60° N (Canada lies between approximately 42 and 83° N). We then routed this runoff through river networks at 0.5° resolution to evaluate streamflow at the mouths of major Canadian rivers. The Mackenzie, Yukon, and Fraser rivers are somewhat less regulated than the heavily regulated Nelson, Columbia, and St. Lawrence rivers. The routing scheme used here does not take into account dams and reservoirs, and, therefore, the modelled streamflow represents natural streamflow. This aspect is discussed in more detail in Sect. 2.

2 Models and data

Equation (1) summarizes the water balance over a given grid cell or river basin for a given timescale:

$$\begin{array}{}\text{(1)}& P=E+R+\mathrm{\Delta }S,\end{array}$$

where ΔS is the change in water storage, including that in soil moisture, snow, and the canopy water storage. All terms are expressed in units of depth per unit time (e.g., mm yr⁻¹). When a system is in equilibrium, at annual or longer timescales, ΔS=0 and $P=E+R$. ΔS, however, may not be zero, even over long timescales, when a system is not in equilibrium, e.g., when snow is accumulating or melting consistently. We evaluated the precipitation P, evaporation E, and runoff R components of Eq. (1) simulated by CanRCM4 for each of the six river basins considered in this analysis and routed R to obtain streamflow at the river mouths.

2.1 The Canadian Regional Climate Model (CanRCM4)

CanRCM4 uses the fourth-generation Canadian atmospheric physics (CanAM4) package (von Salzen et al., 2013), which is the product of a multi-decadal program of climate model development at the Canadian Centre for Climate Modelling and Analysis (CCCma), a section within Environment and Climate Change Canada. The CanAM4 atmospheric physics package is also used in the CanESM2 (Arora et al., 2011), which contributed results to CMIP5. The difference between CanRCM4 and the CanESM2, other than the former being a regional climate model and the latter being a comprehensive global ESM, is that CanRCM4 employs the limited-area configuration of the Global Environmental Multiscale (GEM) model (Côté et al., 1998), which uses a semi-Lagrangian dynamical core for advection in the atmosphere and is developed by Environment and Climate Change Canada's Recherche en Prévision Numérique (RPN), where it is used for both global and regional numerical weather prediction. The CanESM2, on the other hand, uses a spectral dynamical core for advection in the atmosphere. CanRCM4 is driven at its boundaries with data from its parent model (CanESM2). An overview and the technical details of the coordinated global and regional climate modelling effort used to develop the CanESM2–CanRCM4 system are described in detail by Scinocca et al. (2016). Results from the model's North American 0.22° domain for a single ensemble member are primarily used here. In addition, we also used runoff from CanRCM4 0.44° resolution simulations for the North American domain because of the availability of a large ensemble (LE) of 50 members (CanRCM4 LE) (ECCC, 2018). The large-ensemble simulations allow the consideration of CanRCM4's internal variability, which is an intrinsic property of the climate system and models that is largely irreducible and could account for a large fraction of the inter-climate model spread (Deser et al., 2020). The results used here from CanRCM4 form part of its contribution to the Coordinated Regional Climate Downscaling Experiment (CORDEX) effort. The North American domain of the CanRCM uses a rotated latitude–longitude projection, with the North Pole at a latitude of 42.5° N and a longitude of 83° E as opposed to the geographic North Pole (latitude 90° N, longitude 0° E).

The land surface component in CanAM4 is the coupled CLASS-CTEM model. The physical processes are based on the Canadian Land Surface Scheme (CLASS) (Verseghy, 1991; Verseghy et al., 1993), and biogeochemical processes (which simulate vegetation as a dynamic component of the climate system) are based on the Canadian Terrestrial Ecosystem Model (CTEM) (Arora and Boer, 2003, 2005). The configuration of CLASS-CTEM used in the CanESM2 and CanRCM4 uses three soil layers with thicknesses of 0.10, 0.25, and 3.75 m. Liquid and frozen soil moisture contents and soil temperature are determined prognostically for the three soil layers. The temperature, albedo, mass, and density of a single-layer snowpack (when environmental conditions permit snow to exist) are also prognostically modelled. Surface runoff is generated in CLASS when precipitation intensity exceeds infiltration capacity and when the topsoil layer is saturated. The rainwater and snowmelt that infiltrate the soil are available for soil evaporation and transpiration. Any remaining water percolates down the soil profile and comes out at the bottom of the soil profile and is termed drainage. Combined surface runoff and drainage constitute total runoff. Like most land surface components of ESMs, CLASS does not include a groundwater representation. Surface runoff and drainage from CLASS are used as input into a large-scale river-routing scheme to route runoff and obtain streamflow at the mouth of the rivers considered in this study, as explained in the next section.

2.2 Variable-velocity routing model

The variable-velocity river-routing scheme of Arora and Boer (1999) that is implemented in the family of Canadian ESMs (CanESMs) (Arora et al., 2009, 2011; Swart et al., 2019) is used to route daily runoff from CanRCM4. This routing scheme has been implemented in various versions of the CanESMs at a spatial resolution of 2.81° since the year 2000. For this study, the routing scheme was implemented at a spatial resolution of 0.5°. The reason for using river routing at 0.5° resolution instead of scaling river networks to the 0.22° rotated latitude–longitude projection of CanRCM4's North American domain is that scaling river networks is a non-trivial and cumbersome task that cannot be fully automated (Arora and Harrison, 2007). In contrast, conservatively regridding runoff from one spatial resolution to another is a straightforward process. In addition, it has been shown that routing is not very sensitive to the spatial scale at which it is performed. Specifically, Arora et al. (2001) evaluated the Arora and Boer (1999) routing scheme together with the WATROUTE routing scheme at ∼ 350 and ∼ 25 km spatial resolutions, respectively, for the Mackenzie River basin. The two routing schemes were driven with the same runoff. Arora et al. (2001) conclude that, for the purpose of realistically modelling streamflow at the mouth of the rivers in climate models, flow routing at large spatial scales gives similar results to routing at finer spatial scales. In our study, the difference between the spatial resolution of runoff (0.22 and 0.44°) from the CanRCM4 model and routing (0.5°) is much smaller than that in the Arora et al. (2001) study. As a result, we do not expect that routing at a slightly different spatial resolution compared to runoff will lead to significant differences in the simulated streamflow. The routing scheme needs river flow directions, and these are obtained from the Total Integrating Runoff Pathways (TRIP) data set (http://hydro.iis.u-tokyo.ac.jp/~taikan/TRIPDATA/TRIPDATA.html, last access: 15 July 2023) of Oki and Sud (1998). The TRIP data are available on the regular latitude–longitude grid, with the geographic North Pole at its usual location (90° N, 0° E). Figure 1 shows the river networks at 0.5° resolution based on TRIP data, which also identify the six river basins investigated in this study. The Fraser River (identified by the light-green colour) appears to have a river mouth over land. This is because the Fraser River drains into the narrow Strait of Georgia, which is not resolved at the 0.5° resolution of the TRIP data set. In addition, the TRIP data set does not resolve any inland lakes and provides river flow directions over grid cells that are lakes. This is, in fact, helpful because it avoids discontinuities in the river network.

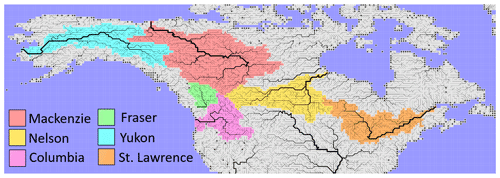
Figure 1 River flow networks used in this study at 0.5° resolution. The major river basins for which streamflow and runoff are analyzed in this study are also identified.

Figure 2 shows the schematic of the routing scheme which uses surface runoff and drainage outputs from the land surface scheme. The variable-velocity routing scheme used here is described briefly below, and more details can be found in Arora and Boer (1999). The water balance within a grid cell for its surface S (m³) and groundwater G (m³) stores is given by

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}}=f_{\mathrm{s}}+f_{\mathrm{n}}+f_{\mathrm{g}}-f_{\mathrm{o}},\text{(3)}& {\displaystyle \frac{\mathrm{d}G}{\mathrm{d}t}}=f_{\mathrm{d}}-f_{\mathrm{g}},\end{array}$$

where f_s and f_d are the surface runoff and drainage (or baseflow) estimates given by the land surface scheme; f_n and f_o are the surface water inflow from the adjacent upstream neighbouring grid cell(s) and outflow to the downstream grid cell, respectively; and f_g is the groundwater outflow from the groundwater reservoir to the surface water reservoir within a grid cell, as shown in Fig. 2. The fluxes are represented in m³ s⁻¹.

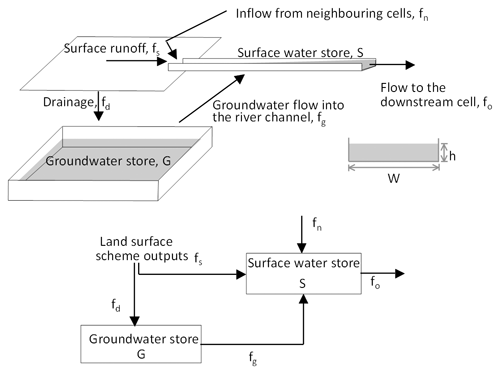
Figure 2 Schematic of the Arora and Boer (1999) river-routing scheme used in this study to route runoff simulated by CanRCM4.

A river channel is assumed to be rectangular, and the width (W) of the river at every point along the river network is specified a priori. This river width in metres is calculated based on its geomorphological relationship with mean annual discharge. The surface runoff contributes directly to the surface water store, which is essentially the amount of water in the rectangular river channel between two grid cells. The flow velocity (V, m s⁻¹) is calculated using the Manning formula (Manning, 1891):

$$\begin{array}{}\text{(4)}& V={\displaystyle \frac{\mathrm{1}}{r}}{R}^{\mathrm{2}/\mathrm{3}}{n}^{\mathrm{1}/\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{r}}{\left({\displaystyle \frac{A}{P}}\right)}^{\mathrm{2}/\mathrm{3}}{n}^{\mathrm{1}/\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{r}}{\left({\displaystyle \frac{Wh}{W+\mathrm{2}h}}\right)}^{\mathrm{2}/\mathrm{3}}{n}^{\mathrm{1}/\mathrm{2}},\end{array}$$

where r is the unitless Manning roughness coefficient (a default value of 0.04 is used), A is the area of the river channel (m²), P is the wetted perimeter (m), and h is the depth of water in the channel (m). The slope n (unitless) of the channel is calculated using elevation difference and the river length between two grid cells.

The river channel storage S is assumed to be a linear function of outflow discharge so that

$$\begin{array}{}\text{(5)}& S=\mathit{\tau }{f}_{\mathrm{o}}={\displaystyle \frac{L}{V}}AV=LA=LWh,\end{array}$$

where τ is the travel time between the grid cell under consideration and its downstream neighbour, given by $\mathit{\tau }=L/V$, where L is the distance between the grid cells (m). The outflow f_o is given by

$$\begin{array}{}\text{(6)}& f_{\mathrm{o}}=AV=WhV=Wh{\displaystyle \frac{\mathrm{1}}{r}}{\left({\displaystyle \frac{Wh}{W+\mathrm{2}h}}\right)}^{\mathrm{2}/\mathrm{3}}{n}^{\mathrm{1}/\mathrm{2}},\end{array}$$

and substituting Eqs. (5) and (6) into Eq. (2) yields

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\mathrm{d}h}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{1}}{LW}}\left(I-{\displaystyle \frac{W^{\mathrm{5}/\mathrm{3}}{h}^{\mathrm{5}/\mathrm{3}}}{r(W+\mathrm{2}h{)}^{\mathrm{2}/\mathrm{3}}}}{n}^{\mathrm{1}/\mathrm{2}}\right),\end{array}$$

where I (m³ s⁻¹) is the total inflow into a grid cell ($I=f_{\mathrm{s}}+f_{\mathrm{n}}$  + f_g). Equation (7) describes the flow in terms of the rate of change of flow depth for a given river section. An explicit forward-step finite-difference approximation for Eq. (7) yields

$$\begin{array}{}\text{(8)}& h\left(t+\mathrm{1}\right)=h\left(t\right)+{\displaystyle \frac{\mathrm{\Delta }t}{LW}}\left(I\left(t\right)-{\displaystyle \frac{W^{\mathrm{5}/\mathrm{3}}h(t{)}^{\mathrm{5}/\mathrm{3}}}{r(W+\mathrm{2}h(t){)}^{\mathrm{2}/\mathrm{3}}}}{n}^{\mathrm{1}/\mathrm{2}}\right).\end{array}$$

Flow velocity and outflow discharge for the river channel at any time step can be obtained using Eqs. (4) and (6). For the 0.5° resolution used here, a stable solution to Eq. (8) is obtained with Δt equal to around 10 min. The approach yields dynamically varying flow depth, velocity, and discharge through the river channel in response to changing surface and baseflow runoff inputs from the land surface model.

The groundwater component of the routing model assumes that groundwater storage G is a linear function of groundwater outflow f_g.

$$\begin{array}{}\text{(9)}& G={\mathit{\tau }}_{\mathrm{g}}{f}_{\mathrm{g}}\end{array}$$

The delay in groundwater storage (τ_g) is based on the dominant soil texture type and is set to 10, 35, and 65 d if the dominant soil type in each grid cell is sand, silt, and clay, respectively, following Arora and Boer (1999). Substituting G in Eq. (3) yields

$$\begin{array}{}\text{(10)}& {\mathit{\tau }}_{\mathrm{g}}{\displaystyle \frac{\mathrm{d}{f}_{\mathrm{g}}}{\mathrm{d}t}}=f_{\mathrm{d}}-f_{\mathrm{g}},\end{array}$$

and, following Arora and Boer (1999), we use the expression

$$\begin{array}{}\text{(11)}& f_{\mathrm{g}}\left(t+\mathrm{1}\right)=f_{\mathrm{g}}\left(t\right)e^{-\mathrm{\Delta }t/{\mathit{\tau }}_{\mathrm{g}}}+\left(\mathrm{1}-e^{-\frac{\mathrm{\Delta }t}{{\mathit{\tau }}_{\mathrm{g}}}}\right)f_{\mathrm{d}}\left(t\right)\end{array}$$

to determine discharge from the groundwater reservoir within a grid cell and to step forward in time, where a time step Δt equal to 3 h is used. The simplistic form of Eq. (11) allows us to use a much larger time step than the time step of 10 min required for Eq. (8).

The routing scheme used here does not consider the flow regulation effect of dams and reservoirs. However, it does consider the effect of lakes and ice jams in a simple manner. The global lake data set from Kourzeneva et al. (2012) is used, which prescribes the fractional coverage of sub-grid lakes and the five Laurentian Great Lakes (lakes Superior, Michigan, Huron, Ontario, and Erie). In particular, the flow at the mouth of the St. Lawrence River is affected significantly by the Great Lakes. The hydraulic residence time of water in the Great Lakes varies from about 2 years for Lake Erie to about 200 years for Lake Superior (Quinn, 1992). As a result, even in the absence of anthropogenic-flow regulation for the St. Lawrence River, we expect the streamflow at its mouth to show very little seasonality compared to the usual spring peak of Canadian rivers dominated by snowmelt. The simple approach used here delays the streamflow flowing into a grid cell with a lake fraction greater than 60 % using an e-folding timescale of 300 d, similarly to the treatment of the groundwater reservoir (Fig. 2) (Arora and Boer, 1999). For the St. Lawrence River, the effect of the delay caused by the Great Lakes is much larger than that of the anthropogenic-flow regulation.

Ice jams and breakups are complex thermal and mechanical events and are therefore challenging to model. They occur in all Canadian rivers to varying degrees and depend on winter temperatures, the river bathymetry, and the physical and geomorphological conditions of rivers (Beltaos, 2000; Prowse, 1986). The winter freezing of river water inevitably leads to a slow-down of river flow velocity. When water cannot move downstream, upstream flooding results. Here, we have used a simple approach that increases Manning's roughness coefficient for the Mackenzie and the Yukon rivers (which are the most northerly and are therefore affected the most by ice jams) for the period of January to June. The value of Manning's roughness coefficient is increased linearly from 0.04 to 0.08 from 1 to 31 January, kept at 0.08 from 1 February to 31 May, and then reduced linearly from 0.08 to 0.04 over the period of 1 to 30 June. Chen and She (2020) report the trend in river ice breakup dates for the Mackenzie and Yukon rivers to be around −0.3 and −1.3 d per decade for the 1950–2016 period, where the negative sign indicates that the ice breakup is occurring earlier. Assuming the same trend, the breakup dates would occur about 2.5 and 11 d earlier towards the end of this century, respectively, for the Mackenzie and Yukon rivers. This simple approach reduces the river flow velocity during the months that are most affected by river ice jams. Although this is neither a perfect nor a complete approach, this simple treatment allows us to improve the streamflow seasonality for the Mackenzie and Yukon rivers. For the southerly Fraser and Columbia rivers, such treatment was not necessary. Consideration of a higher roughness coefficient for the St. Lawrence River to account for ice jams does not affect its streamflow's seasonality (or, rather, the lack of it), which is overwhelmingly determined by the delay and storage caused by the Great Lakes.

2.3 Modelled and observation-based data

The CMIP5 historical simulation covers the period 1850–2005, and the future scenarios cover the period 2006–2100. We used the daily runoff from CanRCM4 for its 0.22° North American domain for the 20-year period from 1986–2005 based on one ensemble member of the historical simulation and for the 20-year period from 2081–2100 based on one ensemble member of each of the two future scenarios (RCP 4.5 and RCP 8.5, Moss et al., 2010). RCP 8.5 is the scenario with the highest baseline emissions, where future development is based on continuous fossil fuel development. As a result, CO₂ emissions and concentrations increase throughout the 21st century, with the CO₂ concentration around 1100 ppm in the year 2100. RCP 4.5 is a scenario of moderate emissions, in which emissions peak around 2040 and then decline: as a result, CO₂ stabilizes somewhat, reaching around 550 ppm, by the year 2100. Since CanRCM4 data are available on a rotated latitude–longitude grid and because the river routing is performed on a regular latitude–longitude grid (following the TRIP data), the runoff data from CanRCM4 are conservatively regridded to the global 0.5° grid using climate data operators (CDOs) (https://code.mpimet.mpg.de/projects/cdo/embedded/index.html#x1-7170002.12.5, last access: 10 December 2023) as mentioned earlier. These runoff data are then used as input into the routing model. The 20-year runoff data (1986–2005 for the historical simulation and 2081–2100 for the future scenarios) are concatenated into a 40-year time series for each simulation (historical, RCP 4.5, and RCP 8.5). These data are then input into the routing model, and the last 20 years of simulated streamflow is analyzed. The 20-year spin-up is sufficient to allow the surface and groundwater stores to fill up and reach equilibrium. The simulated precipitation and temperature from CanRCM4 are compared against observation-based data from the CRU TS 4.07 product (Harris et al., 2020).

The simulated streamflow is compared against observation-based estimates obtained from the Global Runoff Data Centre (GRDC) for the stations that are closest to the river mouths. Table 1 lists the drainage areas of all rivers considered in this study as discretized in the TRIP data set and at the stations closest to the river mouth. For the Columbia River, which is heavily regulated, we obtain an estimate of the naturalized flow with no regulation and no irrigation provided by the Bonville Power Administration (BPA) for the station VAN (near Vancouver, Washington, USA) (https://www.bpa.gov/energy-and-services/power/historical-streamflow-data;https://www.bpa.gov/-/media/Aep/power/historical-streamflow-reports/historic-streamflow-nrni-flows-1929-2008-corrected-04-2017.csv, last access: 15 July 2023). The drainage area of the Columbia River upstream of the VAN station is 616 960 km² and does not include discharge contributions from three tributaries (Willamette, Cowlitz, and Lewis rivers). Of these three tributaries, the contribution from Willamette is the largest. We also obtained naturalized streamflow for the Willamette River at the station SVN (drainage area of 25 600 km²) from the BPA's website (https://www.bpa.gov/-/media/Aep/power/historical-streamflow-reports/correction-20220801.zip, last access: 15 July 2023, from the file SVN6ARF_daily_COR.xlsx) and added it to the naturalized streamflow at the station VAN. This yields naturalized streamflow for the entire Columbia River basin, except for the smaller Cowlitz and Lewis rivers, and represents a drainage area of 642 560 km² (see Table 1).

Table 1 Comparison of river basin areas as represented in the TRIP data set and at the gauging station closest to the river mouth for the river basins considered in this study as obtained from the GRDC.

The Nelson River is affected by two large lakes, Lake Winnipeg and Lake Manitoba, and it is also heavily regulated. It currently has five dams towards the end of its journey as it flows into Hudson Bay. There are no upstream gauging stations close to the first upstream dam. In addition, water is also diverted from Churchill to the Nelson River. We were unable to obtain naturalized flow for the Nelson River from the Manitoba hydroelectricity company. Due to anthropogenic-flow regulation on the Nelson River, the present-day streamflow shows very little seasonality (as shown later). As a result, we do not evaluate the simulated daily or monthly streamflow for the Nelson River and focus only on its mean annual value.

3 Results

3.1 Present-day precipitation, temperature, and streamflow

Figure 3 compares the geographical distributions of mean annual precipitation (left column) and temperature (right column) simulated by CanRCM4 to observation-based estimates from the CRU TS 4.07 data set (referred to as CRU from here) for the 1986–2005 period. Although the six river basins considered in this study do not cover the entire Canadian region, for completeness, the plots are shown for the whole of Canada and the region south of Canada up to 39° N to include the southern edge of the Columbia River basin. In Fig. 3, while CanRCM4 broadly simulates the geographical distribution of temperature and precipitation reasonably realistically, there are differences compared to the CRU data set. CanRCM4 generally simulates higher precipitation over Canada, more so to the west of the Rockies (Fig. 3c), compared to observations. The model simulates cooler-than-observed temperatures to the west of the Rockies and higher-than-observed temperatures to the east of the Rockies (Fig. 3f). This is likely to be related to the representation of topography in the model. The overall somewhat higher precipitation in CanRCM4 over North America is also noted by Alaya et al. (2019), who compared probable maximum precipitation (PMP) calculated using CanRCM4 data to estimates based on several reanalyses. Alaya et al. (2019) concluded that, among the three reanalyses they considered, CanRCM4 compared best with the Climate Forecast System Reanalysis of the National Centre for Environmental Prediction's (NCEP).

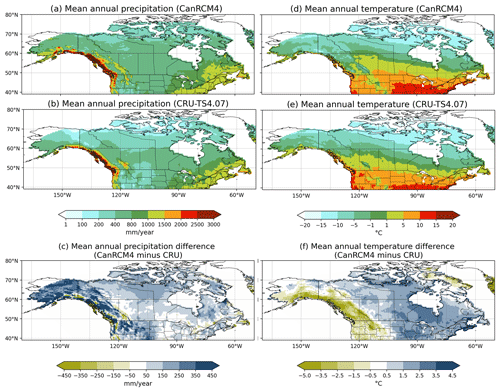
Figure 3 Comparison of CanRCM4-simulated precipitation (left column) and temperature (right column) with observation-based estimates from the CRU TS 4.07 data set for the period 1986–2005.

Figure 4 compares the simulated annual cycle of temperature (left column) and precipitation (middle column) over the six river basins (Fig. 1) selected in this study with observation-based estimates from CRU. The right-hand column compares simulated streamflow for the six river basins with observation-based estimates from the GRDC. The basin-averaged values of temperature and precipitation are calculated by area-weighting the values in the individual grid cells that lie inside a given river basin according to the TRIP data (Fig. 1). The plots also show the mean annual values (dashed lines) on the plot and their magnitude in the legend. Figure 4 shows that, overall, CanRCM4-simulated basin-wide averaged temperatures compare reasonably well with observation-based estimates based on the CRU data for the Mackenzie and the Yukon River basins. For the Columbia and Fraser, the simulated temperatures are lower for most months, and for the Nelson River basin, CanRCM4-simulated temperatures are higher compared to the CRU data. The seasonal cycle of temperature compares well with the observation-based estimates from CRU data. Compared to temperature, there are larger differences in simulated CanRCM4 precipitation compared to the CRU data. Although CanRCM4 simulates the seasonality of precipitation reasonably well compared to the CRU data, simulated precipitation is higher for all river basins, consistently with Fig. 3c. The comparison with the CRU data provides useful insights into simulated quantities. Specifically, despite the difference in the magnitudes, CanRCM4 provides a reasonable representation of the seasonality of precipitation: for example, higher winter precipitation in the southern Fraser and Columbia basins and higher summer precipitation in the northern Mackenzie and Yukon basins. However, all observation-based data sets (including CRU) have their limitations. Wong et al. (2017) compared several gridded observation-based precipitation data sets over Canada and found that they all have limitations and that the data sets compared best with gauge-based precipitation data in summer, followed by fall, spring, and winter in order of decreasing quality. Sun et al. (2018) compare global precipitation from 22 gauge-, satellite-, and reanalysis-based products, including CRU, and quantify the uncertainty in the different precipitation estimates over timescales ranging from daily to annual. Shi et al. (2017) evaluated the CRU precipitation over large regions of China and found that CRU underestimates precipitation in that region compared to rain gauge records. Furthermore, observation-based precipitation data sets also generally tend to underrepresent total precipitation in mountainous western Canada (where the Yukon, Mackenzie, Fraser, and Columbia River basins are located) due to low station density at high elevations (Werner et al., 2019). In the end, the objective of the comparison of the simulated climate with CRU observations is to evaluate whether the model climate is reasonably realistic for the present day. The assumption behind using direct output from climate models is that, despite the biases in the simulated current climate, it is possible to deduce meaningful information about the effect of climate change using the change in simulated quantities.

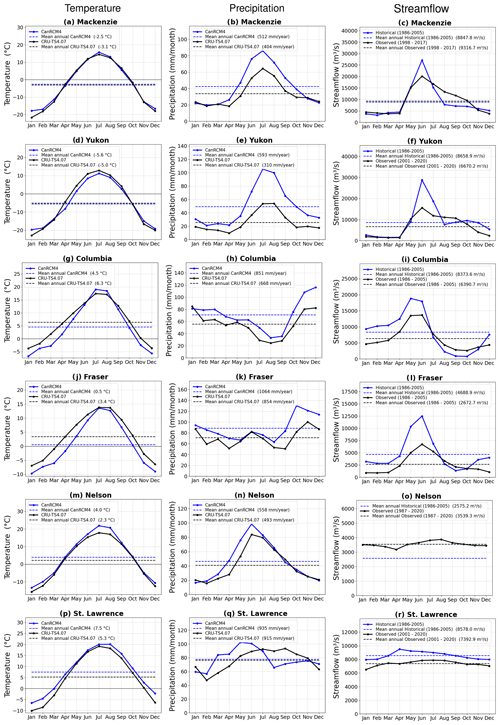
Figure 4 Comparison of the annual cycle of basin-wide averaged CanRCM4-simulated temperature (left column) and precipitation (middle column) with observation-based estimates from the CRU TS 4.07 data set for the period 1986–2005. The right-hand column compares simulated streamflow with observations from the GRDC. In the absence of the consideration of anthropogenic-flow regulations for the Nelson River, only its simulated mean annual streamflow value is evaluated.

The differences in simulated climate between CanRCM4 and the observation-based climate in CRU for the present day affect simulated streamflow as expected. The simulated mean annual streamflow is higher for four out of the six river basins considered (Yukon, Columbia, Fraser, and St. Lawrence), primarily because of the higher simulated precipitation. Simulated precipitation is also higher for the Mackenzie River basin, but the mean annual simulated streamflow compares well with its observation-based estimate. Possible reasons for reasonably realistic annual simulated streamflow despite higher precipitation include biases in the CRU data set itself (e.g., underrepresentation of total annual precipitation) or higher simulated evaporation in CanRCM4 (although simulated summer temperatures compare well with the CRU data). Finally, the simulated mean annual streamflow for the Nelson River is lower than its observation-based estimate despite somewhat higher simulated precipitation than in the CRU data. The most likely reason for this is the diversion from the Churchill River into the Nelson River, which started in 1976 to increase the water flow to larger generating stations on the lower Nelson River. The Manitoba government estimates that an average of 25 % more water flows into the lower Nelson River due to the Churchill River diversion (CRD) (https://www.gov.mb.ca/sd/water/water-power/churchill/index.html, last access: 7 September 2023). The seasonality of streamflow for the Mackenzie, Yukon, and Fraser rivers is dominated by the spring snowmelt, with the peak occurring in June for both simulated and observed streamflow. The simulated streamflow for the Columbia and Fraser rivers peaks at the right time, but there is more simulated streamflow during the winter months when precipitation is also higher than observed. For the Mackenzie and Yukon rivers, although the mean annual simulated streamflow and observed streamflow are comparable, their seasonal distribution is not. The simulated streamflow peak for these rivers is higher due to the simple treatment of ice jams, which is not sufficient to hold the water in the river channel and then release it slowly as ice jams slowly dissipate in the spring and summer months, as the observed streamflow indicates. Finally, for the St. Lawrence River, there is little seasonality in observed streamflow due to the delay caused by the Great Lakes and anthropogenic-flow regulation. The lack of strong seasonality seen in simulated streamflow for the St. Lawrence River is caused entirely by the delay caused by the Great Lakes (Sect. 2.2).

Overall, the spatial distribution of precipitation and temperature over Canada (Fig. 3) and the seasonality of these two primary climate drivers for the river basins considered in this study (Fig. 4) compare reasonably well with observation-based estimates from the CRU data, although there are differences in the absolute magnitude of these variables. The resulting seasonality of streamflow has limitations due to four factors: (1) the biases in the driving climate from CanRCM4; (2) the biases in the land surface component of CanRCM4, which partitions precipitation into evaporation and runoff; (3) the lack of calibration of the land surface component in relation to specific river basins; and (4) the lack of processes in the routing component, including the limitation of not being able to treat ice jams comprehensively. Despite these limitations, the simulated streamflow captures the broad seasonal patterns with higher values during the spring snowmelt and lower values during the winter months, as observations show.

3.2 Changes in future climate and streamflow

Figures 5, 6, and 7 show the changes in CanRCM4-simulated precipitation, temperature, and runoff for the period 2081–2100 for both RCP 4.5 and 8.5 scenarios compared to the 1986–2005 period from the historical simulation. Over Canada, simulated precipitation and temperature increase almost everywhere and in both scenarios. As expected, the magnitude of precipitation and temperature change is higher for the RCP 8.5 scenario than for the RCP 4.5 scenario. Simulated precipitation increases are higher in the coastal western and eastern Canadian regions than in central and northern parts of Canada. The central Canadian region sees the lowest increase in precipitation in both scenarios. Simulated temperature increases, as expected, are higher at higher latitudes due to polar amplification of the temperature change associated with the snow and ice albedo feedbacks. In the RCP 4.5 and 8.5 scenarios, the simulated temperature changes vary from about 3 and 6 °C, respectively, in the south, to about 6 and 11 °C, respectively, in the north. The parent climate model (CanESM2) on which CanRCM4 is based has an equilibrium climate sensitivity of 3.7 °C, somewhat on the higher side, compared to the range of 1.5 to 4.5 °C amongst climate models that contributed to CMIP5 (Schlund et al., 2020). As a result, we also expect the magnitude of simulated changes to be somewhat higher than a model with average climate sensitivity.

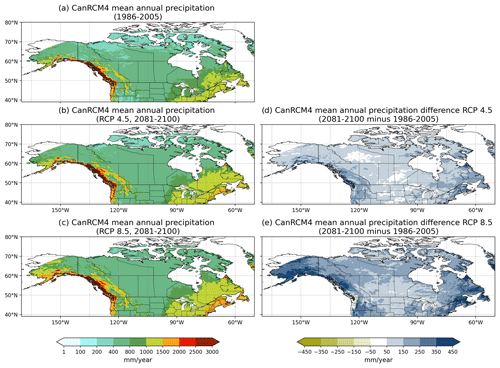
Figure 5 Comparison of CanRCM4-simulated precipitation for the 1986–2005 period for the historical scenario and for the 2081–2100 periods for the RCP 4.5 and 8.5 scenarios.

Figure 6 Comparison of CanRCM4-simulated temperature for the 1986–2005 period for the historical scenario and for the 2081–2100 periods for the RCP 4.5 and 8.5 scenarios.

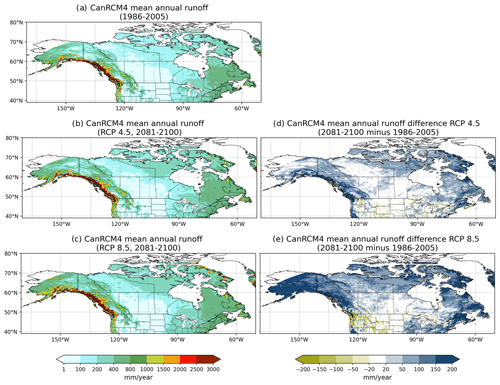
Figure 7 Comparison of CanRCM4-simulated runoff for the 1986–2005 period for the historical scenario and for the 2081–2100 periods for the RCP 4.5 and 8.5 scenarios.

In Fig. 7, runoff generally increases everywhere in Canada for the RCP 4.5 and RCP 8.5 scenarios, with larger changes on the western and eastern coasts and in northern Canada, following a similar pattern of changes in precipitation. Runoff decreases in parts of the southern Columbia River basin in the United States in the RCP 4.5 scenario, and these decreases become more pronounced and widespread over the northwestern Pacific region in the RCP 8.5 scenario, including over the Fraser River basin in Canada.

Figure 8 shows the annual cycle of the simulated water budget components (precipitation, evaporation, and runoff) for the six river basins considered in this study for the historical (1986–2005) period and the two future scenarios, RCP 4.5 and 8.5 (2081–2100). As in Fig. 4, the mean annual values are shown as dashed lines, and their magnitude is noted in the legend.

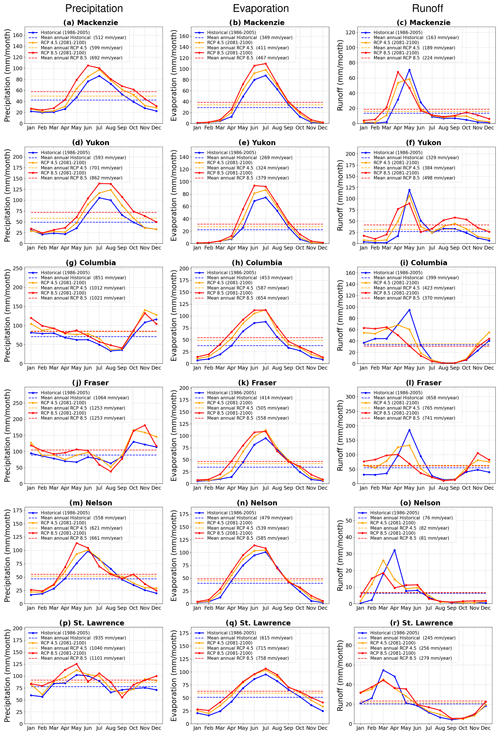
Figure 8 Comparison of the annual cycle of basin-wide averaged CanRCM4-simulated water budget components for each river basin for the historical period (1986–2005) and for the two future scenarios, RCP 4.5 and 8.5 (2081–2100): precipitation (left column), evaporation (middle column), and runoff (right column).

The evaporation ($E/P$) and runoff ($R/P$) ratios for the six river basins for the historical period and the two future scenarios are shown in Table 2 and allow us to see how the partitioning of precipitation into evaporation and runoff changes with climate. For the mean annual values of P,E, and R reported in Fig. 8, P is balanced to within 1 % by E+R for all river basins (except St. Lawrence) and all scenarios, except for the Yukon (for RCP 8.5) and Fraser River basins (for RCP 4.5 and 8.5), for which (E+R) is higher than P, indicating that ΔS is not zero (see Eq. 1). As a result, ($E/P$) and ($R/P$) also add up to 1 for all river basins, except for the Yukon (RCP 8.5: $(E+R)/P=\mathrm{1.02}$) and the Fraser River (RCP 4.5: $(E+R)/P=\mathrm{1.014}$; RCP 8.5: $(E+R)/P=\mathrm{1.036})$ basins. For the St. Lawrence River basin, the imbalance is around 2 % because of the presence of the Great Lakes, which had to be excluded from the river basin mask. Since basin-wide averaged calculations are done at 0.5° latitude–longitude resolution and because the actual domain of CanRCM4 is on a rotated latitude–longitude projection, this led to slightly more rounding errors for the St. Lawrence than for other river basins.

Table 2 Evaporation and runoff ratios for the six river basins simulated by CanRCM4 for the historical period (1986–2005) and the two future scenarios (RCP 4.5 and 8.5, 2081–2100). The evaporation (runoff) ratio is the ratio of mean annual evaporation (runoff) to precipitation.

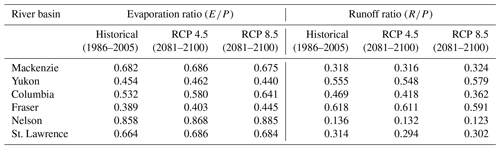
For all river basins considered, precipitation increases for both future scenarios, with the increase being larger for the RCP 8.5 scenario, consistently with Fig. 5d and e. The response of evaporation to changes in climate is expected. The increase in precipitation and temperature yields an increase in evaporation for future scenarios for all river basins. Simulated runoff does not increase as much as precipitation since evaporation also increases. The runoff ratio, as seen in Table 2, increases for the northerly Mackenzie and the Yukon River basins, while it decreases for the southerly Nelson; for the St. Lawrence; and, in particular, for the Fraser and Columbia River basins, which are characterized by a milder climate owing to their location in the northwestern Pacific region. This is because the increase in precipitation is more than enough to compensate for the increase in evaporation (associated with a warmer climate) for the northern river basins but not for the southern ones (as seen earlier in Fig. 7, where runoff begins to decrease in parts of the Columbia and Fraser River basins). The absolute runoff amount in Fig. 8 increases for the Mackenzie and Yukon River basins in the RCP 4.5 and 8.5 scenarios compared to in the historical simulation but does not change much for the Columbia, Fraser, Nelson, and St. Lawrence River basins. However, the seasonality of runoff changes for all river basins, and the peak in simulated runoff either occurs earlier in the year, occurs with reduced magnitude, or both. Canadian rivers are dominated by spring snowmelt, and this runoff behaviour is associated with snowmelt occurring earlier in the year in the RCP 4.5 scenario than in the historical simulation and occurring even earlier in the RCP 8.5. This is seen in Fig. 9, which shows the simulated annual cycle of temperature changes, snow amount, and snowfall as a fraction of total precipitation for the historical period and the two RCP scenarios for the six river basins. In Fig. 9, the mean annual temperature increases from the historical period to the RCP 4.5 scenario and from the RCP 4.5 to RCP 8.5 scenario are between 3 and 3.5 °C for the six river basins considered here. The middle column of Fig. 9 shows that, in addition to earlier snowmelt, the amount of snow in the winter months decreases for all river basins with climate warming. The only exception to this is the Yukon River basin, in which the mean annual snow amount increases marginally in the RCP 4.5 scenario (Fig. 9e). As expected, the fraction of precipitation falling as snow also decreases with climate warming for all river basins (right column, Fig. 9).

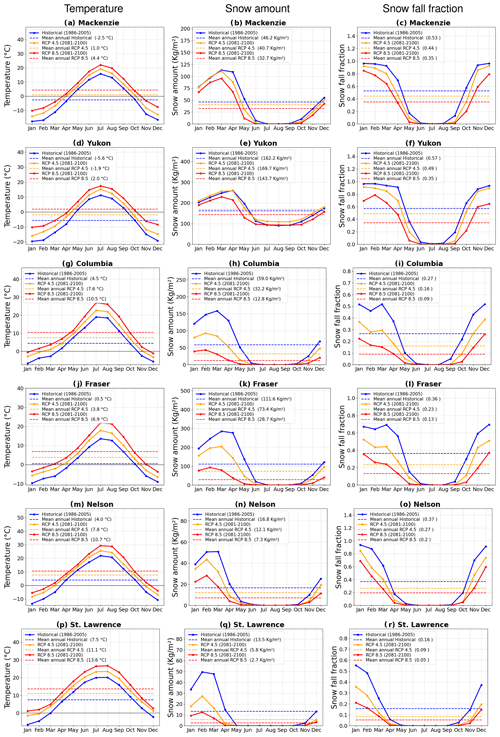
Figure 9 Comparison of the annual cycle of basin-wide averaged CanRCM4-simulated temperature (left column), snow water equivalent amount (middle column), and snowfall fraction (right column) for the historical period (1986–2005) and the two future scenarios, RCP 4.5 and 8.5 (2081–2100).

Figure 10 compares simulated daily streamflow and flow duration curves averaged over the historical period (1986–2005) with those averaged over the two future scenarios, RCP 4.5 and 8.5 (2081–2100), for the river basins considered here, excluding the Nelson River. The flow duration curves are calculated using daily streamflow values. The legends in Fig. 10 for the streamflow figures in the left column show mean annual values but also the change from the simulated historical values for the RCP 4.5 and 8.5 scenarios. The mean annual streamflow increases for all rivers in both the RCP 4.5 and 8.5 scenarios, except for the Columbia River in the RCP 8.5 scenario (−7 %). The increase in simulated annual streamflow is largest for the Mackenzie (+16 %, +39 %) and Yukon rivers (+17 %, +53 %) for the RCP 4.5 and 8.5 scenarios due to higher precipitation increases in these two basins (Fig. 8). The increase in annual streamflow for other rivers is smaller and between 6 % and 14 %. Daily streamflow and flow duration curves are not shown for the Nelson River because we do not consider anthropogenic-flow regulation, as mentioned earlier. The simulated mean annual streamflow for the Nelson River increases from 2556.6 m³ s⁻¹ (for the 1986–2005 period) to 2774.8 and 2723.8 m³ s⁻¹ for the RCP 4.5 (+9 %) and 8.5 (+7 %) scenarios, respectively (for the period 2081–2100).

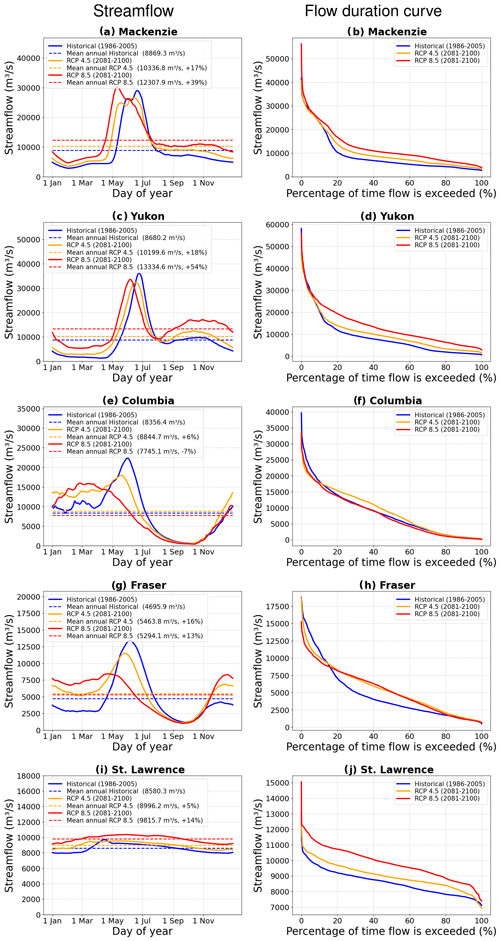
Figure 10 Comparison of the simulated daily streamflow (a, c, e, g, i) and flow duration curves (b, d, f, h, j) for the historical period (1986–2005) and the two future scenarios, RCP 4.5 and 8.5 (2081–2100), for the river basins considered. The Nelson River, for which we only evaluated annual streamflow values that are mentioned in the text, is excluded.

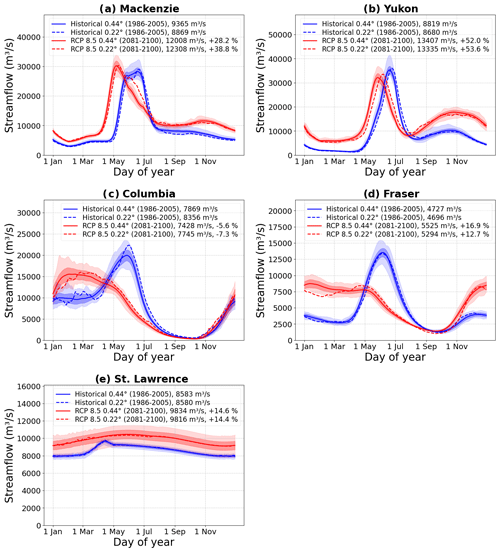
Figure 11 Comparison of the simulated daily streamflow for the historical period (1986–2005) and the RCP 8.5 scenario (2081–2100) for the river basins considered in this study from the 0.22 and 0.44° simulations. The results from the 0.22° simulations (shown earlier in Fig. 10) are shown as dashed lines. The uncertainty range for the 0.44° simulations is based on results from CanRCM4's 50-member large ensemble. The solid lines indicate the mean across 50 members, the light shading indicates the full range, and the dark shading indicates the mean ± 1 standard deviation range for the 0.44° simulations. The Nelson River, for which only annual streamflow values are analyzed, is excluded.

The changes in streamflow seasonality are larger for the southerly Columbia and Fraser rivers than for the northerly Mackenzie and Yukon rivers. The peak daily streamflow for the Yukon River still occurs in June given the fact that it is the coldest river basin (Fig. 4d), and the streamflow seasonality is still dominated by the spring snowmelt. The simulated daily peak streamflow for the Yukon River occurs on 24 June for the historical period (1986–2005) and on 18 and 6 June, respectively, for the RCP 4.5 and 8.5 scenarios for the period 2081–2100. Streamflow for the Yukon River also begins to increase earlier due to earlier snowmelt (Fig. 9e). While the spring peak streamflow decreases in both the RCP 4.5 and 8.5 scenarios during June and part of July, streamflow increases for most other months for the Yukon River. The Mackenzie River shows similar behaviour to the Yukon River in terms of earlier shifts of spring streamflow peaks with climate warming, but the spring peak is higher for the RCP 8.5 scenario. The mean simulated daily peak streamflow for the Mackenzie River occurs on 21 June for the historical period (1986–2005) and on 14 June and 11 May, respectively, for the RCP 4.5 and 8.5 scenarios for the period 2081–2100. Similarly to the Yukon, although the streamflow is lower for the Mackenzie River during June and part of July, it increases for most other months. The corresponding changes in streamflow are also seen in the flow duration curves. For these two rivers, the frequency of the occurrence of flows that occur more than about 5 % of the time in the historical simulation increases in the future. The Columbia and Fraser rivers experience much larger changes in their seasonality as their primarily snow-dominated flow regimes change to more hybrid flow regimes. The snowmelt-driven streamflow peak in spring is reduced considerably for future scenarios since a lower fraction of fall, winter, and spring precipitation falls as snow. As a result, streamflow increases from October to April since precipitation falling as rain, as opposed to snow, yields runoff that runs straight into the rivers. Additionally, the large reduction in snowpack volume together with earlier melt (Fig. 9h and k) affects the seasonality of the streamflow of the Fraser and Columbia rivers and causes pronounced shifts in peak flows. The mean simulated daily peak streamflow for the Columbia River occurs on 1 June for the historical period (1986–2005) and on 19 May and 25 February, respectively, for the RCP 4.5 and 8.5 scenarios for the period 2081–2100. For the Fraser River, the mean simulated peak streamflow occurs on 5 June for the historical period (1986–2005) and on 26 May and 21 April, respectively, for the RCP 4.5 and 8.5 scenarios for the period 2081–2100. The pronounced changes in the Fraser River basin peak flow are apparent in its flow duration curve (Fig. 10h), which shows a decrease (increase) in the frequency of streamflow events which occurred less (more) than about 16 % of the time and result in a more equitable streamflow regime, with a pronounced reduction in its seasonality. The simulated streamflow for the St. Lawrence River shows very little seasonality, and since annual streamflow increases for both scenarios, the flow duration curve simply moves up (Fig. 10j).

3.3 Uncertainty in simulated changes in future streamflow

Using the large ensemble simulations that are available for the historical period and the RCP 8.5 scenario at 0.44° resolution, we quantified the uncertainty in the simulated streamflow associated with the internal variability of CanRCM4 model. Similarly to the 0.22° resolution, we regridded the 0.44° runoff at CanRCM4's rotated latitude–longitude projection to a 0.5° regular latitude–longitude projection for use as input into the river-routing scheme. This is illustrated in Fig. 11, which shows the simulated daily streamflow for all the rivers considered here, except the Nelson River. In Fig. 11, the solid lines show the average across the 50 members of the large ensemble, light shading shows the full range of the results, and dark shading shows the mean ± 1 standard deviation range (this implies the 16 %–84 %, i.e., 68 %, range when assuming normally distributed monthly streamflow values). In addition, streamflow from the 0.22° simulations (from Fig. 10) is shown as dashed lines to allow direct comparison of results from the 0.22 and 0.44° simulations.

The changes in simulated streamflow are consistent between the 0.22 and 0.44° simulations. The results from the 0.44° simulations are also notably smoother compared to the 0.22° simulations since the 0.44° results are also averaged over the 50 ensemble members in addition to the 20 years. For the most part, the results from the 0.22° simulations lie within the full range of results from the 0.44° simulations. This is expected since the driving climate at the boundaries of CanRCM4 based on the CanESM2 is the same in both resolutions. The magnitude of change from the historical to the RCP 8.5 scenario (see the legend for individual rivers) is, however, somewhat different. This is also expected because the coarser-resolution 0.44° simulations are less representative of the basin topography than the 0.22° simulations. The day of peak streamflow occurs a few days earlier in the 0.22° simulations than in the 0.44° simulations for the Mackenzie and Yukon rivers. Overall, the large ensemble from the 0.44° simulations helps to provide context for results from the 0.22° simulations.

Overall, despite the differences in the magnitude of changes, the direction and variability of change obtained from this study are generally consistent with the previous studies using basin-scale hydrologic models, driven by statistically downscaled and bias-corrected climate model data, for instance, for the Fraser River (Islam et al., 2019; Shrestha et al., 2012), the Columbia River (Schnorbus et al., 2014), and the Yukon River (Hay and McCabe, 2010). The results presented here are also comparable to the projections from global- and regional-scale hydrologic models, e.g., for the Mackenzie River basin (Krysanova et al., 2017, 2020).

4 Summary and conclusions

This study offers a consistent analysis of results across six river basins in Canada based on results from CanRCM4 model. Despite the biases in simulated present-day CanRCM4 climate and some differences in the results based on the 0.22 and 0.44° simulations, the results provide useful information about changes in simulated streamflow that is consistent with expectations of process behaviour in a warmer climate and with published studies.

Neither future precipitation values nor temperature changes are uniform across Canada. Simulated precipitation increases are higher closer to the western and eastern coasts, and simulated temperature changes are higher towards the Arctic. Similarly to precipitation, runoff changes are also higher closer to the western and eastern coasts. The changes in simulated streamflow indicate how the present-day climate state of river basins plays a role in their response to climate change. The results yield two broadly distinct responses of monthly streamflow changes to climate warming, up until the end of this century, for the northerly Mackenzie and Yukon rivers and the southerly Fraser and Columbia rivers. Despite higher future projected temperature changes in Canada's north, peak streamflow for the Mackenzie and Yukon rivers is still dominated by the spring snowmelt. This is because the present-day colder states of these river basins imply that, even after around 6–7 °C warming, the basin-wide average temperatures are cold enough to not sufficiently change their snowmelt-dominated streamflow regimes. However, changes do occur in streamflow seasonality for these two rivers. Mean peak daily streamflow occurs earlier by about 6–7 d for the Mackenzie and Yukon rivers in the RCP 4.5 scenario and by about 28 d for the Mackenzie River and by about 12 d for the Yukon River in the RCP 8.5 scenario (Fig. 10). The earlier start of the snowmelt is the primary factor for the changes in peak streamflow and its time of occurrence, while the streamflow increases during the rest of the year (except for June and part of July) are driven by an increase in precipitation. Additionally, a higher fraction of winter precipitation occurring as rainfall drives the winter streamflow increases. In contrast, the streamflow seasonality for the southerly Fraser and Columbia rivers is significantly more affected by warmer temperatures because the mean annual basin-wide temperature for these river basins is already above 0 °C for the historical period. Both these rivers experience pronounced changes in their streamflow seasonality. The peak daily streamflow for both rivers decreases considerably and occurs about 45 d earlier for the Fraser River and about 100 d earlier for the Columbia River in the RCP 8.5 scenario. These results compare reasonably to the 1–2-month-earlier peak in previous studies for the Fraser River (Islam et al., 2019; Shrestha et al., 2012) but are higher than the 2-month-earlier peak for the Columbia River (Schnorbus et al., 2014) based on results from multiple climate models. Shrestha et al. (2021a) used CanRCM4 data to evaluate snowpack response to varying degrees of warming. They found that snowpack reduction using CanRCM4-LE is higher than the that of the ensemble of results obtained by driving a hydrological model with data from other climate models (their supplementary information), consistently with the CanESM2's higher climate sensitivity. For the Nelson and the St. Lawrence rivers, which show very little seasonality, the effect of climate change is reflected in the changes in mean annual streamflow.

The results presented here also appear to show that the simulated changes in streamflow are somewhat resolution-dependent. This would be expected, especially for topography-dominated river basins. If a large ensemble of 50 members for the 0.22° resolution were also available, it would have been easier to draw firm conclusions about the effect of the spatial resolution on changes in simulated streamflow.

There are two primary limitations of the work presented here. First, we use results from only one climate model. It would have been ideal to use runoff from other regional climate models to provide an uncertainty range based on the spread across different climate models. This would have also allowed us to evaluate how the spread across models compares to the spread across the 50 members of the CanRCM4 large ensemble. Second, the results are based on direct output from the CanRCM4 climate model, and direct climate model output is biased. This limitation is tied to our methodology. The use of bias-corrected climate data inevitably implies using a different hydrological model or land surface scheme than the land surface component of CanRCM4 and forcing it with bias-corrected climate data to obtain runoff. Finally, there are uncertainties associated with the routing process itself. As mentioned earlier, the routing scheme accounts for ice jams in a simplified manner, and anthropogenic-flow regulation is not taken into account. The implicit assumption when using raw climate model output is that, despite the biases in simulated climate, it is possible to derive useful information about the impact of climate change on the simulated streamflow and other components of the hydrological budget. The Canada-wide results presented here have allowed us to differentiate between the hydrological responses of the northerly Mackenzie and Yukon rivers and the southerly Fraser and Columbia rivers to climate change in a consistent manner. Furthermore, our results help fill the gaps in terms of regions across Canada where no climate-model-driven hydrological projections are available. Within the scope of this study, we have only evaluated streamflow at the mouth of the six major rivers considered here. The full data set of daily simulated streamflow for the 20-year historical period (1986–2005) and future periods (2081–2100) for the two scenarios based on runoff from the 0.22° simulations is made available as detailed in the “Data availability” section.

Large ensembles are now becoming more common. The challenge for similar future studies is to consider the inter-model and intra-model (based on ensemble members of the same model) spreads in the same framework to derive an uncertainty estimate that takes into account both types of uncertainties.