the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Hybrid hydrological modeling for large alpine basins: a semi-distributed approach
Bu Li
Fuqiang Tian
Mahmut Tudaji
Li Qin
Guangheng Ni
Alpine basins are important water sources for human life, and reliable hydrological modeling can enhance the water resource management in alpine basins. Recently, hybrid hydrological models, coupling process-based models and deep learning (DL), have exhibited considerable promise in hydrological simulations. However, a notable limitation of existing hybrid models lies in their failure to incorporate spatial information within the basin and describe alpine hydrological processes, which restricts their applicability in hydrological modeling in large alpine basins. To address this issue, we develop a set of hybrid semi-distributed hydrological models by employing a process-based model as the backbone and utilizing embedded neural networks (ENNs) to parameterize and replace different internal modules. The proposed models are tested on three large alpine basins on the Tibetan Plateau. A climate perturbation method is further used to test the applicability of the hybrid models to analyze the hydrological sensitivities to climate change in large alpine basins. Results indicate that proposed hybrid hydrological models can perform well in predicting runoff processes and simulating runoff component contributions in large alpine basins. The optimal hybrid model with Nash–Sutcliffe efficiencies (NSEs) higher than 0.87 shows comparable performance to state-of-the-art DL models. The hybrid model also exhibits remarkable capability in simulating hydrological processes at ungauged sites within the basin, markedly surpassing traditional distributed models. In addition, the results also show reasonable patterns in the analysis of the hydrological sensitivities to climate change. Overall, this study provides a high-performance tool enriched with explicit hydrological knowledge for hydrological prediction and improves our understanding about the hydrological sensitivities to climate change in large alpine basins.
- Article
(4830 KB) - Full-text XML
- BibTeX
- EndNote
Alpine basins are important water sources, playing a crucial role in various aspects of human life and the environment, such as domestic water supply, irrigation, hydropower generation and climate regulation (Cui et al., 2023; Huss et al., 2017; Viviroli et al., 2011). Developing reliable hydrological models is crucial for managing floods and improving water use efficiency under climate change (Blöschl et al., 2019).
Process-based hydrological models, such as EXP-Hydro (Patil and Stieglitz, 2014), CRHM (DeBeer and Pomeroy, 2017) and THREW (Nan et al., 2021), are widely used approaches for hydrological simulation in large alpine basins. These models depend on physical laws and empirical knowledge to describe physical processes and are grounded in well-defined physical mechanisms. They can be used to advance scientific understanding about the hydrological systems and provide the insight into the response of hydrological processes to climate changes (Cui et al., 2023; Li et al., 2021). However, the performance of these models is constrained by several factors, including an incomplete understanding of alpine hydrological processes, errors in the model structure and uncertainties in parameterization (Kuppel et al., 2018; Beven, 2006). These deficiencies also give rise to equifinality, making it challenging to accurately represent hydrological processes. This diminishes the credibility of process-based models in the context of climate change assessment.
Deep learning (DL) hydrological models are distinguished by their remarkable data mining capabilities, operating independently of hydrological knowledge. They have showcased exceptional model performance across diverse hydrological domains, including streamflow/discharge forecasting (Kratzert et al., 2018; Lees et al., 2021; Liu et al., 2021), snow water equivalent modeling (Duan and Ullrich, 2021) and groundwater level mapping (Solgi et al., 2021; Nourani et al., 2022). Most of these studies disregard the effect of spatial information from meteorological data on hydrological modeling. Li et al. (2023a) introduced an innovative spatiotemporal DL hydrological model, demonstrating that integrating spatial information can significantly improve the performance of DL models in hydrological modeling. Nonetheless, despite their remarkable capabilities, DL hydrological models still face scrutiny within the hydrological modeling community, primarily due to their “black-box” nature. Furthermore, DL models rely on the assumption that the dataset's distribution during the prediction period remains consistent with that of the training period. This assumption cannot be met when using DL models to assess the effects of climate change on hydrological modeling (Nearing et al., 2021; Zhong et al., 2023).
Hybrid hydrological models that combine process-based and DL approaches are anticipated to harness their respective strengths to achieve both impressive performance and a well-defined understanding of hydrological processes (Tsai et al., 2021; Shen et al., 2023). Previous studies have introduced various hybrid model configurations and demonstrated satisfactory outcomes (Feigl et al., 2022; Frame et al., 2021; Kashinath et al., 2021; Quilty et al., 2022; Bhasme et al., 2022; Kumanlioglu and Fistikoglu, 2019; Xie et al., 2021; Lu et al., 2021), while the underlying concept in many of these hybrid models remains centered on either pure DL models or process-based models. For instance, Frame et al. (2021) utilized long short-term memory (LSTM) models as post-processors for the United States National Water Model, highlighting that integrating DL models can improve performance by rectifying errors in the outcomes of process-based models. Xie et al. (2021) introduced a physically guided LSTM model by incorporating synthetic samples during model training to capture underlying physical mechanisms. Recently, some studies attempted to implement differentiable models to facilitate a bidirectional integration between process-based models and DL models (Shen et al., 2023; Baydin et al., 2018; Höge et al., 2022). Feng et al. (2022) introduced hybrid hydrological models that integrated a lumped hydrological model HBV as the foundation and incorporated embedded neural networks (ENNs) to parameterize, enhance or replace internal components without prior training. The proposed models demonstrated comparable performance to DL models and can output untrained physical variables. Our earlier work further developed hybrid models by employing ENNs to replace the internal modules of the lumped model EXP-Hydro and systematically test the impact of replacing different internal modules with ENNs (Li et al., 2023b). The findings suggest that substituting any internal component with ENNs can enhance model performance, but increasing the number of internal component replacements does not guarantee improved outcomes. Achieving optimal performance requires a delicate equilibrium between the quantity of ENNs and the process constraints inherent in the process-based model. However, Feng et al. (2022) and Li et al. (2023b) have predominantly employed lumped hydrological models as the foundational framework in hybrid models. They have not adequately accounted for the spatial information of meteorological inputs and underlying surfaces within the basin, which limits their applicability in large basins. Additionally, the effectiveness of hybrid models in the Tibetan Plateau's large alpine basins, particularly in assessing hydrological sensitivities to climate change, is yet to be clearly established. Therefore, there is a need to evolve hybrid models from lumped to distributed to adequately capture the spatial information within the basin. Moreover, it is also essential to incorporate alpine hydrological processes in hybrid models for adapting them to alpine basins and evaluate the adaptability of these hybrid models in analyzing the hydrological sensitivities to climate change in large alpine basins.
Building upon our earlier work about hybrid lumped models (Li et al., 2023b), this study aims to propose hybrid semi-distributed models that employ a hydrological model as the backbone and employ ENNs to parameterize and replace different internal modules within the sub-basin scale. The proposed models are then comprehensively assessed across three large mountainous basins on the Tibetan Plateau. A climate perturbation method is further used to analyze the hydrological sensitivities to climate change in large alpine basins. The remainder of this paper is organized as follows: Sect. 2 outlines the proposed hybrid models, study area and data; Sect. 3 shows the evaluation results of the proposed models; Sect. 4 provides details about the hydrological sensitivities to climate change; and we conclude in Sect. 5.
2.1 Model development
This study develops hybrid semi-distributed hydrological models by integrating the process-based model and embedded neural networks (ENNs; Fig. 1). Specifically, the proposed models use a semi-distributed EXP-Hydro model as the backbone, with ENNs parameterizing and replacing different internal modules. The differential programming framework is utilized to achieve a bidirectional integration between the process-based model and ENNs, enabling simultaneous parameter training of both entities.
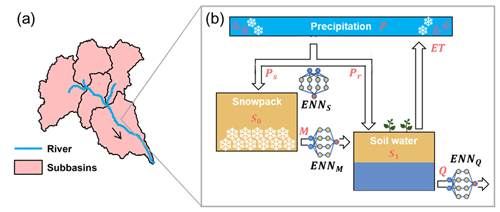
Figure 1The schematic diagram of hybrid semi-distributed models. (a) The basin is first divided into many sub-basins and (b) all meteorological and hydrological processes included in the EXP-Hydro model are calculated in each sub-basin. The precipitation partition, snowmelt and runoff modules can be optionally replaced by embedded neural networks. For detailed formulations of these processes, refer to the main text.
2.1.1 The semi-distributed EXP-Hydro model
In this study, the hybrid semi-distributed models are built upon the foundation of the semi-distributed EXP-Hydro model (Patil et al., 2014). The originally lumped EXP-Hydro model, proposed by Patil and Stieglitz (2014), treats each basin as a singular areal unit, disregarding the spatial information within the basin. The EXP-Hydro model encompasses a snow accumulation bucket and a basin bucket represented by snow storage (S0) and basin water storage (S1), respectively. Within the model, four processes are represented: precipitation partition (rainfall Pr or snowfall Ps), evapotranspiration (ET), snowmelt (M) and runoff (Q). For detailed equations, refer to Appendix A1 and Patil and Stieglitz (2014). The semi-distributed EXP-Hydro model was subsequently extended to incorporate the spatial heterogeneity within the basin (Patil et al., 2014). Initially, the study basin is divided into multiple sub-basins using a digital elevation model (DEM). The EXP-Hydro model is run independently within each sub-basin, and the overall basin runoff is derived by summing the runoff outputs from all sub-basins (Eq. A12). Patil and Stieglitz (2015) and Patil et al. (2014) showcased the efficacy of the semi-distributed EXP-Hydro model in hydrological modeling across 295 basins spanning the continental United States. Their studies indicated that this model outperforms the original EXP-Hydro model.
2.1.2 The hybrid semi-distributed models
Using the semi-distributed EXP-Hydro model as the backbone, the hybrid models integrate ENNs to parameterize and replace various internal modules within the differential programming framework (Baydin et al., 2018). This configuration enables the model to comply with basic physical principles while enhancing its representational capability of the corresponding meteorological and hydrological modules, thus increasing the accuracy of hydrological simulations. ENNs utilize both static attributes (Table A1) and dynamic meteorological time series from each sub-basin as inputs. These inputs are employed to characterize the disparities in physical mechanisms among sub-basins and to drive the precipitation–runoff processes. The hybrid models are realized via four steps:
-
Data pre-processing. A DEM is employed to partition the study basin into multiple sub-basins, guided by a drainage area threshold (Grieve et al., 2016; Noël et al., 2014). The static attributes (Table A1) and daily meteorological time series for each sub-basin are derived by calculating the areal averages from the original dataset.
-
Semi-distributed model development within the differential programming framework. All equations within the hydrological model are formulated to be differentiable to ensure operation within the differential programming framework (Shen et al., 2023; Li et al., 2023b; Levine et al., 2016). This framework facilitates the computation of derivatives from model outputs to inputs and intermediate variables, thus enabling an “end-to-end” training approach. The hybrid model achieves simultaneous training of both the semi-distributed hydrological models and ENNs. Only runoff data are employed as the training target, eliminating the need for observed data for ENN outputs. Furthermore, a physical recurrent neural network (P-RNN) is established to simulate hydrological dynamic processes and retain the memory of past basin storage sequences (Li et al., 2023b; Jiang et al., 2020).
-
ENN parameterization and replacement. The calibration parameters of all sub-basins within the basin are assumed to be the same in the semi-distributed EXP-Hydro model, while many of them related to sub-basin attributes should be different (Feng et al., 2022). To capture the spatial diversity of these calibration parameters at the sub-basin scale, we build an ENN to derive calibration parameters only using static attributes as inputs. Additionally, ENNs are employed to potentially substitute distinct internal modules of the EXP-Hydro model, utilizing static attributes and corresponding dynamic time series as inputs. Specifically, three ENNs are designed for simulating runoff, precipitation partition and snowmelt processes in this study.
-
Model training. Through the aforementioned steps, all parameters of the hybrid models, encompassing the EXP-Hydro model and ENNs, can be jointly trained using observed runoff data as the training target. The Nash–Sutcliffe efficiency (NSE; Nash and Sutcliffe, 1970) is utilized as the loss function during training.
Our previous study has shown that the utilization of ENNs to substitute internal components of lumped hydrological models can elevate model performance in hydrological modeling (Li et al., 2023b). ENNs possess the flexibility to optionally replace any single or multiple internal modules of the hydrological model. Similar to Li et al. (2023b), the ENN dedicated to precipitation partition employs precipitation and air temperature as inputs to compute the snowfall ratio. Rainfall is then determined by subtracting snowfall from the precipitation. The snowmelt ratio is determined through an ENN that takes air temperature as the input. The ENN related to the runoff process is developed using basin water storage, the combined value of rainfall and snowmelt, and air temperature as inputs. The inclusion of air temperature serves to depict the influence of soil freeze–thaw dynamics on the runoff process in alpine basins within the Tibetan Plateau (Zhong et al., 2023). Apart from the dynamic driving time series, all ENNs utilized for replacing internal components also incorporate static attributes as inputs, aiming to differentiate disparities among various sub-basins. The detailed ENNs inputs refer to Appendix B. ENNθ is used to represent the ENNs that parameterize the process-based model. ENNQ, ENNS and ENNM are utilized hereinafter to denote the ENN that replace runoff, precipitation partition and snowmelt processes, respectively.
In this study, we develop and evaluate five hybrid models denoted as DMθ, DMθ−Q, DM, DMθ−QSM and DM (Table 1). The DMθ model solely employs the ENNθ for parameterizing calibration parameters across sub-basins. The DMθ−Q and DM models go a step further by incorporating ENNQ to replace the runoff process. Expanding upon this, the precipitation partition and snowmelt processes are substituted by corresponding ENNs in DMθ−QSM and DM models. Notably, the inputs for the ENNQ include air temperature in DM and DM models, while DMθ−Q and DMθ−QSM models do not consider it.
2.1.3 Comparison models
We also compare our proposed models with the state-of-the-art distributed hydrological model THREW (Tsinghua Representative Elementary Watershed) and deep learning models LSTM and CNN-LSTM. The THREW model, originally proposed by Tian et al. (2006), operates by delineating the basin into representative elementary watersheds (REWs) through DEM calculation. Furthermore, each REW is subdivided into sub-zones, which serve as the fundamental units for hydrological modeling. The THREW model has demonstrated successful applications across diverse basins, including representative ones within the Tibetan Plateau, Alps and Tianshan (Cui et al., 2023; He et al., 2014). To establish a fair comparison of model performance between the THREW model and the proposed hybrid models, the THREW model in this study is subjected to the same spatial discretization utilized by the hybrid models. LSTM models (Hochreiter and Schmidhuber, 1997) have recently shown excellent capabilities in hydrological simulation all over the world (Kratzert et al., 2019; Lees et al., 2021; Li et al., 2023a). To benchmark against our proposed hybrid models, we have sourced the LSTM and CNN-LSTM model results from Li et al. (2023a). These models are renowned for their superior accuracy in existing deep learning research studies within the study basins. Furthermore, we also include the hybrid lumped hydrological models EXPQ and EXPQSM, proposed by Li et al. (2023b), for comparative evaluation. Their backbone model is the lumped hydrological model EXP-Hydro. This allows us to assess the effect of spatial information on hydrological modeling within hybrid frameworks. Notably, the EXPQ and EXPQSM employ the same dynamic time series inputs of ENNs for module replacement as the DM and DM models, respectively. In addition, DM and EXP are utilized hereinafter to denote semi-distributed and lumped EXP-Hydro models if not specified otherwise.
2.2 Study area and data
2.2.1 Study area
The Tibetan Plateau (TP; Fig. 2), acclaimed as the “Third Pole” and the “water tower of Asia”, stands as the world's highest plateau. The TP provides a significant source of abundant water resources, crucial for the sustenance of downstream communities. To evaluate the performance of proposed hybrid models in large alpine basins, this study focuses on the source regions of three major river basins: the Yellow River, the Yangtze River and the Lancang River. These basins are recognized as extensive mountainous regions within the TP (Fig. 2). Each of these study basins spans an area exceeding 90 000 km2, characterized by diverse topography, with elevation fluctuations exceeding 3000 m. The significant topographic variations within the basin lead to notable spatial heterogeneity in meteorological elements such as precipitation and temperature (Fig. A1). To accurately capture this heterogeneity in hydrological modeling, it is necessary to divide the basin into different computational units. In addition, previous studies have shown that the glacier process has a minimal impact on runoff modeling in the three study basins, and it is neglected in this study (Cui et al., 2023). Hereinafter, Yellow, Yangtze and Lancang are used to denote the corresponding source regions in this study.
2.2.2 Data used
This study utilized the reanalysis and remote sensing datasets for input variables of hybrid models and the THREW model as follows:
-
for precipitation, the China Meteorological Forcing Dataset (CMFD) with 0.1° spatial and 3 h temporal resolution (Yang et al., 2010);
-
the air temperature at 2 m a.g.l. (T2) from the fifth generation of ECMWF atmospheric reanalysis of the global climate (ERA5) reanalysis dataset with 0.1° spatial and 1 h temporal resolution (Hersbach et al., 2020);
-
the potential evaporation from the ERA5 reanalysis dataset with 0.1° spatial and 1 h temporal resolution (Hersbach et al., 2020);
-
for the DEM, the Shuttle Radar Topography Mission (SRTM) with 90 m spatial resolution, provided by Geospatial Data Cloud site, Computer Network Information Center, Chinese Academy of Sciences (http://www.gscloud.cn, last access: 12 May 2022);
-
for the leaf area index (LAI), the MOD15A2H dataset from MODIS product with 500 m spatial and 8 d temporal resolution (Myneni et al., 2015);
-
for the normalized difference vegetation index (NDVI), the MOD13A3 dataset from MODIS product with 1 km spatial and 1-month temporal resolution (Didan, 2015).
The daily observed runoff data at hydrological stations (Fig. 2) are used for the model calibration/training and evaluation. The dataset is provided by local water agencies.
2.3 Experimental design
2.3.1 Model evaluation schemes
We conduct two sets of experiments to comprehensively evaluate the performance of proposed hybrid semi-distributed hydrological models in this study.
-
Model performance in trained sites. All proposed hybrid semi-distributed models are developed, trained and evaluated in three study basins. The comparison models are then utilized for a range of purposes: comparing the performance of the proposed models against state-of-the-art DL and distributed hydrological models, examining the effects of ENNs parameterization and replacement on hydrological modeling, and appraising the impact of spatial information on model performance. Due to the limitation of the observed runoff data, TNH in Yellow, ZMD in Yangtze and JZ in Lancang are utilized as the evaluation stations in this experiment. For Yellow and Yangtze, the training and evaluation periods are, respectively, designated as 1982–2004 and 2007–2014. In the case of the Lancang, these periods span 1988–2003 and 2005–2010.
-
Model performance in untrained sites within the basin. By capturing the spatial heterogeneity within the basin, hybrid semi-distributed models provide the opportunity to predict hydrological processes at any untrained sites within the basin. To assess the proficiency of hybrid semi-distributed models in ungauged sites within the basin, the MT, MQ and JG stations, situated upstream of the TNH station in the Yellow (Fig. 2), are simulated using Yellow (TNH) hydrological models in this section. The evaluation phase encompasses the years 2009 to 2014 for all hydrological stations.
2.3.2 The climate perturbation method
This study uses the climate perturbation method to test the applicability of the hybrid models to analyze the hydrological sensitivities to climate change in three large alpine basins. Using precipitation and temperature data from the reanalysis dataset (Sect. 2.2.2) as the reference, the additional perturbation sequences are added to represent the potential climate changes. Perturbed precipitation sequences are extracted by multiplying the reference precipitation data from 80 % to 120 % with an increment of 10 % (Su et al., 2023). Perturbed temperature sequences are generated by adding from 0.5 to 2 °C with an increment of 0.5 °C to the reference temperature input (Cui et al., 2023). The impact of increased temperature on the potential evapotranspiration is calculated by the regression between observed temperature and potential evapotranspiration in each sub-basin (Cui et al., 2023; van Pelt et al., 2009; Xu et al., 2019). In total, one reference, four perturbed temperature and four perturbed precipitation sequences are conducted to assess the influence of precipitation and temperature change on hydrological processes. The changes of other underlying surfaces are not considered in this study.
2.3.3 Evaluation metrics
Three common hydrological metrics – including NSE, modified NSE (mNSE; Legates and McCabe , 1999) and the absolute value of peak flow bias (PFAB; Yilmaz et al., 2008) – are employed to evaluate the model performance. They can be defined as follows:
where Qobs,i and Qsim,i are the observed and simulated values, T is the length of the evaluation period, and is the averaged observed values. Qsim:l and Qobs:l are the observed and simulated runoff sorted in descending order, respectively. L is the number of flow values that are in the top 2 % of all flows. Both NSE and mNSE measure the overall goodness of fit of simulated and observed data, while mNSE gives less weight to high values than NSE and thus focuses on the baseflow. A NSE and a mNSE of 1 indicate a perfect fit, and a NSE of 0.55 is the threshold for good performance (Newman et al., 2015; Knoben et al., 2019). PFAB emphasizes the performance for peak values, and a value closer to zero indicates a smaller peak bias.
To adopt the hybrid semi-distributed models and THREW models in three basins, the Yellow, Yangtze and Lancang basins are delineated into 83, 99 and 63 sub-basins (Fig. 2) based on the actual river network and the divided sub-basin numbers in other relevant studies (Cui et al., 2023). The performance of all proposed models in gauged and ungauged sites is evaluated as follow.
3.1 Hybrid model evaluation in trained sites
3.1.1 The effect of ENNs on runoff modeling
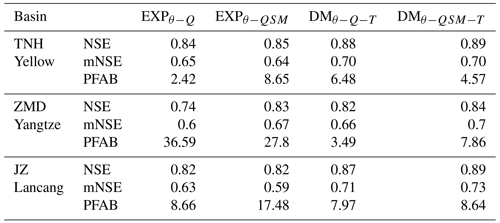
In general, all hybrid semi-distributed models exhibit notable performance, adeptly capturing the runoff peaks with appropriate magnitudes and timings across three study basins (Fig. 3 and Table 2). Specifically, the comparison results show that the DMθ model exhibits a closed but slightly better performance than the DM model in overall runoff modeling, with a slight increase in NSE and mNSE of 0.01–0.03 in all three basins. Additionally, lower PFAB results imply that the DMθ model contributes to an improved performance in peak runoff modeling. The incorporation of ENNs to represent the spatial heterogeneity of calibration parameters can reduce the peak simulation biases and slightly improve the overall performance.
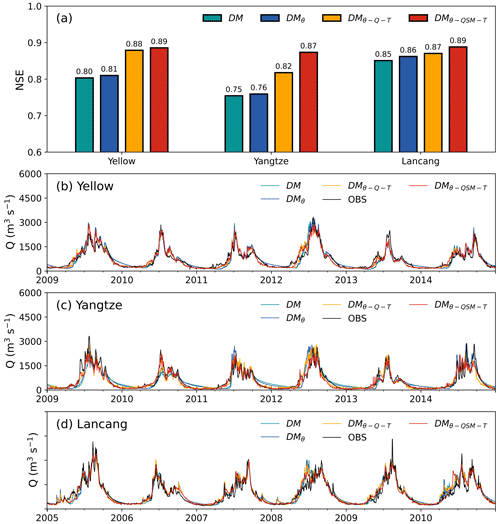
Figure 3The comparison of simulated (DM, DMθ, DM and DM models) and observed runoff processes in the evaluation period at the trained TNH, ZMD and JZ station in Yellow, Yangtze and Lancang, respectively.
Table 2The results of three hydrological metrics for different hybrid semi-distributed models in the three study basins.
The notably enhanced performance in DM and DM models indicates that the inclusion of ENNs for replacing internal modules yields further improvements in model performance (Fig. 3 and Table 2). First, the results between DM and DMθ models show the significant improvement in runoff modeling brought by the incorporation of ENNQ. This enhancement is illustrated by an increase in NSE and mNSE values, ranging from 0.06 to 0.09 in Yellow and Yangtze. Since the DMθ model already exhibits commendable performance in Lancang, the advancements achieved by the DM model are relatively marginal in comparison. PFAB results suggest that the ENNQ does not lead to substantial improvements in peak flow performance. In addition, evaluation findings for the DM model show that replacing precipitation partition and snowmelt modules by ENNs can further improve the model performance with an increase NSE of 0.01–0.05. It also does not translate into better peak runoff modeling, as evidenced by comparable PFAB scores across all three basins. ENNs employed for replacement in hybrid hydrological models have proven to be effective in enhancing the model performance in runoff modeling. Among them, the ENNQ leads to the most substantial improvements in runoff prediction performance. The replacement of ENNs for snow-related processes (ENNS and ENNM) results in comparatively minor enhancements. These findings align with our hydrological understanding as the runoff module directly generates runoff and thus plays a central role in runoff modeling. It thus contributes the most to the overall performance of runoff prediction. Conversely, the influence of snow-related processes on runoff modeling performance improvements is indirect and thus relatively modest (Li et al., 2023b).
The air temperature is employed as the additional input of the ENNQ to implicitly represent the soil freeze–thaw process in this study (Zhong et al., 2023; Gao et al., 2021). Results indicate that DM and DM models exhibit improved performance in peaking runoff modeling compared to the DMθ−Q and DMθ−QSM models, respectively. This enhancement in peaking runoff modeling is evident through closed NSE and mNSE and lower PFAB values in all three basins. Moreover, the enhancement observed due to the inclusion of air temperature is notably more pronounced in Yellow and Yangtze compared to Lancang. This pattern aligns with expectations because Lancang features a smaller extent of permafrost regions, resulting in a smaller influence of the soil freeze–thaw process on runoff modeling in this region.
3.1.2 The impact of spatial information on runoff modeling
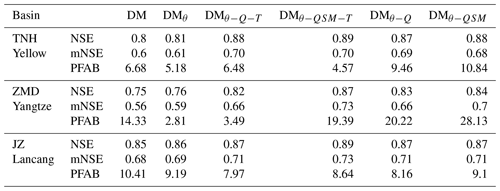
Hybrid lumped models proposed by Li et al. (2023b) are similar to our proposed hybrid semi-distributed models but did not consider the spatial heterogeneity. Hybrid lumped and semi-distributed models are used to test the effect of spatial information on hydrological modeling. It is important to highlight that while the ENNs of the hybrid lumped models utilize the same dynamic time series inputs as those of the distributed models, they do not include the static attributes of the basin. Results show that both hybrid lumped models, EXPQ and EXPQSM, exhibit strong performance in runoff modeling with NSE more than 0.74 in all three basins (Fig. 4 and Table 3). It demonstrated the suitability of hybrid lumped models for hydrological modeling on the TP. In comparison to EXPQ and EXPQSM models, the DM and DM models show more impressive performance in runoff modeling with the increase NSE and mNSE of 0.01–0.14 in three basins. PFAB results affirm that DM and DM models excel in simulating peak flow processes, achieving PFAB values of less than 10 % across all three basins. Consequently, the incorporation of spatial heterogeneity within the basin into hybrid models leads to improved performance in both overall and peak runoff modeling. This finding is seamlessly consistent with our hydrological understanding and is also corroborated by related studies in the case of distributed process-based hydrological models and DL hydrological models (Li et al., 2023a; Patil et al., 2014). In practice, we recommend the utilization of hybrid semi-distributed models for hydrological modeling, particularly in the context of large basins, to attain enhanced performance outcomes.

Figure 4(a–c) The comparison of simulated and observed runoff processes in the evaluation period in Yellow, Yangtze and Lancang, respectively. DMT and EXP are denoted to hybrid semi-distributed and lumped models, while DM represents the hybrid semi-distributed models without inclusion of air temperature in ENNQ. Circles, squares and triangles refer to NSE, mNSE and PFAB. (d) The model comparison with state-of-the-art models.
3.1.3 The comparison to the state-of-the-art models
We further use the optimal hybrid semi-distributed model DM to compare with state-of-the-art models: the distributed hydrological model THREW and the DL models LSTM and CNN-LSTM (Li et al., 2023a). Results show that the DM model outperforms the THREW model by a substantial margin and holds comparable performance to the LSTM and CNN-LSTM models (Fig. 4). This reveals that our hybrid semi-distributed model can effectively harness the advantages of both process-based models and DL models. Specifically, it attains the high performance characteristic of DL models while adhering to the physical mechanism constraints inherent in process-based models, creating a synergy not entirely realized in other models.
3.2 Hybrid semi-distributed model evaluation in untrained sites within the basin
As proposed hybrid models operate in a semi-distributed manner, it is imperative to further investigate whether models trained using the basin outlet point can effectively simulate hydrological processes in any untrained sites within the same basin. In this study, runoff processes at three hydrological stations (JG, MQ and MT), situated upstream of TNH in Yellow, are simulated using our proposed hybrid models trained by TNH data (Figs. 2 and 5).
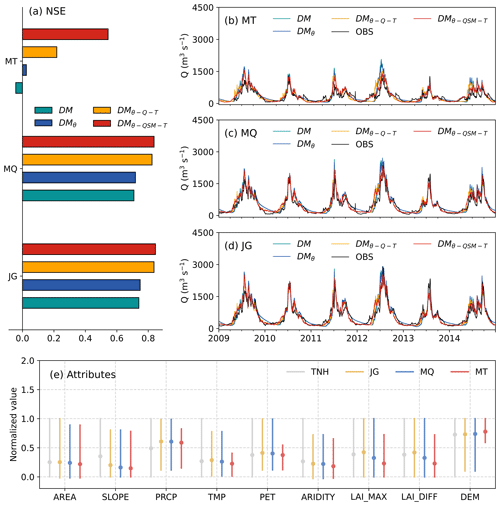
Figure 5The NSE results between simulated (different hydrological models in TNH) and observed runoff processes at JG, MQ and MT. e represents the static attributes of sub-basins normalized by the maximum–minimum in TNH.
Results reveal that all models trained on TNH data exhibit impressive performance in simulating runoff processes at JG and MQ stations, with NSE values exceeding 0.71. The DM model achieves an especially high NSE of 0.84. However, the models demonstrates lower accuracy at the station that is most upstream, MT (Fig. 2). This is because the alpine hydrological processes in the basin above the MT station, such as soil freeze–thaw and snow and ice processes, play a more significant role in runoff processes (Fig. 5e). This increases the difficulty of hydrological simulation, leading to reduced model accuracy. Among them, DM and DMθ models show the most significant reduction in accuracy due to their insufficient representation of alpine hydrological processes. On the other hand, hybrid semi-distributed models with ENN replacement, including DM and DM models, exhibit notably enhanced abilities in runoff modeling compared to DM and DMθ models, resulting in NSE improvements ranging from 0.09 to 0.58. The DM model demonstrates the strongest performance in runoff modeling across all three stations, particularly in MT where its NSE reaches 0.54, whereas the other three models yield NSE values lower than 0.22 (Fig. 5). The findings show that the proposed hybrid semi-distributed models exhibit strong performance in hydrological modeling for untrained sites within the basin. It is also demonstrated that the hydrological relationships established by ENNs are credible and robust.
Perturbed precipitation and air temperature dataset are input to trained DM models to test the applicability of the hybrid models to analyze the hydrological sensitivities to climate change in three large alpine basins.
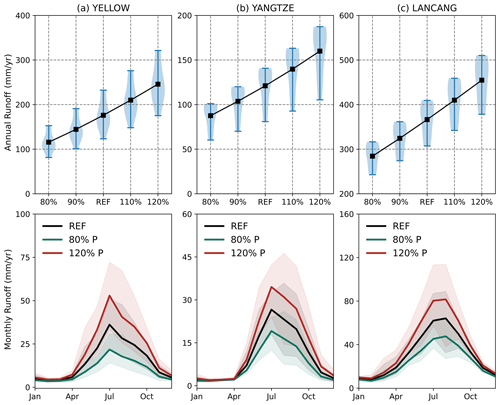
Figure 6Runoff responses to altered precipitation in the Yellow, Yangtze and Lancang basins (a–c for annual; d–f for monthly). The error bars in panels (a)–(c) and the shaded areas in panels (d)–(f) denote the range of simulated runoff.
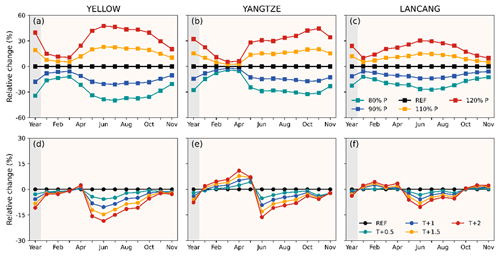
Figure 7Relative change of annual (grey background) and monthly(yellow background) runoff response to the perturbed precipitation (a–c) and air temperature (d–f) in Yellow, Yangtze and Lancang, respectively.
4.1 Sensitivities of runoff to perturbed precipitation
Figures 6 and 7a–c depict the runoff sensitivities to various altered precipitation scenarios within three study basins. The findings suggest a consistent trend in the relationship between runoff and precipitation: runoff rises (decreases) as precipitation increases (decreases). Specifically, the annual runoff increases at rates of approximately 33.8, 18.1 and 44.9 mm per 10 % with the increase of precipitation within Yellow, Yangtze and Lancang, respectively. The relative change in runoff surpasses that of precipitation in all three study basins: a 10 % increase in precipitation leads to a 15 % to 20 % increase in runoff in all three study basins. In addition, annual runoff exhibits greater sensitivity to increases in precipitation compared to decreases (Fig. 7a–c). As an illustration, an increase of 20 % in precipitation results in a substantial 40 % increase in annual runoff, whereas a 20 % decrease in precipitation leads to a notable 30 % reduction in annual runoff in Yellow. It is indicated that runoff exhibits an amplification effect in response to precipitation changes due to the increase in the runoff coefficient with rising precipitation. Figure 6a–c also illustrate that the inter-annual variation in runoff follows a pattern consistent with the annual runoff: there is a greater (lesser) variation in inter-annual runoff when there is an increase (decrease) in precipitation.

Figure 8Runoff responses to altered temperature in the Yellow, Yangtze and Lancang basins (a–c for annual; d–f for monthly). The error bars in panels (a)–(c) and the shaded areas in panels (d)–(f) denote the range of simulated runoff.
Moreover, the monthly runoff across all months shows a consistent response to perturbed precipitation, yet the extent of change varied among different months (Figs. 6d–f and 7a–c). Notably, the alterations during the wet seasons (June to October) are more pronounced compared to those in the dry seasons. This indicates that increased precipitation contributes to a more concentrated distribution of runoff. Figure 6d–f also demonstrate that intra-annual runoff variation becomes more pronounced with higher levels of precipitation. These findings can be attributed to the fact that the augmented precipitation primarily occurs during the wet seasons, and the primary runoff components during these periods consist of direct rainfall runoff.
4.2 Sensitivities of runoff to perturbed temperature
The sensitivities of runoff to changing temperature follow a more intricate pattern: runoff tends to decrease as temperatures rise. This decrease is particularly pronounced during the flood season, while in the dry season, there is a slight increase in runoff (Figs. 7d–f, 8 and 9). This shift also leads to a reduction in the intra-annual variability of runoff. Taking the temperature increase of 2 °C as an example, the annual runoff in the three study basins decreases by less than 15 %. When examining monthly runoff, the most significant increase occurs in April, while the most notable decrease is observed in June. These phenomena can be explained by the fact that changes in temperature affect the evaporation capacity, the redistribution of rainfall and snowfall, and the timing of snowmelt. Higher temperature leads to increased evaporation capability, which results in more actual evaporation and less total runoff when precipitation remains constant. During the winter and spring, the increased rainfall and earlier snowmelt, along with higher actual evaporation, tend to balance each other, resulting in a minor increase or decrease in runoff. However, in the summer, reduced snowmelt and higher evaporation significantly reduce runoff.
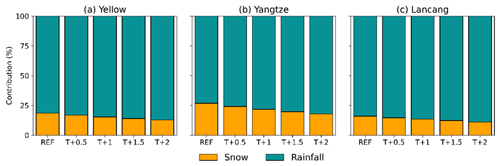
Figure 9The runoff components with different perturbed temperature scenarios in Yellow, Yangtze and Lancang, respectively.
To enhance the reliability of our model and validate our findings of hydrological sensitivities to climate change, we conducted an analysis of runoff component contributions in all three study basins across scenarios with varying temperature perturbations. It is essential to highlight that the glacier module has been excluded from this model due to structural limitations. Previous studies in the study basins have demonstrated that glaciers have a negligible impact on runoff (Cui et al., 2023; Su et al., 2023). As a result, this limitation does not significantly affect the accuracy of the simulation results. In the reference scenario, rainfall runoff emerged as the primary component, contributing approximately 81.5 %, 73.1 % and 84.0 % to the total runoff in Yellow, Yangtze and Lancang, respectively. Notably, these results align with findings from other studies (Cui et al., 2023; Su et al., 2023), underscoring that our hybrid model not only excels in simulating the runoff process but also accurately represents untrained hydrological processes. Furthermore, the contribution of snowfall runoff diminishes as the perturbed temperature increases. With a 2 °C temperature rise, the contribution of snowfall runoff decreases by 5.8 %, 8.9 % and 5.0 % in the Yellow, Yangtze and Lancang basins, respectively. These results strongly support the credibility of our analysis.
In this study, we propose hybrid semi-distributed hydrological models that synergize the semi-distributed process-based model with embedded neural networks (ENNs). The hybrid models use the semi-distributed process-based model as the backbone, with ENNs parameterizing and replacing internal modules. Taking three large alpine basins on the Tibetan Plateau as the study basins, the proposed models are tested and compared with state-of-the-art models. The climate perturbation method is further carried out to test the applicability of the hybrid models to analyze the hydrological sensitivities to climate change in large alpine basins. Our main findings are as follows:
-
The optimal hybrid semi-distributed model achieves superior performance in runoff modeling, with an NSE higher than 0.87, approaching the state-of-the-art DL models and outperforming traditional process-based models. The optimal hybrid semi-distributed model also demonstrates remarkable prowess in hydrological modeling at ungauged sites within the basin.
-
Further experiments reveal that the inclusions of ENNs for parameterizing and replacing modules can lead to higher model accuracy. Considering spatial information within the basin and introducing temperature in ENNQ to represent the soil freeze–thaw process also show enhanced predictive capabilities in hybrid models.
-
The results about hydrological sensitivities to climate change show reasonable patterns: runoff exhibits an amplification effect in response to precipitation changes, with a 10 % precipitation change resulting in a 15 %–20 % runoff change in large alpine basins. Annual runoff exhibits greater sensitivity to increases in precipitation compared to decreases. The increase in temperature enhances evaporation capacity and reduces the contributions of snowfall runoff, leading to a decrease in the total runoff and a reduction in the intra-annual variability of runoff. With a 2 °C temperature rise, the contribution of snowfall runoff decreases by 5.8 %, 8.9 % and 5.0 % in the Yellow, Yangtze and Lancang basins, respectively.
In summary, we provide an effective and easily interpretable hybrid semi-distributed hydrological model and enhance our understanding about hydrological sensitivities to climate change in large alpine basins. However, being promising in modeling hydrological processes, this study also has several limitations. First, the routing method is important for hydrological modeling, especially in large basins. The technical requirements of the differential programming framework limit the consideration of routing methods in our hybrid hydrological models. We calculate the river length from each sub-basin to the basin outlet and employ this static attribute as the inputs of ENNs to implicitly characterize the routing process within the basin. In addition, this study is limited to only using three large alpine basins on the Tibetan Plateau to evaluate proposed hybrid models due to the limitation of computational resources. Third, although numerous studies have used a climate perturbation method to calculate the response of hydrological processes to climate change, this approach has difficulty capturing the true characteristics of meteorological and hydrological changes, making it hard to validate the reasonableness of the results. In this study, we compared our findings with those of related research to demonstrate the validity of our results, thereby proving the effectiveness of our proposed coupled model in analyzing the response of hydrological processes to climate change. Future research will focus on developing hybrid distributed hydrological models, including routing processes and extending the evaluation of the hybrid model to encompass a broader range of basins.
A1 Distributed EXP-Hydro model equations
The semi-distributed EXP-Hydro model firstly delineates the basin into many sub-basins. In each sub-basin, the lumped EXP-Hydro is run independently (Eqs. A1–A12) to obtain the respective runoff. The runoff from all sub-basins is then aggregated to calculate the basin runoff (Eq. A12). The detailed equations are as follows (Patil et al., 2014).
-
Water balance is
where S0, S1, Ps, Pr, M, ET and Q are snow storage, basin water storage, snowfall, rainfall, snowmelt, evaporation and runoff, respectively.
-
Precipitation partition is
where P and T are precipitation and air temperature.
-
Snowmelt is
-
Evapotranspiration is
where PET, Lday and esat(T) represent the potential evaporation, the day length and the saturation vapor pressure.
-
Runoff and baseflow are
where Qb and Qs are the baseflow generated depending on the available storage in the basin bucket and the capacity-excess runoff generated when the basin bucket is saturated. All the above undefined variables are calibration parameters. For details, please refer to Patil and Stieglitz (2014).
-
Basin runoff is
where Qbasin is the runoff at basin outlet. Qi and Ai are the runoff and area of sub-basin i. N is the total number of sub-basins within the basin.
A2 Hybrid semi-distributed model equations
In all hybrid semi-distributed models, four ENNs are constructed to parameterize (NNθ) and replace runoff (NNQ), precipitation partition (NNS) and snowmelt processes (NNM). The detailed equations are as follows.
where θd and As represent calibration parameters and static basin attributes, respectively. For detailed static basin attributes, refer to Table A1.

Figure A1The spatial heterogeneity of precipitation and air temperature in Yellow, Yangtze and Lancang.
The hybrid model code and results are available at https://cloud.tsinghua.edu.cn/d/1bb19608a7024abfaa3e/ (Li, 20214). Other datasets are publicly available as follows: DEM (http://www.gscloud.cn/sources/details/310?pid=302, Geospatial Data Cloud Site, 2019), LAI (https://doi.org/10.5067/MODIS/MOD15A2H.006, USGS, 2024), CMFD (https://doi.org/10.11888/AtmosphericPhysics.tpe.249369.file, TPDC, 2024), NDVI (https://doi.org/10.5067/MODIS/MOD13A3.006, Didan, 2015) and ERA5 T2 (https://cds.climate.copernicus.eu/datasets, CDS, 2024). The observed runoff data and the THREW model code are not publicly available for privacy reasons.
BL conceived the idea and collected the data. BL, TS, FT and GN conducted the analysis. BL drafted the manuscript, and all authors reviewed and edited the manuscript.
At least one of the (co-)authors is a member of the editorial board of Hydrology and Earth System Sciences. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This research has been supported by the Gansu Province Science and Technology Department (grant no. 22ZD6WA043) and the National Natural Science Foundation of China (grant no. 92047301).
This paper was edited by Fabrizio Fenicia and reviewed by two anonymous referees.
Baydin, A. G., Pearlmutter, B. A., Radul, A. A., and Siskind, J. M.: Automatic differentiation in machine learning: a survey, J. March. Learn. Res., 18, 1–43, 2018. a, b
Beven, K.: A manifesto for the equifinality thesis, J. Hydrol., 320, 18–36, 2006. a
Bhasme, P., Vagadiya, J., and Bhatia, U.: Enhancing predictive skills in physically-consistent way: Physics Informed Machine Learning for hydrological processes, J. Hydrol., 615, 128618, https://doi.org/10.1016/j.jhydrol.2022.128618, 2022. a
Blöschl, G., Bierkens, M. F. P., Chambel, A., Cudennec, C., Destouni, G., Fiori, A., Kirchner, J. W., McDonnell, J. J., Savenije, H. H. G., Sivapalan, M., Stumpp, C., Toth, E., Volpi, E., Carr, G., Lupton, C., Salinas, J., Széles, B., Viglione, A., Aksoy, H., Allen, S. T., Amin, A., Andréassian, V., Arheimer, B., Aryal, S. K., Baker, V., Bardsley, E., Barendrecht, M. H., Bartosova, A., Batelaan, O., Berghuijs, W. R., Beven, K., Blume, T., Bogaard, T., Borges de Amorim, P., Böttcher, M. E., Boulet, G., Breinl, K., Brilly, M., Brocca, L., Buytaert, W., Castellarin, A., Castelletti, A., Chen, X., Chen, Y., Chen, Y., Chifflard, P., Claps, P., Clark, M. P., Collins, A. L., Croke, B., Dathe, A., David, P. C., de Barros, F. P. J., de Rooij, G., Di Baldassarre, G., Driscoll, J. M., Duethmann, D., Dwivedi, R., Eris, E., Farmer, W. H., Feiccabrino, J., Ferguson, G., Ferrari, E., Ferraris, S., Fersch, B., Finger, D., Foglia, L., Fowler, K., Gartsman, B., Gascoin, S., Gaume, E., Gelfan, A., Geris, J., Gharari, S., Gleeson, T., Glendell, M., Gonzalez Bevacqua, A., González-Dugo, M. P., Grimaldi, S., Gupta, A. B., Guse, B., Han, D., Hannah, D., Harpold, A., Haun, S., Heal, K., Helfricht, K., Herrnegger, M., Hipsey, M., Hlaváčiková, H., Hohmann, C., Holko, L., Hopkinson, C., Hrachowitz, M., Illangasekare, T. H., Inam, A., Innocente, C., Istanbulluoglu, E., Jarihani, B., Kalantari, Z., Kalvans, A., Khanal, S., Khatami, S., Kiesel, J., Kirkby, M., Knoben, W., Kochanek, K., Kohnová, S., Kolechkina, A., Krause, S., Kreamer, D., Kreibich, H., Kunstmann, H., Lange, H., Liberato, M., Lindquist, E., Link, E., Liu, J., Loucks, D., Luce, C., Mahé, G., Makarieva, O., Malard, J., Mashtayeva, S., Maskey, S., Mas-Pla, J., Mavrova-Guirguinova, M., Mazzoleni, M., Mernild, S., Misstear, B., Montanari, A., Müller-Thomy, H., Nabizadeh, A., Nardi, F., Neale, C., Nesterova, N., Nurtaev, B., Odongo, V., Panda, S., Pande, S., Pang, Z., Papacharalampous, G., Perrin, C., Pfister, L., Pimentel, R., Polo, M., Post, D., Sierra, C., Ramos, M., Renner, M., Reynolds, J., Ridolfi, E., Rigon, R., Riva, M., Robertson, D., Rosso, R., Roy, T., Sá, J., Salvadori, G., Sandells, M., Schaefli, B., Schumann, A., Scolobig, A., Seibert, J., Servat, E., Shafiei, M., Sharma, A., Sidibe, M., Sidle, R., Skaugen, T., Smith, H., Spiessl, S., Stein, L., Steinsland, I., Strasser, U., Su, B., Szolgay, J., Tarboton, D., Tauro, F., Thirel, G., Tian, F., Tong, R., Tussupova, K., Tyralis, H., Uijlenhoet, R., Beek, R., Ent, R., Ploeg, M., Loon, A., Meerveld, I., Nooijen, R., Oel, P., Vidal, J., Freyberg, J., Vorogushyn, S., Wachniew, P., Wade, A., Ward, P., Westerberg, I., White, C., Wood, E., Woods, R., Xu, Z., Yilmaz, K., and Zhang, Y.: Twenty-three unsolved problems in hydrology (UPH) – a community perspective, Hydrolog. Sci. J., 64, 1141–1158, 2019. a
CDS: Climate Data Store, https://cds.climate.copernicus.eu/datasets (last access: 14 October 2024), 2024. a
Cui, T., Li, Y., Yang, L., Nan, Y., Li, K., Tudaji, M., Hu, H., Long, D., Shahid, M., Mubeen, A., He, Z., Yong, B., Lu, H., Li, C., Ni, G., Hu, C., and Tian, F.: Non-monotonic changes in Asian Water Towers' streamflow at increasing warming levels, Nat. Commun., 14, 1176, https://doi.org/10.1038/s41467-023-36804-6, 2023. a, b, c, d, e, f, g, h, i
DeBeer, C. M. and Pomeroy, J. W.: Influence of snowpack and melt energy heterogeneity on snow cover depletion and snowmelt runoff simulation in a cold mountain environment, J. Hydrol., 553, 199–213, 2017. a
Didan, K.: MOD13A3 MODIS/Terra vegetation Indices Monthly L3 Global 1 km SIN Grid V006, NASA LP DAAC [data set], https://doi.org/10.5067/MODIS/MOD13A3.006, 2015. a, b
Duan, S. and Ullrich, P.: A comprehensive investigation of machine learning models for estimating daily snow water equivalent over the Western US, Earth and Space Science Open Archive, https://doi.org/10.1002/essoar.10509011.1, 2021. a
Feigl, M., Roesky, B., Herrnegger, M., Schulz, K., and Hayashi, M.: Learning from mistakes-Assessing the performance and uncertainty in process-based models, Hydrol. Process., 36, e14515, https://doi.org/10.1002/hyp.14515, 2022. a
Feng, D., Liu, J., Lawson, K., and Shen, C.: Differentiable, Learnable, Regionalized Process‐Based Models With Multiphysical Outputs can Approach State‐Of‐The‐Art Hydrologic Prediction Accuracy, Water Resourc. Res., 58, e2022WR032404, https://doi.org/10.1029/2022WR032404, 2022. a, b, c
Frame, J. M., Kratzert, F., Raney, A., Rahman, M., Salas, F. R., and Nearing, G. S.: Post‐Processing the National Water Model with Long Short‐Term Memory Networks for Streamflow Predictions and Model Diagnostics, J. Am. Water Resour. Assoc., 57, 885–905, 2021. a, b
Gao, H., Wang, J., Yang, Y., Pan, X., Ding, Y., and Duan, Z.: Permafrost hydrology of the Qinghai-Tibet Plateau: A review of processes and modeling, Front. Earth Sci., 8, 576838, https://doi.org/10.3389/feart.2020.576838, 2021. a
Geospatial Data Cloud Site: ASTER GDEM 30M, Geospatial Data Cloud Site [data set], http://www.gscloud.cn/sources/details/310?pid=302 (last access: 12 May 2022), 2019. a
Grieve, S. W., Mudd, S. M., and Hurst, M. D.: How long is a hillslope?, Earth Surf. Proc. Land., 41, 1039–1054, 2016. a
He, Z. H., Parajka, J., Tian, F. Q., and Blöschl, G.: Estimating degree-day factors from MODIS for snowmelt runoff modeling, Hydrol. Earth Syst. Sci., 18, 4773–4789, https://doi.org/10.5194/hess-18-4773-2014, 2014. a
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz‐Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J.: The ERA5 global reanalysis, Q. J. Roy. Meteorol. Soc., 146, 1999–2049, 2020. a, b
Hochreiter, S. and Schmidhuber, J.: Long short-term memory, Neural Comput., 9, 1735–1780, 1997. a
Höge, M., Scheidegger, A., Baity-Jesi, M., Albert, C., and Fenicia, F.: Improving hydrologic models for predictions and process understanding using neural ODEs, Hydrol. Earth Syst. Sci., 26, 5085–5102, https://doi.org/10.5194/hess-26-5085-2022, 2022. a
Huss, M., Bookhagen, B., Huggel, C., Jacobsen, D., Bradley, R. S., Clague, J. J., Vuille, M., Buytaert, W., Cayan, D. R., Greenwood, G., Mark, B. G., Milner, A. M., Weingartner, R., and Winder, M.: Toward mountains without permanent snow and ice, Earth's Future, 5, 418–435, 2017. a
Jiang, S., Zheng, Y., and Solomatine, D.: Improving AI System Awareness of Geoscience Knowledge: Symbiotic Integration of Physical Approaches and Deep Learning, Geophys. Res. Lett., 47, e2020GL088229, https://doi.org/10.1029/2020GL088229, 2020. a
Kashinath, K., Mustafa, M., Albert, A., Wu, J. L., Jiang, C., Esmaeilzadeh, S., Azizzadenesheli, K., Wang, R., Chattopadhyay, A., Singh, A., Manepalli, A., Chirila, D., Yu, R., Walters, R., White, B., Xiao, H., Tchelepi, H. A., Marcus, P., Anandkumar, A., Hassanzadeh, P., and Prabhat: Physics-informed machine learning: case studies for weather and climate modelling, Philos. T. Roy. Soc. A, 379, 20200093, https://doi.org/10.1098/rsta.2020.0093, 2021. a
Knoben, W. J. M., Freer, J. E., and Woods, R. A.: Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores, Hydrol. Earth Syst. Sci., 23, 4323–4331, https://doi.org/10.5194/hess-23-4323-2019, 2019. a
Kratzert, F., Klotz, D., Brenner, C., Schulz, K., and Herrnegger, M.: Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks, Hydrol. Earth Syst. Sci., 22, 6005–6022, https://doi.org/10.5194/hess-22-6005-2018, 2018. a
Kratzert, F., Klotz, D., Shalev, G., Klambauer, G., Hochreiter, S., and Nearing, G.: Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets, Hydrol. Earth Syst. Sci., 23, 5089–5110, https://doi.org/10.5194/hess-23-5089-2019, 2019. a
Kumanlioglu, A. A. and Fistikoglu, O.: Performance Enhancement of a Conceptual Hydrological Model by Integrating Artificial Intelligence, J. Hydrol. Eng., 24, 04019047, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001850, 2019. a
Kuppel, S., Tetzlaff, D., Maneta, M. P., and Soulsby, C.: What can we learn from multi-data calibration of a process-based ecohydrological model?, Environ. Model. Softw., 101, 301–316, 2018. a
Lees, T., Buechel, M., Anderson, B., Slater, L., Reece, S., Coxon, G., and Dadson, S. J.: Benchmarking data-driven rainfal–runoff models in Great Britain: a comparison of long short-term memory (LSTM)-based models with four lumped conceptual models, Hydrol. Earth Syst. Sci., 25, 5517–5534, https://doi.org/10.5194/hess-25-5517-2021, 2021. a, b
Legates, D. R. and McCabe Jr., G. J.: Evaluating the use of “goodness‐of‐fit” measures in hydrologic and hydroclimatic model validation, Water Resour. Res., 35, 233–241, 1999. a
Levine, S., Finn, C., Darrell, T., and Abbeel, P.: End-to-end training of deep visuomotor policies, J. Mach. Learn. Res., 17, 1334–1373, 2016. a
Li, B.: The code of hybrid hydrological models, Tsinghua University [code], https://cloud.tsinghua.edu.cn/d/1bb19608a7024abfaa3e/ (last access: 6 June 2024), 2024. a
Li, B., Zhou, X., Ni, G., Cao, X., Tian, F., and Sun, T.: A multi-factor integrated method of calculation unit delineation for hydrological modeling in large mountainous basins, J. Hydrol., 597, 126180, https://doi.org/10.1016/j.jhydrol.2021.126180, 2021. a
Li, B., Li, R., Sun, T., Gong, A., Tian, F., Khan, M. Y. A., and Ni, G.: Improving LSTM hydrological modeling with spatiotemporal deep learning and multi-task learning: a case study of three mountainous areas on the Tibetan Plateau, J. Hydrol., 620, 129401, https://doi.org/10.1016/j.jhydrol.2023.129401, 2023a. a, b, c, d, e
Li, B., Sun, T., Tian, F., and Ni, G.: Enhancing process-based hydrological models with embedded neural networks: A hybrid approach, J. Hydrol., 625, 130107, https://doi.org/10.1016/j.jhydrol.2023.130107, 2023b. a, b, c, d, e, f, g, h, i, j
Liu, Y., Zhang, T., Kang, A., Li, J., and Lei, X.: Research on Runoff Simulations Using Deep-Learning Methods, Sustainability, 13, 1336, https://doi.org/10.3390/su13031336, 2021. a
Lu, D., Konapala, G., Painter, S. L., Kao, S.-C., and Gangrade, S.: Streamflow simulation in data-scarce basins using Bayesian and physics-informed machine learning models, J. Hydrometeorol., 22, 1421–1438, https://doi.org/10.1175/JHM-D-20-0082.1, 2021. a
Myneni, R., Knyazikhin, Y., and Park, T.: MOD15A2H MODIS/Terra leaf area Index/FPAR 8-Day L4 global 500 m SIN grid V006, NASA EOSDIS Land Processes DAAC, NASA, https://doi.org/10.5067/MODIS/MYD15A2H.006, 2015. a
Nan, Y., He, Z., Tian, F., Wei, Z., and Tian, L.: Can we use precipitation isotope outputs of isotopic general circulation models to improve hydrological modeling in large mountainous catchments on the Tibetan Plateau?, Hydrol. Earth Syst. Sci., 25, 6151–6172, https://doi.org/10.5194/hess-25-6151-2021, 2021. a
Nash, J. and Sutcliffe, J.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, 1970. a
Nearing, G. S., Kratzert, F., Sampson, A. K., Pelissier, C. S., Klotz, D., Frame, J. M., Prieto, C., and Gupta, H. V.: What Role Does Hydrological Science Play in the Age of Machine Learning?, Water Resour. Res., 57, e2020WR028091, https://doi.org/10.1029/2020WR028091, 2021. a
Newman, A. J., Clark, M. P., Sampson, K., Wood, A., Hay, L. E., Bock, A., Viger, R. J., Blodgett, D., Brekke, L., Arnold, J. R., Hopson, T., and Duan, Q.: Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: data set characteristics and assessment of regional variability in hydrologic model performance, Hydrol. Earth Syst. Sci., 19, 209–223, https://doi.org/10.5194/hess-19-209-2015, 2015. a
Noël, P., Rousseau, A. N., Paniconi, C., and Nadeau, D. F.: Algorithm for delineating and extracting hillslopes and hillslope width functions from gridded elevation data, J. Hydrol. Eng., 19, 366–374, 2014. a
Nourani, V., Khodkar, K., and Gebremichael, M.: Uncertainty assessment of LSTM based groundwater level predictions, Hydrolog. Sci. J., 67, 773–790, 2022. a
Patil, S. and Stieglitz, M.: Modelling daily streamflow at ungauged catchments: what information is necessary?, Hydrol. Process., 28, 1159–1169, 2014. a, b, c, d
Patil, S. D. and Stieglitz, M.: Comparing spatial and temporal transferability of hydrological model parameters, J. Hydrol., 525, 409–417, 2015. a
Patil, S. D., Wigington Jr, P. J., Leibowitz, S. G., Sproles, E. A., and Comeleo, R. L.: How does spatial variability of climate affect catchment streamflow predictions?, J. Hydrol., 517, 135–145, 2014. a, b, c, d, e
Quilty, J. M., Sikorska-Senoner, A. E., and Hah, D.: A stochastic conceptual-data-driven approach for improved hydrological simulations, Environ. Model. Softw., 149, 105326, https://doi.org/10.1016/j.envsoft.2022.105326, 2022. a
Shen, C., Appling, A. P., Gentine, P., Bandai, T., Gupta, H., Tartakovsky, A., Baity-Jesi, M., Fenicia, F., Kifer, D., and Li, L.: Differentiable modelling to unify machine learning and physical models for geosciences, Nat. Rev. Earth Environ., 4, 552–567, https://doi.org/10.1038/s43017-023-00450-9, 2023. a, b, c
Solgi, R., Loaiciga, H. A., and Kram, M.: Long short-term memory neural network (LSTM-NN) for aquifer level time series forecasting using in-situ piezometric observations, J. Hydrol., 601, 126800, https://doi.org/10.1016/j.jhydrol.2021.126800, 2021. a
Su, T., Miao, C., Duan, Q., Gou, J., Guo, X., and Zhao, X.: Hydrological response to climate change and human activities in the Three-River Source Region, Hydrol. Earth Syst. Sci., 27, 1477–1492, https://doi.org/10.5194/hess-27-1477-2023, 2023. a, b, c
Tian, F., Hu, H., Lei, Z., and Sivapalan, M.: Extension of the Representative Elementary Watershed approach for cold regions via explicit treatment of energy related processes, Hydrol. Earth Syst. Sci., 10, 619–644, https://doi.org/10.5194/hess-10-619-2006, 2006. a
TPDC: China meteorological forcing dataset (1979–2018), TPDC [data set], https://doi.org/10.11888/AtmosphericPhysics.tpe.249369.file, 2024. a
Tsai, W. P., Feng, D., Pan, M., Beck, H., Lawson, K., Yang, Y., Liu, J., and Shen, C.: From calibration to parameter learning: Harnessing the scaling effects of big data in geoscientific modeling, Nat. Commun., 12, 5988, https://doi.org/10.1038/s41467-021-26107-z, 2021. a
USGS: MOD15A2H v006 MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500 m SIN Grid, USGS [data set], https://doi.org/10.5067/MODIS/MOD15A2H.006, 2024. a
van Pelt, S. C., Kabat, P., ter Maat, H. W., van den Hurk, B. J. J. M., and Weerts, A. H.: Discharge simulations performed with a hydrological model using bias corrected regional climate model input, Hydrol. Earth Syst. Sci., 13, 2387–2397, https://doi.org/10.5194/hess-13-2387-2009, 2009. a
Viviroli, D., Archer, D. R., Buytaert, W., Fowler, H. J., Greenwood, G. B., Hamlet, A. F., Huang, Y., Koboltschnig, G., Litaor, M. I., López-Moreno, J. I., Lorentz, S., Schädler, B., Schreier, H., Schwaiger, K., Vuille, M., and Woods, R.: Climate change and mountain water resources: overview and recommendations for research, management and policy, Hydrol. Earth Syst. Sci., 15, 471–504, https://doi.org/10.5194/hess-15-471-2011, 2011. a
Xie, K., Liu, P., Zhang, J., Han, D., Wang, G., and Shen, C.: Physics-guided deep learning for rainfall-runoff modeling by considering extreme events and monotonic relationships, J. Hydrol., 603, 127043, https://doi.org/10.1016/j.jhydrol.2021.127043, 2021. a, b
Xu, R., Hu, H., Tian, F., Li, C., and Khan, M. Y. A.: Projected climate change impacts on future streamflow of the Yarlung Tsangpo-Brahmaputra River, Global Planet. Change, 175, 144–159, 2019. a
Yang, K., He, J., Tang, W., Qin, J., and Cheng, C. C.: On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau, Agr. Forest Meteorol., 150, 38–46, 2010. a
Yilmaz, K. K., Gupta, H. V., and Wagener, T.: A process‐based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model, Water Resour. Res., 44, W09417, https://doi.org/10.1029/2007WR006716, 2008. a
Zhong, L., Lei, H., and Gao, B.: Developing a Physics‐Informed Deep Learning Model to Simulate Runoff Response to Climate Change in Alpine Catchments, Water Resour. Res., 59, e2022WR034118 , https://doi.org/10.1029/2022WR034118, 2023. a, b, c
- Abstract
- Introduction
- Methods and materials
- Model evaluation
- The applicability of hybrid models for hydrological sensitivities to climate change
- Conclusions and limitations
- Appendix A
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methods and materials
- Model evaluation
- The applicability of hybrid models for hydrological sensitivities to climate change
- Conclusions and limitations
- Appendix A
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Financial support
- Review statement
- References