Modeling groundwater responses to climate change in the Prairie Pothole Region

Shallow groundwater in the Prairie Pothole Region (PPR) is predominantly recharged by snowmelt in the spring and supplies water for evapotranspiration through the summer and fall. This two-way exchange is underrepresented in current land surface models. Furthermore, the impacts of climate change on the groundwater recharge rates are uncertain. In this paper, we use a coupled land–groundwater model to investigate the hydrological cycle of shallow groundwater in the PPR and study its response to climate change at the end of the 21st century. The results show that the model does a reasonably good job of simulating the timing of recharge. The mean water table depth (WTD) is well simulated, except for the fact that the model predicts a deep WTD in northwestern Alberta. The most significant change under future climate conditions occurs in the winter, when warmer temperatures change the rain/snow partitioning, delaying the time for snow accumulation/soil freezing while advancing early melting/thawing. Such changes lead to an earlier start to a longer recharge season but with lower recharge rates. Different signals are shown in the eastern and western PPR in the future summer, with reduced precipitation and drier soils in the east but little change in the west. The annual recharge increased by 25 % and 50 % in the eastern and western PPR, respectively. Additionally, we found that the mean and seasonal variation of the simulated WTD are sensitive to soil properties; thus, fine-scale soil information is needed to improve groundwater simulation on the regional scale.

1 Introduction

The Prairie Pothole Region (PPR) in North America is located in a semiarid and cold region, where evapotranspiration (ET) exceeds precipitation (PR) in summer and near-surface soil is frozen in winter (Gray, 1970; Granger and Gray, 1989; Hayashi et al., 2003; Pomeroy, 2007; Ireson et al., 2013; Dumanski et al., 2015). These climatic conditions have introduced unique hydrological characters to the groundwater flow in the PPR (Ireson et al., 2013). During winter, frozen soils reduce permeability and snow accumulates on the surface, prohibiting infiltration (Niu and Yang, 2006; Mohammed et al., 2018). At the same time, the water table slowly declines due to a combination of upward transport to the freezing front by the capillary effect and discharge to rivers (Ireson et al., 2013). In early spring, snowmelt becomes the dominant component of the hydrological cycle and the melt water runs over frozen soil, with little infiltration contributing to recharge. As the soil thaws, the increased infiltration capacity allows snowmelt recharge to the water table, the previously upward water movement due to the capillary effect to reverse and move downwards, and the water table to rise to its maximum level. In summer and fall, when high ET exceeds PR, capillary rise may draw water from the groundwater aquifers to supply ET demands, decreasing the water table. These processes characterize the critical two-way water exchange between the unsaturated soils and saturated groundwater aquifers.

Previous studies have suggested that substantial changes to groundwater interactions with unsaturated soils are likely to occur under climate change (Tremblay et al., 2011; Green et al., 2011; Ireson et al., 2013, 2015). Existing modeling studies on the impacts of climate change on groundwater are either at global or basin/location-specific scales (Meixner et al., 2016). Global-level groundwater studies focus on potential future recharge trends (Döll and Fiedler, 2008; Döll, 2009; Green et al., 2011), yet coarse-resolution analysis from global climate models (GCMs) provides insufficient specificity to inform decision making. Basin-scale groundwater studies connect the climate with groundwater-flow models in order to understand the climate impacts on specific systems (Maxwell and Kollet, 2008; Kurylyk and MacQuarrie, 2013; Dumanski et al., 2015). Regional groundwater modeling studies, such as in the Colorado River basin (Christensen et al., 2004) and in the western US (Niraula et al., 2017), have applied downscaled climate scenarios from GCMs to drive large-scale hydrology models. These studies identified research gaps associated with the poor representation of groundwater–soil interactions in models and uncertainties in future climate projections.

It is challenging to represent groundwater flows in LSMs (land surface models), as the important two-way water exchange between unsaturated soils and groundwater aquifers has been neglected in previous LSMs. Recently, this two-way exchange has been implemented in coupled land surface–groundwater models (LSM-GW). For example, Maxwell and Miller (2005) used a groundwater model (ParFlow) coupled with the Common Land Model (CLM) as a single-column model. They found that the coupled and uncoupled models were very similar with respect to simulated sensible heat flux (SH), ET, and shallow soil moisture (SM), but differed greatly in simulated runoff and deep SM. Later on, Kollet and Maxwell (2008) incorporated the ET effect on redistributing moisture upward from a shallow water table depth (WTD) and found that the surface energy partitioning is highly sensitive to the WTD when the WTD is less than 5 m b.g.s. (below ground surface). Niu et al. (2011) implemented a simple groundwater model (SIMGM, Niu et al., 2007), into the community Noah LSM with multi-parameterization options (Noah-MP LSM), by adding an unconfined aquifer at the bottom of the soil layers. More complex features such as three-dimensional subsurface flow and two-dimensional surface were included in ParFlow v3 and evaluated over much of continental North America for a very fine 1 km resolution (Maxwell et al., 2015). These recent developments in coupled land and groundwater models have advanced our knowledge on the important interactions between soil and groundwater aquifers.

In cold regions, soil freeze–thaw processes further complicate this two-way exchange. Field studies have found that frozen soil not only influences the timing and amount of downward recharge to aquifers by reducing the soil permeability (Koren et al., 1999; Niu and Yang, 2006; Kelln et al., 2007), but may also induce upward water transport from aquifers to soil freezing fronts (Spaans and Baker, 1996; Remenda et al., 1996; Hansson et al., 2004). In the modeling community, a range of approaches have been applied to deal with frozen soil parameterizations. Earlier LSMs assumed no significant heat transfer and soil water redistribution for subfreezing temperatures, for example, in simplified SiB and BATS (Xue et al., 1991; Dickinson et al., 1993; Niu and Zeng, 2012). Koren et al. (1999) suggested that the frozen soil is permeable due to macropores that exist in soil structural aggregates, such as cracks, dead root passages, and worm holes. The Noah v3 model adopted this scheme as its default option. Niu and Yang (2006) suggested separating a model grid into frozen and unfrozen patches, and that these two patches have a linear effect on the soil hydraulic properties. This treatment was incorporated into CLM 3.0 and Noah-MP in 2007 and 2011, respectively.

The spatial heterogeneity of soil moisture and WTD requires high-resolution meteorological input that direct outputs from GCMs are too coarse to provide. In GCMs, differences in simulated precipitation stem from the choice of the convection parameterization scheme (Sherwood et al., 2014; Prein et al., 2015). An important approach to improve precipitation simulation is to conduct dynamical downscaling using the convection-permitting model (CPM) (Ban et al., 2014; Prein et al., 2015; Liu et al., 2017). The CPM uses a high spatial resolution (usually under 5 km) to explicitly resolve convection without activating convection parameterization schemes. CPMs can also improve the representation of fine-scale topography and spatial variations of surface fields (Prein et al., 2013). These CPM added-values provide an excellent opportunity to investigate water table dynamics in the PPR.

The objectives of this paper are (1) to investigate the performance of a regional-scale coupled land–groundwater model in simulating groundwater water levels, recharge, and storage in a seasonally frozen environment in the PPR and (2) to explore the possible impacts of climate change on these processes.

In this paper, we use a physical process-based LSM (Noah-MP) coupled with a groundwater dynamics model (MMF model). The coupled Noah-MP-MMF model is driven by two sets of meteorological forcing for 13 years under current and future climate scenarios. These two sets of meteorological data are from a CPM dynamical downscaling project using the Weather Research and Forecasting (WRF) model with 4 km grid spacing covering the contiguous US and southern Canada (WRF CONUS, Liu et al., 2017). The paper is structured as follows: Sect. 2 introduces the groundwater observations for the WTD evaluation in the PPR, the coupled Noah-MP-MMF model, and the meteorological forcing from the WRF CONUS project. Section 3 evaluates the model simulated WTD time series and shows the groundwater budget and hydrological changes due to climate change. Sections 4 and 5 offer a broad discussion and conclusion.

Figure 1 (a) Topography (m) of the Prairie Pothole Region (PPR) and the station locations of groundwater wells (red dots); (b) topography (m) of the WRF CONUS domain, with the black box indicating the PPR domain.

2 Data and methods

2.1 Observational data

Groundwater observation data were obtained through several agencies: (1) the United States Geological Survey (USGS) National Water Information System in the US (https://waterdata.usgs.gov/nwis/gw, last access: September 2019); (2) the Alberta Environment and Parks (http://aep.alberta.ca/water/programs-and-services/groundwater/groundwater-observation-well-network/default.aspx, last access: September 2019); and (3) the Saskatchewan Water Security Agency (https://www.wsask.ca/Water-Info/Ground-Water/Observation-Wells/, last access: September 2019).

Initially, groundwater data from 160 wells were acquired, 72 wells in the US, 43 wells in Alberta, and 45 wells in Saskatchewan. We used the following criteria to select qualified stations for our study and evaluate our model performance against these observations:

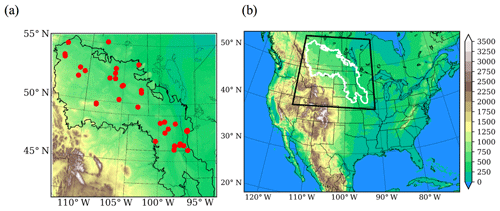
1. The locations of the wells are within the PPR region.

2. A sufficiently long data record exists during the simulation period. We define the observation availability as the available observation period within the 13-year simulation period and select wells with an observation availability greater than 80 %.

3. We only take data from unconfined aquifers with shallow groundwater levels (mean WTD > 5 m).

4. We only take data with minimal anthropogenic effects (such as from pumping or irrigation).

These criteria reduced the observation data to 33 well records, with 14 from the US, 6 in Alberta, and 13 in Saskatchewan. Table 1 summarizes the information for each selected well, and Fig. 1a shows the location of the wells in our study area. It is noteworthy that most of the groundwater sites have more permeable deposits (sand and gravel), as provincial and state agencies do not monitor low-permeability formations. More information about the selection criteria are provided in the Supplement.

Table 1 Summary of the locations, aquifer type, and soil type of the 33 selected wells.

2.2 Groundwater and frozen soil scheme in Noah-MP

In the present study, we used the community Noah-MP LSM (Niu et al., 2011; Yang et al., 2011) coupled with a GW model – the MMF model (Fan et al., 2007; Miguez-Macho et al., 2007). This coupled model has been applied in many regional hydrology studies in offline mode (Miguez-Macho and Fan, 2012; Martinez et al., 2016) and has also been coupled with regional climate models (Anyah et al., 2008; Barlage et al., 2015). Here, we present a brief introduction to the MMF groundwater scheme and the frozen soil scheme in Noah-MP; further details can be found in previous studies (Fan et al., 2007; Miguez-Macho et al., 2007; Niu and Yang, 2006).

Figure 2 is a diagram of the structure of four soil layers (0.1, 0.3, 0.6, and 1.0 m) and the underlying unconfined aquifer in Noah-MP-MMF. The MMF scheme explicitly defines an unconfined aquifer below the 2 m soil level and an auxiliary soil layer stretching to the WTD, which varies in space and time (m). The thickness of this auxiliary layer ,z_aux (m), is also variable, depending on the WTD:

$$\begin{array}{}\text{(1)}& z_{\mathrm{aux}}=\left\{\begin{array}{ll}\mathrm{1},& \mathrm{WTD}\ge -\mathrm{3}\\ -\mathrm{2}-\mathrm{WTD},& \mathrm{WTD}<-\mathrm{3}\end{array}\right..\end{array}$$

The vertical fluxes include gravity drainage and capillary flux, solved from the Richards' equation:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& q=K_{\mathit{\theta }}\left({\displaystyle \frac{\partial \mathit{\psi }}{\partial z}}-\mathrm{1}\right),K_{\mathit{\theta }}=K_{\mathrm{sat}}\cdot {\left({\displaystyle \frac{\mathit{\theta }}{{\mathit{\theta }}_{\mathrm{sat}}}}\right)}^{\mathrm{2}b+\mathrm{3}},\\ & \mathit{\psi }={\mathit{\psi }}_{\mathrm{sat}}\cdot {\left({\displaystyle \frac{{\mathit{\theta }}_{\mathrm{sat}}}{\mathit{\theta }}}\right)}^b.\end{array}\end{array}$$

Here, q is water flux between two adjacent layers (m s⁻¹), K_θ is the hydraulic conductivity (m s⁻¹) at a certain soil moisture content θ (m³ m⁻³), ψ is the soil matric potential (m), and b is soil pore size index. The subscript “sat” denotes saturation. The recharge flux from/to the layer above the WTD, R, can be obtained according to the WTD:

$$\begin{array}{}\text{(3)}& R=\left\{\begin{array}{ll}{K}_k\cdot \left(\frac{{\mathit{\psi }}_i-{\mathit{\psi }}_k}{z_{\mathrm{soil}\left(i\right)}-z_{\mathrm{soil}\left(k\right)}}-\mathrm{1}\right),& \mathrm{WTD}\ge -\mathrm{2}\\ K_{\mathrm{aux}}\cdot \left(\frac{{\mathit{\psi }}_{\mathrm{4}}-{\mathit{\psi }}_{\mathrm{aux}}}{(-\mathrm{2})-(-\mathrm{3})}-\mathrm{1}\right),& -\mathrm{2}>\mathrm{WTD}\ge -\mathrm{3}\\ K_{\mathrm{sat}}\cdot \left(\frac{{\mathit{\psi }}_{\mathrm{aux}}-{\mathit{\psi }}_{\mathrm{sat}}}{(-\mathrm{2})-\left(\mathrm{WTD}\right)}-\mathrm{1}\right),& \mathrm{WTD}<-\mathrm{3}\end{array}\right..\end{array}$$

In the first case, the WTD is in the resolved soil layers and z_soil is the depth of the soil layer with the subscript k indicating the layer containing WTD while i is the layer above. The calculated water table recharge is then passed to the MMF groundwater routine.

The change of groundwater storage in the unconfined aquifer considers three components: recharge flux (R), river discharge (Q_r), and lateral flows (Q_lat):

$$\begin{array}{}\text{(4)}& \mathrm{\Delta }{S}_{\mathrm{g}}=\left(R-Q_{\mathrm{r}}+\sum Q_{\mathrm{lat}}\right),\end{array}$$

where S_g (mm) is groundwater storage, Q_r (mm) is the water flux of groundwater–river exchange, and ∑Q_lat (mm) are groundwater lateral flows to/from all surrounding grid cells. The groundwater lateral flow (∑Q_lat) is the total horizontal flows between each grid cell and its neighboring grid cells, calculated from Darcy's law with the Dupuit–Forchheimer approximation (Fan and Miguez-Macho, 2010), as follows:

$$\begin{array}{}\text{(5)}& Q_{\mathrm{lat}}=wT\left({\displaystyle \frac{h-h_n}{l}}\right),\end{array}$$

where w is the width of the cell interface (m); T is the transmissivity of groundwater flow (m² s⁻¹); h and h_n are the water table head (m) of the local and neighboring cell, respectively; and l is the length (m) between cells. T depends on hydraulic conductivity K and the WTD:

$$\begin{array}{}\text{(6)}& T=\left\{\begin{array}{ll}{\int }_{-\mathrm{\infty }}^{h}K\mathrm{d}z& \mathrm{WTD}\ge -\mathrm{2}\\ {\int }_{-\mathrm{\infty }}^{\left(z_{\mathrm{surf}}-\mathrm{2}\right)}K\mathrm{d}z+\sum K_i\cdot \mathrm{d}{z}_i& \mathrm{WTD}<-\mathrm{2}\end{array}\right..\end{array}$$

For WTD < −2, K is assumed to decay exponentially with depth, $K=K_{\mathrm{4}}\exp (-z/f)$; K₄ is the hydraulic conductivity in the fourth soil layer; and f is the e-folding length and depends on terrain slope. For WTD ≥ −2, i represents the number of layers between the water table and the 2 m bottom, and z_surf is the surface elevation.

The river flux (Q_r) is also represented by a Darcy's law-type equation, where the flux depends on the gradient between the groundwater and the river depth and the riverbed conductance:

$$\begin{array}{}\text{(7)}& Q_{\mathrm{r}}=\mathrm{RC}\cdot \left(h-z_{\mathrm{river}}\right),\end{array}$$

where z_river is the depth of the river (m) and RC is dimensionless river conductance, which depends on the slope of the terrain and equilibrium water table. Equation (8) is a simplification that uses z_river rather than the water level in the river, and, for this study, we only consider one-way discharge from groundwater to rivers. Finally, the change in the WTD is calculated as the total fluxes that fill or drain the pore space between saturation and the equilibrium soil moisture state, θ_eq (m³ m⁻³), in the layer containing the WTD:

$$\begin{array}{}\text{(8)}& \mathrm{\Delta }\mathrm{WTD}={\displaystyle \frac{\mathrm{\Delta }{S}_{\mathrm{g}}}{\left({\mathit{\theta }}_{\mathrm{sat}}-{\mathit{\theta }}_{\mathrm{eq}}\right)}}.\end{array}$$

If ΔS_g is greater than the pore space in the current layer, the soil moisture content of current layer is saturated and the WTD rises to the layer above, updating the soil moisture content in the layer above as well. The opposite is true for negative ΔS_g, as the water table declines and soil moisture decreases.

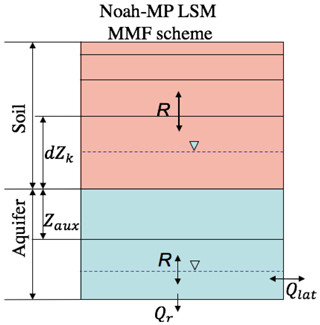
Figure 2 The structure of the Noah-MP LSM coupled with the MMF groundwater scheme showing the top 2 m of soil that is comprised of four layers with thicknesses of 0.1, 0.3, 0.6 and 1.0 m. An unconfined aquifer is added below the 2 m boundary, including an auxiliary layer and the saturated aquifer. A positive flux of R denotes downward transport. Two water tables are shown, one within the 2 m soil and the other below this level, indicating that the model is capable of dealing with both shallow and deep water tables.

There are two options in Noah-MP LSM for frozen soil permeability: option 1, the default option in Noah-MP, is from Niu and Yang (2006), and option 2 is inherited from the Koren et al. (1999) scheme from Noah v3. Option 1 assumes that a model grid cell consists of permeable and impermeable patches, and the area-weighted sum of these patches gives the grid cell soil hydraulic properties. Thus, the total soil moisture (θ) in the grid cell is used to compute hydraulic properties as follows:

$$\begin{array}{}\text{(9)}& \mathit{\theta }={\mathit{\theta }}_{\mathrm{ice}}+{\mathit{\theta }}_{\mathrm{liq}}\end{array}$$

$$\begin{array}{}\text{(10)}& K=\left(\mathrm{1}-F_{\mathrm{frz}}\right)K_{\mathrm{u}}=\left(\mathrm{1}-F_{\mathrm{frz}}\right)K_{\mathrm{sat}}{\left({\displaystyle \frac{\mathit{\theta }}{{\mathit{\theta }}_{\mathrm{sat}}}}\right)}^{\mathrm{2}b+\mathrm{3}},\end{array}$$

where the subscripts “frz” and “u” denote the frozen and unfrozen patches in the grid point, respectively. The impermeable frozen soil fraction is parameterized as follows:

$$\begin{array}{}\text{(11)}& F_{\mathrm{frz}}=e^{-\mathit{\alpha }\left(\mathrm{1}-{\mathit{\theta }}_{\mathrm{ice}}/{\mathit{\theta }}_{\mathrm{sat}}\right)}-e^{-\mathit{\alpha }},\end{array}$$

where α=3.0 is an adjustable parameter. The amount of liquid water in the soil layer is either θ_liq or θ_liq,max; the maximum amount of liquid water is calculated by a more general form of the freezing-point depression equation:

$$\begin{array}{}\text{(12)}& {\mathit{\theta }}_{\mathrm{liq},\max }={\mathit{\theta }}_{\mathrm{sat}}{\left\{{\displaystyle \frac{{\mathrm{10}}^{\mathrm{3}}{L}_{\mathrm{f}}\left(T_{\mathrm{soil}}-T_{\mathrm{frz}}\right)}{g{T}_{\mathrm{soil}}{\mathit{\psi }}_{\mathrm{sat}}}}\right\}}^{-\frac{\mathrm{1}}{b}},\end{array}$$

where T_soil and T_frz are soil temperature and freezing point (K), respectively; L_f is the latent heat of fusion (J kg⁻¹); and g is gravitational acceleration (m s⁻²).

In comparison, option 2 uses only the liquid water volume to calculate hydraulic properties and assumes a nonlinear effect of frozen soil on permeability. Moreover, option 2 uses a variant of the freezing-point depression equation with an extra term, (1+8θ_ice)², to account for the increased interface between soil particles and liquid water due to the increase of ice crystals. Generally, option 1 assumes that soil ice has a smaller effect on infiltration and simulates more permeable frozen soil than option 2 (Niu et al., 2011). For this reason, option 1 allows the soil water to move and redistribute more easily within the frozen soil, and we decide to use option 1 in our study.

Figure 3 Evaluation of the annual precipitation from WRF CONUS (a–d) and NARR (e–h) against rain gauge observations.

2.3 Forcing data

The output from the WRF CONUS dataset (Liu et al., 2017) is used as meteorological forcing to drive the Noah-MP-MMF model. The WRF CONUS project consists of two simulations. The first simulation is referred to as the current climate scenario, or control run (CTRL), runs from October 2000 to September 2013, and is forced with 6-hourly 0.7^∘ ERA-Interim reanalysis data. The second simulation is a perturbation to reflect the future climate scenario, closely following the pseudo-global warming (PGW) approach from previous works (Rasmussen et al., 2014). The PGW simulation is forced with 6-hourly ERA-Interim reanalysis data plus a delta climate change signal derived from an ensemble of CMIP5 models under the RCP8.5 emission scenario, and it reflects the climate change signal between the end of the 21st and 20th centuries.

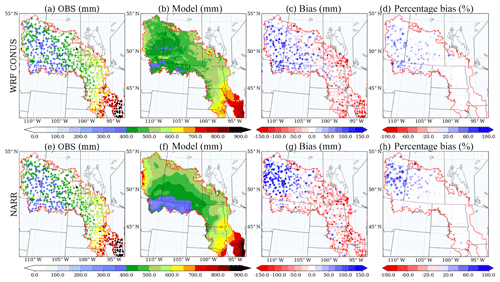
Figure 3 shows the annual precipitation in the PPR from 4 km WRF CONUS data from the current climate and 32 km North America Regional Reanalysis (NARR) data (NARR is another reanalysis dataset commonly used for land surface model forcing). Both datasets show similar annual precipitation patterns and bias patterns compared to observations: underestimating precipitation in the east and overestimating it in the west. However, WRF CONUS shows significant improvement of the percentage bias in precipitation, (model-observation)/observation, over the western PPR. For the consistency of the same source of data for current and future climate, WRF CONUS is the best available dataset for coupled land–groundwater study in the PPR.

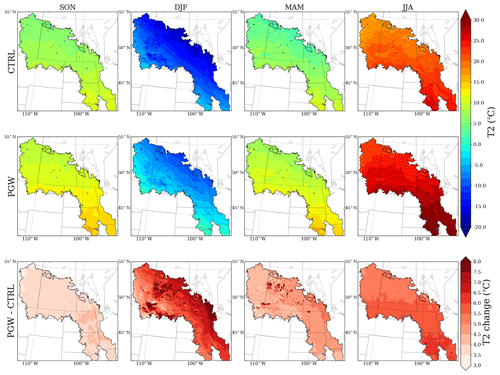
For the future climate study, the precipitation and temperature of the PGW climate forcing are shown in Figs. 4 and 5. WRF CONUS projects more precipitation in the PPR, except in the southeast of the domain in summer, where it shows a precipitation reduction of about 50–100 mm. In contrast, WRF CONUS projects that the strongest warming will occur in the northeastern PPR in winter (about 6–8 ^∘C as shown in Fig. 5). Another significant warming signal occurs in summer in the southeast of the domain, corresponding to the reduction of future precipitation, as seen in Fig. 4.

Figure 4 Seasonal accumulated precipitation from the current climate scenario (CTRL), the future climate scenario (PGW), and the projected change (PGW minus CTRL) in the forcing data.

Figure 5 Seasonal averaged temperature from CTRL, PGW, and the projected change (PGW minus CTRL).

2.4 Model setup

The two Noah-MP-MMF simulations representing the current climate and future climate are denoted as CTRL and PGW, respectively. The initial groundwater levels are from a global 1 km equilibrium groundwater map (Fan et al., 2013), and the equilibrium soil moisture for each soil layer is calculated at the first model time step with climatology recharge, spinning up for 500 years. As the model domain is at a different resolution to the input data, the appropriate initial WTD at 4 km may be different from the average at 1 km. To properly initialize the simulation, we spin the model up using the forcing of current climate (CTRL) for the years from 2000 to 2001 repeatedly (10 loops in total).

Due to different data sources, the default soil types along the boundary between the US and Canada are discontinuous. Thus, we use the global 1 km fine soil data (Shangguan et al., 2014, http://globalchange.bnu.edu.cn/research/soilw, last access: August 2019) in our study region. The soil properties for the aquifer use the same properties as the lowest soil layer from the Noah-MP 2 m soil layers.

3 Results

3.1 Comparison with groundwater observations

According to the locations of 33 groundwater wells in Table 1, the simulated WTD from the closest model grid points are extracted. Figure 6 shows the modeled WTD bias from the CTRL run. We also select the monthly WTD time series from eight sites, where the observation are denoted using black dots and the CTRL is shown using blue lines. The time series of the 33 sites are given in the Supplement. The model produces reasonable values of the mean WTD, and the mean bias is smaller than 1 m at most sites, except in Alberta, where the model predicts a deep bias of about 5 m in the northwestern part of the PPR. The model also successfully captures the annual cycle of the WTD, which rises in spring and early summer, because of snowmelt and rainfall recharge, and declines in summer and fall, because of high ET, and in winter, because of frozen near-surface soil. In all observations, the timing of the water table rising and dropping is well simulated, as the timing and amount of infiltration and recharge in spring is controlled by the freeze–thaw processes in seasonally frozen soil.

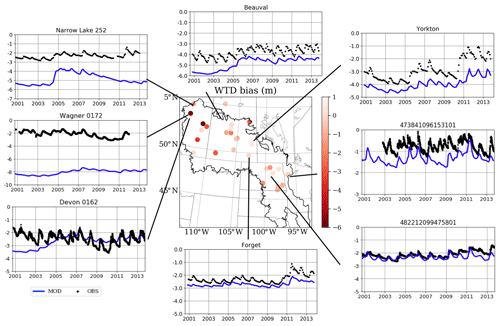
Figure 6 The WTD (m) bias from the CTRL simulation and time series from eight groundwater wells in the PPR (black denotes observations, and blue denotes the CTRL model simulation). See the “CTRL column” in Table 2 for the model statistics and the Supplement for complete time series from 33 wells.

In contrast, the model simulated WTD seasonal variation is smaller than observations. The small seasonal variation could be due to the misrepresentation between the lithology from the observational surveys and the soil types in the model grids. As mentioned in Sect. 2.2, the groundwater aquifer uses the same soil types as the bottom layer of the resolved 2 m soil layers. While sand and gravel are the dominant lithology at most of the sites, they are mostly clay and loam in the model (Table 1). For sandy soil reported at most of the sites, low capacity and fast responses to infiltration lead to large water table fluctuations, whereas, in the model, clay and loam soil allows low permeability and large capacity, and smoothens responses to recharge and capillary effects. Furthermore, the four-layer soils are vertically homogeneous with respect to soil type, and the groundwater model uses the lowest level soil type as the aquifer lithology. For many parts of the PPR, the groundwater levels are perched at the top 5 m below the surface due to a layer called glacial till. These geohydrological characteristics cannot be reflected in this model and contribute to the deep WTD bias simulated in Alberta. This shortcoming of the model was also reported in a study that took place in the Amazon rainforest (Miguez-Macho et al., 2012).

3.2 Climate change signal in groundwater fluxes

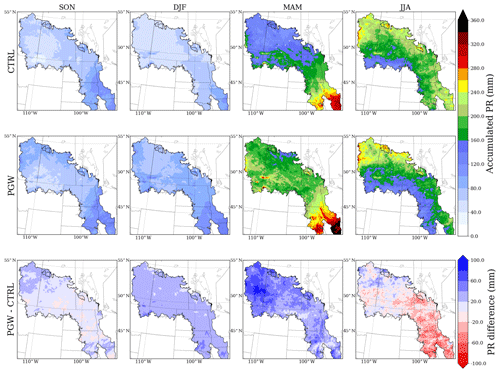
The MMF groundwater model simulates three components in the groundwater water budget: the recharge flux (R), lateral flow (Q_lat), and discharge flux to rivers (Q_r). Because the topography is usually flat in the PPR, the magnitude of groundwater lateral transport is very small (Q_lat less than 5 mm yr⁻¹). Conversely, the shallow water table in the PPR region is higher than the local river bed; thus, the Q_r term is always discharging from groundwater aquifers to rivers. As a result, the recharge term is the major contributor to the groundwater storage in the PPR, and its variation (usually between −100 and 100 mm) dominates the timing and amplitude of the water table dynamics. The seasonal accumulated total groundwater fluxes in the PPR ($R+Q_{\mathrm{lat}}-Q_{\mathrm{r}}$) are shown in Fig. 7. The positive (negative) flux shown in blue (red) means that the groundwater aquifer is gaining (losing) water, causing the water table to rise (decline).

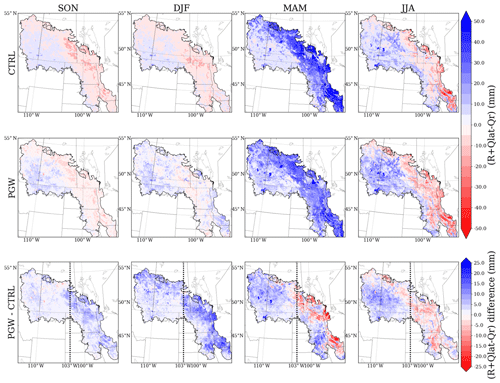
Figure 7 Seasonal accumulated total groundwater fluxes (R+) for the current climate (CTRL, top row), future climate (PGW, middle row), and projected change (PGW minus CTRL, bottom row) in the forcing data. Black dashed lines in PGW minus CTRL separate the PPR into eastern and western halves.

Under current climate conditions, the total groundwater fluxes show strong seasonal fluctuations, consistent with the WTD time series shown in Fig. 6. On average, in fall (SON) and winter (DJF), there is a 20 mm negative recharge, driven by the capillary effect that draws water from the aquifer to the dry soil above. Spring (MAM) is usually the season with a strong positive recharge because snowmelt provides a significant amount of water, and soil thawing allows infiltration. The large amount of snowmelt water contributes to more than 100 mm of positive recharge in the eastern domain. This occurs until summer (JJA), when strong ET depletes soil moisture and results in about 50 mm of negative recharge.

Under future climate conditions, the increased PR in fall and winter leads to wetter upper soil layers, resulting in a net positive recharge flux (PGW minus CTRL in SON and DJF). However, the PGW summer is impacted by increased ET under a warmer and drier climate, due to higher temperature and less PR. As a result, the groundwater uptake due to the capillary effect is more critical in the future summer. Furthermore, there is a strong east-to-west difference in the total groundwater flux change from PGW to CTRL. In the eastern PPR, the change in the total groundwater flux exhibits obvious seasonality, whereas the model projects persistent positive groundwater fluxes in the western PPR.

3.3 Water budget analysis

Figures 8 and 9 show the water budget analysis for the eastern and western PPR (divided by the dotted line at 103^∘ W in Fig. 7), respectively. Four components are presented in the figures: (1) PR and ET, (2) surface and underground runoff (SFCRUN and UDGRUN) and surface snowpack, (3) the change of soil moisture storage, and (4) groundwater fluxes and the change of storage. In the current and future climate, these budget terms are plotted as annual accumulation – columns (a) and (b) for CTRL and PGW, respectively – whereas their difference is plotted for each individual month – column (c) for PGW minus CTRL.

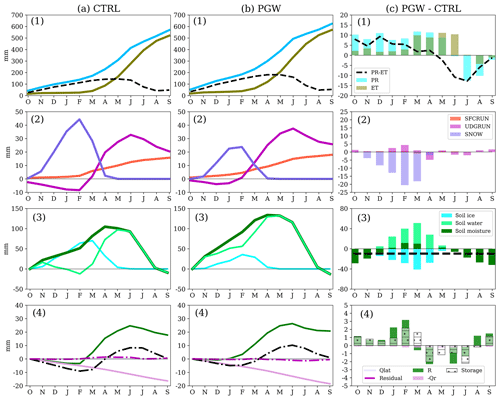
Figure 8 Water budget analysis in the eastern PPR in (a) CTRL, (b) PGW, and (c) PGW minus CTRL. Water budget terms include (1) PR and ET; (2) surface snow, surface runoff, and underground runoff (SNOW, SFCRUN, and UDGRUN); (3) change in soil moisture storage (soil water, soil ice, and total soil moisture, ΔSMC); and (4) groundwater fluxes and the change in groundwater storage (R, Q_lat, Q_r, ΔS_g). The annual mean soil moisture change (PGW minus CTRL) is shown using the black dashed line in (3). The residual term is defined as Res = (R+Q_lat-Q_r)−ΔS_g in (4). Note that in columns (a) and (b) the accumulated fluxes and change in storage are shown using lines, whereas in column (c) the difference in PGW minus CTRL is shown for each individual month using bars.

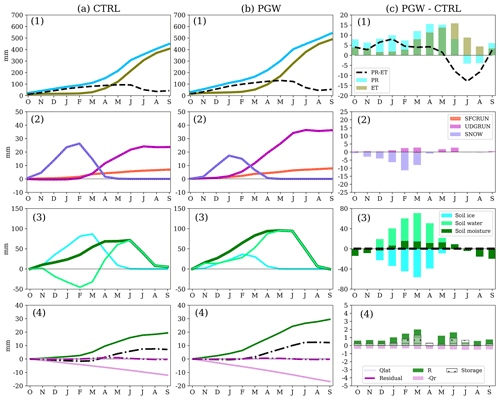
Figure 9 Same as Fig. 8 but for the western PPR. Water budget terms include (1) PR and ET; (2) surface snow, surface runoff, and underground runoff (SNOW, SFCRUN, and UDGRUN); (3) change of soil moisture storage (soil water, soil ice, and total soil moisture, ΔSMC); and (4) groundwater fluxes and the change of groundwater storage (R, Q_lat, Q_r, ΔS_g). The annual mean soil moisture change (PGW minus CTRL) is shown using a black dashed line in (3). The residual term is defined as Res = (R+Q_lat-Q_r)−ΔS_g in (4). Note that in columns (a) and (b) the accumulated fluxes and change in storage are shown using lines, whereas in column (c) the difference in PGW minus CTRL is shown for each individual month using bars.

Under current climate conditions, during snowmelt infiltration and rainfall events, water infiltrates into the top soil layer, travels through the soil column, and exits the bottom of the 2 m boundary; hence, the water table rises. During the summer dry season, ET is higher than PR and the soil layers lose water via ET; therefore, the capillary effect takes water from the underlying aquifer and the water table declines. In winter, the near-surface soil in the PPR is seasonally frozen; thus, a redistribution of subsurface water to the freezing front results in negative recharge, and the water table declines.

In the eastern PPR, the effective precipitation (PR-ET) is found to increase from fall to spring, but decrease in summer in PGW (Fig. 8c1). Warmer falls and winters in PGW, as well as increased PR, not only delay snow accumulation and bring forward snowmelt, but also change the precipitation partition – more precipitation occurs as rain and less as snow. This warming causes up to 20 mm of snowpack loss (Fig. 8c2). The underground runoff starts much earlier in PGW (December; Fig. 8b2) than in the CTRL (February; Fig. 8a2). Moreover, the warming in PGW also changes the partitioning of soil ice and soil water in unsaturated soil layers (Fig. 8c3). For late spring in PGW, the springtime recharge in the future is significantly reduced due to early melting and less snowpack remaining (Fig. 8c4). In the PGW summer, reduced PR (50 mm less) and higher temperatures (8 ^∘C warmer) lead to a reduction in total soil moisture and a stronger negative recharge from the aquifer. Therefore, the increase in recharge from fall to early spring compensates for the recharge reduction due to stronger ET in summer in the eastern PPR, and changes little in the annual mean groundwater storage (1.763 mm yr⁻¹).

These changes in water budget components in the western PPR (Fig. 9) are similar to those in the eastern PPR (Fig. 8), except in summer. The reduction in summer PR in the western the PPR (less than 5 mm reduction) is not as obvious as that in the eastern PPR (50 mm reduction) (Fig. 4). Thus, annual mean total soil moisture in the future is about the same as in the current climate (Fig. 9c3) and results in little negative recharge in PGW summer (Fig. 9c4). Therefore, the increase in annual recharge is more significant (10 mm  yr⁻¹), with an increase of about 50 % of the annual recharge in the current climate (20 mm yr⁻¹) (Fig. 9c4).

For both the eastern and western PPR, the water budget components for the groundwater aquifer are plotted in panel (4) in Figs. 8 and 9. The groundwater lateral flow is a small term in the areal average and has little impact on the groundwater storage. Nearly half of the increased recharge in both the eastern and western PPR is discharged to river flux (Q_r=2.26 mm from R=4.15 mm in the eastern PPR and Q_r=5.20 mm from R=10.72 mm in western PPR). Therefore, the groundwater storage change in the eastern PPR (1.76 mm yr⁻¹) is not as great as that in the western PPR (5.39 mm y r⁻¹).

These two regions of the PPR show differences in the hydrological response to future climate because of the spatial variation of the summer PR. As shown in both Fig. 4 (PGW minus CTRL) and panel (1) in Figs. 8 and 9, the reduction of future PR in summer in the eastern PPR is significant (50 mm). The spatial difference of precipitation changes in the PPR further results in the recharge increase doubling in the western PPR compared with the eastern PPR.

4 Discussion

4.1 Improving the WTD simulation

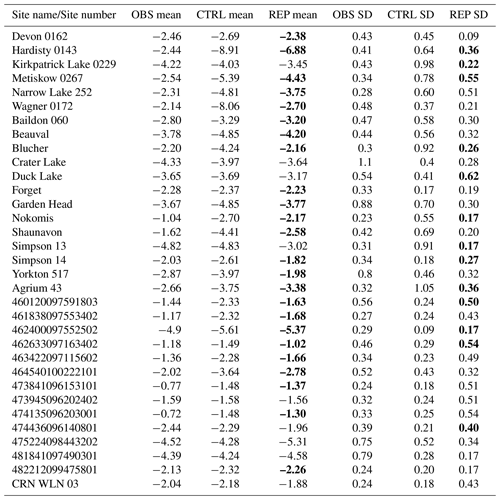
In Sect. 3.1, we show that the model is capable of simulating the mean WTD at most sites, although it predicts deep groundwater in Alberta and underestimates its seasonal variation. These results may be due to misrepresentations between the model default soil type and the soil properties in the observational wells. To test this theory, an additional simulation (REP) is conducted by replacing the default soil types in the locations of these 33 groundwater wells with sand-type soil, which is the dominant soil type reported from observational surveys. The time series of the REP and default CTRL simulations are shown in Fig. 10 (also see the supplemental materials for the complete 33 sites), and summaries of the mean and standard deviation of the two simulations are provided in Table 2.

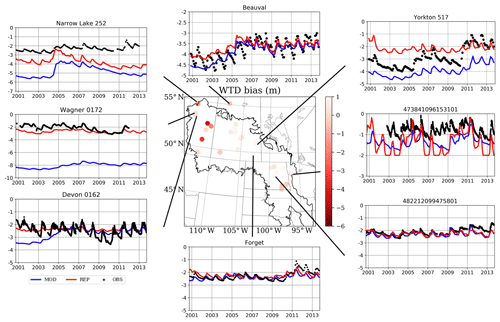
Figure 10 Same as Fig. 6 but the default soil type is replaced with sand-type soil in the model. WTD (m) bias from the CTRL simulation and time series from eight groundwater wells in the PPR (black denotes observations, blue denotes the CTRL model simulation, and red denotes simulations in which the soil type was replaced). The additional simulation (replacing the default soil type in the model with sandy soil type) is referred to as REP.

Table 2 Summary of mean and standard deviation (SD) of the WTD of 33 groundwater wells from the observation records (OBS), the default model (CTRL), and the additional simulation that replaces the default soil type with sand-type soil (REP). Bold text indicates an improvement in the REP simulation over the CTRL run.

The REP simulation with sandy soil shows two sensitive signals: (1) REP WTD values are shallower than the default simulation, and (2) they exhibit stronger seasonal variation. These two signals can be explained by the WTD equation in the MMF scheme:

$$\begin{array}{}\text{(13)}& \mathrm{\Delta }\mathrm{WTD}={\displaystyle \frac{\mathrm{\Delta }\left(R+Q_{\mathrm{lat}}-Q_{\mathrm{r}}\right)}{\left({\mathit{\theta }}_{\mathrm{sat}}-{\mathit{\theta }}_{\mathrm{eq}}\right)}}.\left(\mathrm{14}\right)\end{array}$$

Equation (14) represents that the change in the WTD over a period of time is calculated by the total groundwater fluxes, $\mathrm{\Delta }(R+Q_{\mathrm{lat}}-Q_{\mathrm{r}})$, divided by the available soil moisture capacity of the current layer (θ_sat−θ_eq). In the REP simulation, the parameter θ_sat for the dominant soil type at observational sites (sand/gravel) is smaller than those in default model grids (clay loam, sandy loam, loam, loamy sand, etc.). Therefore, changing the θ_sat is essentially reducing the storage in the aquifer and soil in this model grid. Given the same groundwater flux value, in the REP simulation, the mean WTD is higher and the seasonal variation is stronger than in the default CTRL run.

In the REP simulation, we only replaced the soil type at a limited number of sites because high-resolution geological survey data over a large area extent are not yet available for the entire PPR. At the point scale, the WTD responses to climate change over these limited number of sites show diverse results and uncertainties (see the Supplement). For the rest of the domain, the default soil type from a global 1 km soil map is used. The REP modifications of soil types at the point scale have a small contribution to the water balance analysis (Figs. 8, 9) at the regional scale. Our results and conclusions for the groundwater response to PGW does not change. We are currently undertaking a soil property survey project in the PPR region to obtain soil properties at a high spatial resolution, in both the horizontal and vertical directions. This may provide a better opportunity to improve WTD simulation as well as to assess the climate–groundwater interaction in future studies.

4.2 Climate change impacts on the groundwater hydrological regime

The warming and increased precipitation in cold seasons in future climate lead to later snow accumulation, higher recharge in winter, and earlier melting in spring compared with current climate.

Such changes in snowpack loss have been hypothesized in mountainous as well as high-latitude regions (Taylor et al., 2013; Ireson et al., 2015; Meixner et al., 2016; Musselman et al., 2017). In addition to the amount of recharge, the shift of recharge season is also noteworthy. Under current climate conditions in spring, soil thawing (in March) is generally later than snowmelt (in February) by a month in the PPR. Thus, the snowmelt water in pre-thaw spring would either refreeze after infiltrating into partially frozen soil or become surface runoff. Under the PGW climate, the warmer winter and spring allow snowmelt and soil thaw to occur earlier in the middle of winter (in January and February, respectively). As a result, the recharge season starts earlier (in December) and lasts longer (until June), resulting in a longer recharge season but with a lower recharge rate.

Future projected increasing evapotranspiration demand in summer desiccates soil moisture, resulting in more water uptake from aquifers to subsidize dry soil in the future summer. This groundwater transport to soil moisture is similar to the “buffer effect” documented in an offline study in the Amazon rainforest (Pokhrel et al., 2014). In the PPR, shallow water tables exist in the critical zone, where the WTD ranges from 1 to 5 m below the surface and could exert strong influence on land energy and moisture flux feedbacks to the atmosphere (Kollet and Maxwell, 2008; Fan, 2015). Previous coupled atmosphere–land–groundwater studies at a 30 km resolution showed that groundwater could support soil moisture during the summer dry period, but has little impact on precipitation in the central US (Barlage et al., 2015). It would be interesting to study the integrated impacts of shallow groundwater on regional climate in the convection-permitting resolution (resolution  < 5 km).

4.3 Fine-scale interaction between groundwater and pothole wetlands in the PPR

Furthermore, groundwater exchange with wetlands are complicated and critical in the PPR. Numerous wetlands known as potholes or sloughs are responsible for important ecosystem services, such as providing wildlife habitats and groundwater recharge (Johnson et al., 2010). Shallow groundwater aquifers may receive water from or lose water to prairie wetlands depending on the hydrological setting. Depression-focused recharge generated by runoff from uplands to depressions contributes to a sufficient amount of water input to shallow groundwater (5–40 mm yr⁻¹) (Hayashi et al., 2016).

Conversely, groundwater lateral flow exchange from the center of a wetland pond to its moist margin is also an important component in the wetland water balance (Van Der Kamp and Hayashi, 2009; Brannen et al., 2015; Hayashi et al., 2016). However, this groundwater–wetland exchange typically occurs on a local scale (from 10 to 100 m); thus, it is challenging to represent in current land surface models or climate models (resolution from 1 to 100 km). In this paper, we focus on the groundwater dynamics on the regional scale, which is still unable to capture these small wetland features in this study. We admit this limitation and are currently developing a sub-grid scheme to represent small-scale open water wetlands as a fraction within a grid cell and calculate their feedback to regional environments. Future studies on this topic will provide valuable insights into these key ecosystems and their interaction under climate change.

5 Conclusion

In this study, a coupled land–groundwater model is applied to simulate the interaction between the groundwater aquifer and soil moisture in the PPR. The climate forcing is from a dynamical downscaling project (WRF CONUS), which uses the convection-permitting model (CPM) configuration in high resolution. The goal of this study is to investigate the groundwater responses to climate change and to identify the major processes that contribute to these responses in the PPR. To our knowledge, this is the first study applying CPM forcing in a hydrology study in this region. We have three main findings:

1. The coupled land–groundwater model shows reliable simulation of mean WTD, although it underestimates the seasonal variation of the water table against well observations. This could be attributed to several reasons, including the misrepresentation of topography and soil types as well as the vertical homogenous soil layers used in the model. We further conducted an additional simulation (REP), in which we replace the model default soil types with sand-type soil, and the simulated WTDs were improved with respect to both the mean and seasonal variation. However, the inadequacy of soil properties in the deeper layer and higher spatial resolution is still a limitation.

2. Recharge markedly increases due to projected increased PR, particularly from fall to spring under future climate conditions. Strong east–west spatial variation exists in the annual recharge increases, with 25 % in the eastern and 50 % in the western PPR. This is due to the significant projected PR reduction in PGW summer in the eastern PPR but little change in the western PPR. This PR reduction leads to stronger ET demand, which draws more groundwater uptake due to the capillary effect, resulting in negative recharge in the summer. Therefore, the increased recharge from fall to spring is consumed by ET in summer and results in little change in groundwater in the eastern PPR, while water is gained in the western PPR.

3. The timing of infiltration and recharge are critically impacted by the changes in freeze–thaw processes. Increased precipitation, combined with higher winter temperatures, results in later snow accumulation/soil freezing, which is partitioned more as rain than snow, and earlier snowmelt/soil thaw. This leads to a substantial loss of snowpack, a shorter frozen soil season, and higher permeability in soil that allows infiltration. Late accumulation/freezing and early melting/thawing leads to an early start of a longer recharge season from December to June, although with a lower recharge rate.

Our study has some limitations, and future studies in these areas are encouraged:

1. Despite the large number of groundwater wells in PPR, only a few are suitable for long-term evaluation, due to data quality, anthropogenic pumping, and the length of the data record. As remote sensing techniques advance, observing terrestrial water storage anomalies derived from the GRACE satellite may provide substantial information on the WTD, although the GRACE information needs to be downscaled to a finer scale before comparisons can be made with regional hydrology models at the kilometer scale (Pokhrel et al., 2013).

2. This study is an offline study of climate change impacts on groundwater. It is important to investigate how shallow groundwater in the Earth's critical zone could interact with surface water and energy exchange to the atmosphere and affect regional climate. This investigation would be important to the central North American region (one of the land atmosphere coupling “hot spots”, Koster et al., 2004).